基于CSA算法的光伏阵列多峰最大功率跟踪研究

马永翔，王雨阳，闫群民，周建华，周玉龙

(1.陕西理工大学电气工程学院，陕西 汉中 723001；2.国网庆阳供电公司，甘肃 庆阳 745000)

太阳能作为绿色洁净、分布广泛的可再生能源，具有很强的开发应用前景。光伏发电系统中光伏电池的输出特性易受光照强度和温度变化的影响，因此必须通过光伏发电系统MPPT技术实现对其输出功率的最大功率点跟踪。传统的恒电压法和扰动观测法[2]等控制策略易陷入局部最优的陷阱，错失真正的最大功率点(MPP)，导致功率损失。因此为了保证系统的最大功率输出，必须要对MPPT技术加以改进。虽然目前大多数光伏电站都建在野外，很少会出现建筑物遮挡光照的情况，但因为其占地很广，不同光伏组件所处的实际工作环境也各有差别，例如受到云层或灰尘遮挡导致受到辐照度不同，还有因受到遮挡、高度落差产生的温度差别。这些环境参数上的差别以及光伏组件的老化等原因都会造成光伏组件的P-V输出功率曲线呈现多个峰值的状态。在各种影响PV输出的环境条件中，局部阴影(partial shading condition,PSC)是最为常见的。这种条件下恒电压控制法、扰动观测法(爬山法)和电导增量法[1-2]等这类传统MPPT控制策略会陷入局部最优点，导致功率损失。因此为了保证系统的最大功率输出，减少光伏系统调度的复杂性，必须要对MPPT技术加以改进。

关于随机环境情况下的MPPT，许多学者进行了研究，目前主流方法是将群体智能算法加入到MPPT中。文献[3]采用蚁群算法优化的RBF神经网络进行MPPT，经过验证其方法可以提升寻优精度，但其寻优结构较为复杂，难以实际应用。文献[4]使用蒙特卡洛算法，将MPPT问题转化为一种概率统计问题，可以有效追踪MPP，但其需要对大量的随机变量进行存储和计算，计算成本较大。文献[5]提出自适应权重的粒子群算法，改进传统的粒子群算法容易陷入局部最优解的缺点，提高了寻优速度与精度。文献[6]提出粒子群算法结合基于模糊控制电导增量法的混合控制策略，联合控制能进一步提高算法的寻优精度和控制效率。

布谷鸟搜索算法(cuckoo search algorithm,CSA)是一种新兴的智能优化算法，其具有参数少、实现简单等优点[7-9]。本文提出了一种根据布谷鸟搜索算法和传统的扰动观察法通过时序结合进行控制的MPPT方法，从工程控制论出发，直接采用Ump进行控制，并将其应用于MPPT中。通过MATLAB/Simulink仿真验证，该方法在随机环境下可精确地追踪到全局最大功率点。

1 通用条件下的光伏组件建模

1.1 光伏组件工程模型

在进行光伏组件相关理论分析的过程中，一般采用基于物理特性所建立的输出方程，其中的大多数参数不能准确测量。在实际光伏发电的过程中，光伏组件的运行控制需要标准测试条件(standard test condition,STC)，温度25℃，辐照度1 kW/m2下得到的MPP处电流和电压Im、Um，开路电压Uoc，短路电流Isc四个参数。为了让本文的仿真结果更加贴合实际应用的效果，采用如下光伏工程用模型[10]，输出特性表达式如式(1)：

式中：I和U为光伏组件的工作电流和电压。

传递变量C1、C2表达如式(2)：

在实际运行过程中，光伏组件的输出会受到辐照度和温度变化的影响发生改变，在变化的环境下光伏组件的四个参数可根据式(3)推算：

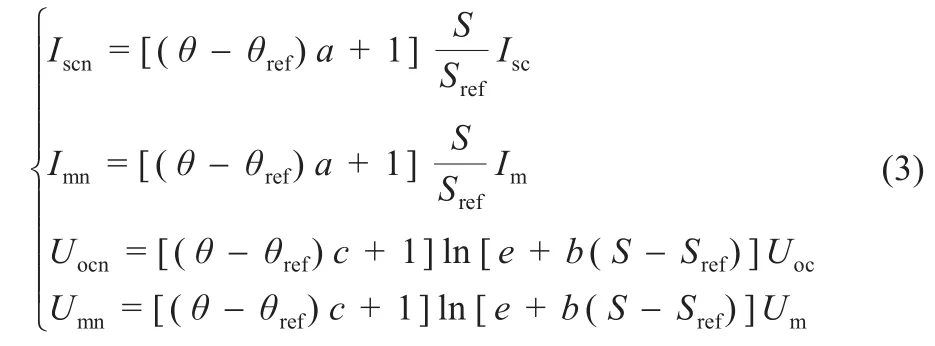
式中：Imn，Umn，Iscn，Uocn为在光伏组件所处环境的辐照度和温度条件变化时与之对应的系数；S,θ为实际工况下辐照度和温度；Sref和θref分别是辐照度和温度在STC下参考值；a、b、c为补偿系数，本文仿真中取典型值a=0.002 5 ℃－1，b=0.5(W/m2)－1，c=-0.002 8℃－1。通过上述3式即可得到任意环境工况下的光伏组件特性。

1.2 光伏组件输出特性

将光伏组件的工程用模型在MATLAB/Simulink中建立，并设置大范围变化的辐照度和温度，观察光伏组件输出电压、电流和功率的变化规律，其中光伏组件各参数取值为：Isc为8.63 A，Im为8.15 A，Uoc为37.4 V，Um为30.7 V。

在变环境条件下单体光伏组件的输出特性曲线如图1所示。

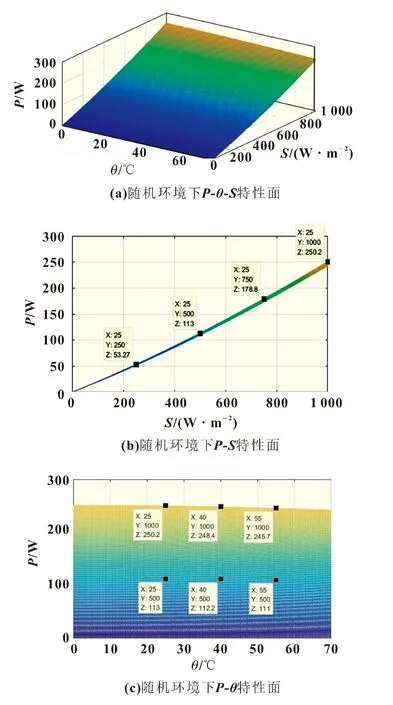
图1 单体光伏组件输出功率与环境参数θ和S之间关系

由图1可知，随着环境参数温度在0～70℃和辐照度在0～1 000 W/m2间变化，光伏组件的最大输出功率输出特性面是曲面。其中图1(b)是其主视图，着重体现了辐照度变换对MPP点的影响，可以看出随着辐照度下降，MPP也剧烈下降，在800～1 000 W/m2下降最明显。由式(3)可知，辐照度的变化对Umn影响较大，对Imn的影响极为明显，在25℃不变，辐照度从1 000 W/m2降低到500 W/m2的情况下，Umn下降2.96 V，Imn降低50%，下降了4.075 A，功率急剧下降137.2 W。图1(c)为左视图，可以明显看出其中温度变化对MPP影响较小，温度变化15℃，MPP变化只有2 W。由式(3)可知在辐照度1 000 W/m2不变，温度从15℃变换到35℃，Umn下降了1.76 V，Imn只上升了0.39 A，两者变化引起的功率变化只有2 W，所以温度对输出功率影响几乎可以忽略，但是温度对MPP处的Umn影响较大。对于根据需要检测Umn变化来进行MPPT的控制方法，关注温度变化极为重要。随着温度和辐照度的改变，光伏阵列的最大功率点的变化并不是线性变化，而是一种非线性的变化。

2 CSA和P&O协同控制分析

2.1 布谷鸟搜索算法

CSA是根据布谷鸟寻巢孵蛋行为产生的启发式算法。布谷鸟每次将自身的一枚蛋随机产在其他宿主鸟的巢中，最好的蛋会被孵化产生后代，而宿主鸟有Pa的概率会发现这枚外来的蛋，会将整个巢或该枚蛋抛弃。布谷鸟每次选择新巢的行为通过式(4)实现：

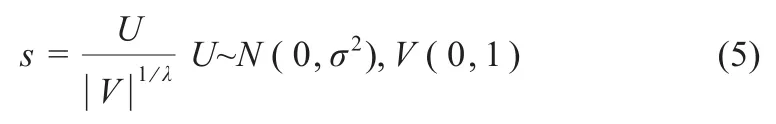
式中的代表样本服从均值为0，方差为σ2的高斯正态分布，方差可以使用式(6)计算：

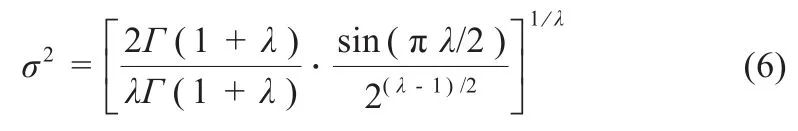
布谷鸟搜索算法，其本质与没有个体历史最优的粒子群算法(particle swarm optimization,PSO)相似，主更新公式与差分进化算法(differential evolution,DE)近似，在切换概率Pa的设置上则与模拟退火算法(simulated annealing,SA)相同。可以说CSA将粒子群算法、模拟退火算法、差分进化算法的优点结合在一起，是一种高效的寻优算法。

前列腺癌根治手术，因为需要进行膀胱颈和尿道的吻合，术后需要常规留置导尿管。尿管保留时间可由术者根据术中情况自行决定。目前，国内的中心术后尿管保留时间多为2～3周，但国外许多中心行腹腔镜前列腺癌根治手术后6～8 d即可拔除尿管，并未增加尿道吻合口并发症[10]。

2.2 基于布谷鸟搜索算法和爬山法的MPPT

本文提出一种将CSA和爬山法相结合的控制方法。CSA在大致寻到全局最优解附近时，在进行局部搜索的过程中，Levy飞行产生的随机步长若是较长会影响搜索精度，步长若是较短则会影响搜索速度。因此在迭代后期加入爬山法，通过施加不同方向的扰动，判断功率变化来进行局部精确锁定全局最大功率点。

其具体MPPT步骤如下：

步骤一：CSA初始化n个鸟巢，将不同的电压值当做巢的位置，巢的质量通过对应的功率体现。

步骤二：设定布谷鸟蛋被宿主鸟发现的概率Pa，并根据式(4)(5)(6)进行第一次Levy飞行。

步骤三：评价巢的质量，以贪婪法则保留较好的巢，

通过式(7)比较产生一个最优巢记为xbest。

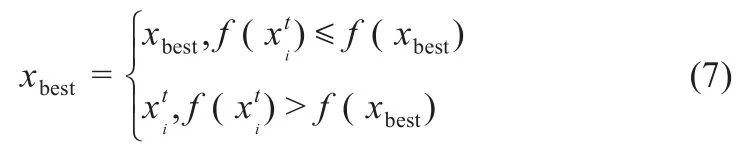
步骤四：以Pa概率抛弃一定量的巢，通过偏好随机游动，即式(8)生成等量新解。

步骤五：评价巢的质量，判断是否达成全局搜索条件，若否则返回步骤二继续进行迭代。

步骤六：在搜索到最大功率点附近后，对其施加小步长双向扰动，并对其进行比较。

步骤七：判断是否达成终止条件，未达成重复步骤六，达成输出最优解。

将布谷鸟搜索算法和爬山法进行协同控制，可以提升寻优的速度和精度。图2所示为最大功率跟踪结构图。

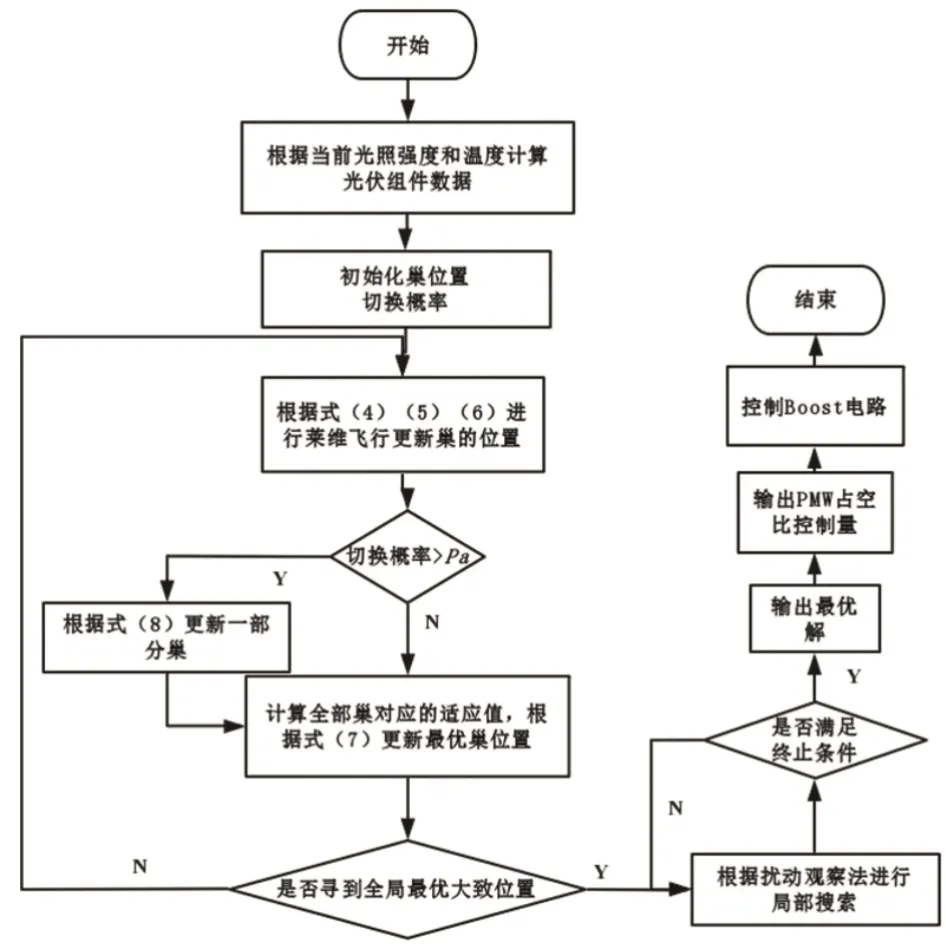
图2 最大功率跟踪结构图

3 仿真验证及结果分析

为了验证布谷鸟算法和爬山法相结合的算法在随机环境下应用于光伏阵列MPPT方法的有效性，在MATLAB/Simulink中搭建光伏阵列仿真模型。仿真模型含光伏组件、布谷鸟搜索算法和爬山法相结合的MPPT控制器、Boost变换器和负载，如图 3所示。图中C1取 50 μF，C2取200 μF，L取 5 mH，R取50 Ω，系统的采样周期为20 ms，Boost电路的开关频率取50 kHz。

图3 实验电路

将布谷鸟搜索算法和爬山法协同控制MPPT策略在不同环境条件下进行验证，与传统粒子群算法和爬山法比较，三者采用同样的电路参数进行仿真。设置CSA算法迭代次数为10，寻优粒子数目为30，发现概率Pa为0.25。

3.1 变环境参数光伏组件输出特性仿真

在实际工程应用中，大量的光伏组件进行串并联后接入逆变器，但是光伏板本身表面积较大，组合起来后往往占地很广。这样就很容易受到云、树木或建筑物等的遮挡，同一串组件就会受到不同光照强度和温度影响，从而产生多峰值的功率特性曲线。光伏电池组件采用四个组件串联形式，模拟光伏组件所处环境的多样性，现在假设出四种环境状态，如表1所示。

表1 四种环境参数表

随着温度和光照强度的改变，光伏阵列的最大功率点会随之改变。因考虑到实际工况下，不同光伏组件受到的辐照度会因为建筑等遮挡有较明显的变化，设置PSC1为四个光伏组件的辐照度逐渐递减100 W/m2，但在一定范围内温度的变化并不会太大，四个光伏组件的温差为3℃，是最贴合实际工况中可能出现的；PSC2则着重体现了大温差下的不同组件总的输出特性；PSC3则是随机设置了两两相同的状况。通过仿真得到的P-V特性曲线如图4所示。

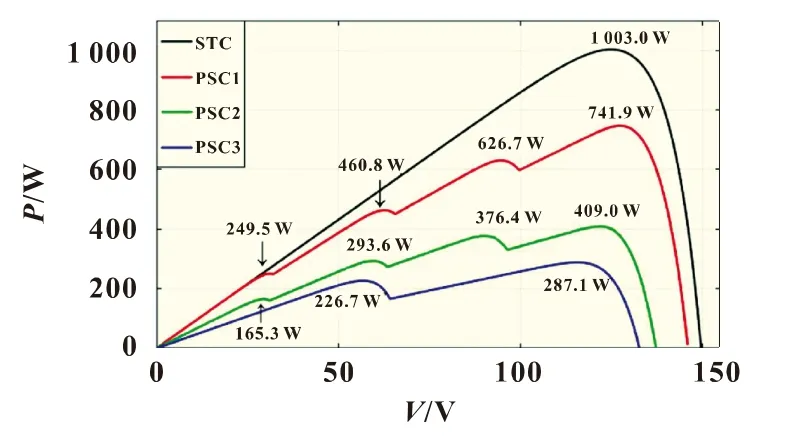
图4 不同情景下的光伏组件P-V曲线图

由图4可见在STC情况下只有一个峰值点(125.2 V，1 003 W)，面对这样的单峰值状况，寻优不会受到陷入局部最优的困扰；PSC1全局最大功率点为(124.4 V，741.9 W)，前三个都是局部最优值，其中与最大功率点较接近的一个为(92.6 V，626.7 W)；PSC2中全局最大功率点为(120.8 V，409 W)，前三个都是局部最优值，其中与最大功率点较接近的一个为(89.7 V，376.4 W)；PSC3中全局最大功率点为(116.2 V，287.1 W)。由图4可知，在整体辐照度较小时，局部最大功率点与全局最大功率点的差值并不大，传统的MPPT方法很难达到这样的精度要求，往往会陷入局部最优。

3.2 标准测试环境条件下仿真

首先进行标准测试环境STC下的仿真，仿真结果如图5所示。

由图5可见，在面对简单的单峰值P-V特性曲线时，包括传统的爬山法的三种方法皆可完成寻优任务。本文提出的控制策略较PSO和爬山法在搜索速度上有了较大提升，在0.05 s时三种方法都进入了稳定的状态，且CSA与爬山法的协同控制策略仿真得到的最大功率点稳定在1 003 W附近，只有幅度为1 W的小幅振荡，两者协同的控制效果在STC下效果极佳。爬山法稳定后在963.8～1 000 W有幅度将近40 W的振荡。PSO在三者中搜索速度最慢，在搜索到最大功率后仍有一定幅度的振荡，造成功率的损失。

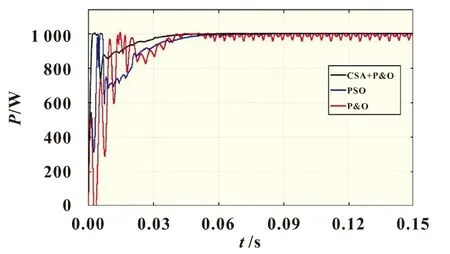
图5 STC的MPPT仿真

3.3 环境参数变化条件下仿真分析

在实际工作过程中，温度和辐照度实时变化，任一条件变化都会影响光伏组件的输出。将分为静止和动态变化两种情况进行测试。先将测试条件设置为PSC2进行仿真分析，结果如图6所示。

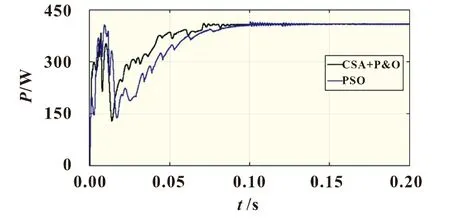
图6 对PSC2的MPPT仿真

由图6可知，在辐照度和温度不均的情况下，P-V特性曲线出现多峰值时，布谷鸟算法与爬山法的联合控制与PSO算法搜索到全局最大功率点。相较于PSO算法，本文所提算法的寻优速度加快了0.04 s，PSO算法稳定在402.3～414 W，震荡幅度为12 W，而本文所提控制策略稳定在408.5 W，其中震荡幅度只有不到1 W，精度也提升较大。实际工况光伏组件所处的环境变化多样且快速，所以也要对本文所提算法在这种情况下的性能进行验证。为了模拟外界环境快速变化时的情景，设定初始条件为STC，在0.2 s时变为PSC1，在0.4 s时变化为PSC2，在0.6 s时变化为PSC3。将本文所提MPPT策略与PSO进行比较，仿真结果如图7所示。

面对环境参数快速变化的情况下，在四种不同的环境中全局峰值点分别是1 003、741.9、409和287.1 W，在多次仿真过程中，PSO控制的MPPT有时会在环境参数变化处失效，陷入局部最优解，而CSA与P&O的联合控制每次都可以精准寻找到全局最大功率点。本文选取两种方法都寻优成功的一次来进行分析比较，在面对环境变化的情况下，布谷鸟算法和爬山法的联合控制基本可在0.04 s内重新搜索到系统的全局最优解，追踪速度较PSO算法控制有了约0.02 s的提升。且在完成寻优后更加稳定，与PSO完成后4 W的振荡相比，其振荡幅度只有1 W，基本可以忽略不计，大幅度改善了输出功率的波形品质，减小了功率曲线的震荡幅度，提升了光伏组件的输出效率，减小了因振荡产生的损耗。

4 结束语

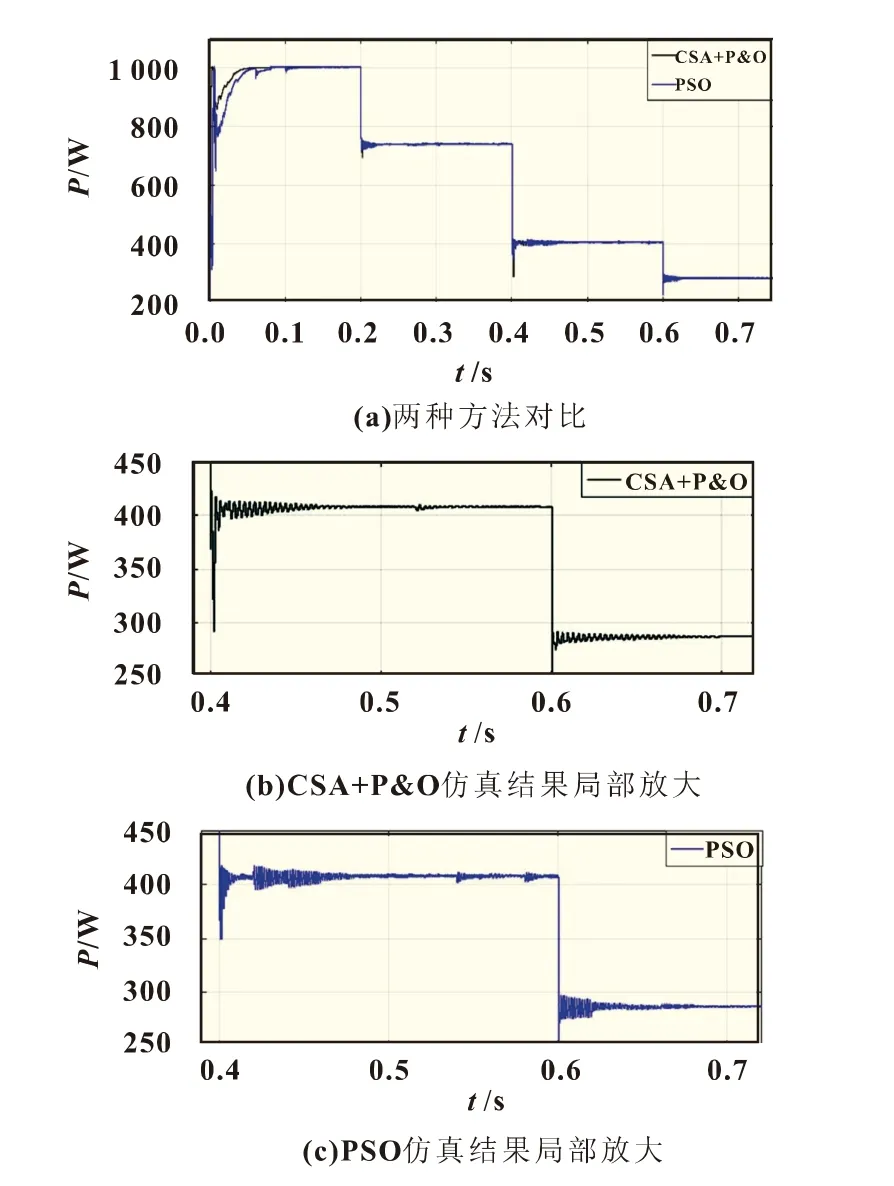
图7 对快速变化环境下的MPPT仿真

本文提出了一种布谷鸟搜索算法与爬山法协同控制的MPPT方法，减少了布谷鸟算法在搜索过程后期因Levy飞行的随机步长产生的大量计算，在兼顾全局搜索与局部搜索的策略下，可以精准快速地寻找到MPP。在MATLAB/Simulink中搭建系统，对本文所提方法在光伏系统中应用的效果进行验证，并且与爬山法和粒子群算法进行对比，证明了布谷鸟搜索算法与爬山法在静态和动态变化环境条件下都可以快速准确地搜索到全局最大功率点，同时减小了因振荡产生的功率损失。