基于全局比较的光伏电池MPPT实验研究
2021-02-01徐川翔吴丹丹
徐 金,葛 强,李 娟,徐川翔,吴丹丹
(扬州大学电气与能源动力工程学院,江苏 扬州 225127)
近年来,环境污染、温室效应以及能源危机等问题日趋严峻,光伏产业作为环境友好型能源的代表,在工业生产中的应用占比日益提升,各国对光伏产业的重视程度日益深化,研究人员通过改变材料、研究算法、寻找最佳光伏方位角等手段[1-2],使得光伏产业在高效性、稳定性、安全性等方面取得巨大进步[3],可靠的最大功率点追踪控制方法对提高光伏电站的发电效率具有现实意义。传统最大功率点追踪的控制方法研究一直在进步,从早期通过对光伏电池进行串并联组合来寻找最大功率点,发展到基于DC-DC电路的电压环、电导环、功率环[4-5]等光伏电池最大功率点控制策略,目前光伏行业中使用最为广泛的控制方法是扰动观察法(perturbation and observation method,P&O)[6-7]。
国内研究人员提出的变步长扰动观察法,虽加入更加优化的闭环控制提高了光伏电池的发电效率,但实际情况下光伏电池难免出现受建筑物、灰尘、鸟类粪便等阴影遮挡的现象[8],此时光伏电池的功率曲线以及电压曲线会发生变化,导致传统控制方法容易对最大功率点产生误判,不能满足快速追踪到最大功率的要求,并且在一定程度上造成能源浪费。智能算法在光伏电站中的应用也逐步增多,诸如神经网络控制算法、模糊控制算法等,但由于算法核心专家库函数针对不同环境时难以编写,难度提高的同时,也增加了光伏电站运营成本,经济性较差[9-10]。
本文提出一种基于全局比较的MPPT控制策略,该算法通过检测并比较光伏电池开断功率以加快追踪最大功率点的同时也提高了追踪最大功率点的准确性,且能满足不同辐照工况下的光伏实验和工程需求,具有极大的光伏产业实际应用价值。
1 光伏电池阴影遮挡情况下输出特性分析
光伏电池的I-U方程为:
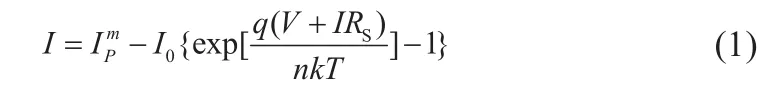
式中:I为输出电流;IP m为第m个组件单元的光生电流;I0为反向饱和电流;q为电子电量;V为输出电压;RS为串联电阻;n为二极管因子;k为玻尔兹曼常数;T为绝对温度[11]。
图1是光伏电池模型,由图可见若干小单元串联构成一个组件,每个组件外并联一个旁路二极管(各组件串联连接)[12],假设第二个光伏组件存在阴影遮挡,则其接受的光照强度小于其他组件,则光生电流应满足如果整个光伏电池对外输出的电流I满足,则光伏电池组件都处于正常发电状态,U-P曲线只有1个功率极点;如果电流I满足,大于IP2的电流会流经第2个组件产生正向电压,当达到二极管的导通电压时,旁路二极管导通,形成续流回路,对外不产生电压,直接导致最大功率点工作电压发生偏移,此时的U-P曲线有2个功率极点。以此类推,假设存在不同面积的阴影遮挡时,光伏电池的U-P曲线会存在多个功率极点。图2是多个功率极点的U-P曲线图。由图可见,当光伏电池存在不同程度遮挡并且配备不同个数并联二极管时,会出现功率多极点的情况,光伏电池最大功率对应的工作电压会发生移动。
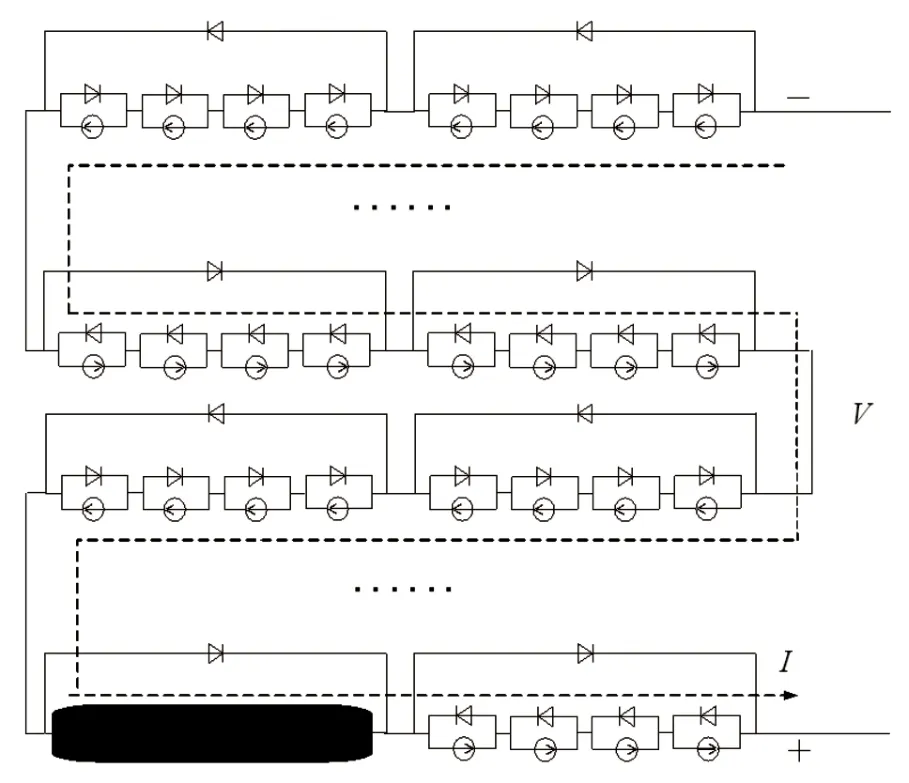
图1 光伏电池模型

图2 多个功率极点U-P曲线
2 基于全局比较的MPPT组合算法
2.1 扰动观察法原理及缺陷
光伏电池中最重要的两组参量分别是A组(开路电压、短路电流)、B组(光照强度、温度),而根据光伏电池的输出特性曲线可知,B组的变化是外界变化,极易影响A组参量,而A组中电流量只有越过最大功率点时才会发生剧烈变化,因此选择电压参量作为最佳控制量。扰动观察法原理是以电压步长作为扰动量,扰动量取值过大,系统响应快,但会出现较大功率振荡,扰动量取值过小,追踪功率较精确,但系统响应慢,同时该算法只能够寻找到离起始扰动电压最近的功率峰值,一旦光伏电池发生被遮挡而出现多个功率极点,该方法就存在误判断或重新判断导致响应速度慢的情况。
假设扰动观察法的起始扰动电压为光伏电池的开路电压,出现图2中(a)(b)(c)三种情况时,算法执行后会出现以下两种结果:(1)只有单功率极点时,算法会准确地找到最大功率;(2)存在2个或3个功率极点时,算法会在距离开路电压最近的伪最大功率点周围左右徘徊。
对于第二个结果,光伏电站的整体效率会有所下降,因此需要一种能够正确找到最大功率点的算法。
2.2 DC-DC拓扑结构
本次实验研究采用Boost升压电路,其拓扑结构如图3所示。升压电路由电流传感器CM、电压传感器VM、电容C、电感L和金属-氧化层半导体场效晶体管(metal-oxide-semiconductorfield-effect-transistor,MOSFET)等模块构成。
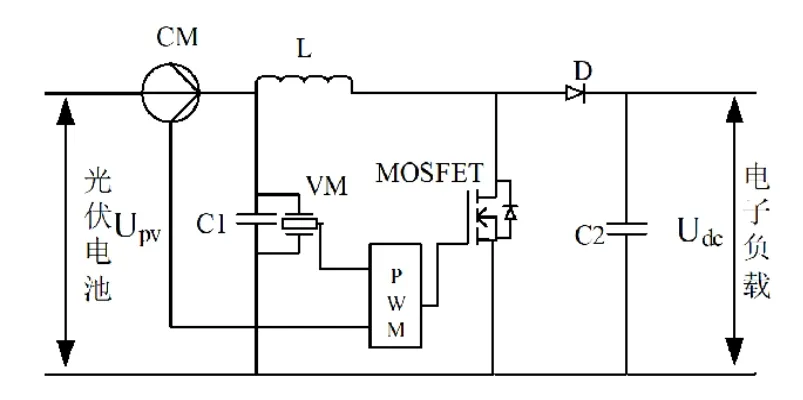
图3 升压电路拓扑
以MOSFET通断一周期为时间T,导通时间为ton,电路电流为I1,关断时间为toff,电流为I2,电感电压决定了电流的上升率:

由电流变化规律可联立:

最后可得光伏电池输出电压与负载电压的关系式为:
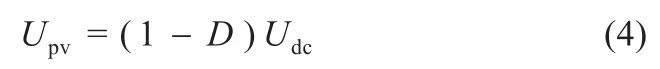
实际操作过程中电子负载将负载电压固定,只需通过改变MOSFET的占空比D,便可以顺利追踪至光伏电池最大功率。
2.3 全局比较法可行性分析
光伏电池前端电路中有开路电压UOC,短路电流ISC,瞬时电压U,瞬时电流I,以端口电路从短路到开路的过程为一个周期T,在此周期中四者满足对应关系式:0<U<UOC,ISC>I>0,且在较短的周期内,电压可近似为线性变化。图4为标准工况下电压电流功率曲线。由图4可见,在一个周期内,功率曲线出现上升段与下降段的交点,即为当前周期内的最大功率点,其所对应的电参数为周期内最大功率点工作电参数。
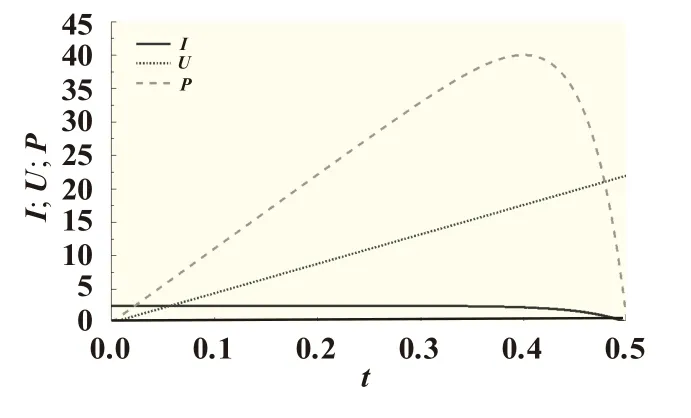
图4 标准工况下电压电流功率曲线
当光伏电池存在阴影遮挡时,被遮挡光伏组件与其并联的旁路二极管形成续流回路,光伏电池产生的光生电流急剧下降,对外表现的最大工作电压变小,直接导致最大工作电压偏移,但在遮挡后其电参数性质还是与图4所示类似,因此全局比较算法依旧是可行的。
2.4 MPPT组合算法设计
组合算法以扰动观察法为基础,全局比较法为辅的一种光伏控制策略,图5为组合算法流程图。
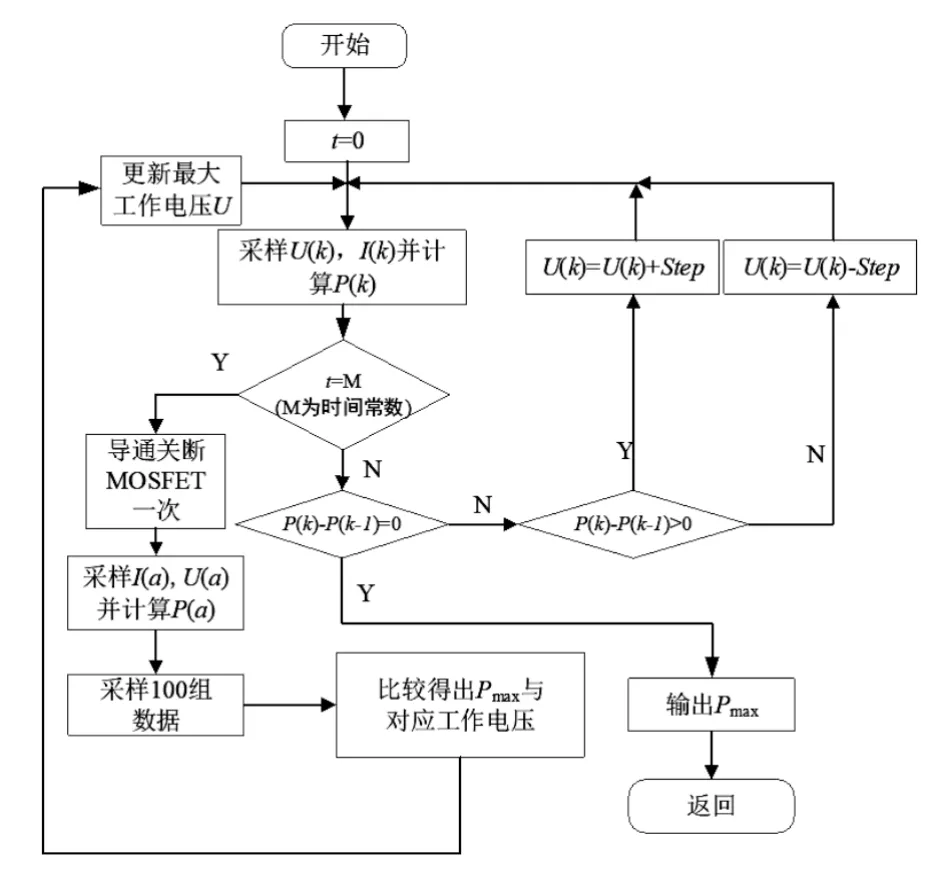
图5 组合算法流程图
由图5可见,整个算法将按照如下步骤运行一个周期:
(1)由于整个算法的基础是扰动观察法,因此先设置扰动观察法电压步长Step、扰动起始电压、系统采样频率f、扰动观察法运行时长t,通过控制器产生脉冲宽度调制信号(pulse width modulation,PWM)控制MOSFET。
(2)开始电压电流采样,计算功率,判断扰动观察法是否结束,未结束将当前时刻功率与前一时刻功率做差,如差为正,则增加一个电压步长,如差为负,则减少一个电压步长。
(3)当运行完扰动观察法后,使MOSFET通断一次,设定全局比较采样组数a,随即采样电压、电流并计算得出全局比较周期内最大功率。
(4)将全局比较的最大功率与扰动观察法最大功率相比较,如果两者相等则继续进行扰动观察法,如果两者功率不等将电压值更新为全局比较最大功率点电压后再进行扰动观察法。
3 实验分析
为了证明算法的实际可操作性,通过搭建光伏实验平台对基于全局比较的MPPT控制算法进行实验论证。在做对比实验时,遮挡面积会影响光伏电池的发电效率,为了更好地论证算法优势,本文采用两种不同面积的阴影,分别采用扰动观察法以及基于全局比较的组合算法进行分析比较。本次实验采用的光伏电池由6行12列的72个单晶硅单元组成,在两种不同的光照强度情况下进行实验,实验时在2 s左右时遮挡左上2行12个电池单元(1/6遮挡),在1 s左右时遮挡左上4行24个电池单元(1/3遮挡)。
组合算法设定参数:电压步长Step为1 V,起始扰动电压Us=35 V,采样频率f=5 000 Hz,时间常数M=10 s,全局比较采样组数a=100。实验光伏电池参数:在标准情况下(25℃,1 000 W/m2)额定功率Pe=100 W,最大功率点电压Um=24.5 V,最大功率点电流Im=4.14 A,开路电压UOC=44.0 V,短路电流ISC=5.49 A,旁路二极管3个。实验电路参数:电感L=10 mH,电容C=470µF,电子负载设置为50 V恒压负载。实验条件:光照强度S1=700 W/m2以及S2=460 W/m2,时间t1=11 s以及t2=7 s。
图6为不同遮挡及不同光照条件下扰动观察法与组合算法追踪性能对比。
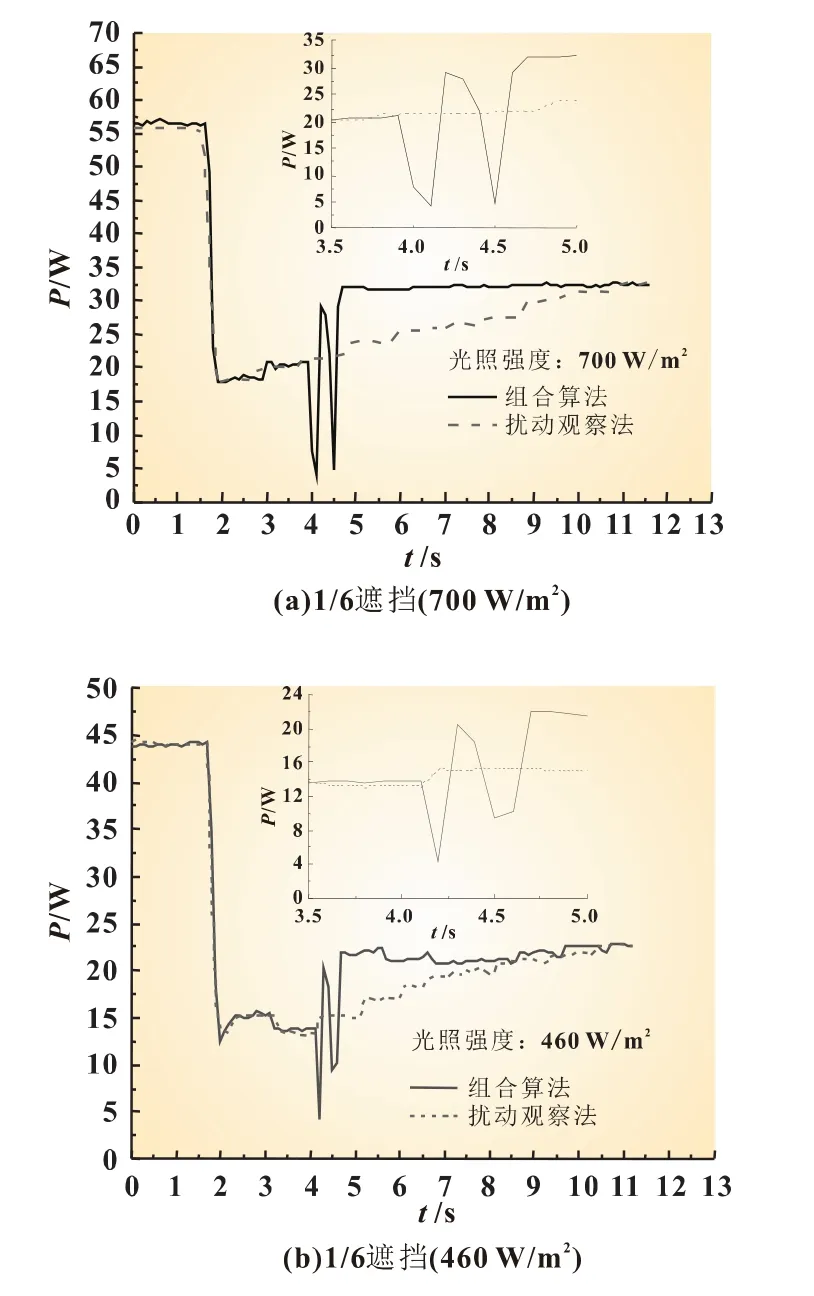

图6 扰动观察法与组合算法追踪性能对比
由图6可见:
(1)组合算法产生电能比扰动观察法分别提升约9.3%、10.9%、7.7%及11.7%,输出电能更高效;
(2)相同光照强度时,组合算法在小面积遮挡下重新追踪到最大功率用时分别为2.5和2.6 s,而在大面积遮挡情况下重新追踪用时分别为2.8和2.7 s,小面积遮挡下重新追踪最大功率更有优势,与光伏电池运行时大多出现小面积遮挡的情况相符,适用性强;
(3)相同遮挡情况下,组合算法在低光强时发电效率较高光强时有显著提升,弥补了传统扰动观察算法在低光照强度时不敏感的缺陷。
综上所述,基于全局比较的光伏MPPT组合算法可以更好地解决光伏电池在阴影遮挡下的快速最大功率追踪且环境适应性强,对光伏电池发电效率有显著提升。
