河道格宾石笼护坡破坏模式及稳定分析
2021-02-01黄绪红刘福臣
黄绪红,刘福臣
(1.平阴县锦水河流域水利站,山东 济南 250400;2.山东水利职业学院,山东 日照 276826)
格宾石笼具有抗冲能力强、整体性强、耐腐蚀、柔性好、能适应河床变形等优点,已广泛应用于河道护岸工程中。关于格宾石笼护坡的研究施工工艺、应用研究的文献很多[1-3];蒋洋[4]对石笼单体结构应力—应变特征进行试验研究,指出了石笼单体结构的强度源于铁丝笼和填石的综合作用,是两者的复合体;易明珠[5]对格宾挡墙应力变形特性试验研究及计算分析,以案例形式采用有限元的方法,分析了格宾挡墙的应力应变特性,为工程设计提供参考。关于格宾石笼护坡破坏模式及稳定分析没有文献报道,本文全面分析格宾石笼护坡的工作原理、受力特点、破坏机理,探索建立格宾石笼护坡破坏模式,提出各种破坏模式的适用条件及计算方法。
1 沿石笼与土体接触面滑动破坏模式
石笼质量较好,在外荷载作用下,不可能在石笼之间产生滑动。破坏时首先沿着石笼与土体之间的接触面滑动,然后沿着石笼底部滑动,最终在河床内土体形成滑动面冲出河床,形成复合折线滑动面ABCDE(见图1)。

图1 沿石笼与土体接触面滑动示意
折线滑动稳定安全系数主要有等安全系数法、抗力体极限平衡法。
1.1 等安全系数法
假设3个滑块的抗滑安全系数相等,即K1=K2=K3=K。
第1滑块ABCGJH:假设第1滑块对第2滑块产生的不平衡推力大小为P1,方向沿着第1滑块的滑动方向,根据作用力与反作用力原理,第2滑块对第1滑块产生的抵抗力大小为P1,方向与第1滑块滑动方向相反。
下滑力为W1sinα1,抗滑力为f1W1cosα1+P1,抗滑安全系数为:
(1)
式中W1为石笼护坡的重力,kN/m;f1为第1滑块与土体之间的摩擦系数;α1为石笼护坡的倾角,°;P1为第1滑块产生的不平衡推力,kN/m。
由式(1)解得不平衡推力为:
P1=KW1sinα1-f1W1cosα1
(2)
由于每层石笼外挑深入土中,只有石笼的一个角点属于石笼与土体之间滑动,大部分在土中通过,所以第一滑块与土体之间的摩擦系数f1=tanφ1。
第2滑块CDFG:滑动面为水平面,该滑块作用力有P1(沿第1滑块滑动方向)、P2(与水平滑动方向相反)、重力W2(方向向下),则下滑力为P1cosα1,抗滑力为(W2+P1sinα1)f2+P2,抗滑安全系数为:
(3)
式中W2为石笼护底的重力,kN/m;f2为石笼护底与土体之间的摩擦系数;P2为第2滑块产生的不平衡推力,kN/m。
石笼与地基之间的摩擦系数受到各种因素的影响,其大小与石笼底部理砌的石块大小、摆放形式、地基软硬程度、石笼的钢丝有关。石笼底石块粒径大,且大小较均匀、理砌规整,地基土较硬,石笼与地基之间可形成一直线滑动面,石笼与地基之间的摩擦系数可近似取干砌石与土的摩擦系数;石笼底石块大小不一,地基土较软,只能在土中形成直线滑动面,不可能沿着石笼底部滑动,摩擦系数可近似取土的内摩擦系数,即f2=tanφ2。设计时可根据具体情况综合分析,选取合理的摩擦系数。
由式(3)解得不平衡推力:
P2=KP1cosα1-(W2+P1sinα1)f2
(4)
第3滑块DEF:该滑块滑动力P2cosα3,抗滑力为:W3sinα3+W3cosα3tanφ2+P2sinα3tanφ+c2l,抗滑安全系数为:
(5)
式中W3为第3滑块的重力,kN/m;α3为第3滑块滑动面的倾角,°;φ2为河床土体内摩擦角,°;c2为河床土体凝聚力,kPa;l为第3滑块的滑动面长度,m。
由式(2)(4)代入式(5)整理得到安全系数为一元三次方程,可以求出安全系数K的理论解。
必须注意,由于第3滑块的滑动面的倾角α3未知,可假定一系列α3值,求出最小安全系数即为整个折线滑动的安全系数。
1.2 抗力体极限平衡法
滑动体是产生滑动的主要发动者,所以称为主动体;滑动体主要起到抵抗滑动作用,又称为抗力体。抗力体极限平衡法即假设:从第1块滑动体开始,假设其处于极限平衡状态,计算出剩余推力,依次向下传递,求出最后1块滑动体(抗力体)的安全系数,作为为整个折线滑动的安全系数。
即令式(1)安全系数K=1,求得:
P1=W1sinα1-f1W1cosα1
(6)
同样令(3)安全系数K=1,求得:
P2=P1cosα1-(W2+P1sinα1)f1
(7)
将P1、P2代入式(5)得到抗力体的安全系数:
(8)
研究分析表明[6]:等安全系数法计算的安全系数较抗力体极限平衡法计算值偏小,建议采用等安全系数法计算复合折线滑动安全系数。
2 沿土体内滑动面、石笼与土体接触面、河床土体滑动面滑动破坏模式
石笼质量较好,整个石笼作为整体承受土压力。如果石笼后的填土质量较差,破坏时首先在填土内产生滑动面,产生主动土压力。在土压力作用下,不可能在石笼之间产生滑动,破坏时只能沿着石笼底部滑动,最终沿河床内土体形成滑动面冲出河床,形成折线滑动ABCDE(见图2)。其中θ为破裂面的倾角。
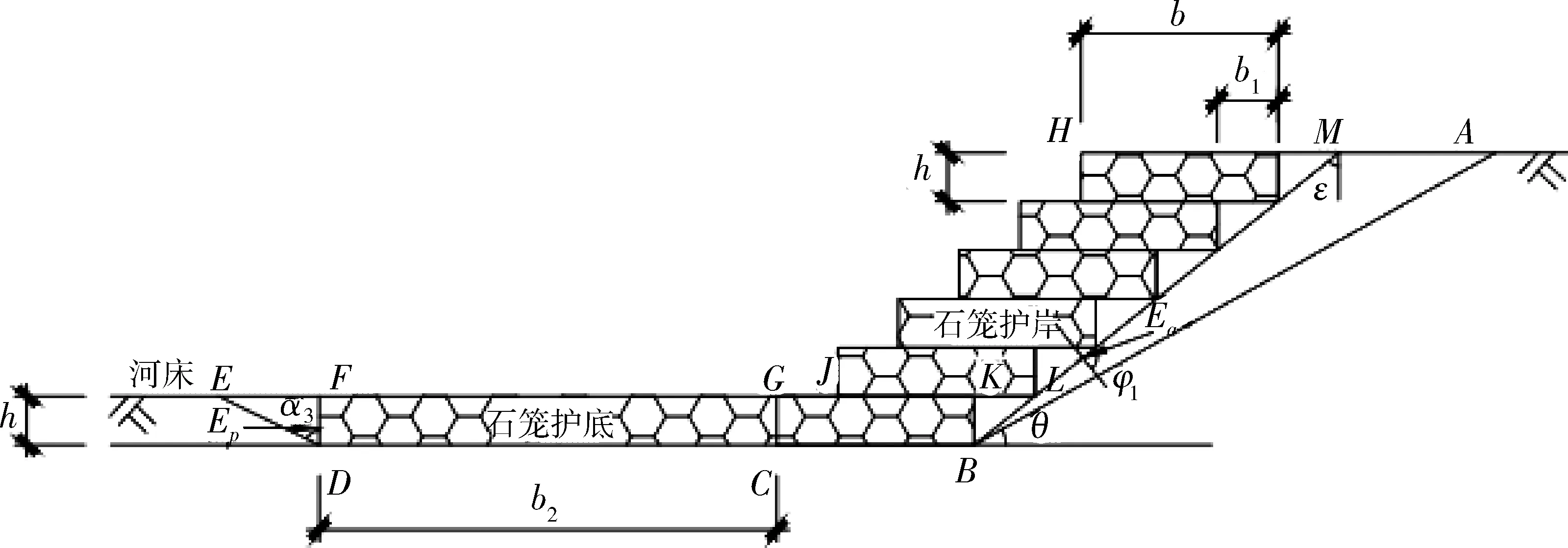
图2 沿土体内滑动面、石笼与土体接触面、河床土体滑动面滑动
2.1 主动土压力
对于无粘性土,库仑主动土压力按下式计算:
(9)
(10)
式中Ka为库仑主动土压力系数;H为挡土墙高度,m;γ1为墙后填土的重度,kN/m3;φ1为墙后填土面的内摩擦角,°;ε为墙背的倾角,°(墙背俯斜时取正号,仰斜时取负号);β为墙后填土面的倾角,°;δ为土对挡土墙墙背的摩擦角,°。

(11)
主动土压力沿水平方向、垂直方向分力为:
Eax=Eacos(φ1-ε)
(12)
Eay=Easin(φ1-ε)
(13)
2.2 被动土压力
对于无粘性土,护底采用单层格宾石笼,河床内的土体DE面上产生的被动土压力为:
(14)
(15)
式中Kp为朗肯被动土压力系数;φ2为河床内的土体的内摩擦角,°;γ2为河床内的土体的重度,kN/m3。
2.3 石笼与地基之间产生的摩阻力
在垂直水流方向上,假设石笼护坡剖面(不包括基础部分)为单排石笼,石笼层数由下而上的的编号为1,2,3…n,单个石笼的重力为:
W0=γ石笼bh
(16)
式中γ石笼为石笼重度,kN/m3。
石笼重度与填充料的粒径大小、级配、材质、施工质量有关,可在工地上进行现场率定。一般情况γ石笼=20~22 kN/m3。
与单个石笼一起滑动的倒三角形土体底宽为b1,高为h,重力为:
(17)
(18)
式中n为不包括石笼在内的护岸石笼层数。
抗滑安全系数:
(19)
3 沿两层石笼之间滑动面滑动破坏模式
护坡石笼高度大,石笼内填石粒径偏小,石笼重量较轻,或者石笼之间的绑扎数量偏少,破坏时首先在填土内产生滑动面,产生主动土压力。在土压力作用下,沿着石笼与石笼之间的接触面滑动,由于土压力随深度增加,所以,最有可能在底部两层石笼之间产生滑动破坏(图1中的JKL)。
不计石笼之间的连接绑扎线的抗剪强度,沿两层石笼之间抗滑安全系数为:
(20)
将WEaxEay代入式(20)得到:
(21)
式中f综合为上下两层石笼之间的综合摩擦系数。
3.1 滑动面长度
图1中的JKL为底部石笼之间滑动面,其总长度为b,由两部分组成:一是石笼之间的滑动面,长度JK=b-b1;二是石笼与填土之间的滑动面,长度LK=b1,每个滑动长度对应滑动摩擦系数并不相同。
3.2 两层石笼与石笼之间的综合摩擦系数f综合
设f2为石笼与土体之间的摩擦系数;f3为石笼与石笼之间的摩擦系数,综合摩擦系数f综合可采用加权平均求得:
(22)
f3的大小与石笼界面的平整度、石笼的钢丝网孔尺寸等因素有关,界面越平整度,石笼之间的摩擦系数f3越小;界面越不平整度,石笼之间的摩擦系数f3越大;网孔尺寸越小,滑动面上下两层的钢丝接触面积越大,石笼之间的摩擦系数f3越小。
4 沿石笼外缘倾覆破坏模式
如果石笼护坡高度较大、坡度较陡,墙后填土质量较差时,在主动土压力作用下,石笼护坡可能绕墙趾点(图1中的J点)向外倾覆发生破坏。
4.1 重力产生的力矩M重
4.1.1石笼重力产生力矩M石笼重
(23)
(24)
0+b1+2b2+…+(n-1)b1,为一等差数列,差数列之和为:
(25)
a1=0,级差d=b1,则式(24)为:
(26)
4.1.2石笼墙背后的倒三角形土体重力产生力矩M土体重
(27)
(28)
0+b1+2b2+…+(n-1)b1为一等差数列,求其和代入式得到:
(29)
M重=M石笼重+M土体重
(30)
4.2 主动土压力分力产生的力矩

主动土压力垂直分力产生的力矩Eayxf,力臂xf由下式计算:
(31)
4.3 抗倾覆安全系数
抗倾覆安全系数为:
(32)
5 深层整体滑动破坏模式
当地基土性质较差,抗剪强度较低时,石笼连同河堤部分土体沿着地基内部产生深层整体滑动破坏。其滑动面一般为圆弧,称为圆弧滑动,可采用条分法计算。深层整体滑动条分法,就是将滑动土体分成若干垂直土条,分析每一条上的作用力,然后利用每一土条上的力和力矩的静力平衡条件,求各土条对滑弧圆心的抗滑力矩和滑动力矩,分别求其总和,然后再求出该土坡的稳定安全系数。常见的瑞典圆弧法、简化毕肖普法。
5.1 瑞典圆弧法
瑞典圆弧法的安全系数表达式为:
(33)
式中h1i为第i土条顶部石笼厚度;h2i为第i土条土体的高度;γ为土的重度;bi为第i土条宽度;li为第i土条滑动面的弧长;θi为第i土条滑动面倾角。
计算时可假设一系列圆心、滑弧半径,分别求得一系列安全系数,最小值为所求。
5.2 简化毕肖普法
简化毕肖甫法土坡稳定分析的安全系数表达式为:
(34)
(35)
式中Wi为第i土条包括上部格宾石笼、土体重力;ui为第i土条孔隙水压力;c′、φ′为土的有效凝聚力和内摩擦角。
式中mθi包含了安全系数Ks,故由式(34)尚不能直接计算Ks,而需要采用试算的方法,先假定Ks=1.0,由式(35)计算θi所对应的mθi,再代入(34)求得Ks1。若Ks1不等于1.0,则用计算的Ks1重新计算mθi值,再计算出Ks2,如此反复迭代,直至前后两次计算的安全系数十分接近,达到规定要求的精度标准为止。
6 结语
1)沿石笼与土体接触面滑动破坏模式,等安全系数法计算假设合理,计算的安全系数偏小,偏安全;抗力体极限平衡法假设不合理,计算的安全系数偏大,偏不安全,建议采用等安全系数法计算复合折线滑动安全系数。
2)沿土体内滑动面、石笼与土体接触面、河床土体滑动面滑动破坏模式,采用式(19)计算抗滑安全系数。
3)沿两层石笼之间滑动面滑动破坏模式,采用式(21)计算抗滑安全系数。两层石笼与石笼之间的综合摩擦系数f综合可采用加权平均法计算;石笼之间的摩擦系数f3可通过现场试验测定。
4)沿石笼外缘倾覆破坏模式,采用式(32)计算抗滑安全系数。
5)深层整体滑动破坏模式,可采用瑞典条分法和简化毕肖普法计算整体滑动安全系数,简化毕肖普法计算及条块间作用力,能反映土体滑动土条之间的客观状况,但计算比瑞典圆弧法复杂。
