用简化的水平条分法分析加筋土挡墙的稳定性

阮晓波，孙树林

（1.河海大学土木与交通学院，江苏 南京 210098；2.河海大学地球科学与工程学院，江苏 南京 210098）

1 研究背景

水平条分法是一种适合用于分析加筋土挡墙与边坡稳定性的极限平衡分析方法[1]，是由Lo&Xu[2]在1992年提出来的。当用水平条分法分析加筋土挡墙稳定性时，一般会在两个问题的确定上存在差异：一是破裂面的形状；二是条间力的情况。对于第一个问题，通过前人的研究发现：不论加筋土挡墙后填土破裂面是平面状的还是对数螺线状的，都可以用水平条分法分析加筋土挡墙的稳定性。对于第二个问题，由于条间力包括水平条间力和竖直条间力，所以条间力的确定存在两种情况。情况一，按水平条间力来分可以再分成两种情况：一是不考虑水平条间力[3-9]，在这里称这种方法为简化水平条分法；二是考虑水平条间力[1-2，10]，一般是基于 Morgenster&Price 的方法[11]来确定的。情况二，按竖直条间力来分也可以再分成两种情况：一是竖直条间力等于其上部的超载[1-7]，二是用Segrestin的方法[12]来确定竖直条间力的大小[8-10]。通常，水平条分法会结合拟静力分析方法[1-6，10]或者拟动力分析方法[7-9]来建立平衡方程，推导出待研究参数的计算公式或者方程式，进而对加筋土挡墙稳定性的影响因素进行研究分析。

本文是基于文献 [3]的方法和文献 [5]的破裂模型，采用拟静力-简化水平条分法推导出地震条件下加筋土挡墙后填土中有地下水时所需筋材拉力总和的计算公式和临界破裂角的方程式，计算公式考虑了地震力、静水压力、动水压力、加筋土挡墙后填土的黏聚力和内摩擦角等因素，并且研究了它们对所需筋材拉力总和或者所需筋材拉力总和系数的影响。

2 公式推导

2.1 基本假设

用拟静力-简化水平条分法进行计算公式推导时，做了如下假设：

1）加筋土挡墙垂直水平面，挡墙后填土顶部水平，并且不考虑其上部所受的超载；

2）加筋土挡墙的加筋材料为可延展性材料，破裂面为平面状，并且通过挡墙的墙趾，如图1所示；

图1 加筋土挡墙水平土条的划分

3）加筋土挡墙后填土的整个滑动体被分为n个水平土条，每个土条包含一层筋材，每个土条的竖向条间力等于其上部的超载，每个土条上的安全系数FS均相等；

4）不考虑加筋土挡墙后填土的遇水膨胀、湿陷以及地下水位以上和以下内摩擦角的不同。

2.2 建立平衡方程

对于地下水位以上和以下土条的受力分析如图2所示，Vi、Vi+1、Vj、Vj+1为土条所受的竖向条间力；Hi、Hi+1、Hj、Hj+1为土条所受的水平条间力；Qhi、Qhj为土条所受的水平地震力，并且Qhi=khWi，Qhj=khWj；Qvi、Qvj为土条所受的竖向地震力，并且Qvi=kvWi，Qvj=kvWj；kh、kv分别为水平和竖向地震力加速度系数；Wi、Wj为土条所受的重力；Ni、Nj为土条破裂面上的法向反力；Si、Sj为土条破裂面上的切向反力；Ti、Tj为土条所受的筋材拉力；Pstdj、Pdynj为土条所受的静水压力和动水压力。如图1所示，加筋土挡墙竖直高度为H，地下水深度为Hw，破裂面与水平面所成角度为α；挡墙后填土被分为n个土条，地下水位以下有l个土条，每个土条高为h，破裂面长度为li；加筋土挡墙后填土的黏聚力和内摩擦角分别为c和φ。

对于地下水位以上的土条，其竖直方向上力的平衡方程为，∑Fy=0，即：

图2 土条受力图

对于地下水位以下的土条，其竖直方向上力的平衡方程为，∑Fy=0，即：

其中，Wj=γsath（2H-2jh+h）cot α，γsat为加筋土挡墙后填土的饱和重度。

破裂面上的切向反力和法向反力的关系，即：

其中，li=lj=。

对于加筋土挡墙后填土的整个滑动体，水平方向上力的平衡方程，∑Fx=0，即：

对于作用在破裂面上的总静水压力Pstd，可以用Ebeling&Morrison的方法[13]来确定：

其中，γwe= γw+为加筋土挡墙后填土的等效重度；γw为水的重度；ru为孔隙水压力比，并且

对于作用在破裂面上的总动水压力Pdyn，可以用Westergaard的方法[14]来确定：

2.3 计算所需筋材拉力总和

由式（1）～式（6），可以推导出所需筋材拉力总和的计算公式，即：

根据文献 [15]，可以对所需筋材拉力总和进行归一化处理，化为K，即K=

2.4 计算临界破坏角

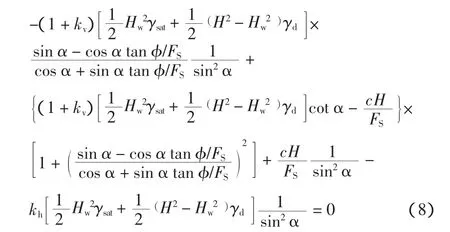
3 参数分析

3.1 临界破坏角

临界破坏角可以由方程式（8）求出来。本文是用MATLAB的fzero函数进行求解的。所求得的结果如表1和表2所示。其中，表1中已知参数有：kh=0.2，kv=0.1，FS=1.0，H=5.0 m，Hw=0，γd=18 kN/m3。c在 0～15 kPa之间变化，φ在20°～35°之间变化。表2中已知参数有：kv=0，c=0，FS=1.0，H=5.0 m，Hw=0，γd=18 kN/m3。kh在 0～0.2 之间变化，φ 在 20°～35°之间变化。

表1 加筋土挡墙后填土的黏聚力和内摩擦角对临界破裂角的影响（°）

表2 加筋土挡墙后填土的内摩擦角和水平地震力加速度系数对临界破裂角的影响（°）

从表1中可以看出，随着c的增加，临界破坏角在增大；从表2中可以看出，随着kh的增大，临界破坏角在减小；从两表中同时可以看出，随着φ的增大，临界破坏角也在增大。当c=0，kh=0和kv=0同时等于零时，临界破裂角等于Rankine法确定的破裂面角，但以上元素一有变化时，破裂面角就会随之变动。因此，当有地震力作用或者挡墙后填土为黏性土时，文献 [6]依据Rankine法确定的破裂面角就是不合理的。

3.2 竖直地震力加速度系数

表3讨论了φ和kv对临界破裂角和T的影响。其中，已知的参数有：kh=0.2，c=0，FS=1.0，H=5.0 m，Hw=0，γd=18 kN/m3。

表3 加筋土挡墙后填土的内摩擦角和竖向地震力加速度系数对临界破裂角和所需筋材拉力总和的影响

从表3中可以看出，随着φ的增大，临界破裂角在增大，T在减小，这说明大的φ有利于加筋土挡墙的稳定，并且可以节省筋材；随着方向向下的kv增大，临界破裂角在增大，T也在增大，这说明若要抵抗方向向下的地震力需要筋材的抗拉强度够大，但对筋材的长度要求不大；随着方向向上的kv增大，临界破裂角在减小，T也在减小，这说明若要抵抗方向向上的地震力需要筋材的长度够长，但对筋材的抗拉强度要求不大。这与Ling&Leshchinsky的研究结果[16]一致。由于本文主要研究T和K，所以选取方向向下的kv为主要研究对象。

3.3 地下水

在我国东部沿海地下水比较旺盛的地区建造加筋土挡土墙时，就不得不考虑地下水对挡土墙稳定性的影响。

如图3和图4所示，描述了Hw、φ和ru对K的影响。

图3 地下水深度和加筋土挡墙后填土的内摩擦角对所需筋材拉力总和系数的影响

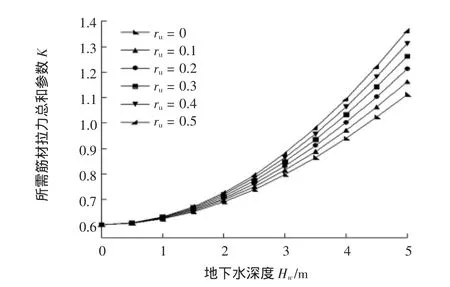
图4 地下水深度和孔隙水压力比对所需筋材拉力总和系数的影响

其中已知的参数有：kh=0.2，kv=0.1，c=0，FS=1.0，H=5.0 m，γd=18 kN/m3，γsat=20 kN/m3，γw=10 kN/m3。

在图 3中， ru=0.2，φ 在 20°～35°之间变化，Hw在 0～5 m之间变化；在图4中，φ=25°，ru在0～0.5之间变化，Hw在0～5 m之间变化。从图3可以看出，随着Hw的增大，K在增大，随着φ的增大，K在减小；从图4中可以看出，随着Hw或者ru的增大，K都是在增大的。这说明：随着地下水水位的升高或者孔隙水压力比的增大，需要更大的筋材拉力来维持加筋土挡墙的稳定，或者说，在加筋土挡墙后填土中所用筋材条件一样的情况下，加筋土挡墙更容易失稳；在加筋土挡墙后填土中所用筋材条件一样的情况下，随着后填土黏聚力的增加，会更有利于加筋土挡墙的稳定。

4 结语

本文采用拟静力-简化水平条分法，在筋材是可延展性的条件下，推导出所需筋材拉力总和的计算公式，计算公式考虑了水平和竖向地震力、加筋土挡墙后填土的黏聚力和内摩擦角、地下水等影响因素，并且求出了临界破裂角的方程式。通过参数研究，可以看出，随着加筋土挡墙后填土的黏聚力和内摩擦角的增大将有利于加筋土挡墙的稳定；随着水平地震力加速度系数的增大将需要更大的筋材拉力来维持加筋土挡墙的稳定；随着方向向下的竖向地震力加速度系数的增大，临界破裂角和所需筋材拉力总和都是在增大的，相反，随着方向向上的竖向地震力加速度系数的增大，临界破裂角和所需筋材拉力总和都是在减小的，这与Ling&Leshchinsky的研究结果一致；随着地下水水位的升高或者孔隙水压力比的增大，所需筋材拉力总和系数增大，这说明需要更大的筋材拉力来维持加筋土挡墙的稳定。

本文在考虑地下水的影响时，忽略了加筋土挡墙后填土的黏聚力，把后填土看作是渗透性极好的土体，即孔隙水都是自由水，不存在受限水，对加筋土挡墙受其影响有待进一步的研究；同时，还忽略了地下水位以上和以下加筋土挡墙后填土的内摩擦角存在的不同，这一点也有待进一步的完善。

[1]NOURI A，FAKHER A，JONES C J F P.Evaluating the Effects of the Magnitude and Amplification of Pseudo-Static Acceleration on Reinforced Soil Slopes and Walls Using the Limit Equilibrium Horizontal Slices Method[J].Geotextiles and Geomembranes，2008，26（3）：263-278.

[2]LO S C R，XU D W.A Strain Based Design Method for the Collapse Limit State of Reinforced Soil Walls and Slopes[J].Canadian Geotechnical Journal，1992，29（8）：832-842.

[3]SHAHGHOLI M，FAKHER A，JONES C J F P.Horizontal Slice Method of Analysis[J].Geotechnique，2001，51（10）：881-885.

[4]NOURI H，FAKHER A，JONES C J F P.Development of Horizontal Slice Method for Seismic Stability Analysis of Reinforced Slopes and Walls[J].Geotextiles and Geomembranes，2006，24（3）：175-187.

[5]JIANG Jian-qing，YANG Guo-lin.A New Slice Method for Seismic Stability Analysis of Reinforced Retaining Walls[C]//Second International Conference on Intelligent Computation Technology and Automation，2009：164-167.

[6]蒋建清，杨果林.加筋土挡墙地震稳定性分析的水平条分方法[J].中国铁道科学，2009，30（1）：36-40.

[7]NIMBALKAR S S，CHOUDHURY D，MANDAL J N.Seismic Stability of Reinforced-Soil Wall by Pseudo-Dynamic Method[J].Geosynthetics International，2006，13（3）：111-119.

[8]SHEKARIAN S，GHANBARI A，FARHADI A.New Seismic Parameters in the Analysis of Retaining Walls with Reinforced Backfill[J].Geotextiles and Geomembranes，2008，26（4）：350-356.

[9]SHEKARIAN S，GHANBARI A.A Pseudo-Dynamic Method to Analyze Retaining Wall with Reinforced and Unreinforced Backfill[J].Journal of Seismology and Earthquake Engineering，2008，10（1）：41-47.

[10]AHMADABADI M，GHANBARI A.New Procedure for Active Earth Pressure Calculation in Retaining Walls With Reinforced Cohesive-frictional Backfill[J].Geotextiles and Geomembranes，2009，27（6）：456-463.

[11]MORGENSTERN N R，PRICE V E.The Analysis of the Stability of General Slip Surfaces[J].Geotechnique，1965，15（1）：79-93.

[12]SEGRESTIN P.Design of Sloped Reinforced Fill Structure[C]//Proceedings of Conference on Retaining Structures，1992：574-584.

[13]EBELING R M，MORRISON JR E E.The Seismic Design of Waterfront Retaining Structures[R]//US Army Technical Report ITL-92-11.Washington，DC，1992.

[14]WESTERGAARD H M.Water Pressures on Dams during Earth－Quakes[J].Transactions，1933，98（2）：418-433.

[15]LING H I，LESHCHINSKY D，PERRY E B.Seismic Design and Performance of Geosynthetic-reinforced Soil Structures[J].Geotechhnique，1997，47（5）：933-952.

[16]LING H I，LESHCHINSKY D.Effects of Vertical Acceleration on Seismic Design of Geosynthetic-reinforced Soil Structures[J].Geotechnique，1998，48（3）：343-373.