地波雷达目标检测跟踪联合处理粒子滤波方法

付尚生纪永刚黎 明王祎鸣

(1.自然资源部 第一海洋研究所,山东 青岛266061;2.中国海洋大学 工程学院,山东 青岛266100)

高频地波雷达(High Frequency Surface Wave Radar,HFSWR)是大范围海上船只目标监视监测的主要手段,它利用高频电磁波(3～30 MHz)沿海面爬行来实现超视距的目标(船只、低空飞机等)探测,可以实时提供运动目标的位置和航速航向等信息,探测距离最远可达300 km,因此它又被称地波超视距雷达[1-3]。传统的高频地波雷达目标探测方法采用的是先检测后跟踪(Detect-Before-Track,DBT)的思想,该方法对于回波能量较弱、信噪比较低的目标单时刻的检测效果不佳,从而使得连续时刻的目标跟踪性能下降。检测与跟踪联合处理方法可以解决弱目标检测困难的问题,其思路是:对单帧雷达回波数据不进行目标有无判断,而是利用目标在时空上的关联特性和杂波噪声的随机性,进行多帧数据累积,从而实现同一目标的回波能量累积,由此提高目标信噪比,完成目标的检测判决和航迹跟踪。检测与跟踪联合处理方法由于不设置检测门限,能充分利用目标回波谱的原始信息,即可减少先检测后跟踪过程中的点迹与航迹关联问题,亦可降低算法复杂度[4-6]。

目前,国内外已发展了多种检测前跟踪(Track-Before-Detect,TBD)方法,均可被用于实现地波雷达目标检测与跟踪联合处理。主要方法有:动态规划(Dynamic Programming,DP)法[7]、粒子滤波(Particle Filter,PF)法[10]和三维匹配滤波(3-D Matched Filters)法[9]等。其中,动态规划法将目标的轨迹搜索问题转换为最优寻迹问题,对目标跟踪采取批处理方法,主要侧重于目标检测的实现[7]。三维匹配滤波法可将运动目标的检测转换为三维变换域中寻找匹配滤波器的问题,但该方法在某些情况下会导致不可实现的穷尽式搜索,限制了其性能[8-9]。粒子滤波法将目标航迹跟踪问题转换为目标的概率密度函数估计问题,相对于动态规划、三维匹配滤波等方法,它具有估计的目标状态在理论上最优的特点,适合于类似地波雷达这种非线性、非高斯的系统,且因其递归结构特点算法容易实现[10-11]。目前,粒子滤波法已被应用于地波雷达目标跟踪,主要被用于传统的先检测后跟踪方法中的滤波步骤,还未被用于地波雷达目标检测与跟踪联合处理。粒子滤波法已被应用于天波雷达目标检测与跟踪联合处理,但鉴于天波雷达探测的是飞机等高速移动的目标,与地波雷达的船只目标特性存在较大区别,并且大多是基于仿真的研究,缺乏实测数据验证。因此,本文将粒子滤波方法应用于地波雷达船只目标的检测与跟踪联合处理,发展适用于海上船只目标检测与跟踪联合处理的自适应粒子滤波方法,以期解决复杂环境下的地波雷达目标检测和跟踪效果较差的问题,提高地波雷达目标的整体跟踪性能。

1 方法原理

1.1 粒子滤波法原理

在粒子滤波法中,通过使用序贯重要性采样方法对目标状态进行采样,得到一组带有权值的随机样本即“粒子”当采样的样本集足够大的时候,经过重要性采样获得的这组随机粒子就可以用来描述目标的后验概率密度函数p(x1:k|Z1:k)(x1:k={x j|j=1,2,…,k}表示目标的状态序列,Z1:k={z1,z2,…,z k}表示目标的量测值序列,l为似然比,k为自然数)。一般在经过多次迭代后,粒子会出现退化现象,因此,在重要性采样结束后,还需要对粒子进行重采样。最终目标状态的后验概率密度可表示为

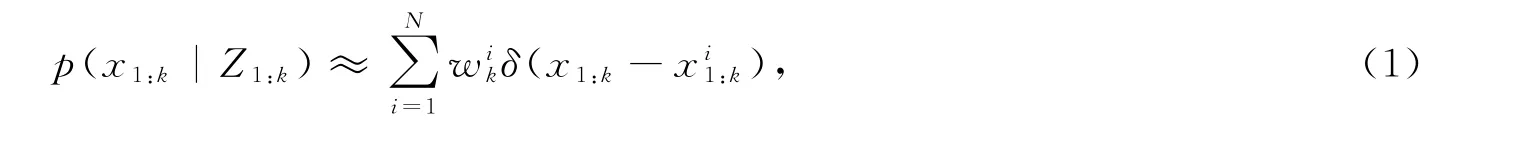
式中,i为自然数。

粒子滤波的粒子权重既可以构造检测似然比以实现目标检测,又可以通过粒子权重与粒子状态的加权估计目标的状态,从而实现目标的检测与跟踪联合处理。粒子权重与检测似然比之间的关系为

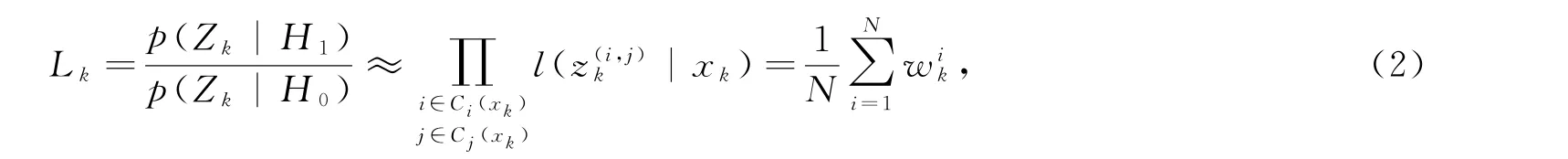
式中,L k为目标k时刻的似然比;H1为目标存在;H0为目标不存在;p(z k|H1)为目标存在时的概率密度;p(z k|H0)为目标不存在时的概率密度;C i和C j为受目标影响的单元;则目标k时刻的递归似然比计算公式为

将计算得到的目标似然比与设定的阈值进行比较,判断目标是否存在。若目标存在,则在完成粒子重采样后按照公式进行目标的状态估计。

1.2 基于粒子滤波的目标检测与跟踪联合处理方法

将高频地波雷达回波谱按照时间顺序排列构成三维R-D-T(Range-Doppler-Time)数据,如图1所示,其单帧RD谱的2个面目标如图2所示。由于受到目标本身特性(如目标自身的大小尺寸、相对于雷达的位置和运动速度等)和雷达系统参数(如频率、带宽和积累时间等)的影响,出现目标能量展宽现象,导致目标呈现为面目标。对于地波雷达目标探测,通常采用较长时间积累(100～300 s),以得到较高的频率分辨率并突显目标信号。在长时间积累过程中,运动目标的速度和所在距离会发生一定的变化,导致目标信号在多普勒维和速度维均发生一定的展宽(图2)。实际上,在雷达距离维,由于在雷达距离解调过程中存在加窗滤波处理,对于尺寸在几十米到几百米的目标,或者在积累时间内径向距离变化只有几十米到几百米,甚至精致不动的目标,也会在距离维上表现为一定的展宽。这种展宽现象对粒子滤波算法中的粒子初始化步骤会产生影响,因此,在对目标进行粒子采样的时候需要结合面目标特性设定粒子的采样范围,本文在距离[Rmin,Rmax]、多普勒[Dmin,Dmax]范围内均匀采样N个粒子,如图3所示,其中,灰色区域表示目标回波信号的展宽区域,黑色方格表示目标雷波回波中的峰值位置。

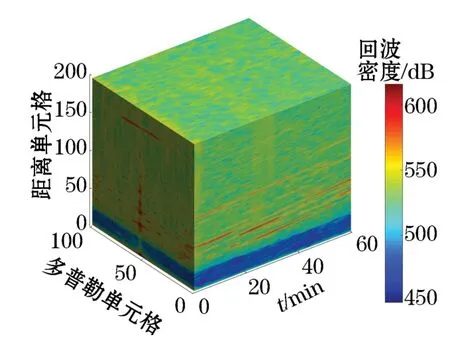
图1 R-D-T三维数据Fig.1 R-D-T three-dimensional data

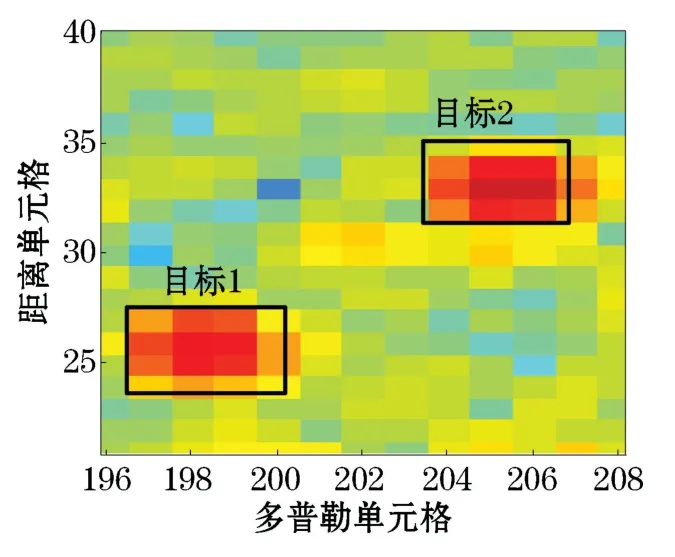
图2 RD谱两个展宽目标Fig.2 RD spectrum of two broadening targets

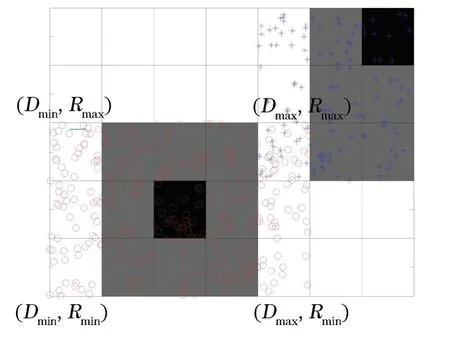
图3 粒子初始化Fig.3 Particle initialization

结合高频地波雷达实测数据、目标特性及粒子滤波探测的原理,总结出了基于粒子滤波的地波雷达目标检测与跟踪联合处理的流程,整个流程共分为5个步骤:第一步,利用多帧RD数据构建R-D-T三维数据;第二步,预处理,主要包括杂波抑制和低门限CFAR处理,对构建的R-D-T数据中每一帧RD谱数据进行预处理,通过预处理可以筛选出主要的目标区,剔掉明显非目标的信息,从而节约计算资源,提高算法效率;第三步,利用基于粒子滤波的方法提取出目标无向航迹;第四步,估计目标航迹的参数,主要是实现目标无向航迹的测向、精确的距离和速度估计;第五步,目标航迹空间定位,即将精确参数估计后的目标航迹由距离-多普勒坐标系投影到地理坐标系,估计其经纬度坐标,完成目标航迹定位(图4)。

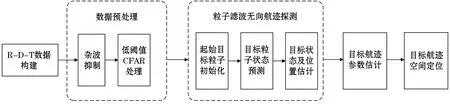
图4 基于粒子滤波的地波雷达检测与跟踪联合处理流程Fig.4 Integrated detection process of high frequency surface wave radar detection and tracking based on particle filter

在完成数据预处理并得到疑似面目标后,记k时刻疑似面目标集合为N k}。对集合内的面目标进行分区处理,使得每一个分区对应一个面目标,然后采用粒子滤波法实现对每一个疑似面目标的无向航迹探测。在整个流程中,基于粒子滤波的无向航迹探测过程最为关键,这个过程又可细分为3步。

1)步骤1:起始目标的粒子初始化。设k时刻某一面目标状态向量为X k=[r k,v k,a k,A k]T,其中r k,v k,a k和A k分别对应k时刻该目标的距离、速度、加速度和幅度四种状态信息。在距离[Rmin,Rmax]、多普勒[Dmin,Dmax]的采样范围内按照x n0～q b(x k)(x n0表示初始化过程中的第n个粒子状态,q b(·)表示采样函数)采样N个粒子。

3)步骤3:目标状态估计。完成粒子的状态转移之后,结合地波雷达目标观测模型来构造检测似然比,计算粒子的权重,第k帧观测数据的未归一化粒子权重可用似然比函数近似表示为

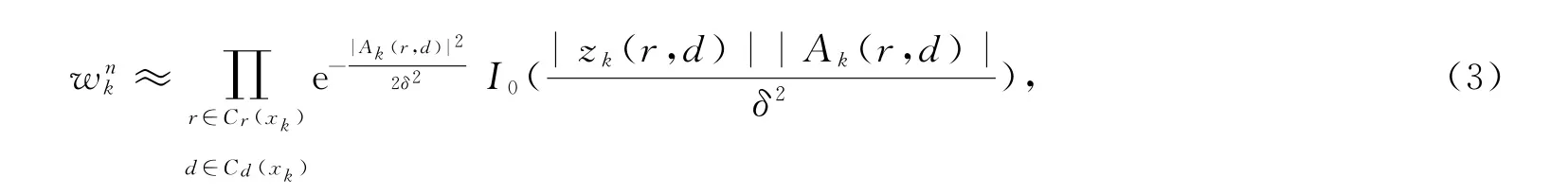
式中,r和d分别为x k在测量数据中对应的距离单元和多普勒单元坐标;C r(x k)={r-q,…,r-1,r,r+1,…,r+q},C d(x k)={d-p,…,d-1,d,d+1,…,d+p};p和q分别为受目标点影响的距离单元和多普勒单元数目;A k(r,d)为目标在(r,d)处的回波幅度;I0(·)为零阶修正的贝塞尔函数;z k(r,d)为第k帧目标在(r,d)处的量测;δ为粒子权重。

比较由式(3)得到的粒子权重与所设置阈值η,当粒子权重大于设置的阈值时,则判断目标存在,然后对所有粒子进行系统重采样,并依据估计目标状态。若连续3帧该目标的粒子权重均小于设置的阈值η,则判断目标消失,终止航迹跟踪。重复步骤2和步骤3,对所有目标进行检测与跟踪处理,得到目标无向航迹集合。

1.3 粒子数自适应确定

理论上,当采样的粒子个数N k足够大的时候,粒子的分布函数就可以表示目标的真实后验概率密度,表示为

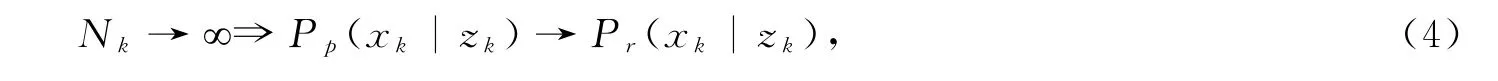
式中,P p(x k|z k)表示采样的N k个粒子集合的概率密度,P r(x k|z k)表示k时刻目标的真实后验概率密度。

一般情况下,地波雷达回波信号中背景噪声复杂、目标信噪比强弱差别较大。对于背景噪声相对均匀且目标信噪比高的情况,只需要少量的粒子就可以满足系统的跟踪需求;对于复杂的背景环境,目标信噪比较低,为了保证跟踪精度,通常需要的粒子数目较大,而粒子滤波算法的复杂度与采样的粒子个数成正比。显然,采用固定个数的粒子不符合实际需求,因此,需要根据目标所处环境对粒子个数进行自适应选取。由于雷达目标存在地波展宽现象,其面目标的粒子权重大小反映粒子拟合目标真实状态程度的高低,因此,通过设置固定的粒子权重之和进行粒子自适应的选取。除此之外,还需确定粒子的最大数目和最小数目。由于在目标消失或者目标信噪比过低的情况下,粒子权重之和需要大量的粒子才能达到设定的阈值,所以,设置最大粒子数目Nmax以避免大量无效计算,设置粒子个数下限Nmin以防止由于信噪比过高导致自适应选取后的粒子多样性损失严重,造成目标跟踪性能恶化或者丢失等情况。自适应粒子滤波步骤为4步。

1)步骤1:粒子初始化。初始化粒子跟踪参数n i=0,S i=0;其中n i表示k时刻第i个目标的粒子数,S i表示k时刻第i个目标对应的粒子权重之和。按照起始目标的先验信息,对目标进行采样,并更新采样的粒子数目。

3)步骤3:粒子自适应选取。当粒子个数小于Nmin或者当粒子个数大于Nmin且小于Nmax但粒子权重和S i小于设定的阈值η时,即满足公式N＜Nmin或(Nmin＜N＜Nmax且S i＜η),需要继续采样粒子;其他情况下,均停止采样。

3 实测数据验证

采用2015年1月在渤、黄海海域开展的地波雷达目标探测实验数据,验证本文提出的基于自适应粒子滤波的地波雷达目标检测与跟踪联合处理方法。雷达工作中心频率为4.7 MHz,距离分辨率为2.5 km,接收阵元数为8个,相干积累时间为262.144 s。其中选用60帧RD谱来构建R-D-T数据,相邻两帧之间的时间间隔为60 s。为了验证本文算法的目标跟踪效果,采用船舶自动识别系统(Automatic Identification System,AIS)航迹数据作为目标真实航迹。

应用基于粒子滤波的检测与跟踪联合处理方法得到航迹跟踪结果,其三维空间分布(图6),基本符合船只目标的运动规律。为进一步分析将其投影到地理坐标系并与AIS结果进行比对,结果如图7所示。可以看出,PF-TBD算法跟踪得到的航迹结果与AIS航迹结果在经纬度上的分布基本一致,结果匹配较好。

为详细比对分析探测结果,分别采用粒子滤波方法和动态规划方法进行了目标检测与跟踪联合处理(图8和图9)。由图8和图9可知,PF-TBD算法和DP-TBD算法的跟踪结果显示其径向距离和速度误差分布相差较大。其中PF-TBD算法得到的航迹与AIS航迹误差较小,径向距离误差小于1 km,径向速度误差小于0.5 km/h,均在地波雷达系统目标探测允许的误差范围之内;而DP-TBD得到的航迹中,其中在前5 min与AIS的径向距离误差大于5 km,径向速度误差在前3 min也大于1 km/h,均超出了地波雷达系统目标探测精度。因此,依据DP-TBD算法得到的结果,可判断出与同步AIS均在较大误差的航迹为虚假航迹,而在判别与剔除虚假航迹方面,PF-TBD算法的结果优于DP-TBD算法。

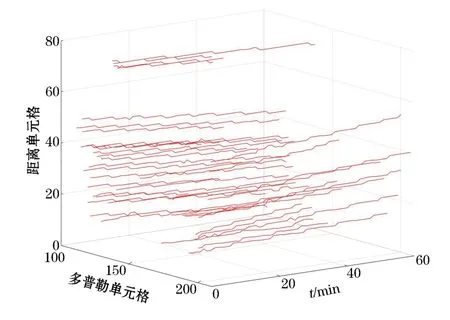
图6 无向航迹跟踪结果三维显示Fig.6 Three-dimensional display of undirected track tracking results

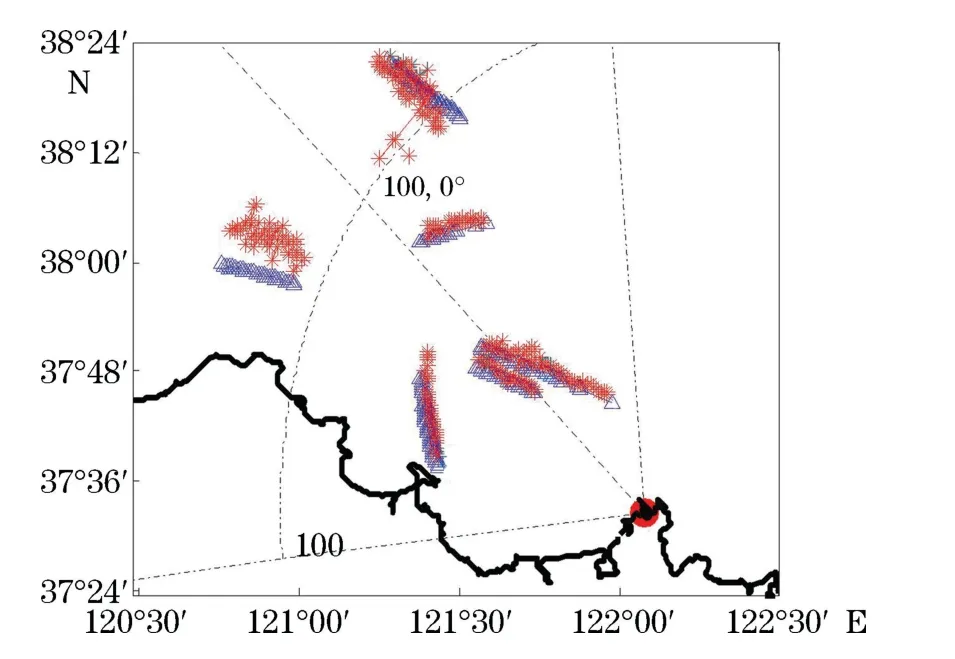
图7 地理坐标系下航迹跟踪结果Fig.7 Tracking results in the geographic coordinate system

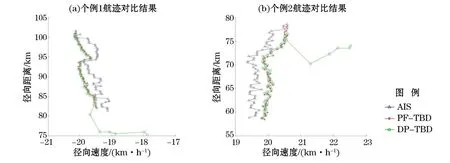
图8 个例1和个例23种航迹对比结果Fig.8 Comparison results of three tracks in two cases

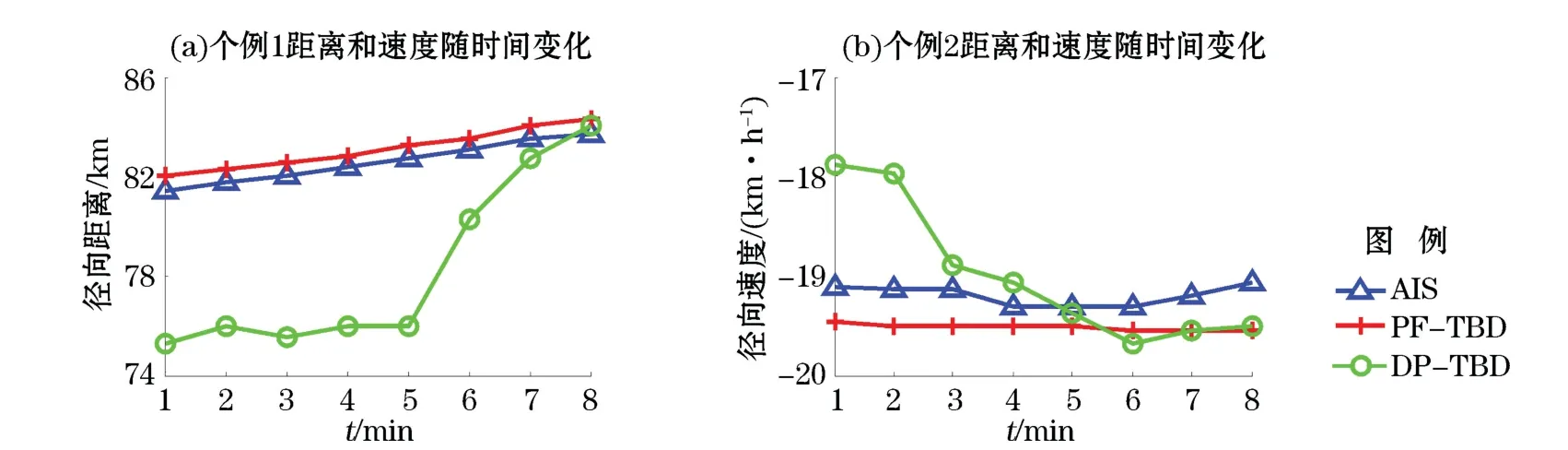
图9 距离和速度分别随时间变化Fig.9 Distance and speed change over time

为了验证结果的可靠性,本文分析了个例1和个例2前7个时刻2种方法得到的目标航迹以及同步AIS航迹的距离和速度随时间变化的分布图(图9)。由图9a可知,从第5分钟到第6分钟,DP-TBD算法得到的目标航迹中距离变化量为4 km,这与根据s=vt计算得出的0.32 km的距离变化量明显不符,因此可判断这个结果属于错误的虚假航迹关联结果。之所以出现这样的现象,原因在于DP-TBD算法是通过设定搜索范围来寻找搜索范围内回波信号强度最大的位置,由于前5 min内的信噪比低(3～5 dB),直接导致DPTBD算法中出现了错误的关联结果;而PF-TBD算法是根据粒子运动状态转移方程来预测目标下一步的位置和状态,对于不符合目标运动规律的噪声点无法通过时间累积能量来形成虚假的目标航迹。因此,PFTBD算法可以在跟踪阶段有效剔除虚假航迹。

自适应粒子数PF-TBD和PF-TBD算法的跟踪整体结果如图10所示。从2种算法跟踪得到的航迹与AIS真实航迹对比可以看到,自适应粒子数PF-TBD算法与PF-TBD算法在大部分情况下跟踪结果一致。但对于个别目标,自适应粒子数PF-TBD算法优于PF-TBD算法,为了验证算法的可靠性,本文给出了目标个例2种方法得到的目标航迹以及同步AIS航迹的结果。

由图11可以看出,自适应粒子数PF-TBD跟踪得到了标号为5的航迹,而PF-TBD未跟踪得到。统计该航迹各个时刻速度,计算得到该目标的平均加速度大小为9.6 km/h2,最大加速度为12.9 km/h2。相对于其他速度变化较慢的船只目标,该船只的速度变化较快,而自适应粒子数PF-TBD方法可通过自适应增加粒子个数,实现对速度变化较快的目标航迹跟踪。

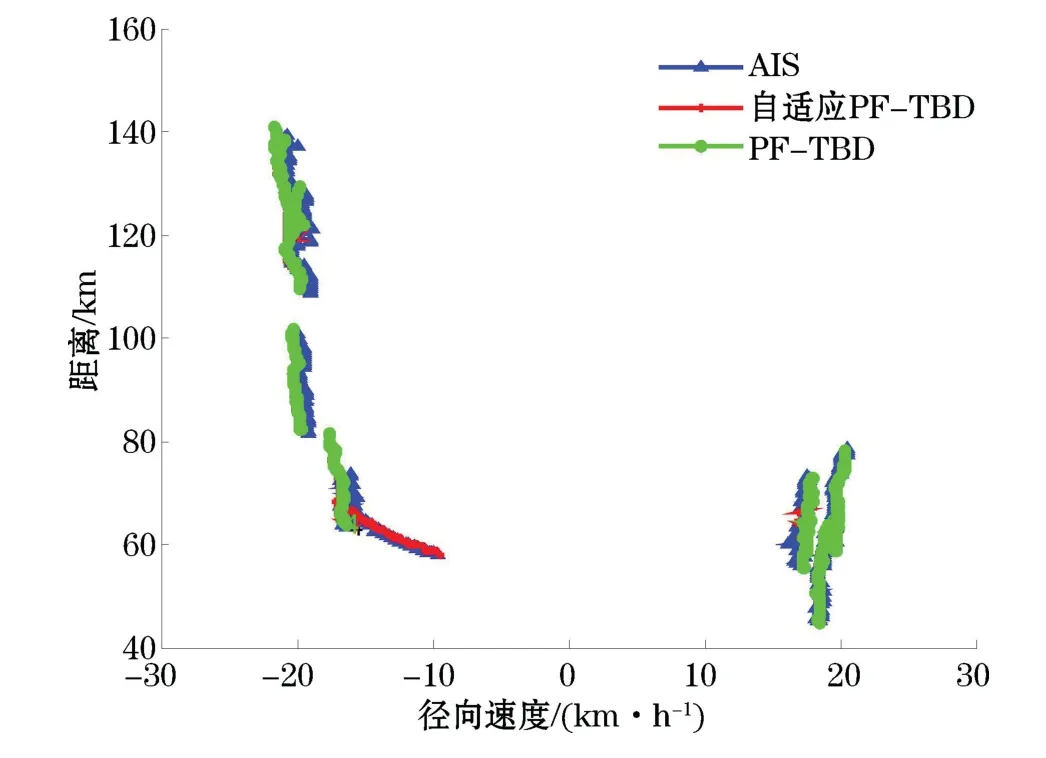
图10 目标AIS航迹与两种算法跟踪航迹整体结果Fig.10 Target AIS track and overall track tracking results of the two algorithms

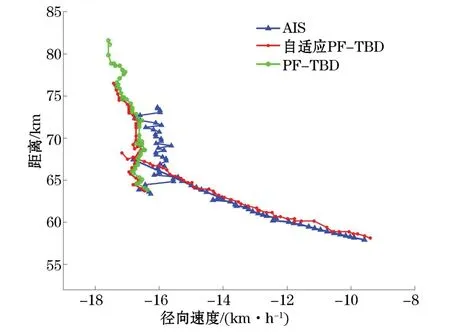
图11 自适应PF-TBD航迹与AIS航迹对比结果Fig.11 Comparison between adaptive PF-TBD track and AIS track

4 结 语

利用地波雷达回波谱数据中运动目标的展宽特性,本文提出了基于自适应粒子滤波的地波雷达目标检测与跟踪联合处理方法,用来解决固定粒子数滤波算法在复杂环境下对弱目标跟踪性能不佳的问题。首先在分析波雷达回波谱数据目标特性基础上,将粒子滤波法应用于地波雷达目标跟踪,提出了基于粒子滤波的地波雷达目标检测与跟踪联合处理的方法;然后,基于目标所处环境实现粒子个数的确定原则和步骤;最后利用2015年实测地波雷达目标探测结果与同步AIS数据来检验方法的有效性,开展了目标检测与跟踪联合处理方法和动态规划方法结果的比较分析。结果表明:本文提出的自适应粒子滤波的地波雷达目标检测与跟踪联合处理方法可实现对速度变化较快的船只目标的有效跟踪,并可排除因某些噪声造成的虚假航迹,整体上提高地波雷达目标航迹跟踪性能。