个人基金投资组合策略实证研究——以5种混合型基金为例

刘知奕

（辽宁科技大学工商管理学院，辽宁 鞍山 114051）

1. 引言

随着2020年全面建成小康社会的总体目标基本实现，人民生活水平和经济条件得到了改善，人均GDP达到了10276美元，人均收入比2010年多了一倍，同时从2011年开始到2019年结束，人均可支配收入累计增长96.6%。个人收入的不断提升，使得投资者储蓄资金不断增多，储蓄资金的提高为投资者带来更自由的资金分配权力，为了使资金带来最大化的收益，投资者逐渐减少储蓄资金，开始注重资产的增值。现阶段，普通投资者选择最多的理财产品包括储蓄、股票、基金、债券、保险等，而受制于储蓄投资的低收益、股票投资的高风险及债券和保险投资的长周期，基金产品逐渐成为投资者的主要选择方向。

刘骏斌等（2018）[1]以十年的普通股票型开放基金和偏股混合型开放式基金为样本，构建有向加权的投资组合重叠网络，并将Fama-French五因子模型引入网络效应，研究结果有利于人们对金融机构的市场行为进行理解；金颖（2014）[2]采用CAPM模型对我国社保基金的投资组合风险进行预测，给出社保基金监管与信息披露的相关建议；张彪（2016）[3]基于有效投资组合理论，给出个人投资理财最大化的方法，对个人理财投资起到借鉴作用；王小华（2012）[4]从投资组合最优化的角度出发，探究我国社保基金在运营方面的问题，并从风险和收益的角度出发，给出最有的投资组合模型。综上，我国学者多将研究对象聚焦到社保基金的投资组合策略，通过实证分析建立投资组合模型，给出投资建议，鲜有学者将研究角度放在个人理财投资组合策略上。

本文以5种混合型基金为例，将个人基金投资收益最大化作为研究目的，构建投资组合模型，最终给出投资组合策略。在此之前，提出如下假设，限定投资收益至少达到20%以及15%，且存在一笔固定资金全部投入到此5种混合型基金中去。

2. 研究设计

2.1 研究机理

混合型基金的投资存在一定的投资风险，因此可将其作为一个随机变量，并可以用收益率的期望来表示混合型基金投资的收益；由于投资收益的不确定性所带来的风险，则可以用收益的方差来表示，那么风险与方差则成正相关。同时，一支基金的平均收益可以用该基金的收益期望均值进行衡量，其波动的幅度可以用收益期望的方差来表示，方差与波动幅度呈正相关，波动越大说明该基金收益越不稳定。而两支基金收益期望间的协方差则表示两者的相关程度，当协方差为0时，说明两支基金不相关；当协方差为正则表示两支基金呈正相关，说明两支基金搭配可以同时赚钱或同时赔钱；当协方差为负则表示两支基金呈负相关，说明两支基金中只有一支可以赚钱而另一支赔钱。

本文用 R1、R2、R3、R4、R5分别表示基金 A、B、C、D、E的月收益率，则Ri（i=1，2，3，4，5）是一个随机变量，随机变量的期望用E来表示，随机变量的方差用D来表示，随机变量的协方差用cov来表示。

2.2 模型建立

本文用决策变量x1、x2、x3、x4、x5分别表示投资者对5种混合型基金A、B、C、D、E的投资比例，假设该投资者要将全部资金投入到以上5种混合型基金中去，则有：

投资者的年期望收益率为：

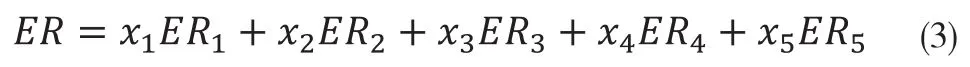
月收益率的方差为：

在实际的投资选择中，投资者可能会面临市场波动、社会因素等方面的影响，并且可供选择的投资方式也更加多样化，同时股票累投资虽然能带来高收益，但是也面临较大的风险，而储蓄投资虽然风险较低，但收益也比较少，因此本文排除其他因素的干扰，只考虑对所选择的5种混合型基金进行投资并且月收益的期望不低于20%，即：

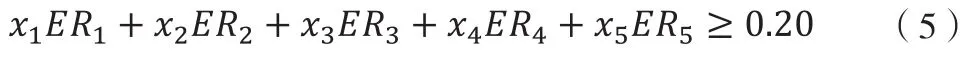
在约束了上式（1）（2）和（5）的前提下，要想得到收益率最大且面临的风险最低，则需要使式（4）最小。

3.个人基金投资组合分析

3.1 5种混合型基金选择合理性分析

优势基金的选择方式有很多，在约束短期投资和长期投资的前提下，可以根据平均收益率或最大收益率的方式筛选。而对于普通投资者来说，在不具备专业知识以及长期分析的前提下，银行理财人员的建议则尤为重要，大多数普通投资者会选择银行理财人员推荐的基金产品进行投资。因此，本文利用专家德尔菲法，选取20名理财专家对目前市场中的混合型基金产品进行打分，最终评选出排名前五的混合型基金，进行投资组合策略分析，在此之前，需要对专家打分结果进行信度分析，即打分结果的合理性分析。

首先对专家的打分进行个案处理，如表1所示，未排除任何基金项目，说明选择基本合理，无缺失值。

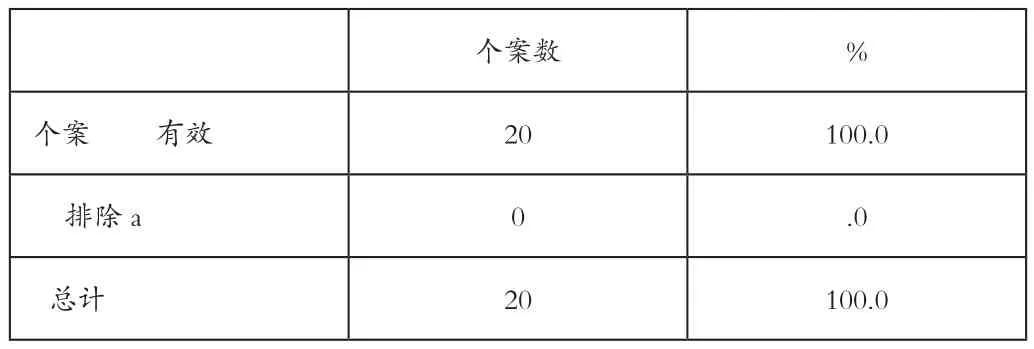
表1 个案处理摘要

再对样本进行可靠性分析，如表2所示，样本的克隆巴赫Alpha系数为0.948＞0.9，量表整体的可靠性极好，可以进行推广并使用。

表2 可靠性统计

随后进行敏感性分析，着重参考“删除项后的克隆巴赫Alpha系数”一项，本量表从上至下所有的Alpha系数相差不大，说明题项设置较好，一致性较高。最后对折半后的相关数据进行观测，如表3所示，折半为不等长，因此观测不等长斯皮尔曼-布朗系数为0.967，因此，本量表的可靠性极高，说明专家所选取的5种混合型基金符合收益强势要求，适合投资者进行投资组合的需求，可以进行进一步研究。

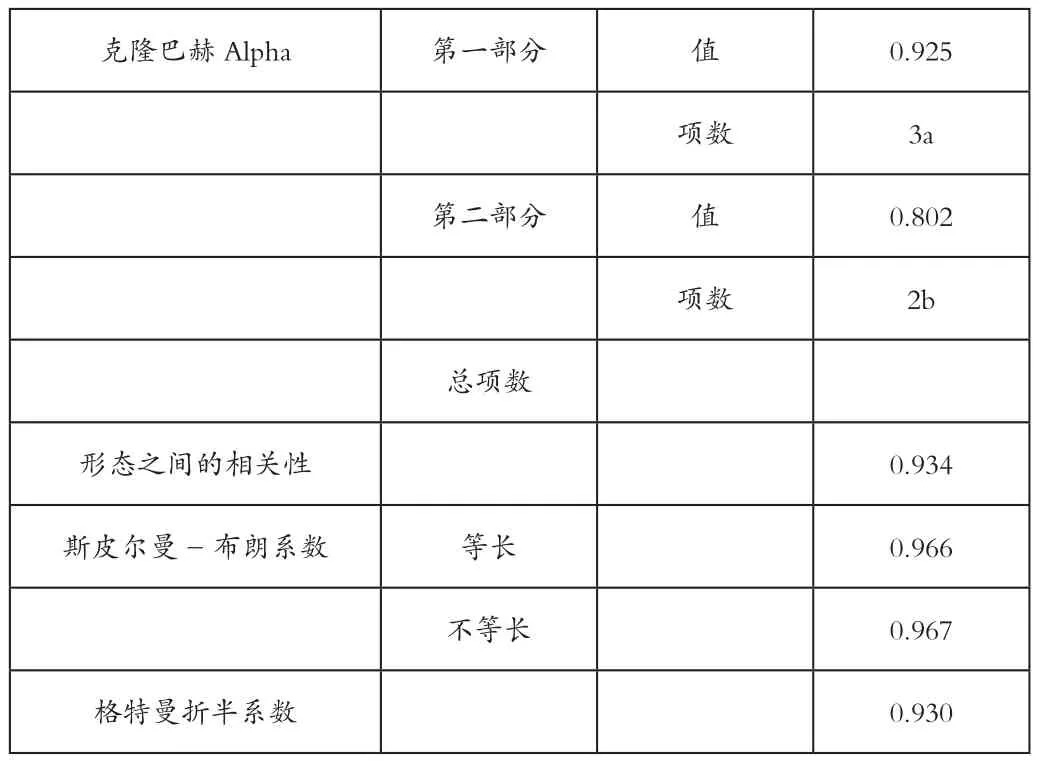
表3 可靠性统计

a项为：A，B，C

b项为：C，D，E

3.2 投资组合分析

通过上述研究，可以得到专家对5种混合型基金的筛选较为可靠的结果，且都具备较好的增长态势，因此投资者可以对以上5种混合型基金的投资进行组合选择。首先，将这5种混合型基金的月收益作为指标，求出其月收益率的期望分别为：

ER1=1.328911，ER2=1.342422，ER3=1.330065，ER4=1.353110，ER5=1.318803

在对其月收益率的协方差矩阵进行求解，结果为：

即 DR1=cov(R1,R1)=0.1196,DR2=cov(R2,R2)=0.1051……DR5=cov(R5,R5)=0.3050，将以上数据带入到投资组合模型中，最终得到第一种假设的结果，即预期的投资收益率为20%，投资5种混合型基金的比例为A、B、C三种基金均不投资，投资D基金的比例为94.2%，投资E基金的比例为5.8%，该组合的风险为0.115。如果对第二种假设进行验证，即降低收益率为15%，则得到的结果不变，仍为上述的投资比例。

4.结论

本文首先对市场中混合型基金利用专家德尔菲法进行综合排名，选取排名靠前的5种混合型基金作为研究对象，随后通过信度检验验证了打分结果的可靠性，进一步将5种混合型基金的月收益作为研究指标，将其收益率期望和协方差矩阵带入到投资组合模型中，得到适合的投资组合比例。

研究发现，在给定预期收益的情况下，达到收益率为20%，需要对第4种D基金大量投入，为降低风险，再少量投入E基金，而A、B、C基金受风险和收益的影响，应避免投资；在降低预期收益重新计算投资比例，结果显示投资比例未有变动，无论预期收益调高或调低，投资的比例完全不变，只有投资风险发生改变，符合经济学中“分离定理”，结论得到验证。