Heston模型在我国期权市场中的应用

陈 科，李砚涵

（广州大学松田学院，广东 广州 510000）

1.引言

1973年，布莱克、斯科尔斯和莫顿提出了著名的Black-Scho les（Black-Scholes-Merton）期权定价模型。该模型中的参数包括标的资产价格，无风险利率，期权执行价格，到期期限和标的资产价格波动率，这些参数要么在市场中可直接观测到，要么可以通过市场数据计算，这使得B-S公式在实际应用中得到了极大的推广，而布莱克和斯科尔斯也因此获得了1997年的诺贝尔奖。

B-S模型对期权定价有以下7个主要假设：一是股票价格服从对数正态分布，且均值μ、标准差σ均为常数；二是允许卖空；三是无交易成本；四是在期权的有效期内无分红；五是没有无风险套利机会；六是证券交易是连续的；七是对所有到期日的期权，无风险利率r为一相同的常数。正是由于这些严格的假定，使得B-S模型与实际的期权市场会存在着系统性的偏差，例如真实市场上股票价格并非B-S模型中所描述的对数正态分布，而是呈现出尖峰厚尾的特征。又如BSM 模型所要求的波动率为恒定的假设在实际的金融市场上并不成立，实际上是存在着波动率微笑曲线。

针对B-S期权定价模型的不足，研究者对该模型提出了各种改进，其中一类改进的方向就是不再假设标的资产的波动率为常数，而是对其波动率建立动态模型，也即随机波动模型（SV模型），在众多的SV模型中，Heston模型应存在闭形式解而优于其它模型，这也是本文选择Heston模型对我国期权进行研究的原因。

关于股票价格和波动率的运动过程，Heston给出的模型如下：

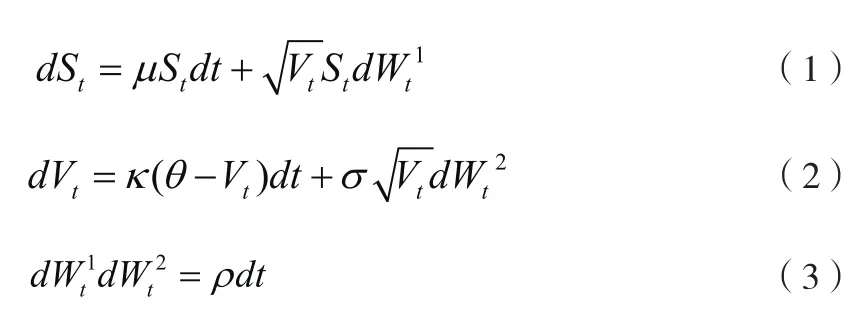
其中，St表示t时刻股票价格；μ表示股票价格的均值；Vt表示t时刻股票价格的方差；是相关的布朗运动，相关系数是ρ。

Heston（1993）提出上述模型中欧式看涨期权的价格满偏微分方程：

其中λ(St,Vt,t)被称为波动率的价格，是一个不可观测量，Heston假定λ(St,Vt,t)正比于波动率，即

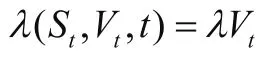
其中λ为常数。

Heston指出（4）的解具有和BS模型类似的形式：

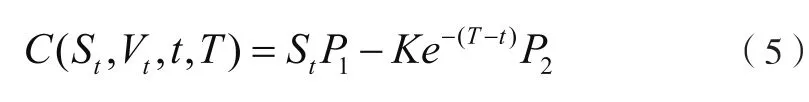
通过将（5）式代入（4）式，Heston解出P1和P2如下：

2.Heston模型

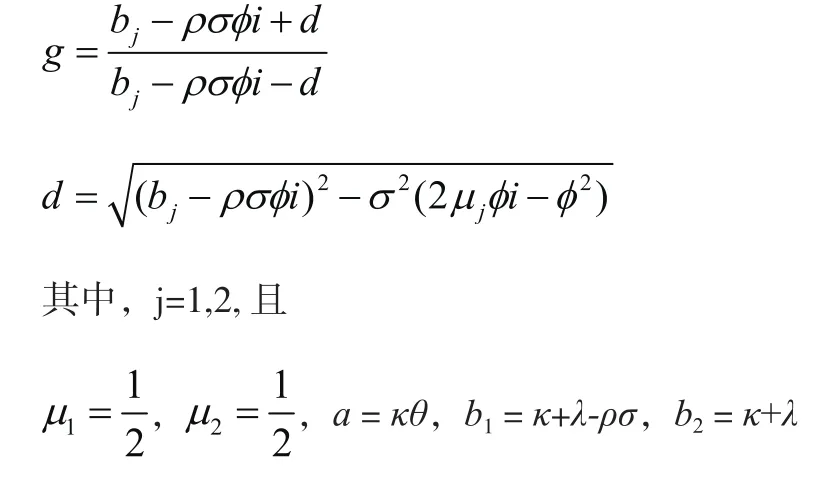
在上式中λ是波动率风险的市场价格，由于波动率并非实际市场上存在的可交易商品，故λ不易获得。但可以通过等价鞅测度在风险中性世界消除λ。在风险中性测度Q下，标的资产的动态方程变为：

上式中CP为真实世界中的看涨期权价格，CQ为风险中性世界中的看涨期权价格，在其中为波动率风险市场价格为0。

3.Heston模型校准

Heston模型中包含多个未知参数需要进行估计，原Heston模型中有六个待估参数κ，θ，σ，Vt，ρ，λ。通过等价鞅测度Q的转化，在风险中性世界中模型含5个参数κ*，θ*，σ，Vt，ρ。本文将在风险中性世界对模型的参数进行估计，此时所需要估计的参数集合本文的估计方法是要使得模型求解的期权价格和市场价格的误差最小，也即要求解如下的非线性最小二乘问题：

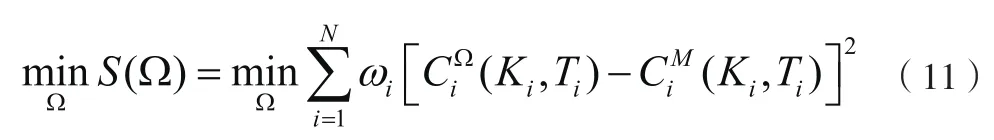
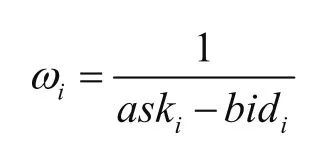
对于（11）式的非线性最优化问题，本文将采用模拟退火算法进行求解。

4.Heston模型实证研究：基于50ETF指数期权

4.1 数据处理

本文采用上证50ETF指数欧式看涨期权在2020年10月27日的数据（数据来源：聚宽量化交易平台），样本包含了到期日为2020年11月25日和2020年12月23日的期权，其中2020年11月25日到期期权执行价格包含2.95、3、3.1、3.2、3.3、3.4、3.5、3.6、3.7、3.8共10个点位，2020年12月23日到期期权执行价格包含2.55、2.6、2.65、2.7、2.75、2.8、2.85、2.9、2.95、3、3.1、3.2、3.3、3.4、3.5、3.6、3.7、3.8、3.9 共 19 个点位，本文共选取了29个期权样本数据。本文研究期间各大银行存款年利率为1.5%，但市场上存在的各种无风险理财产品的年利率都在2%以上，所以本文选取无风险利率为2%。本文对各支期权选取的买价bid和卖价ask，分别为该期权在2020年10月27日这一天的tick级bid和ask数据的平均，而期权价格则取为bid和ask的平均值。为了数据的一致性，表的资产50ETF的价格也取为其在当天tick级数据的平均值，该平均值为3.344。

4.2 实验结果

给定初始值 [κ*，θ*，σ，ρ，Vt]=[0.0462，0.999，0.248，0，0.0897]，在此初始取值下目标函数S(Ω)的取值为58.992。

通过模拟退火算法，迭代搜索目标函数S(Ω)的最小值，得到优化之后的解为

[κ*，θ*，σ，ρ，Vt]=[0.1389，0.3021，0.2027，0.5068，0.0404]

在这一组参数取值之下，目标函数S(Ω)的取值为1.5797.迭代优化的过程由下图所示：

图1 模拟退火算法参数优化过程

4.3 模型外推检验

为了验证该模型的有效性，在参数 [κ*，θ*，σ，ρ，Vt]=[0.1389，0.3021，0.2027，0.5068，0.0404]下将该模型应用于2020年10月28日这一天的定价，该天标的资产50ETF的tick级数据平均值经计算取值为3.3545元，仍然选取上文所提到的29支期权，经模型计算并与实际的市场数据进行比较。结果如表1：

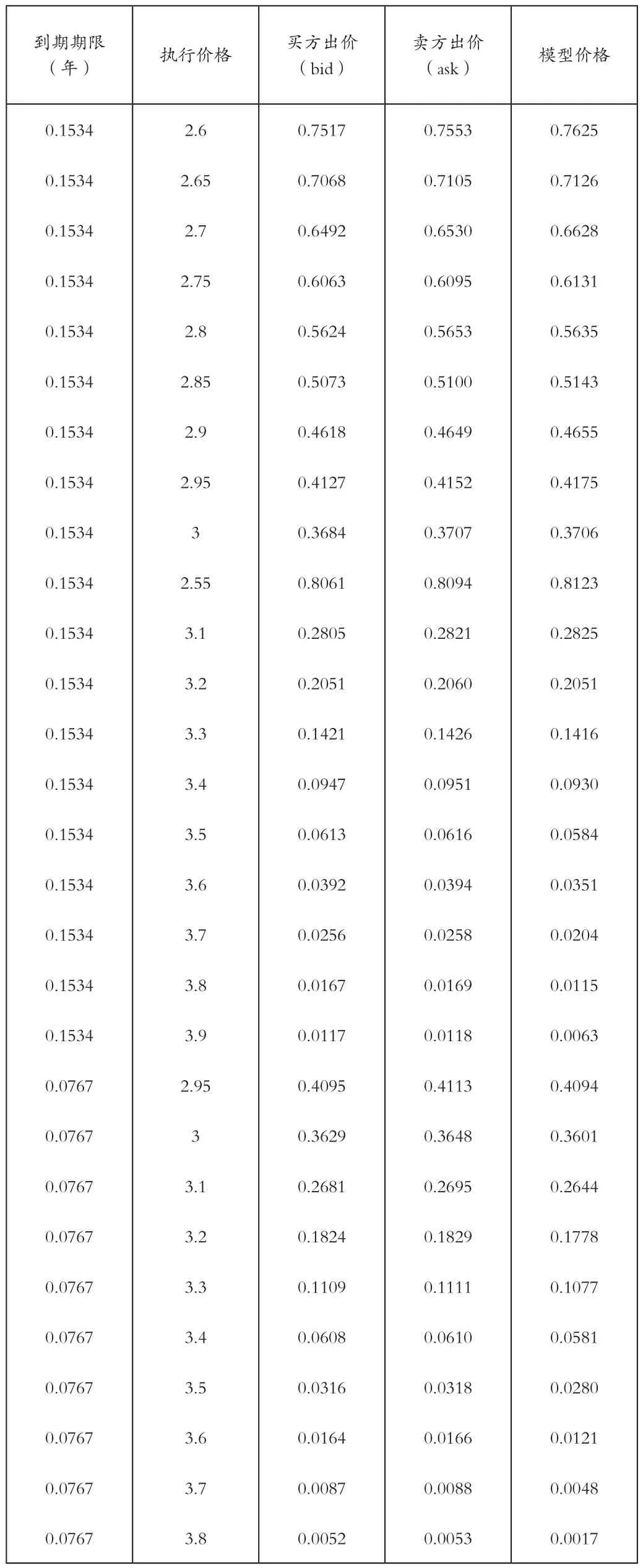
表1 检验结果

从上表可以看出除了个别期权之外，大多数期权的模型计算价格与实际的买价和卖价都很接近，另外重新计算了目标函数的值，S(Ω)此时的取值为1.3504，这也反映出该模型用优化后的参数所计算出来的值与实际值的吻合度较高。

5.结语

本文运用Heston模型对我国期权市场ETF50期权进行了研究，在Heston模型中包含5个位置参数：均值回复速度κ，长期方差θ，波动率方差σ，相关系数ρ，初始方差V，本文通过设置目标函数S(Ω)，然后以迭代寻忧的方式求得了该模型的最优参数，最优在该参数下对第二天的期权价格进行计算并与实际价格进行比较，发现在这一组参数下模型值与实际值吻合程度较好。

在求解模型中设置的目标函数S(Ω)是其参数的多元非线性函数，并且存在很多局部极小值，因而参数优化过程受到初始设置的很大影响，很有可能会收敛到局部极小值。如何利用人工智能进行全局最优化，将是进一步研究的方向。