空间柔性闭链机器人动力学建模与振动仿真
2021-02-01张青云赵新华戴腾达
张青云 赵新华, 刘 凉 戴腾达
(1.天津理工大学计算机科学与工程学院, 天津 300384;2.天津理工大学天津市先进机电系统设计与智能控制重点实验室, 天津 300384)
0 引言
并联机构因承载力强、结构刚度大、累计误差小等特点[1-4]而广泛应用于机器人、航天、工业制造等领域。为了减少系统能耗、提高效率,闭链机器人一般由细长连杆构成,导致系统构件在运行过程中柔度增加、固有频率降低、弹性振动变大,从而影响了系统稳定性及轨迹运行精度。目前,对并联机构的振动分析主要集中在残余振动方面,很少涉及系统自激振动。文献[5]对物料装填机器人末端的残余振动进行了分析和抑制。文献[6]采用应变率反馈控制方法抑制了3-RRR平面柔性并联机器人残余振动。文献[7]建立了刚柔热耦合的旋转中心刚体-功能梯度材料梁的动力学模型。文献[8]通过S形曲线对机器人残余振动进行研究。文献[9]对Delta并联机器人残余振动进行控制分析。文献[10]对伸缩臂进行了抖动抑制研究。文献[11]采用主动控制方法对平面3-RRR柔性并联机器人的自激振动进行有效抑制。文献[12]采用非线性PD和模糊控制算法对3-RRR平面柔性并联机器人自激振动进行了分析。文献[13]对平面3自由度并联机器人的自激振动进行了控制研究。上述研究主要针对柔性臂和平面柔性机构的自激振动进行分析,鲜有涉及空间柔性闭链机构的自激振动。文献[14]建立了3-RRS柔性空间并联机器人的动力学模型,并对系统固有频率进行分析,但运动支链中不存在空间柔性构件。文献[15]对含柔性连杆的并联机器人动力学方程进行数值分析。文献[16]建立了含多个柔性连杆和柔性铰的空间全柔性机器人动力学模型,但并未对空间柔性系统的振动特性进行分析。
为了实现低成本、高效的振动特性分析,通过仿真技术对系统振动效应进行研究也逐渐趋于成熟。文献[17]对天平包装件的随机振动进行了振动仿真分析,并对该机构进行优化设计。文献[18]建立了一种5自由度喷涂机器人运动学模型,并对系统振动模型进行了受迫振动分析。文献[19]通过采用ADAMS /Vibration对钢管自动输送机构进行了振动仿真分析。文献[20]通过多体动力学软件对定轴齿轮箱刚柔耦合模型的振动频率特征进行分析。文献[21-23]通过仿真方法验证了并联机器人动力学模型的正确性。文献[24]建立了轮式车辆传动系的自激扭转振动仿真模型。
本文采用有限单元法对柔性构件进行离散,利用浮动坐标系法构建连杆位移场,最后通过Lagrange方程建立空间刚柔耦合闭链机器人的动力学模型及振动方程,并对系统固有频率和振型函数进行数值求解。在同等参数条件下,利用ADAMS/Vibration模块建立空间刚柔耦合闭链机器人的振动仿真模型,对其进行自激振动分析,研究系统固有频率和对应模态的变化,以及不同激振力作用下的频率响应特征。
1 动力学模型
1.1 物理模型
空间柔性闭链机器人结构简图如图1所示,它由静平台、动平台及3条三角对称的运动支链AiBiCiPi(i=1、2、3)构成。其中,Ai、Bi、Ci为旋转关节连接点,Pi为虎克铰关节连接点。由于连杆CiPi(i=1、2、3)为细长构件,系统高速运行下将产生柔性变形,导致振动增强,从而影响系统稳定性。因此,对系统进行动力学及振动特性分析时,需将其设为柔性构件,而连杆AiBi、BiCi(i=1、2、3)和动平台则设为刚性构件。
运动支链的坐标系简图如图2所示。其中,全局坐标系OXYZ和局部坐标系Pxyz设在静平台和动平台的几何中心,其余连杆坐标系则设置在各连杆的上关节处。φi为支链坐标系AixAiyAizAi中x轴与全局坐标系X轴之间的夹角,θi1、θi2和θi3为连杆坐标系下各连杆与转轴之间的夹角,并且连杆AiBi、BiCi绕局部坐标轴y转动,而连杆CiPi则绕z轴转动,因此,柔性连杆CiPi为空间构件。
1.2 空间柔性连杆运动学描述
空间柔性连杆坐标系固定在构件端点处,可简化绝对运动描述。基于浮动坐标系,空间柔性连杆上任意点w在全局坐标系下位移矢量可表示为
rw=r0+Rξ
(1)
其中
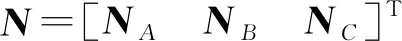
式中r0——柔性连杆坐标系原点在全局坐标系下的位移矢量
ξ0——未变形矢量ξf——变形矢量
qf——单元节点位移向量
N——插值函数
R——柔性连杆坐标系变换到全局坐标系的变化矩阵
NA、NB、NC分别采用线性函数和三次多项式函数进行插值计算。
根据上述描述可知
R=Ri1Ri2Ri3
(2)
式中Ri3——坐标系Pxyz变换到坐标系CixCiyCizCi的变换矩阵
Ri2——坐标系CixCiyCizCi变换到坐标系BixBiyBizBi的变换矩阵
Ri1——坐标系BixBiyBizBi变换到坐标系AixAiyAizAi的变换矩阵
对式(1)求导,可得任意点在全局坐标系下的速度矢量为
(3)
式中I——单位矩阵
n——运动支链i中刚性构件数
同理,全局坐标系下柔性连杆的绝对转角为
(4)
其中
式中O——零矩阵
1.3 空间柔性构件动能
空间柔性构件动能包括平动动能和转动动能,则空间柔性构件的平动动能Tf-T可表示为
(5)
而空间柔性连杆的转动动能Tf-R为
(6)
式中L3——柔性连杆长度
ρ——柔性构件密度
Jc——构件绕质心的转动惯量
Mf-T、Mf-R——对应平动动能和转动动能的质量矩阵
空间柔性连杆总动能为
(7)
式中Mf——空间柔性构件对应的质量矩阵
1.4 空间柔性构件势能
空间柔性构件势能由弹性势能和重力势能构成。其中,空间柔性连杆的弹性势能对应的刚度矩阵可通过虚功原理推导得
(8)
其中
σ=Eεε=Dξf
式中E——弹性模量矩阵
ε——应变位移关系
D——应变-位移的偏微分算子
则空间柔性构件刚度矩阵为
(9)
空间柔性连杆对应的弹性广义力为
Ff=Kfq
(10)
其中
式中On——n个刚体广义坐标对应的刚度矩阵项
q——系统广义坐标
空间柔性构件重力广义力为
(11)
式中m3——柔性连杆质量
rw_z——柔性连杆质心在全局坐标系下Z轴方向坐标值
1.5 空间柔性构件动力学方程
将式(7)~(11)代入Lagrange方程,则空间柔性连杆的动力学方程可表示为
(12)
其中
Qf=QfF-Qfv
式中Qfv——速度二次项
QfF——单元所受广义外力
由于变形矢量ξf是在局部坐标系下进行描述,将其变换到全局坐标系下表示为
ξf=Buf
(13)
式中uf——全局坐标系下的柔性广义坐标
B——全局坐标系AixAiyAizAi变换到局部坐标系CixCiyCizCi的变换矩阵
将式(13)代入式(12),则空间柔性连杆在全局坐标系下表示的动力学方程为
(14)
1.6 运动支链动力学方程
运动支链由空间柔性构件及刚性连杆AiBi、BiCi组成,其中,刚性连杆AiBi、BiCi动能和势能分别为
(15)
(16)
式中m1、m2——连杆AiBi和BiCi质量
L1、L2——连杆AiBi和BiCi长度
vi1、vi2——连杆AiBi和BiCi绝对速度
J2——连杆BiCi转动惯量
ωi2——连杆BiCi转动惯量绝对角速度
1.7 约束关系

P′=P+JPΔP
(17)
式中 ΔP——动平台微小位移
动平台的动力学方程可写为
(18)
式中mP——动平台质量
J——动平台转动惯量
zP′——动平台在全局坐标系Z方向位移
1.8 系统动力学方程
由式(14)~(18)可得到空间柔性闭链机器人动力学方程为
(19)
2 固有频率和振型分析
由式(19)可得空间柔性闭链机器人自由振动方程为
(20)
根据模态分析理论[26]可得系统固有频率和模态振型表达式为
|-λM+K|=0
(21)
当质量矩阵M为非奇异矩阵时,令C=M-1K,则式(21)可改写为
(22)
式中ωm——系统固有角频率
fm——系统固有频率
空间柔性闭链机器人系统参数如表1所示。
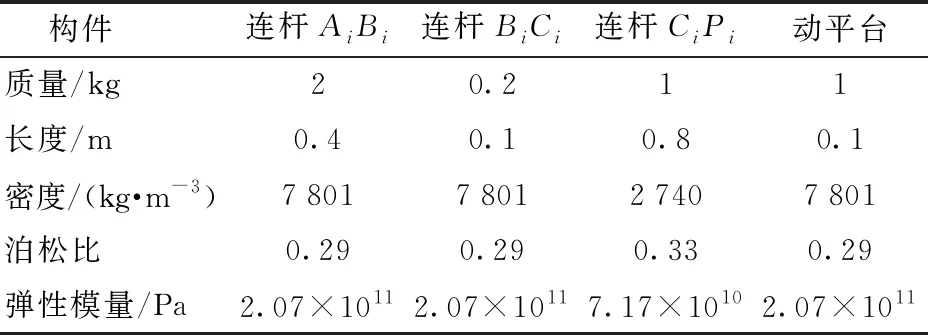
表1 系统参数Tab.1 System parameters
系统动平台几何中心的运动轨迹为
(23)
其中,t=5 s,静平台半径r=0.4 m,角速度ω=2 rad/s。
通过Matlab软件编写程序进行仿真可得空间柔性闭链机器人固有频率随时间变化的关系如图3所示,以及动平台在全局坐标系下随时间变化的运动轨迹如图4所示。
由图4可知,在空间柔性构件的作用下,理论模型的动平台在X方向和Y方向最大浮动值分别为0.008 9 m和0.004 7 m,而Z方向位移在-0.701 2~-0.699 8 m之间波动。
3 振动仿真
基于图1,利用ADAMS软件建立空间柔性闭链机器人的仿真模型。再通过ADAMS/Vibration模块对系统进行约束模态分析。由于系统中的空间柔性杆为均质、圆形截面构件,结构简单,故直接通过Flexible Bodies模块进行柔化处理,产生1 014个节点,2 136个单元。
3.1 自由模态分析
通过振动仿真分析,空间柔性闭链机器人在自由状态时的前12阶固有频率如表2所示。
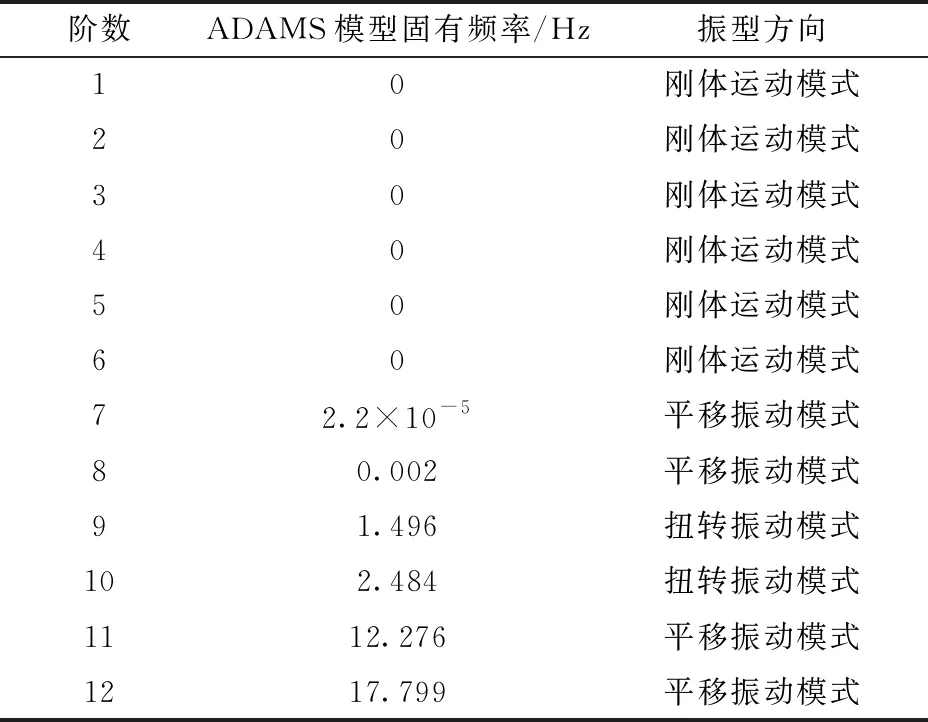
表2 振动仿真模型前12阶固有频率Tab.2 The first 12 natural frequencies of vibration simulation model
由表2可知,ADAMS模型中的前6阶固有频率都为0,即系统对应的刚体模态,它由3个移动模态和3个转动模态构成。因此,系统最小固有频率出现在第7阶,对应固有频率为2.2×10-5Hz。而理论模型通过式(22)计算后,对应系统最小固有频率为4.02×10-5Hz。由于振动仿真系统由多个刚柔构件组成,并且空间柔性构件的单元数多,柔度大,所以仿真模型的最小固有频率小于理论模型,但两者数值基本一致,验证了振动仿真模型建立的正确性。因此,可通过该振动仿真模型对其系统振动特性进行精确仿真分析。
3.2 约束模态分析
为了分析空间柔性闭链机器人实际工作状态下的振动特性,将空间柔性闭链机器人的载荷以质量的形式进行描述(表1)。由于空间柔性构件的变形受到与之相连的刚性构件的影响,因此,将该空间柔性构件边界条件设为两端铰支,而系统其他构件的约束关系则通过Connector模块进行设置,如表3所示。

表3 机构约束关系Tab.3 Constraint relationship
通过对空间柔性闭链机器人进行约束模态分析可知,系统3~12阶固有频率如表4所示。

表4 约束模态系统频率Tab.4 System natural frequency in constrained mode
由表4可知,空间柔性闭链机器人约束模态下的固有频率远大于自由模态下的固有频率,说明系统在约束状态下的系统动力学特性更好也更符合实际工况。因此,通过对系统进行约束模态分析具有实用价值。
而在系统约束状态下,对空间柔性闭链机器人进行动力学仿真可得动平台随时间变化的运动规律如图5所示。
由图5可知,系统动平台在X和Y方向的位移为-0.103 6~0.100 9 m和-0.102 5~0.100 6 m,Z方向的位移运动范围为-0.700 8~-0.699 3 m。通过与理论模型动平台运动轨迹对比可知,两类模型在同等参数条件下的运动轨迹基本一致,验证了理论模型和分析模型建立的正确性。
3.3 自激振动仿真
空间柔性闭链机器人系统高度非线性,系统运行过程中不仅存在空间柔性构件弹性变形引起的振动。同时,空间柔性构件的弹性变形也将引起动平台的微小位移,产生轨迹偏差。此时,为了补偿轨迹偏差,通过系统内部振源进行自身调节而激励的振动则为自激振动。
通过对约束状态下的空间柔性闭链机器人进行自激振动仿真分析可知,系统共有31阶模态,由图6可知模态最大值为25 Hz。
空间柔性闭链机器人主要频率及振型如图7所示。
系统特征值与固有频率如表5所示。

表5 系统特征值与固有频率Tab.5 System natural frequency and characteristic value
为了分析不同激振力对系统振动频率的影响,需要定义系统输入通道和输出通道。其中,输入通道用于设置激励值及其作用位置,输出通道则是对系统的响应频率进行检测。为了对比不同激励对系统振动特性的影响,设置3个不同位置的输入通道,3个输出通道,位置如表6所示。

表6 输入和输出通道参数Tab.6 Input and output channel parameters
系统输入通道采用简谐激励F(t)=f0sin(ωt),则对应不同f0的系统幅频响应曲线如图8所示。
由图8可得,3个激励中,f0=1 000 Hz对应的幅频响应最大,f0=100 Hz次之,而f0=10 Hz的幅频响应最小。当激励作用于空间柔性构件质心xCi方向时,动平台Y方向响应最强,Z方向次之,而X方向最小。当激振力频率在20~60 Hz时,系统幅频响应曲线出现明显跃升和下降,振动效应明显。
当3个不同激励作用于空间柔性构件质心yCi方向时,如图9所示,随着激振力幅值的增加,动平台质心处X、Y、Z方向幅频影响特性也随之增强。其中,最大幅频响应为f0=1 000 Hz时动平台质心处Y方向响应,最小幅频响应值为f0=10 Hz时动平台质心X方向响应。
由图10可知,幅频响应最大值出现在图10b中,而图10a次之,图10c最小。并且激振力幅值越大,幅频响应也越强。
由于低频模态对系统的影响较大,故通过1~100 Hz频段的模态坐标图来分析系统自激振动特性。其中,对应同一激励作用的系统各阶模态参与因子曲线图如图11所示。
通过自激振动仿真可知,系统第11、12阶模态对应系统最大变形,对应激振频率在40~60 Hz之间,并且随着激振频率的逐步增加,系统幅频响应值开始下降,系统趋于稳定。因此,为了能有效抑制系统柔性变形导致的振动问题,应尽量避免外部激励频率为40~60 Hz。
4 结论
(1)建立了考虑空间柔性构件变形的刚柔耦合闭链机器人动力学模型,分析可知,系统空间柔性构件的弹性变形对系统动平台的轨迹精度和振动效应具有重要影响,符合实际工况,可为空间柔性闭链机器人的控制设计提供理论支持。
(2)振动仿真模型和理论模型的固有频率基本一致,验证了振动仿真模型的正确性。因此,可以利用仿真模型对空间柔性闭链机器人进行振动特性分析。
(3)通过自激振动分析得到动平台质心在3个坐标轴方向的幅频响应曲线,结果表明:激振力幅值越大,系统幅频响应越强。其中,Y方向响应最大,X方向次之,Z方向最小。
(4)由各阶模态参与因子曲线图可知,系统第11、12阶模态对应的系统变形最大,对应的激振频率为40~60 Hz。因此,为了有效抑制系统柔性变形而导致的振动问题,应使系统外部激励频率远离该频率范围。
