半对称三平移Delta-CU并联机构运动误差分析与标定

孟庆梅 李佳宇 李 菊 邓嘉鸣 沈惠平

(常州大学现代机构学研究中心， 常州 213164)

0 引言

并联机构比串联机构承载能力强、运行速度快。由于其构件多，存在由制造、装配、杆件变形等引起的误差，导致其执行末端的几何精度降低，直接影响了并联机器人的应用。因此，在实际应用并联机器人的过程中，须进行相应的精度标定，并据此修正并联机构控制模型参数或系统输入。

国内外关于并联机器人误差建模及运动学标定的研究主要借助于自身冗余传感器、激光跟踪仪及三坐标测量仪等设备，从而检测末端位姿信息，计算实际测量值与理论值之间的偏差。唐国宝等[1-2]通过检测沿末端标定坐标系的轴向误差可辨识出全部集合参数，通过检测动平台z轴方向的位置偏差实现对Delta的运动学标定，但需要确定参考坐标系和标定坐标系之间的约束条件。张文昌等[3]以激光跟踪仪作为测量工具，提出一种步进迭代的误差参数辨识方法，完成对Delta机器人的标定。梅江平等[4]采用环路增量法构造了码垛机器人平行四连杆的误差模型,并建立了带关节变量比例系数的运动学误差模型,从而对关节传动误差进行补偿。梅江平等[5]提出一种基于末端转角误差信息的快速零点标定方法，基于机器人单支链闭环矢量方程建立了零点误差全集与末端误差之间的映射模型，构建了机器人的快速零点误差辨识模型。贺礼等[6]在基于D-H变换矩阵导出的运动学方程基础上，建立了Delta机器人线性方程组表示的位姿误差模型。MAURINE[7]用激光位移传感器标定了Delta-4型并联机器人。ZHUANG[8]利用电子经纬仪测量了Stewart平台的位姿误差集。CHIU等[9]利用安装在静平台和动平台之间的可伸缩杆，实现了对Hexapod并联机床的标定。杨启志等[10]针对一种并联式三平移移栽机器人，分析了因动平台质量变化而引起的系统末端机械手误差变化。于今等[11]为提高直线驱动型并联机器人动平台末端执行器位置精度,在灵敏度误差模型的基础上,提出了一种误差源筛选方案,降低了误差参数辨识的复杂程度和计算量,对结构较复杂的机构误差补偿具有一定指导意义。

本文针对一种半对称三平移并联机器人机构Delta-CU(三平移并联机构2-RPa⊕RUU)，提出基于模糊神经网络的误差参数识别模型和误差补偿方法，并进行实验分析与验证。

1 并联机构的误差模型

考虑影响Delta-CU并联机构操作手的误差来源，基于模糊神经网络建立机构误差模型；同时，采用外部直接标定法，利用激光跟踪仪对并联机器人执行末端位姿进行测量；再通过误差补偿方案，分别对并联机器人的末端位姿误差进行补偿。

1.1 Delta-CU并联机构拓扑设计

传统的Delta机构包含3条相同的混合支链，结构较复杂。本文提出一种半对称的并联机构2-RPa⊕RUU，如图1所示[12]，它由静平台0、动平台1，以及2条相同的混合支链HSOC和1条无约束的RSS型支链组成，其中，每条混合支链由1根驱动杆和1个平行四边形4R组成，记作P(4R)，该驱动杆和平行四边形之间通过转动副连接；RSS型支链的两杆之间通过球副连接，该支链与静平台0通过转动副连接，与动平台1通过球副连接。3条支链中与静平台0连接的驱动杆的长度相等，RSS型支链中与动平台1连接的杆长与混合支链中平行四边形的长杆相等。同时，为了避免RSS支链上球副承载力小、限制杆件摆动空间的缺点，采用U副代替S副，即为2-RPa⊕RUU机构。

与Delta相比，该机构具有结构简单、加工装配维修容易等优点。本团队已完成该机构的运动学综合分析、刚度分析和动力学分析[13-15]。

1.2 建立标定坐标系

定义误差模型的标定坐标系为o′x′y′z′。由于激光跟踪仪的测量坐标系OXYZ与标定坐标系o′x′y′z′不同，基于外部直接标定法进行误差标定和补偿时，利用整体最小二乘法[16]求得两坐标系之间的转换参数。

Delta-CU机构的第Ⅰ、Ⅲ条支链如图2所示，为了方便建立机构误差模型，将静平台的坐标系oxyz建立在几何中心点o，y轴指向第Ⅱ支链主动臂转轴中心；坐标系AixAiyAizAi为支链坐标系，yAi与支链中主动臂理想转轴重合，xAi与静平台几何中心点o重合，zAi满足右手螺旋法则。

设空间任意转换点P在两坐标系中的坐标(x′p,y′p,z′p)与(Xp,Yp,Zp)之间的关系为

(1)

其中

R=R(θx)R(θy)R(θz)

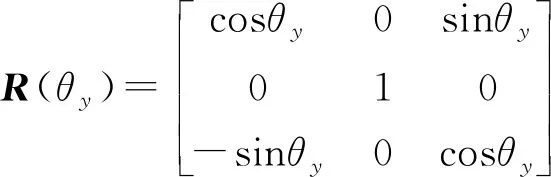
式中k——尺度因子T——平移矩阵

Δx、Δy、Δz——坐标平移参数

R——旋转矩阵

θx、θy、θz——坐标系绕各轴旋转角

令：m1=k+1，m2=m1θx，m3=m1θy，m4=m1θz，θx、θy、θz为微小角，则式(1)可写为

对于n组转换点的坐标转换矩阵可以写为

L=AX

(2)

其中

X=[ΔxΔyΔzm1m2m3m4]T

(3)

L=[L1L2…Ln]T

(4)

L1=[x′1y′1z′1]T

式中A——系数矩阵

X——未知参数

L——观察点坐标矩阵

为了充分考虑观测矩阵L和系数矩阵A的随机误差，使误差模型更合理，设EL为L的随机误差，EA为A的随机误差，由式(2)可得

L-EL=(A-EA)X

(5)

整体最小二乘的实质即为求式(6)的最佳估值。

(6)

采用整体最小二乘算法[16-17]求解转换矩阵中的位置参数，进而可确定标定坐标系o′x′y′z′的位置，迭代算法设计如下:

(2)计算

其中

式中 vec——矩阵拉直运算符号

DA——系数矩阵A的协方差矩阵

σ0——未知方差分量

⊗——矩阵克罗内科积运算符号

(3)根据拉格朗日极值条件求得

式中P——权矩阵

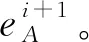
(5)根据Xi-Xi-1<ε判断迭代是否终止。ε为终止条件。

(6)计算出全部转换参数矩阵X。

1.3 基于模糊神经网络的误差参数识别与预测

针对误差模型中误差数据的处理，目前普遍采用多元线性、神经网络模型、灰色理论和支持向量机等方法进行数据拟合和预测[18-22]。采用模糊神经网络模型误差参数识别与预测模型。

1.3.1模糊神经网络结构

应用模糊逻辑理论，建立Delta-CU机构的模糊神经网络误差参数识别与预测模型。模糊神经网络结构如图3所示[23]。

第1层：输入层，节点x1,x2，…，x7表示误差模型的观测点。

第2层：隶属函数层，每个节点分别代表一个隶属函数，该隶属函数为

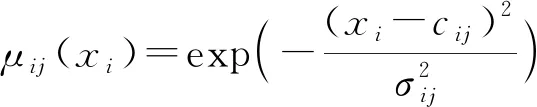
式中μij——xi的第j个隶属函数

cij——xi的第j个高斯隶属函数的中心

σij——xi的第j个高斯隶属函数的宽度

μ——隶属函数数量，表示系统总的规则数

第3层：T-范数层，每个节点分别表示一个可能的模糊规则中的IF-部分。第j个规则Rj输出为

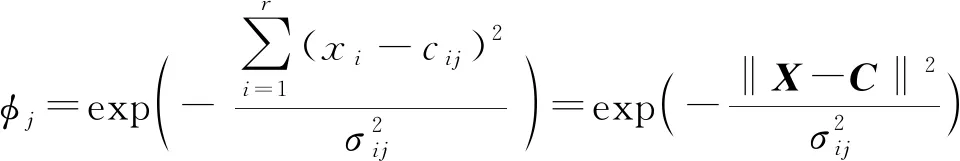
第4层：归一化层，称这些节点为N节点。第j个节点Nj的输出为

第5层：输出层，该层中每个节点表示一个输出变量。

1.3.2RBF中心和宽度的确定

对于RBF神经网络的中心，一般采用K均值聚类法来计算，但由于K均值聚类法受样本初始状态的影响较大，因此采用模糊均值聚类(FCM)方法计算中心[24-25]。

考虑一个样本集X={x1,x2,…,xn}，其中xi={xi1,xi2，…，xik}为一个k维向量。此集合依据一定的准则分成c个模糊子集，其中c是用户给定的聚类数。FCM算法是把n个样本划分成c个类别，使定义的聚类损失函数达到最小。聚类损失函数为

其中

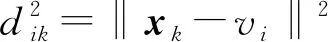
式中U——隶属度矩阵

V——聚类中心

μik——向量xk相对于第i个簇的隶属度函数

dik——xik对第i个簇的中心vi的距离

vi——第i个簇的中心

令Jm对vi和μik的偏导为0，使目标函数达到最小值的条件为

(7)

FCM算法给出一种迭代算法来近似得到目标函数的最优值，算法具体如图4所示。误差平方和e的计算公式为

(8)

若 ‖xj-vj‖2<‖xj-vl‖2(l=1,2,…,c;l≠i)

则将xj归为第i类。

模糊神经网络的宽度设定为各聚类样本到该类中心距离的均值,即

(9)

1.3.3连接权值的计算

采用最小二乘法调整连接权值。假定n个观测数据产生了u个模糊规则，N节点的输出可写成矩阵形式

对于任意的输入Xj(x1j,x2j，…，xrj)，系统输出可写成

Wφ=Y

式中W∈Ru,φ∈Ru×n。

假定理想的输出为T=(t1,t2，…，tn)∈Rn，给定φ∈R(r+1)un和T∈Rn之间的关系为

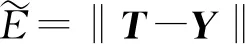
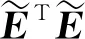
W*W=T

最优的W*为

W*=T(φTφ)-1φT

1.3.4Delta-CU操作手的误差模型与预测

考虑到操作手末端在不同的位姿和运动轨迹对误差模型的影响，采用操作手末端常用的“门”字轨迹上的7个关键点作为建模的输入观测点，如图5所示。其中，P1、P6分别为抓取点和放置点，P1P2段为上升阶段，P2P3、P4P5为圆弧过渡段，P3P4为水平移动阶段，P5P6为下降阶段，这些点的选取可同时保证模型的精度和建模的效率。

在相同的工作条件下，试验过程中采集2组数据，第Ⅰ组训练数据进行建模，第Ⅱ组试验数据用来模型测试。将第Ⅱ组得到的预测数据与实际测得数据进行对比， 如图6所示。图6中的误差为操作手在“门”字形轨迹运动过程中y方向的误差。

1.3.5Delta-CU操作手的误差补偿

误差补偿是运动学标定的核心内容，将模糊神经网络误差模型补偿到机器人系统中，以达到减小机器人系统误差的目的，采用外部直接标定补偿、用辨识结果修正系统输入的方法讲行误差补偿。设理想驱动输入矢量为Q0，M0为与理论驱动输入相对应的机器人末端位置矢量，Δm为由系统误差引起的末端位置误差矢量。机器人操作手的理论几何参数为l0，系统真实几何参数的误差为Δl，利用辨识结果修正系统输入为

Q0=f(f-1(M0-Δm,l0),l0+Δl)

(10)

式中f(·)——操作手的运动学正解模型

f-1(·)——操作手的运动学逆解模型

2 Delta-CU操作手误差补偿及实验分析

2.1 实验系统组成

实验设备主要包括：FARO Vantage型激光跟踪仪和Delta-CU并联机构系统以及计算机，如图7所示。实验所用的Delta-CU并联操作手系统，由2-RPa⊕RUU并联机构(图1)、上料机构、传送机构、真空吸盘和控制系统组成，如图8所示。RPa⊕RUU并联机构的主动臂与从动臂的长度分别为190、390 mm；主动臂转轴中心位置矢量模长名义尺寸为149 mm；制造装配时已保证了末端动平台姿态误差较小。

2.2 实验测量原理

采用直接标定法，使用外部的FARO Vantage型激光跟踪仪，直接对机器人末端位姿进行测量，获取机构执行末端的运动轨迹各点的坐标值。标定前首先用水平仪将操作手3个主动臂置水平，并将该位置定为操作手初始零点。

首先，参考机构动平台的尺寸及运动的工作空间，设计靶球工装夹具，将靶球固定在动平台上跟随动平台移动；其次，利用激光跟踪仪随机测量靶球所到达的任意5个位置点坐标，按照式(3)确定操作手的标定坐标系；最后，规划机构动平台的运行轨迹，利用跟踪仪连续记录靶球每个位置的坐标值，系统会自动计算动平台中心的坐标值；根据误差模型和补偿算法进行操作手的误差补偿。

2.3 实验结果与分析

图5为并联机器人末端操作手演示的门字形轨迹，完成一个工件的整个抓放过程中，在抓取和放置时的精度要求最高(图9)，中间过程只需要保证速度要求，因此，对抓取点P1进行位置精度分析。

为了计算操作手“门”字轨迹中抓取点P1的重复定位误差和绝对位置误差，设初始抓取点的位置为(97.127 mm, -27.358 9 mm，-379.808 9 mm)，任选15组轨迹抓取点P1的测量坐标值，如表1所示。由表1可知，抓取点P1的绝对位置精度为1.187 mm，重复定位精度为0.037 mm。根据式(10)进行误差补偿，以降低位置偏差，通过误差补偿，重复第1次实验测量过程，得到轨迹曲线，如图10所示。

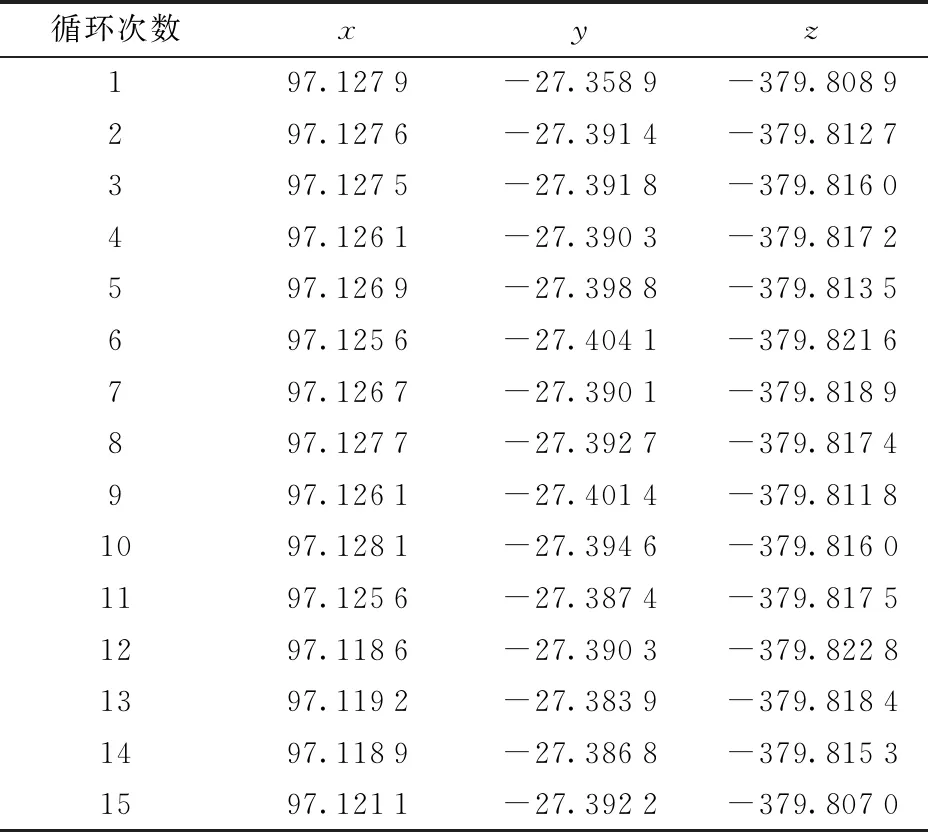
表1 抓取点P1的测量坐标Tab.1 Measurement coordinates of P1 mm

在补偿后的“门”字形轨迹中，任取一测量点进行重复定位精度和绝对位置精度的测量和标定。以抓取点P1点为例，绝对位置精度从1.187 mm提升为0.4 mm, 重复定位精度从0.037 mm提升为0.018 mm。精度提高较大，补偿效果较为明显。

针对椭圆形轨迹，进行运动学误差补偿和标定，同样可以达到较好的误差补偿效果，如图11所示。

3 结论

(1)基于模糊神经网络提出一种误差参数识别和补偿方法。在直接标定过程中，采用整体最小二乘法求解标定过程中的坐标转换参数。相对于其他方法，采用神经网络模型对误差数据进行拟合与预测具有精度高、鲁棒性好、对原始数据要求低等优点。

(2)基于激光跟踪仪，搭建了Delta-CU并联机构的误差测量平台，测算出3个平移量的误差模型，拟合得到误差变化曲线对机器人定位补偿。使用激光跟踪仪验证了补偿前后的精度，结果表明，补偿后其绝对位置精度由1.187 mm提高到0.4 mm，重复位置精度由0.037 mm提高到0.018 mm，精度提高较大，补偿效果较为明显。