基于支持向量机回归的营养液调控模型研究

崔永杰 王明辉 张鑫宇 宁普才 崔功佩,3 王 琦

(1.西北农林科技大学机械与电子工程学院， 陕西杨凌 712100； 2.农业农村部农业物联网重点实验室， 陕西杨凌 712100；3.陕西省农业信息感知与智能服务重点实验室， 陕西杨凌 712100； 4.陕西旭田光电农业科技有限公司， 陕西杨凌 712100)

0 引言

营养液为设施栽培作物提供所需的营养物质，对作物生长发育和物质积累至关重要[1]，营养液浓度不足或过高都会对作物生长产生有害影响[2-6]。同时，温度变化易使营养液检测指标值发生改变[7-9]。因此，研究适宜温室设施栽培的营养液各化合物含量与检测指标值之间的关系、构建营养液调控模型，已成为设施栽培中营养液环境高效调控亟待解决的问题。

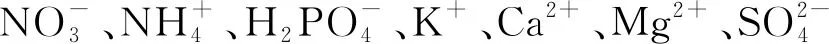
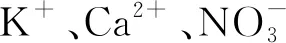
针对上述问题，在考虑营养液检测指标值、各化合物含量与调控效益的前提下，本文基于Knop配方[21]进行研究。首先，构建基于SVR的营养液检测指标值预测模型；然后，计算营养液检测指标值与5种化合物含量响应曲线的离散斜率，并利用人工鱼群算法获取斜率最大突变点；最后，以该突变点对应的5种化合物含量作为最优调控目标值，基于SVR构建营养液调控模型，以期为设施栽培中营养液的精准调控提供依据。

1 材料与方法

1.1 试验材料

试验于2020年5—6月在西北农林科技大学南校区科研温室(北纬34°14′、东经107°59′，暖温带半干旱半湿润大陆季风气候)进行。 本文对基于Knop营养液配方使用的化合物A: Ca(NO3)2·4H2O(纯度99%)、化合物B: KNO3(纯度98%)、化合物C: KH2PO4(纯度99%)、化合物D: MgSO4·7H2O(纯度98%)、化合物E: EDTA-NaFe(纯度99%)展开研究。

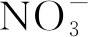
在对营养液调控效果进行试验验证的过程中，本研究使用自行研制的营养液自动调控系统进行调控试验，如图2所示。

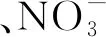
1.2 试验方法

1.2.1数据集获取

1.2.2多因素交互的营养液检测指标值预测模型

(1)将数据集进行归一化操作，以避免大数据淹没小数据现象的发生，同时便于神经网络预测与斜率计算。

(2)确定SVR算法关键参数。由于径向基核函数计算的复杂度不随参数变化而变化，故选取其作为核函数；惩罚因子c和影响因子g为主要影响参数。经网格验证方法进行多次经验计算获取最佳参数值，5种检测指标值对应关键参数，c分别为8、10、128、128、128，g分别为0.03、0.04、0.05、0.05、0.05。

(3)训练及构建模型。针对520组训练集，采用径向基核函数，通过低维空间的非线性不可分问题映射到高维空间，并在高维空间产生用于最优分类的超平面，进行线性回归决策分析。

1.2.3响应曲线斜率最大突变点获取

1.2.3.1响应曲线离散斜率计算

斜率作为常用的曲线评价指标被用于曲线特征位点的获取[25]，在营养液检测指标值响应曲线中，斜率最大突变点代表化合物含量与检测指标值相关性最大的特征位点，是构建营养液调控模型的关键。且离散斜率法计算局部区域斜率不受整条曲线的全局影响[26]，因此使用离散斜率法进行本文曲线斜率获取。离散斜率计算包含两方面内容：

c(x)=f′(x)

(1)

kpi=c(xi)

(2)

式中c(x)——拟合曲线斜率

f′(x)——拟合曲线方程一阶导数

kpi——pi点斜率

xi——pi点横坐标值

按照以上步骤对响应曲线各点求斜率，kpi为正表示曲线在当前点呈上升趋势，反之表示曲线在当前点呈下降趋势。为避免试验数据微小波动对结果产生影响，而无法准确获取斜率最大突变点，因此本研究将计算所得离散斜率统一取正值。

1.2.3.2基于人工鱼群算法的斜率最大突变点获取

本文在建立营养液检测指标值预测模型的基础上，使用基于动态调整视野和步长的人工鱼群算法[27]，完成特定温度下营养液检测指标值斜率最大突变点的寻优。动态调整公式为

v=avi-1+vmin

(3)

st=ast,i-1+stmin

(4)

式中v——本次搜索人工鱼的视野

st——本次搜索人工鱼移动的步长

vi-1——前次搜索人工鱼的视野

st,i-1——前次搜索人工鱼移动的步长

a——调节系数

vmin——视野范围最小变化量

stmin——步长最小变化量

由式(3)、(4)可得，在初值确定的条件下，视野和步长由调节系数a决定，且与a呈线性关系。因此，a变化趋势应与视野和步长保持一致，本文采用增加权值的方法构建调节系数，即

a=(1-t/Tmax)s

(5)

式中t——当前迭代次数

Tmax——最大迭代次数

s——变化速率，取[0,10]内的整数

在对关键参数进行确定时，变化速率s为2，鱼群规模为100，重复次数为100，拥挤度因子为0.618，通过上述参数设置，以此完成对营养液检测指标值斜率最大突变点的寻优。

针对以上方法，完成人工鱼位置更新以及对生成新鱼群的优化过程迭代，直到完成特定温度下营养液检测指标值离散斜率最大突变点的寻优。同时记录和保存营养液检测指标值离散斜率最大突变点对应的营养液5种化合物含量，直至获取所有响应曲线斜率最大突变点对应的5种化合物含量。

1.2.4营养液调控模型构建

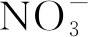
1.2.5调控效果验证

在进行调控效果验证试验时，为降低非试验因素对试验效果的影响，在同一温室的2个尺寸相同的营养液栽培槽内进行。设定温室温度16～28℃(间隔1℃)13个温度梯度试验条件，设置10组不同化合物配比且与调控目标值存在偏差的营养液进行调控试验，如表1所示。每组试验重复3次，剔除错误数据后取平均值作为试验结果。对比基于SVR的营养液调控模型组和逐步拟合响应模型组的调控效果。试验中运行基于SVR的营养液调控目标点获取模型和逐步拟合响应目标点获取模型，分别获取目标值对优化调控区和传统调控区进行调控。

2 结果与分析

2.1 营养液检测指标值预测模型验证结果

为了验证SVR算法构建预测模型的拟合效果，对比BP神经网络和ELM回归构建拟合预测模型，且与目前普遍应用于作物栽培的多元线性回归模型[18]和逐步拟合响应模型[28]等进行对比，5种模型评价对比如表2所示。

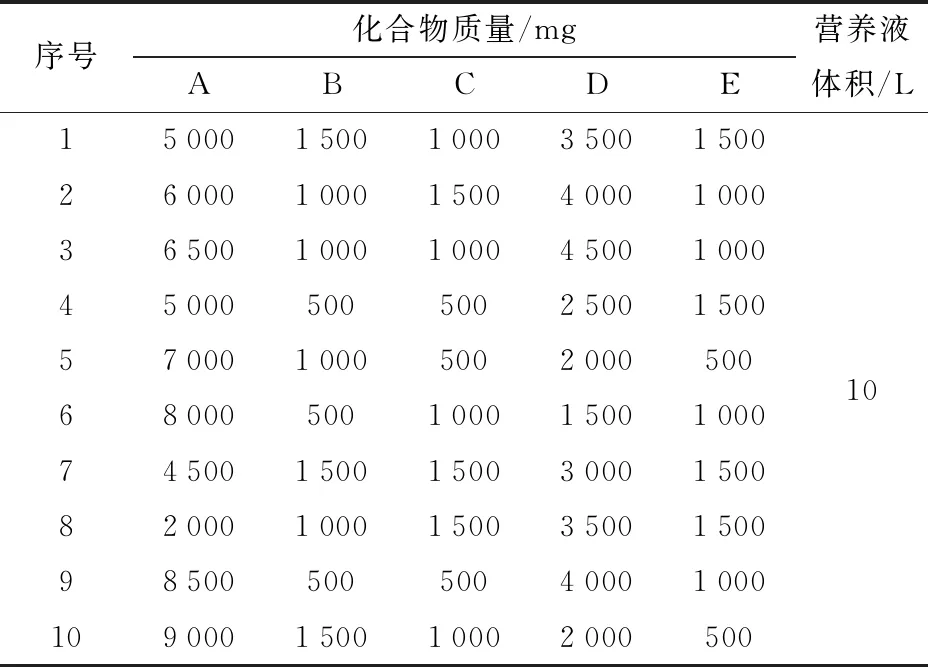
表1 10组不同化合物配比Tab.1 Ratio of 10 groups of different compounds

由表2可见，对比其他方法，SVR算法构建预测模型的决定系数最高，均方根误差最小。检测指标值预测模型的决定系数分别为0.98、0.94、0.97、0.93、0.98；均方根误差分别为1.73、3.81 μS/cm、1.79 mg/mL、0.87 mg/mL、1.53 mg/mL，证明采用SVR算法构建预测模型是可行的。

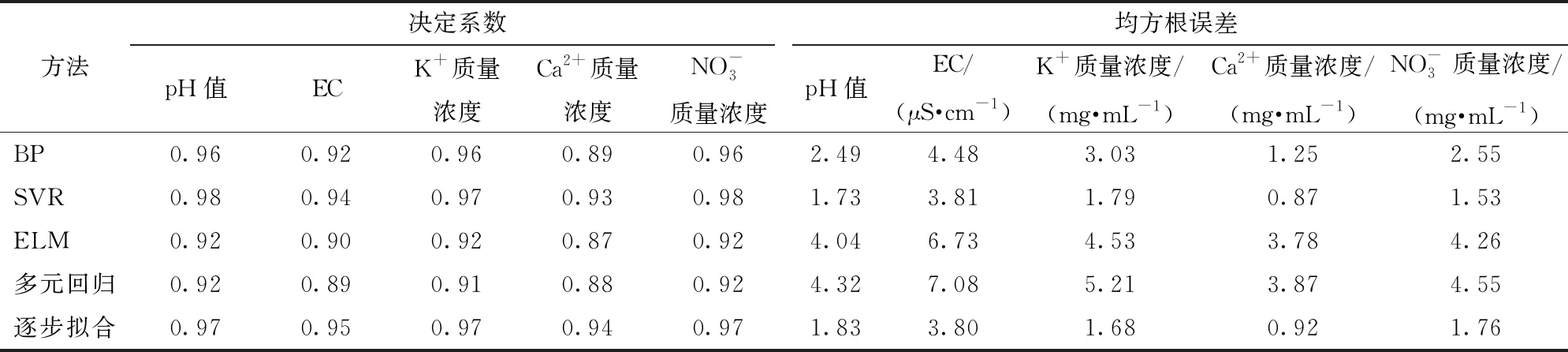
表2 5种建模方法的预测模型评价指标对比Tab.2 Comparison of prediction model indicators for five modeling methods

进一步分析可知，常用模型中逐步拟合响应模型的决定系数大于多元线性回归模型，均方根误差和平均绝对误差小于多元线性回归模型，说明逐步拟合响应模型对本文试验数据的拟合效果更好。另外，通过对逐步拟合响应模型与SVR算法预测模型进行对比分析，可以看出，逐步拟合响应模型中5种检测指标值预测模型决定系数分别为0.97、0.95、0.97、0.94、0.97；均方根误差分别为1.83、3.80 μS/cm、1.68 mg/mL、0.92 mg/mL、1.76 mg/mL，与SVR算法预测模型相应评价指标相近。这说明，SVR算法预测模型的拟合效果与逐步拟合响应模型的拟合效果相似。但逐步拟合响应模型简化了拟合过程中的复杂数据，而SVR算法预测模型则是通过将全部数据进行回归拟合所得到，其预测结果更加准确；另外，逐步拟合响应模型无法预测实测点之外的数据，而SVR算法预测模型可在保证与逐步拟合响应模型相近精度的情况下对非试验条件样本的预测，从而有效解决试验样本不足这一问题。

本研究通过异校验方式凭借验证集对营养液检测指标值预测模型的泛化能力进行验证，得到营养液5种检测指标实测值和预测值相关性如图4所示。图中直线L11、L21、L31、L41、L51分别为5种检测指标验证集数据实际值和预测值的拟合直线。其中L11斜率为0.99，截距为0.05；L21斜率为1，截距为3.63；L31斜率为0.98，截距为0.01；L41斜率为0.98，截距为0.02；L51斜率为1，截距为0.005 88，由拟合直线的斜率和截距可明显看出，营养液5种检测指标值验证数据集预测值与实测值的相关性较高。

2.2 离散曲线斜率最大突变点获取结果

2.3 营养液各化合物优化调控模型验证结果

为验证基于SVR的营养液调控模型的拟合效果，本文同时采用BP神经网络和SLM拟合2种方法构建调控模型，模型评价对比如表3所示。由表3可见，基于SVR的营养液调控模型中对应5种化合物含量的决定系数分别为0.99、0.98、0.99、0.96、0.99；均方根误差分别为4.29、7.39、5.02、2.85、3.96 mg。相较于BP神经网络和SLM拟合2种方法而言，基于SVR的营养液调控模型决定系数最高，均方根误差最低，所构建的营养液调控模型具有更高的精确度和拟合效果。

2.4 调控效果对比

2.4.1理论调控效果分析

为了进一步验证基于SVR的营养液调控模型的调控效果，本研究将基于SVR的营养液调控模型与逐步拟合响应模型获取调控目标值结果的误差进行比较。在温度试验区间16～28℃内以6℃的温度梯度为例，在给定温度和准确营养液检测指标值的条件下对5种化合物含量进行预测，对比结果如图8所示。

表3 3种建模方法的调控模型评价指标对比Tab.3 Comparison of evaluation indexes of regulation model for three modeling methods

由图8可以看出，基于SVR的营养液调控模型相比于逐步拟合响应模型获取目标值的误差更小，其中5种化合物含量的平均相对误差分别降低了37.65%、49.94%、40.53%、50.58%、42.84%。说明该方法构建的营养液调控模型可以更准确地获取调控目标值，能够为设施作物营养液优化调控提供理论基础。

2.4.2实际调控效果分析

为了验证基于SVR的营养液调控模型的实际调控效果，同时采用逐步拟合响应模型进行实际调控效果试验与基于SVR的营养液调控模型实际调控效果进行对比。试验得到不同温度、不同化合物配比下的营养液5种化合物使用量如图9所示，因数据无法全部罗列，下文仅展示温度在16～28℃范围内，以3℃为步长的化合物使用量试验结果。

由图9可发现，对比于逐步拟合响应模型，基于SVR的营养液调控模型的调控精度更高、误差更小。分析得到的130组试验数据，首先计算每种化合物实际使用量与理论使用量的相对误差，然后针对130组试验求得相对误差平均值，对比逐步拟合响应模型，基于SVR的营养液调控模型的5种化合物使用量的相对误差平均值分别降低了46.42%、52.08%、54.03%、53.59%、54.54%；计算基于SVR的营养液调控模型中5种化合物的实际使用量对比逐步拟合响应模型5种化合物的实际使用量的降低率，然后针对130组试验数据求得5种化合物使用量的平均降低率分别为1.69%、5.81%、5.85%、3.65%、7.08%。说明基于SVR的营养液调控模型进行营养液调控的方法，可以在保证检测指标值准确的情况下减少营养液5种化合物的供需量，对融合经济效益的营养液精准调控具有实际意义。本研究提出的基于SVR的营养液调控模型可在实时环境下对营养液调控目标值进行动态、高效的获取。

进一步分析可得，对比同一化合物配比、不同温度下的调控结果发现，基于SVR的营养液调控模型的5种化合物使用量基本保持稳定。说明融合温度变化的基于SVR的营养液调控模型可以在不同温度条件下有效完成营养液调控，为园艺学中作物栽培的实际生产应用提供技术依据。

3 结论

(1)提出一种基于SVR的营养液调控模型，解决了设施栽培中营养液动态调配精度低的问题，可为设施栽培中营养液精准调控提供参考。

(2)构建的营养液检测指标预测模型的决定系数分别为0.98、0.94、0.97、0.93、0.98，均方根误差分别为1.73、3.81 μS/cm、1.79 mg/L、0.87 mg/L、1.53 mg/L。与BP神经网络和ELM网络构建的预测模型相比，能以更高精度拟合多因子输入下的营养液检测指标值。

(3)基于SVR构建的营养液调控模型对应5种化合物含量的决定系数分别为0.99、0.98、0.99、0.96、0.99，均方根误差分别为4.29、7.39、5.02、2.85、3.96 mg，拟合效果良好。比BP神经网络和ELM网络构建的营养液调控模型能更准确地调控目标值。

(4)对比逐步拟合响应模型获取调控目标值的结果发现，基于SVR的营养液调控模型5种化合物含量的平均相对误差分别降低了37.65%、49.94%、40.53%、50.58%、42.84%；在调控效果验证试验中，对比逐步拟合响应模型发现，基于SVR的营养液调控模型5种化合物使用量的相对误差平均值分别降低了46.42%、52.08%、54.03%、53.59%、54.54%，调控过程中5种化合物使用量的平均降低率分别为1.69%、5.81%、5.85%、3.65%、7.08%。在不同温度下进行调控时，基于SVR的营养液调控模型5种化合物使用量基本保持稳定，能够基于实时环境对营养液进行动态、精准的调控。