基于LMBA策略的鄂尔多斯市生态空间网络优化

侯宏冰 郭红琼 于 强 毛雪晴 龙芊芊 岳德鹏

(1.北京林业大学精准林业北京市重点实验室， 北京 100083;2.中国地质科学院水文地质环境地质研究所， 石家庄 050061)

0 引言

景观格局反映地物空间结构特征，不同地物的形状、排列组合方式会形成不同的景观格局，景观格局的形成和演变是人类活动和自然因素共同作用的结果。随着人类社会的不断发展，由于土地长期不合理的利用，导致原有天然生态环境遭到破环，景观变得脆弱。生态环境的变化表现在景观格局变化上，景观格局影响着生物群落分布和迁移运动，而生物群落分布和迁移变化又影响着景观格局的变化，从而影响生态环境。因此，景观格局是研究生态环境和生物相互关系的纽带。

国内外对景观格局的研究主要集中在景观分类、景观变化驱动机制及景观格局应用等方面。目前的研究方法多集中于概念模型和数学模型。为了维持区域生态安全，许多研究者针对原有地表类型的格局分布，对其规划调整进行了研究，以此维持并提升区域生态系统多样性和稳定性，改善和修复环境[1-2]。生态空间网络将景观格局看作一个整体，从复杂网络理论角度分析生态空间网络、用拓扑结构分析生态空间网络的结构，可以从整体上提升景观格局的功能，在保证自然生态健康发展的同时，实现社会、经济的最优发展。本文基于景观生态学和复杂网络理论，利用生态空间网络分析景观格局，在网络拓扑结构分析的基础上提出优化策略，对网络结构进行优化，以期为区域景观格局优化提供参考。

1 材料与方法

1.1 研究区概况

研究区鄂尔多斯介于北纬37°35′24″～40°51′40″，东经106°42′40″～111°27′20″(图1)。东、北、西部均有黄河分布，南部是黄土高原地区。鄂尔多斯地区位于北温带，区域较为干旱。降水量较为稀少，雨季为7—9月，气温温差大，多年平均气温6.2℃，区域蒸发量严重大于降水量，5—7月蒸发量最高。区域盛行西风和西北风，风速最高可以到22 m/s。鄂尔多斯市土地利用类型面积最大是草地和裸地，裸地中库布齐沙漠大部分位于西北部杭锦旗中，毛乌素沙地大部分位于东南部的乌审旗，农田、水体、林地和建设用地面积较小且大多位于东北地区。

1.2 数据来源与处理

本研究使用的2018年土地利用数据、归一化植被指数(Normalized difference vegetation index，NDVI)数据、气象数据来源于资源环境云平台(http:∥www.resdc.cn/)，数字高程模型(Digital elevation model，DEM)数据来自地理空间数据云(http:∥www.gscloud.cn/)，分辨率为30 m，并从中提取了坡度数据。改进的归一化差异水体指数(Modified normalized difference water index，MNDWI)数据利用Landsat OLI影像的波段3和波段6提取得到，道路和河流数据来自OpenStreetMap(http:∥www.openstreetmap.org/)。

1.3 方法

1.3.1生态空间网络提取

生态空间网络基本单元包括生态源地、生态廊道和生态节点。生态源地是区域景观生态空间网络的重要基本单元。本文根据鄂尔多斯主要生态类型为草地且荒漠化较为严重的特点，选择林地、草地、水体3种景观类型斑块[3]。首先计算各斑块的面积、NDVI、MNDWI以及斑块形状指数；再利用熵值法确定这4个指标的权重，文中4个指标权重分别为0.5、0.2、0.2、0.1；最后确定各斑块的综合重要性程度，筛选出重要性排序在前60%的斑块作为生态源地。

生态廊道是景观生态流从某一生态源地经阻力面到另一生态源地的众多路径中最优的一条[4]。本文将生态节点分为源地型和薄弱型两类，前者指生态源地空间分布质心，后者位于生态廊道最薄弱处。根据研究区生态环境特征，选取高程、坡度、NDVI、MNDWI、土地利用类型、居民点密度、路网密度、水网密度8个因子评价研究区各空间位置的阻力[5]。利用最小累积耗费阻力模型(Minimum cumulative resistance,MCR)构建生态累积阻力面。最后利用成本路径模型在生态累积阻力面的基础上提取出生态廊道，该模型的原理是根据累积阻力面为每个像元分配成本，不断迭代识别从源地出发的成本最小的邻近像元，最终形成最小成本路径。提取生态累积阻力面的山脊线，山脊线与生态廊道的交点就是薄弱型生态节点[6]。

1.3.2拓扑结构分析

网络拓扑结构是影响复杂网络中生态流传输的一个重要因素[7]。在干旱半干旱地区，生态空间网络是生态环境稳定最基本的保障，所以干旱半干旱区的生态廊道都极为重要，因此本文将鄂尔多斯生态空间网络假设为一个无权无向的复杂网络[8]。选用无向无权网络常用指标分析该网络的拓扑结构特征。

复杂网络中节点的度指与该节点相连的其他节点数量。节点的度分布通常符合某种统计规律，完全随机网络的度分布符合Poisson分布[9]，但实际网络通常并非随机，度分布往往呈现出一定的幂律分布特征。节点间的距离是它们之间最短路径上边的条数[10]。网络直径和平均路径长度即为网络中所有最短路径中的最大值和平均值[11]。复杂网络中3个节点同时互相连通的特性被称为聚类特性[12]。网络平均聚类系越大表明节点间的联系越紧密[13]。实际生态空间网络中节点的度之间的相关性被称为度-度相关性，是衡量网络中的节点在与其他节点连接时的某种偏好[14]。节点介数定义为复杂网络中所有通过该节点的最短路径与网络中所有无论是否通过该节点的最短路径的比例[15]。复杂网络k核指在去除网络中所有度小于k的节点之后剩余的网络子集[16]。网络核数指网络中最大的节点核数[17]。网络平均度、平均路径长度、度-度相关性、核数计算式为

(1)

(2)

(3)

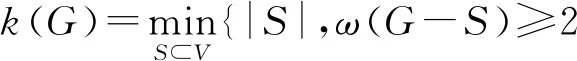
(4)

生态节点i的聚类系数、介数计算式为

(5)

(6)

式中 〈k〉——网络平均度

N——网络中节点总数

ki——网络中编号为i节点的度

L——网络平均路径长度

dij——节点i与j之间的最短路径长度

r——网络度-度相关性

kj——边eij一端节点j的度

M——网络中所有边的数量

E——网络中所有边组成的集合

V——网络G的节点集合

S——V的真子集

ω(G-S)——从图G中删除点集S所有节点及与之关联的所有边后的子图连通分支数

Ci——生态节点i的聚类系数

Ei——节点i与m个邻居节点间的实际生态廊道数

Bi——节点介数

njl——节点j和l之间的最短路径条数

njl(i)——节点j和l之间最短路径经过节点i的条数

1.3.3鲁棒性分析

生态空间网络的鲁棒性可以认为是当网络的结构发生变化时，该网络维持其正常结构与功能的能力[18-20]。对网络的攻击方式通常分为随机攻击和恶意攻击两种，随机攻击是在网络中随机选择节点或边进行破坏，而恶意攻击是优先选择度高的节点或介数较高的边进行攻击。网络维持其本身连通功能的能力被称为连接鲁棒性，网络结构在遭到破坏后的恢复能力被称为恢复鲁棒性。鲁棒性计算公式为

(7)

(8)

(9)

式中R——网络连接鲁棒性

C——最大连通子图中节点的数量

Nr——被移除的节点数目

DR——节点恢复鲁棒性

Nd——网络在移除Nr个节点后恢复的节点数目

ER——边恢复鲁棒性

Me——网络在移除Mr条边后恢复的边数量

1.3.4生态空间网络优化

通过对网络结构进行微小的调整，使其更为稳定，可以发挥出本身最大的生态功能。根据研究区生态脆弱的情况，选择增边策略优化鄂尔多斯生态空间网络，并基于节点介数提出了节点最低和最大介数增加(Low and maximum betweenness addition，LMBA)优化策略，同时采用随机增加(Random addition，RA)、度低者优先(Low degree first，LDF)、最大介数节点增加捷径(Shortcut for maximum betweenness，SMB)策略做对比，分析优化后网络的拓扑结构及鲁棒性。所有优化策略设置相同的增边数量Na。

2 结果与分析

2.1 生态空间网络提取

生态累积阻力面与生态空间网络如图2所示。由图2a可知，研究区生态累积阻力最大值为1 181 545，最小值为0。阻力最大值主要出现在北部库布齐沙漠以及杭锦旗东部、乌审旗北部的沙地中，这些区域生态环境状况较为恶劣且远离生态源地，耗费阻力有较明显的累积作用。最终确定出199块源地斑块、源地间直接相连的402条生态廊道、63个薄弱型生态节点(图2b)。整个鄂尔多斯的生态空间网络分成东西两部分。城区多集中在东部生态空间网络，交通便利且植被覆盖度较高，源地斑块面积较小，斑块间距离较远，生态廊道较长但较为丰富。西部生态空间网络中源地面积较大，草地源地斑块间位置紧邻，北部水体斑块之间生态廊道顺势而连。两部分生态空间网络间的连接斑块较少。此外，西北部和东南部生态阻力最高值区域出现生态廊道空白。

2.2 生态空间网络拓扑结构及鲁棒性分析

鄂尔多斯生态空间网络的拓扑结构和鲁棒性如图3所示。网络平均度、直径、平均路径长度、平均聚类系数分别为2.39、38、13.40、0.066，网络直径和平均路径均较长，聚类系数较低，说明该网络不具备小世界特性。网络度分布的幂律分布特征比Poisson分布更明显。网络中没有度为0的孤立节点，大多数节点的度都较低，90%的节点度为1、2、3，最大度也仅为32，说明该网络由少量大型生态节点连接其他小型节点。网络中节点聚类系数总体偏低且差异性较大，86%的生态节点的聚类系数为0，8个生态节点聚类系数为1，表明该网络中的生态廊道在某些区域分布密集，而大部分地区的网络连接很稀疏。网络的度-度相关性r为-0.086，网络呈现出异配性。聚-度双对数相关性显示，随着节点度对数的增加，聚类系数对数先增加后下降，但下降趋势非线性，说明该网络是非层次网络[21]。网络中有178个生态节点的介数为0，仅1个节点介数达到418，位于网络西部；同时，网络核数仅为3，仅4个节点核数为3且都位于西部生态网中，说明网络结构不均匀，重要节点重心西偏。网络中92%的节点连通度低于10，连通度最大为25。拓扑结构分析表明研究区网络连通情况极差且网络重心西偏，不利于网络间的物质、能量与信息的交换，对恶意攻击的鲁棒性很弱，网络急需优化。

利用恶意攻击和随机攻击两种模式攻击网络，整体来看，随着攻击规模的增加，网络结构在恶意攻击下的鲁棒性明显低于随机攻击。网络的初始连接鲁棒性在两种攻击模式下都仅为0.90。恶意攻击下，“涌现”现象出现在攻击节点数为2时，连接鲁棒性骤降至0.58，当攻击节点数为7时，降为0.27，网络连通性极差。随机攻击下，“涌现”现象出现在攻击节点数为41～47之间，从0.65降至0.40左右，在攻击节点数为67时，“涌现”现象再次出现，降低到0.20左右，网络结构的连接功能几乎完全丧失。网络的节点恢复鲁棒性的下降趋势在两种攻击模式下都类似一条“凸”曲线，初始节点恢复鲁棒性都为1，在攻击节点数为36时，网络中遭到破坏的节点都可以完全恢复。在攻击节点数为200时，随机攻击下的节点恢复鲁棒性还有0.58，恶意攻击下也还有0.42，说明网络节点恢复功能较强。边恢复鲁棒性在两种攻击下的下降趋势也很相似，类似一条直线，恶意和随机攻击分别在攻击边数为3和11时，受到攻击的边还能完全恢复，在攻击边数为200时，随机攻击下为0.42，恶意攻击下为0.26。总体来看，网络边恢复鲁棒性不如节点恢复鲁棒性，但明显强于连接鲁棒性。说明该网络的网络结构在遭到破坏时，网络结构进行自我恢复的能力比较强，但维持自身的连通能力非常弱。

2.3 生态空间网络优化及对比

2.3.1生态空间网络优化

利用提出的LMBA策略以及RA、LDF、SMB策略同时对鄂尔多斯生态空间网络进行优化，增边数量均设置为现有生态廊道数的30%，即94条。优化后的生态空间网络如图4所示。由图4可知，优化后的网络廊道分布都比较均匀，因为RA策略是在节点间随机增边；LDF策略侧重在网络边缘度低的节点间增边，网络东西分布较为均匀；SMB策略在重要节点周围增加廊道，使重要节点向东部延伸，网络整体分布也比较均匀；LMBA策略除了使重要节点向东延伸外，也改善了低介数节点的连通性，提高了网络的整体连通性。

2.3.2优化后生态空间网络拓扑结构及鲁棒性对比4种策略在网络中都增加了相同的边数，但增边位置不同，所以优化后网络的平均度均为3.11，网络直径、平均路径长度、度分布以及聚类系数却不相同(表1)。优化后网络直径和平均路径长度明显降低，度明显增加。综合来看，RA策略优化后网络直径、平均路径长度和聚类系数都是最低的，网络中节点间的连通性最强，节点不聚集；SMB策略优化后网络的直径、平均路径长度和聚类系数都最高，节点聚集程度较高，但网络连通性不太高；LDF策略和LMBA策略相似，但LMBA策略直径、平均路径长度更短，聚类系数也稍低，和优化前相当。

4种策略优化后网络的拓扑结构如图5所示。由图5可知，优化后网络中节点的度明显提升，RA策略度最高为33；LDF策略和LMBA策略都不存在度为1的节点，度最高值为32；SMB策略节点度最高为42。网络度分布都呈轻微的Poisson分布特征，网络更均匀。4种网络聚类系数为0的节点占比分别为82%、73%、77%、78%，相比优化前明显降低。SMB策略中聚类系数为1的节点明显增加，其余策略均减少，且LMBA策略的最大值仅为0.5。4种网络的度-度相关性r分别为-0.070、-0.037、0.114、-0.010，异配性均降低，SMB策略甚至出现了同配性。网络的聚-度双对数相关性显示LDF和LMBA策略呈一定的线性关系，RA策略的线性关系虽不明显，但也略优于优化前，SMB策略没呈现出线性特征。4种网络中介数最大值分别是1 087、1 313、634、796，都明显提高。优化后网络的核数和连通度明显增强，RA、LDF、LMBA策略网络核数均为3，所有节点核数都为3；SMB策略网络核数为8，核数为8的节点共10个且在网络中均匀分布，但核数为2的节点有227个，说明SMB策略仅优化了部分节点的核数。4种网络中节点连通度在20以下的节点占比分别为85%、81%、88%、84%，最高值分别为51、45、39、49，明显上升。这说明优化后网络中的重要节点增多，网络整体的效率与鲁棒性有明显的提升，网络更有利于节点间物质、能量与信息的交换，RA、LDF、LMBA策略使网络连通性极大增强，大部分节点核数增加，而SMB策略的连通性增强效果不太显著，且部分节点核数大大增强，但网络重心向中间靠拢，网络结构更均匀。

表1 优化后网络的基本静态统计特征对比Tab.1 Comparison of basic static statistical characteristics of optimized network

4种策略优化后网络的初始连接鲁棒性均为1，说明网络连通性大大增强，网络结构更加稳定。除LDF策略的连接鲁棒性在攻击后期恶意攻击明显优于随机攻击外，其他策略都是随机攻击优于恶意攻击。随机攻击下，RA策略在攻击节点数为116～170时属于快速下降期，从0.92下降至0.20左右；LDF策略从攻击节点数为38时开始急剧下降，到攻击节点数为94时，下降到0.17；SMB策略全程下降速度都比较平稳；LMBA策略在攻击前期和后期下降趋势近似线性，攻击节点数为137时出现“涌现”现象，从0.488骤降到0.266。恶意攻击下，RA策略在攻击节点数为33～60之间从0.89下降到0.25；LDF策略在攻击初期下降，攻击节点数为66～160时反而增强，随后下降，攻击节点数为193时低于0.20；SMB策略在攻击节点数为2～26时从0.96直线下降至0.27，之后缓慢下降，攻击节点数为67时低于0.20；LMBA策略在攻击节点数为66～67时从0.67降到0.46，攻击节点数为119时降低到0.20以下。整体来看，随机攻击下RA策略的效果最好，LDF策略效果最差，LMBA策略在出现“涌现”现象前优于SMB策略，整体效果相对更好。而恶意攻击下，LMBA策略整体效果最优也最稳定，RA策略在前期优于LDF，但LDF策略后期回升，甚至超过其他3种策略，SMB策略整体效果最差。

4种策略优化后网络的节点和边恢复鲁棒性都是随机攻击优于恶意攻击(图6)，且初始恢复鲁棒性以及攻击节点或边数达到200时的鲁棒性都基本相同。随机攻击下，4种策略的节点恢复鲁棒性开始出现下降的攻击节点数分别为91、66、55、109，边恢复鲁棒性开始下降的攻击边数分别为42、36、5、17，之后的下降趋势都大致相似，说明随机攻击下除SMB策略在攻击前期的节点恢复鲁棒性和初期的边恢复鲁棒性以及LDF策略后期的边恢复鲁棒性甚至有所降低外，其余策略的恢复鲁棒性相对于优化前都有所提升，LMBA策略的节点恢复鲁棒性优化效果最好。恶意攻击下，4种策略的节点恢复鲁棒性开始出现下降的攻击节点数分别为71、38、26、24，边恢复鲁棒性开始下降的攻击边数分别为5、8、3、5，LDF策略的节点恢复鲁棒性和SMB策略的边恢复鲁棒性下降曲线呈轻微的“凹”曲线特征，其余策略都和优化前大致相当。说明恶意攻击下，节点恢复鲁棒性的优化效果RA策略最好，其次为LMBA策略，LDF策略最差。边恢复鲁棒性的优化效果为SMB策略最差，其他3种策略中，RA策略、LMBA策略、LDF策略分别是在攻击前期、攻击中后期、攻击后期表现最优。

从拓扑结构和鲁棒性分析结果来看，本文提出的LMBA策略优化后的鄂尔多斯生态空间网络直径、节点的介数、核数、连通度都有很大提升，且在4种策略对比中都较优，连接鲁棒性在两种攻击模式下以及节点恢复鲁棒性在随机攻击模式下表现最优，恶意攻击下以及边恢复鲁棒性在两种攻击模式下表现较优且稳定，说明该策略综合表现最优，网络连通性最强，结构均匀，且在遭到攻击过程中，维持自身连通情况和恢复能力较优且稳定。

3 结论

(1)鄂尔多斯生态空间网络有262个生态节点、402条边，网络直径为38，节点最大介数为418，最大连通度为25。网络连通度低，重要节点少且均位于网络西部，网络极不均匀，说明研究区网络连通情况极差，且网络重心偏西，不利于网络间物质、能量与信息的交换。利用恶意攻击和随机攻击两种模式攻击网络，发现网络连接鲁棒性在遭到攻击时下降极快，恢复鲁棒下降较为缓慢，说明在遭到破坏时，该网络结构进行自我恢复的能力比较强，但维持自身连通的能力非常弱。

(2)提出LMBA策略优化网络，同时与RA策略、LDF策略、SMB策略进行了对比，4种策略的增边数量均为94条。结果表明，LMBA策略优化后网络直径为16，节点最大介数为796，最大连通度为49，说明网络重要节点增多，网络整体效率明显提升。RA策略、LDF策略也使网络节点连通度极大增强，大部分节点核数增加；SMB策略的节点连通度增强效果不显著，重要节点增多且向东移，网络结构更均匀。遭到攻击后，网络的连接鲁棒性大大增强，恢复鲁棒性也有所提升。与其他策略相比，LMBA策略的连接鲁棒性在两种攻击模式下、节点恢复鲁棒性在随机攻击模式下表现最优，节点恢复鲁棒性在恶意攻击下、边恢复鲁棒性在两种攻击模式下表现较优且稳定，说明该策略网络连通性强、结构均匀，综合表现最优。在遭受攻击过程中，LMBA策略维持自身连通情况的能力较优且稳定。