NORX算法中非线性组件的移位参数选取准则研究*

沈 璇,何 俊

(国防科技大学 信息通信学院，湖北 武汉 430010)

凯撒竞赛(Competition for Authenticated Encryption:Security,Applicability,and Robustness，CAESAR)[1]是由著名密码学家Bernstein发起的一项寻求安全高效认证加密算法的全球性活动。该竞赛得到了美国国家标准技术研究所 (National Institute of Standard and Technology,NIST)的大力支持。CAESAR于2014年开始，第一轮共收到了来自全球各个密码团队提交的57个候选算法，其中有29个候选算法进入了第二轮，15个候选算法进入了第三轮，并最终在2018年针对不同的应用场景评选出了7个获胜算法。NORX算法[2]是进入该竞赛第三轮的候选算法。

自NORX算法发布以来，许多密码学者从不同角度对其安全性进行了研究。Aumasson等[3]在Latincrypt 2014上首先分析了其内部置换函数的差分特性。进一步，Das等[4]给出了内部置换函数的高阶差分特性。接着，Bagheri等[5]在FSE 2016上给出了NORX置换函数缩减到2轮的密钥恢复攻击。后来，Biryukov等[6]在2017年给出了NOXR置换函数的一些非随机特性。最近，Chaigneau等[7]利用NORX算法置换函数的对称性质构造了唯密文伪造攻击和密钥恢复攻击。

在密码算法中，非线性组件的选择对于密码算法的安全强度具有至关重要的作用[8]。为了提高硬件的实现效率，NORX算法的唯一非线性组件采用异或、与和移位操作的组合来代替模加操作。在这种组合中,移位参数的选取具有十分重要的作用。为了研究的方便，称NORX算法中非线性组件移位参数任取的函数为可变移位函数。在NORX算法的设计文档中，设计者将移位参数选取为1，但是并没有从算法安全性的角度进行说明。因此，本文通过研究可变移位函数的密码学性质来探讨NORX算法中非线性组件移位参数的选取准则。

模加操作是密码算法常用的非线性组件，它具有良好的密码学性质。因此，本文将研究可变移位函数对模加函数的非线性逼近性质。当可变移位函数取不同移位参数时，若其逼近概率越高，则说明它越接近模加操作，其非线性逼近性质也越好。此外，循环分析方法[9-10]是近些年来针对模加循环异式(Addition,Rotation,XDR,ARX)型密码算法十分有效的一种分析方法，它对包括BLAKE2[11]、Keccak[12]、Skein[13]等在内的许多Hash函数具有十分显著的攻击效果。不仅如此，由循环分析方法发展而来的循环异或分析方法[14-15]也是最近针对ARX型密码算法进行安全性分析的热点。循环分析方法的关键是研究循环对通过算法非线性组件的循环概率。因此，本文还将研究可变移位函数的循环概率表达式。若其最大循环概率越低，则它抵抗循环攻击的能力越强。

在非线性逼近性质方面，本文证明了随着移位参数k的变化，可变移位函数的逼近概率是一个关于移位参数k的三值函数。其中：当k=0时，逼近概率最小；当k=1时，逼近概率最大；当k≥2时，逼近概率是与移位参数k无关的常值。在循环性质方面，本文从理论上给出了不同移位参数下可变移位函数循环概率的显性表达式，并且证明了对于任意非零移位参数而言，可变移位函数均能够取得相同的最大循环概率。这两类密码学性质的研究在一定程度上揭示了移位参数的选取准则，对设计类似非线性组件的算法具有较强的指导意义。

1 预备知识

1.1 符号标记

表1给出了后文涉及的符号标记。

表1 文中涉及的符号含义Tab.1 Some notations used in this paper

1.2 NORX算法简介

NORX算法是由密码学者Aumasson等在2014年提交给CAESAR竞赛的一个轻量级认证加密算法，该算法的整体框架采用海绵结构。NORX算法的内部置换函数是基于ARX设计的，它的算法设计思路来源于密码算法ChaCha[16]和BLAKE2[17]。为了实现轻量化，NORX算法并没有采用密码学性能良好的模加操作，而是采用异或、与和移位操作的组合来代替，即用X⊕Y⊕XY≪1代替X+Y。考虑到本文的研究只涉及NORX算法中的非线性组件，有关算法其他细节的描述参见文献[2]。另外，设计者在算法文档中只给出了非线性组件X⊕Y⊕XY≪1来源于等式

X+Y=(X⊕Y)+(XY)≪1

但并未从密码安全的角度对X⊕Y⊕XY≪1中移位参数的选择进行说明。本文主要从密码学角度对NORX算法中非线性组件移位参数的选择进行探讨。为了在后文中描述方便，令可变移位函数为：

fk(X,Y)=(X⊕Y)⊕((XY)≪k)

注意到当k=1时，f1(X,Y)即是NORX算法中的非线性组件X⊕Y⊕XY≪1。

2 可变移位函数的非线性逼近性质分析

本节主要研究了可变移位函数的非线性逼近性质。在这一节中，先研究了可变移位函数与模加函数相等时的等价条件，然后利用该条件计算可变移位函数逼近模加函数的精确概率值，最后对本节进行了总结。

首先，给出如下引理。

引理令X=(xn-1，xn-2，…，x1，x0),Y=(yn-1，yn-2，…，y1，y0),这里xi,yi∈F2。并且设g(X,Y)=X+Y,fk(X,Y)=(X⊕Y)⊕((XY)≪k)，则有：

(1)

证明：因为g(X,Y)=X+Y=X⊕Y⊕C,这里C=(cn-1，…，c1，c0) 且有：

(2)

因此，fk(X,Y)=g(X,Y)⟺C=(XY)≪k。下面通过逐比特比较的方法，分k=0,k=1,k≥2三种情况进行讨论。

情形1：当k=0时,C=XY,即

(3)

则有xiyi=0,i=0,1,2,…,n-1。

情形2：当k=1时,C=(XY)≪1,即

(4)

则有xiyi(xi+1⊕yi+1)=0,i=0,1,2,…,n-3。

情形3：当2≤k≤n-1时,C=(XY)≪k,即

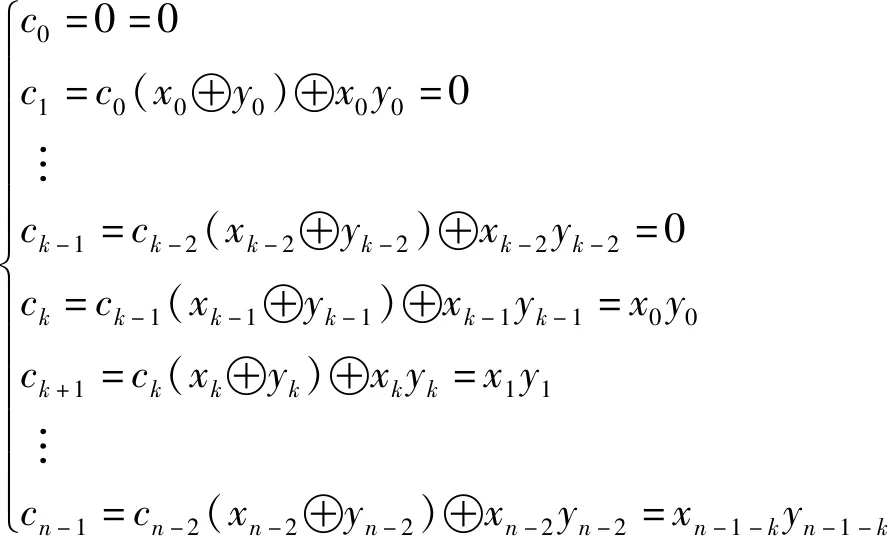
(5)

则有xiyi=0,i=0,1,2,…,n-2。因此，上述引理成立。

□

利用上述引理，可以得到如下定理。

(6)

则有

(7)

且

(8)

证明：根据引理得到如下情形。

情形1：当k=0时,X+Y=(X⊕Y)⊕XY⟺xiyi=0,i=0,1,2,…,n-1。对于任意的xiyi=0,(xi,yi)可取(0,0)、(0,1)、(1,0)这3种情况，因此

(9)

情形2：当2≤k≤n-1时,X+Y=(X⊕Y)⊕((XY)≪k)⟺xiyi=0，这里i=0,1,…,n-2。当0≤i≤n-2时，对于任意的xiyi=0,(xi,yi)可取(0,0)、(0,1)、(1,0)这三种情况。当i=n-1时，xi、yi无限制，可取所有可能的4种情况。因此

(10)

情形3：当k=1时，因为

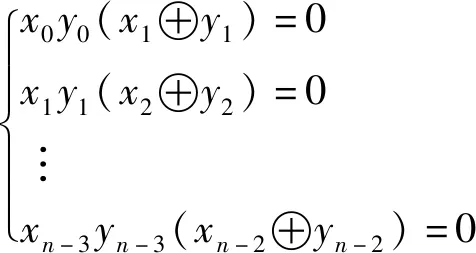
(11)

令Fn(x0,…,xn-3,xn-2,y0,…,yn-3,yn-2)=0表示上述方程组，并且令

(12)

因为0⊕0=1⊕1,0⊕1=1⊕0,所以

(13)

记方程组Fn(x0,x1,…,xn-2,y0,y1,…,yn-2)=0解的数目为Nn，则有：

(14)

注意到 (xn-1,yn-1) 可以取 (0,0)、(0,1)、(1,0)、(1,1)这4种情况，因此有

(15)

因为Fn(x0,x1,…,xn-2,y0,y1,…,yn-2)=0当且仅当

(16)

所以

(17)

化简上述方程组得：

(18)

注意当n=3时,方程组即为x0y0(x1⊕y1)=0。因此

(19)

则

(20)

令

(21)

则有A=QΛQ-1。因此

(22)

则

(23)

□

从定理1中可得，对于任意n比特长的两个数据块，能够计算出不同移位参数k下可变移位函数的逼近概率，如表2所示。

表2 可变移位函数在不同移位参数下的逼近概率Tab.2 Approximation probability of variable shift function when k takes different values

从定理1和表2可知：当k=1时，fk(X,Y)的逼近概率最大；当k=0时，fk(X,Y)的逼近概率最小。此外，当k≥2时，不管移位参数取何值，fk(X,Y)的逼近概率均相同，并且其概率大小为中间值。当移位参数fk(X,Y)给定时，数据块的规模n越大，fk(X,Y)的逼近概率越小。考虑到逼近概率越高，非线性逼近的性质越好，在NORX算法中移位参数取1达到了最佳的非线性逼近。

3 可变移位函数的循环性质分析

上一节研究了可变移位函数的非线性逼近性质，本节主要研究该函数的循环性质。首先介绍关于函数的循环对概念，然后给出一个关于可变移位函数循环概率的定理，最后对本节进行总结。

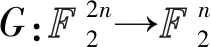
G(X,Y)≫≫r=G(X≫≫r,Y≫≫r)

(24)

下面给出一个关于可变移位函数循环概率的定理。

定理2令X、Y是n比特串,移位参数k满足0≤k≤n-1,循环参数r满足1≤r≤n-1，并且fk(X,Y)=(X⊕Y)⊕((XY)≪k)，则(X,Y)关于可变移位函数fk(X,Y)循环对的概率为：

(25)

证明：根据fk(X,Y)的具体形式知

fk(X,Y)≫≫r=

((X≫≫r)⊕(Y≫≫r))⊕((XY)≪k)≫≫r

(26)

并且

fk(X≫≫r,Y≫≫r)=

(X≫≫r)⊕(Y≫≫r)⊕((X≫≫r)(Y≫≫r)≪k)

(27)

因此

fk(X,Y)≫≫r=fk(X≫≫r,Y≫≫r)⟺

((XY)≪k)≫≫r=(X≫≫r)(Y≫≫r)≪k

(28)

令Z=XY,则

fk(X,Y)≫≫r=fk(X≫≫r,Y≫≫r)⟺
(Z≪k)≫≫r=(Z≫≫r)≪k

(29)

当k=0时,

f0(X,Y)≫≫r=f0(X≫≫r,Y≫≫r)

(30)

始终成立，即

P(f0(X,Y)≫≫r=f0(X≫≫r,Y≫≫r))=1

(31)

当1≤k≤n-1时,分r≤k和r>k两种情况进行讨论。

情形1：当r≤k,则有

(32)

根据式(29)可得zj=0，这里

j=0,1,…,r-1,n-k,n-k+1,…,n-k+(r-1)

(33)

(34)

情形2：当r>k,则有

(35)

根据式(29)可得zj=0，这里

j=r-k,r-k+1,…,r-1,n-k,…,n-1

(36)

P(fk(X,Y)≫≫r=fk(X≫≫r,Y≫≫r))

(37)

因此，上述定理成立。

□

由定理2知：当k=0时,f0(X,Y)的循环概率为1；当1≤k≤n-1时,fk(X,Y)的循环概率在循环参数r=1时均能达到最大，并且最大概率均为9/16。注意到文献[9]中引理11只是本文定理2中关于移位参数k=1时的推论。

在密码算法中，非线性组件的循环概率越低，越有利于抵抗循环攻击。因此，从循环概率值的分布情况看，移位参数取非零值时对应的可变移位函数具有更好的循环性质。进一步，不管非零移位参数取何值，可变移位函数在循环参数r=1时均能达到相同的最大循环概率。

4 结论

本文从非线性逼近和循环分析两方面研究了NORX算法中非线性函数的移位参数选取准则。研究结果表明：从抵抗密码攻击的角度看，当移位参数为0时，可变移位函数的非线性逼近和循环性质均最差；当移位参数为1时，其非线性逼近和循环性质均最好；当移位参数为其他值时，其具有相同效果的非线性逼近和循环性质。因此，NORX算法中唯一非线性组件的移位参数取1时达到了最佳的非线性逼近和循环性质。本文对NORX算法中非线性函数移位参数选取准则的探讨，不仅有助于提高NORX算法的安全性分析结果，而且还对设计类似组件函数的算法提供了理论指导。