基于自适应模型预测的智能汽车轨迹跟踪控制研究
2021-02-01路宏广聂小芮顾凯峰
路宏广 聂小芮 顾凯峰
(重庆交通大学 机电与车辆工程学院,重庆400074)
主题词:轨迹跟踪控制 自适应控制 模型预测控制 智能驾驶
缩略语
MPC Model Predictive Control
ACC Adaptive Cruise Control
NMPC Nonlinear Model Predictive Control
LPV Linear Parameter-Varying
LTI Linear and Time-invariant System
LKA Local Key-Account
1 前言
智能车辆的纵、横向跟踪控制技术是自动驾驶技术的基础,也是自动驾驶领域的重点和难点,跟踪控制技术的好坏直接决定智能车辆的性能[1-3]。
国内外学者对此进行了广泛且深入的研究。文献[3-5]针对纵向跟踪问题,采用模型预测控制理论(Model Predictive Control,MPC)设计了综合考虑车辆多性能指标的自适应巡航控制算法(Adaptive Cruise Control,ACC),并研究了解决控制算法低鲁棒性和非可行解的问题,提出了改进方法。文献[6-7]针对新能源车辆的纵向跟踪问题,提出了一种改进的ACC控制算法,运用非线性模型预测控制理论(Nonlinear Model Predictive Control,NMPC)实现了车速的优化控制,利用仿真及硬件在环验证了控制器的时效性。文献[8-9]针对横向跟踪问题,考虑跟踪精确性和行驶稳定性约束,提出了具有良好稳定性能的路径跟踪控制器。文献[10]针对路径跟踪预瞄控制方法的普适性问题,采用粒子群优化算法(Particle Swarm Optimization,PSO)对预瞄距离进行自适应寻优,仿真和硬件在环测试表明自适应预瞄距离能够满足不同工况下的控制要求。文献[11]针对路径跟踪控制问题,综合纯跟踪算法与多点预瞄模型,将预瞄偏差转化为前轮转角控制量,并通过试验验证了控制算法的有效性。
上述研究多为分散式控制,即通过对纵、横向运动进行解耦,把轨迹跟踪问题分解为纵向运动控制和横向路径跟踪问题。由于车辆的纵、横向状态存在强非线性和强耦合性,当极限工况下车辆的非线性特性和动力学耦合增强时,分散式控制难以保证良好的跟踪性能。本文从系统整体角度出发解决轨迹跟踪控制问题,充分地考虑纵、横向运动控制间的耦合特性,设计了基于自适应模型预测控制理论的轨迹跟踪控制器,通过主动控制前轮转角和加速度实现车辆的横向和纵向控制。考虑了车辆运动学耦合特性的影响,以纵向速度作为调度参数,引入车辆线性变参数系统模型(Linear Parameter-Varying,LPV),通过对控制器内部预测模型参数化处理,更新控制器的状态来适应车辆行驶环境变化。分析预测时域内的约束条件和代价函数,将跟踪控制问题转化为了预测时域内的二次规划问题,获取控制器的输入,从而实现车辆的轨迹跟踪。
2 轨迹跟踪车辆动力学模型
针对弯曲道路上对前车的轨迹跟踪控制问题,考虑对横向位姿跟踪和纵向速度和距离跟踪。如图1所示,前车沿弯曲道路中心线行驶,曲线o2o3为前车的行驶轨迹,ve、vl为自车和前车车辆的质心速度,srea、sdes、Δs为frenet 坐标系so2d 下的车间实际距离、期望距离和距离误差;Δy、Δψ、为车身坐标系xo1y下的横向位置误差和航向角误差。
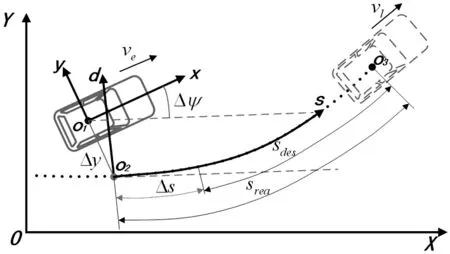
图1 轨迹跟踪误差示意
纵向跟踪分为对车间期望距离的跟踪和设定速度的跟踪,车间期望距离模型如下:

式中,τe为车间时距;s0为车辆静止时的距离;ve为自车质心速度。
可以得到纵向跟踪误差的表达式:

式中,vr为引导车速度vl或设定速度vset;srea为车间实际距离;sdes为车间期望距离。当未检测到引导车辆时,即对实时规划轨迹跟踪时,srea=sdes。
纵向跟踪的状态空间表示如下:
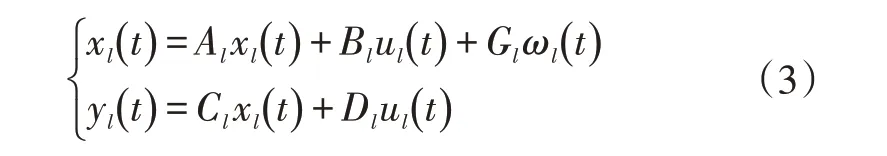
式中,
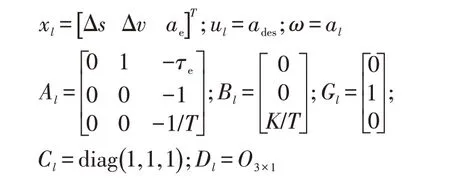
其中,Δs为距离跟踪误差;Δv为速度跟踪误差;ae为自车加速度;ul为控制输入(自车期望加速度);ωl为可测干扰(前车加速度)。
横向跟踪包括横向位置和方向角的跟踪,对于已知的期望路径,横向跟踪的状态空间表示如下:

式中,

其中,Δy为横向位置误差;Δψ为航向角误差;ur为控制输入(前轮转角δ);ωr为可测干扰(期望横摆角速度ψdes=ρve,ρ为期望轨迹曲率)。


其中,cf、cr分别为前后轮的侧偏角刚度;m车身质量;lr、lf分别为前后轴到质心的距离;Iz为车身绕z轴旋转的转动惯量。
3 轨迹跟踪控制器设计
3.1 预测模型
式(4)为线性时不变系统(LTI),未能考虑纵、横向耦合特性,因此为考虑纵向速度变化,采用线性变参数系统(LPV)对控制问题进行描述,并把纵向速度变化引入预测模型中,不断更新状态工作点,对系统模型进行线性化。把纵向速度作为调度参数(Scheduling parameters),LTI模型中的常数状态空间矩阵Ar、Gr转化为参数化状态空间矩阵Ar(ve)、Gr(ve),即a22、a24、a42、a44、g21、g21会跟随调度参数的变化而变化。
从调度参数取值范围中选取有限个点组成等间距的队列:

式中,vemin、vemax分别为车辆速度的下、上限,n为调度空间中选取的点的数量,在选取的每一个节点上,建立对应的LTI模型:

式(6)代表了n 个LTI 模型,用以表示在节点附近局部范围内的状态变化,并通过相邻点处的线性插值来获得调度参数节点之间的调度位置状态矩阵,以此获得模型的状态变化。例如,当k时刻的调度参数满足如下条件:
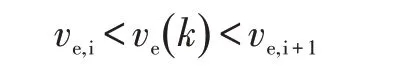
k时刻状态矩阵Ar即为:

综上,即可用式(6)的LTI 模型的插值队列来表示横向跟踪过程中速度发生变化时的LPV 模型。在线性控制过程中,调度参数ve可以由实时的控制输入和被控对象状态得到:
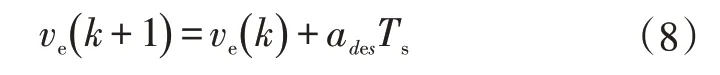
式中,Ts为仿真步长。根据调度参数的实时反馈,实现状态空间矩阵Ar(ve)、Gr(ve)的自适应变化。
联合式(3)、式(6)建立轨迹跟踪模型,并以Ts作为离散步长得:

式中,k代表当前时刻;
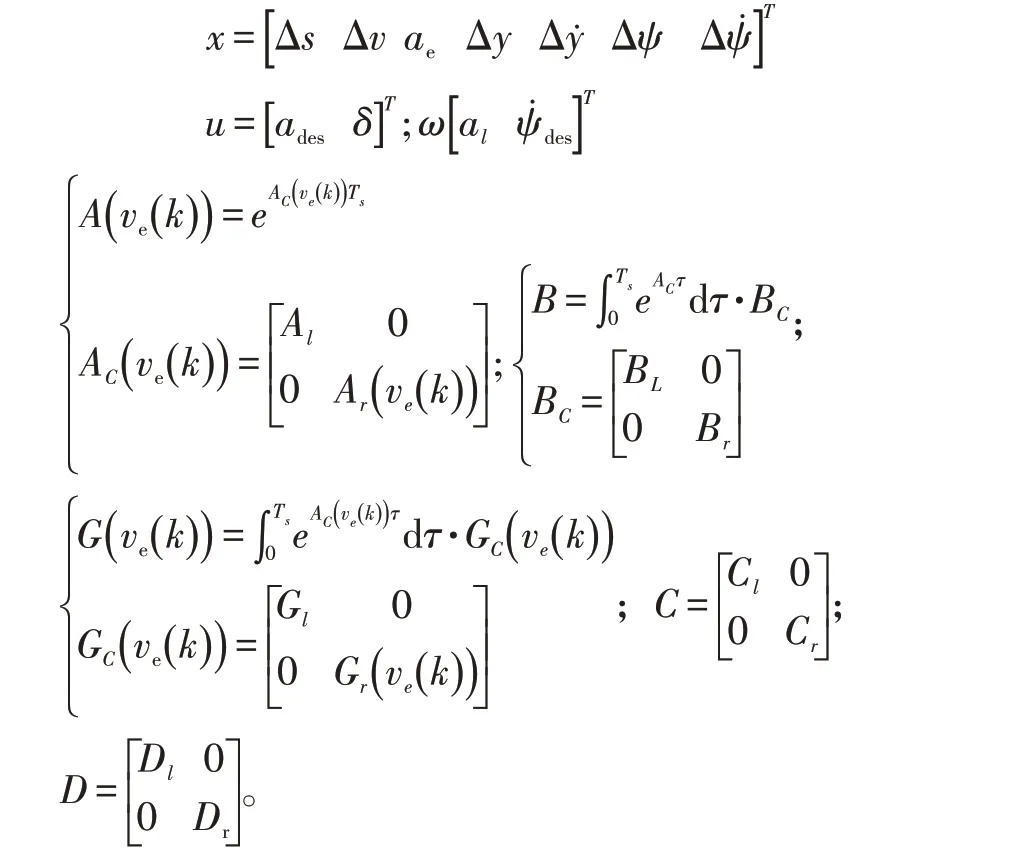
控制目标为y=[0 0 al0 0 0 0]T,控制输入为ae和δ,和al为干扰输入。
3.2 滚动优化
在轨迹跟踪过程中,模型的状态量、控制量及其变化率需要满足如下的约束条件:

式中,vmax为最高车速;amax、amin为车辆加速度的上、下限;W为车道宽度,lw为轮距;u为路面附着系数;δmax为前轮最大转向角;m、n分别为预测时域内状态量和控制量受约束的时域长度,以p作为预测时域,q 作为控制时域,预测模型可由离散化状态空间模型式(7)得到。为了保证约束效果同时提高运算速度,m、n的取值应满足:

m、n 取值越小,运算的实时性越好,用于每个循环预测时域内优化计算的代价函数包括3个部分:跟踪误差代价Je、控制量代价Ju和控制量的变化率代价JΔ。
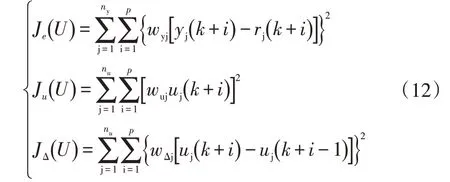
式中,U=[u ( k )…u( k+1)]T,为控制序列;ny、nu分别为输出量和控制量的维度;wyj、wuj、wΔj分别为每一项的权值;
综上,即把轨迹跟踪控制问题转化为如下的二次规划问题:

式中,
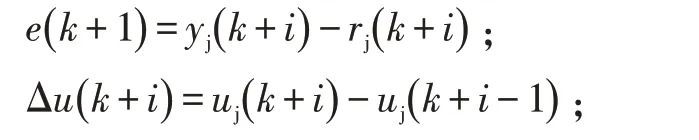
Q、R、RΔ、E、L、M由式(9)、(11)推导得出。
在线控制时,对当前预测时域内进行式(13)的优化求解,得到最优控制序列,运用序列的第一项进行控制,然后向前推进一步,对下一步重复此操作。式(13)同时考虑了横向跟踪和纵向跟踪控制问题,由于纵、横向状态的强耦合关系,引入了LPV模型,把纵向速度对横向跟踪的影响转化为LPV 模型中调度参数的变化,把纵、横向跟踪的高度非线性动力学模型转化为LTI 模型的插值队列,这样既可让预测模型自适应调度参数的改变,又可在保证跟踪效果的同时有效降低计算量。
4 仿真验证
为验证轨迹跟踪控制器的性能,基于MATLAB/Simulink 和MATLAB/Automated Driving Toolbox 搭 建了仿真验证平台。分别针对车道跟随(LKA+ACC)工况和已知换道轨迹跟踪工况进行仿真验证。车辆参数如表1所示。
4.1 车道跟随
图2 所示为一条S 形道路,自车跟随引导车辆从左向右行驶,跟踪过程中,引导车辆沿道路中心线行驶,同时速度呈正弦曲线变化(图3),仿真结果如下。

表1 车辆主要参数

图2 S形道路
从图3、图4 可以看出,对于纵向的速度距离跟踪,控制器能够很好的适应,速度误差控制在±1.5 m/s,纵向跟踪误差控制在±1.5 m,既确保了跟踪性能也保证了行驶安全。

图3 纵向跟踪结果
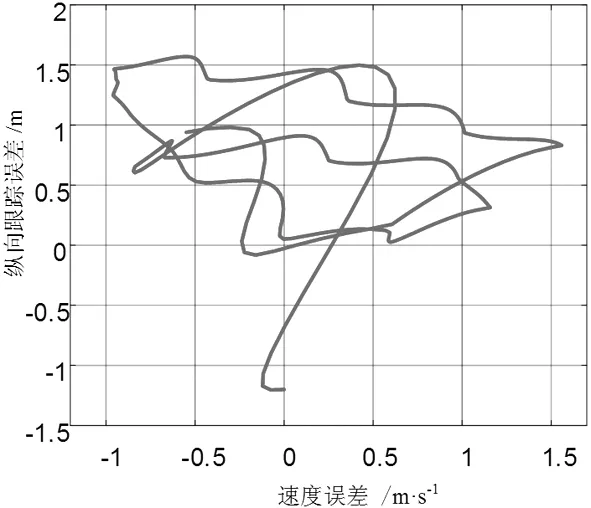
图4 纵向跟踪误差像
从图5、图6 可以看出,对于横向跟踪,自车的横向偏移和航向角偏移均控制在很小的范围内,且控制器能够很好的自适应自车速度的变化,保证了横向跟踪的精确性。

图5 横向跟踪结果

图6 横向跟踪误差
4.2 换道轨迹跟踪
参考一条已规划好的换道轨迹:
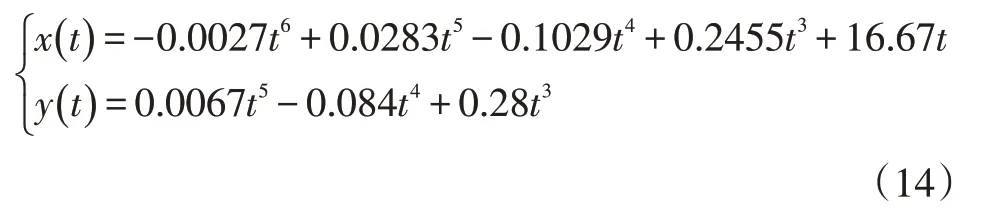
式中,x、y为横纵坐标;t为时间,已规划的总换道时间为4.5 s。
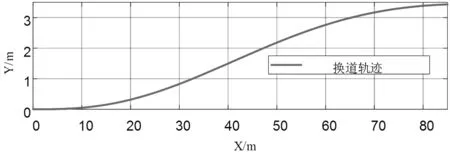
图7 规划轨迹
由式(14)得到如图8 的一条换道轨迹,其不仅包含几何路径信息还包含时间(速度)信息。对其进行跟踪仿真,结果如如图8 所示,其中蓝色虚线为式(7)规划轨迹中包含的期望速度信息,从结果中可以看出控制器能够基本保证速度跟随,但存在一定的偏差,是因为在高速状态下换道时,为了确保安全,控制器会重点考虑横向跟踪,同时适当地降低车速。

图8 纵向跟踪结果
图9 、图10所示为横向跟踪结果和误差,其中横向轨迹跟踪误差被控制在较小的范围内,表明控制器能够很好的完成高速状态下的轨迹跟踪控制,确保行驶安全。
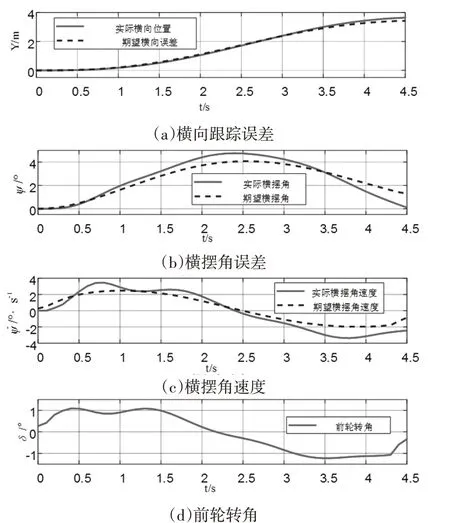
图9 横向跟踪结果
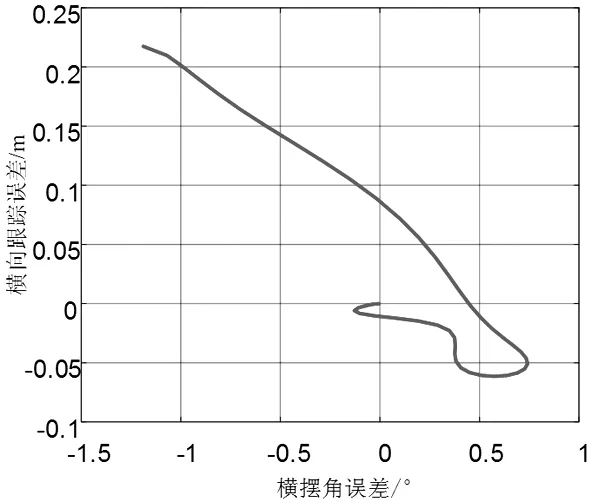
图10 横向跟踪误差
5 结论
(1)本文针对智能车辆的纵、横向跟踪控制问题,设计了自适应模型预测轨迹跟踪控制器。首先为解决纵、横向控制的强非线性问题,设计了轨迹跟踪LPV 模型,把纵向速度作为调度参数,使预测模型的状态空间矩阵能够自适应地改变。
(2)考虑跟踪过程的跟踪性能和安全性因素,建立了预测时域内的代价函数和约束条件,将跟踪控制问题转化为每个预测时域内的二次规划问题。
(3)仿真验证了控制器在车道跟踪和轨迹跟踪中的有效性,在保持跟踪精度的同时还有效提高了行驶稳定性。
