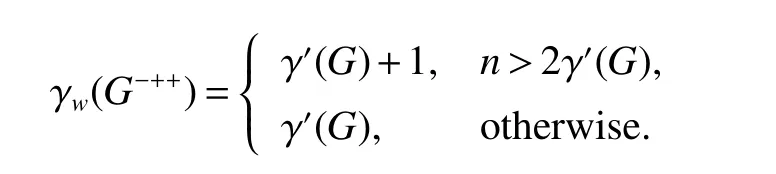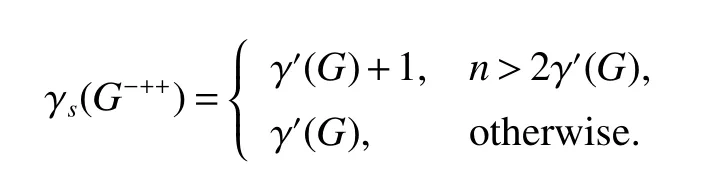Total Transformation Graphs Gxyz∗

LI Yaping,WU Baoyindureng

(School of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)

Abstract: Let G=(V(G),E(G))be a simple undirected graph of order n and size m,and x,y,z be three variables taking value+or −. The transformation graph Gxyz of G is the graph with vertex set V(G)∪E(G)in which the vertex α and β are joined by an edge if one of the following conditions holds: (i) for α,β ∈V(G), and αβ ∈E(G) if x=+, and αβ ∉E(G) if x=−, (ii) for α,β ∈E(G),and α and β are adjacent in G if y=+,and α and β are not adjacent in G if y=−,(iii)one of α and β is in V(G)and the other is in E(G),and they are incident in G if z=+,and α and β are not incident in G if z=−. The transformation graph Gxyz was first introduced by Wu and Meng in 2001,as the variation of the total graph. Since then,a large number of works are devoted to investigate various kinds of properties of these transformation graphs. In this paper, we summerize the results and unsolved problems on Gxyz.

Key words: total graph;total transformation graphs;complements;graph parameters

0 Introduction

LetG=(V(G),E(G))be a simple undirected graph. We refer to[1,2]for unexplained terminology and notations. For a vertexvofG,thedegree of vinGis denoted bydG(v). Theneighbourhoodofv,denoted byNG(v)is{u∈V(G)|uv∈E(G)}.Thedistance dG(u,v)between two verticesuandvinGis the length of a shortest path between them.

The symbols Δ(G), δ(G), κ(G), λ(G), α(G), α′(G) and ω(G) denote the maximum degree, the minimum degree, the connectivity, edge-connectivity, the independence number and the cardinality of a maximum matching ofG, the clique number, respectively. The connectivity (resp. edge-connectivity) ofG, denoted by κ(G) (resp. λ(G)), is defined to be the largest integerkfor whichGisk-connected(resp.k-edge connected). Δ′(G)=max{dG(u)+dG(v)|uv∈E(G)}.

ThecomplementofG, denoted by, is the graph with the same vertex set asG, in which two vertices are adjacent if and only if they are not adjacent inG. The line graph ofG, denoted byL(G), is the graph with vertexE(G), in which two vertices are adjacent if and only if they are adjacent as the edges inG. Thetotal graph T(G)ofGis the graph whose vertex set isV(G)∪E(G),and in which two vertices are adjacent if and only if they are adjacent or incident inG.

LetG=(V(G),E(G))be a graph,and α,β be two elements ofV(G)∪E(G). We say that the associativity of α and β is+if they are adjacent or incident inG. Letxyzbe a 3-permutation of the set+,−. We say that α and β correspond to the first termx(resp. the second termyor the third termz)ofxyzif both α and β are inV(G)(resp. both α and β are inE(G),or one of α and β is inV(G)and the other is inE(G)).

Thetransformation graph GxyzofGis defined on the vertex setV(G)∪E(G). Two vertices α and β ofGxyzare joined by an edge if and only if their associativity inGis consistent with the corresponding term ofxyz. Since there are eight distinct 3-permutations of+,−, we obtain eight graphical transformations ofG. It is interesting to see thatG+++is exactly the total graphT(G)ofG,andG−−−is the complement ofT(G). Also,for a given graphG,G++−andG−−+,G+−+andG−+−,G−++andG+−−are other three pairs of complementary graphs.

The transformation graphGxyzwas first introduced by Wu and Meng[1]in 2001,as the variation of the total graph. All these transformation graphs turn out to bear some nice properties.

1 Basic properties

We useeuvto denote the vertex inGxyzfor an edgeuv∈E(G). Wu and Meng[1]give a necessary and sufficient condition forGxyzbeing connected for a graphG. For eachxyz,Gxyzturn out to have good connected property.

Theorm 1(Wu and Meng[1])For a given graphG,G+++is connected if and only ifGis connected.

Theorm 2(Wu and Meng[1]) For a given graphG,G++−is connected if and only ifGhas at least two edges, andG2K2.

Theorm 3(Wu and Meng[1])For a given graphG,G+−+is connected if and only ifGcontains no isolated vertices.

Theorm 4(Wu and Meng[1])For a graphG,G+−−is connected if and only ifGhas at least two edges.

Theorm 5(Wu and Meng[1])For any graphG,G−++is connected.

Theorm 6(Wu and Meng[1])For a graphG,G−+−is connected if and only ifGis not a star.

Theorm 7(Wu and Meng[1])For any graphG,G−−+is connected.

Theorm 8(Wu and Meng[1])For a graphG,G−−−is connected if and only ifGis neither a star nor a triangle.

2 Diameter

Interestingly,for a graphG,ifGxyzis connected,its diameter is not large(not exceed 4),except the case whenxyz=+++.

Theorm 9(Wu and Meng[1])IfGis connected,

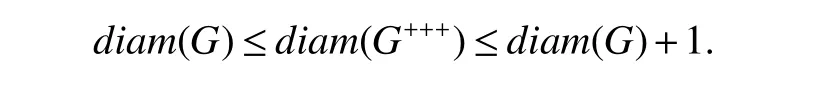
Theorm 10(Wu and Meng[1])IfGhas at least two edges,andG2K2,then

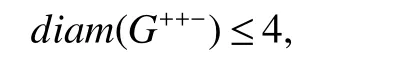
with quality if and only ifG2K2∪mK1,m>0.

Theorm 11(Wu and Meng[1])IfGhas no isolated vertices,then

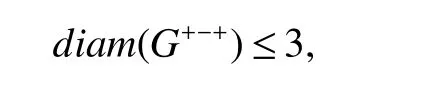
with equality if and only ifGis isomorphic to a disjoint union of two stars.

Theorm 12(Wu and Meng[1])IfGhas at least two edges,then

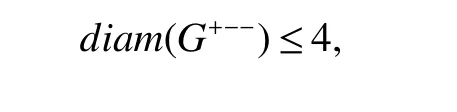
with equality holds if and only ifGP3.

Theorm 13(Wu and Meng[1])LetGbe a graph,then

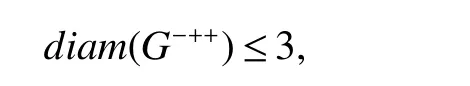
with equality if and only ifdiam(L(G))>2.

Theorm 14(Wu and Meng[1])IfGis not a star,thendiam(G−+−)≤3.

Theorm 15(Wu and Meng[1])For any graphG,diam(G−−+)≤3, with equality if and only ifGcontains a triangle,which has a vertex of degree two inG.

Theorm 16(Wu and Meng[1])IfGis neither a star nor a triangle,thendiam(G−−−)≤3.

3 Regularity

It is clear that a graphGis regular if and only ifis regular. Lin and Shu[3]present a necessary and sufficient condition forGxyzbeing regular.

Theorm 17(Lin and Shu[3])For a graphG,G+++andG−−−are regular if and only ifGis regular.

Theorm 18(Lin and Shu[3])For a connected graphGof ordern≥3,G++−andG−−+are regular if and only ifGCnorK2,n−2orK4.

Theorm 19(Lin and Shu[3])For a graphGof ordern≥2 and sizem,G+−+andG−+−are regular if and only ifGC5orK2orK7orK3,3orC3□K2.

Theorm 20(Lin and Shu[3])For a graphGof ordernand sizem≥1,G−++andG+−−are regular if and only ifGisregular.

4 Planarity

A graph is said to be embeddable in the plane, or planar, if it can be drawn in the plane so that its edge intersect only at their ends. Such a drawing is called planar embedding of the graph. The well-known Kuratowski’s theorem[4]states that a graph is planar if and only if it contains no subdivision of eitherK5orK3,3.

All the following theorem is deduced from the Kuratowski’s theorem. For two graphsGandHwithV(G)∩V(H)=∅,G+Hdenotes their disjoint union.

Theorm 21(Behzad[5])The total graphG+++of a graphGis planar if and only if Δ(G)≤3 and every vertex of degree 3 is a cut vertex.

Theorm 22(Yuan and Liu[6])For a graphG,G++−is planar if and only if either|E(G)|≤2 orG∈{C3,C3+K1,P4,P4+K1,P3+K2,P3+K2+K1,K1,3,K1,3+K1,3K2+K1,3K2+2K1,C4,C4+K1}.

Theorm 23(Wang and Liu[7]) LetGbe a graph of sizem, ThenG+−−is planar if and only if eitherm≤2 orGis isomorphic to one of the following graphs:C3,C3+K1,P4,P4+K1,P3+K2,P3+K2+K1,K1,3,K1,3+K1,3K2,3K2+K1,3K2+2K1,C4,C4+K1,2P3.

Theorm 24(Wu,Zhang,Zhang[8])For a graphG,G−++is planar if and only if|V(G)|≤4.

Theorm 25(Wang[9])For a graphG,G−+−is planar if and only ifn≤4 andGis not isomorphic toK4−e.

Theorm 26(Wang[9]) For a graphG,G−−+is planar if and only if eithern≤3 orGis isomorphic to one of the following graphs: 2K1+K2,K1+K1,2,K1,3,K1+C3.

Theorm 27(Liu[10])LetGbe a graph of ordern,ThenG−−−is planar if and only if eithern≤3 orGis isomorphic to one of the following graphs: 2K2,C4,K4−e,K4,2K+K3,K1,4,K1+K1,3,2K1+P3.

The only case whenxyz=+−+remains to be solved.

5 Isomorphism

Gr¨unbaum[11]formulated two fundamental problems for any graphical transformations, which can be stated forGxyzas follows: Determination problem. Determine which graphs have a given graph as theirGxyz. Characterization problem.Characterize those graphs that areGxyzfor some graph.

Theorm 28(Wu and Meng[1])For a graphG,

(i)G+yzGif and only ifGis an empty graph;

(ii)G−yzGif and only ifGK1.

Theorm 29(Wu,Zhang,Zhang[8])For two graphsGandG′,G−++G′−++if an only ifGG′.

Theorm 30(Wu,Zhang,Zhang[8])For two graphsGandG′,G+−−G′+−−if an only ifGG′.

Conjecture 1(Wu,Zhang,Zhang[8])For two graphsGandG′,G++−G′++−if an only ifGG′.

Conjecture 2(Wu,Zhang,Zhang[8])For two graphsGandG′,G+−+G′+−+if an only ifGG′.

Characterization problem forGxyzremains to be open.

6 Hamiltonicity,Connectivity and Independence number

6.1 Hamiltonicity

LetGbe a graph. A cycle ofGis called a Hamilton cycle if it contains every vertex ofG. A graph is called hamiltonian if it contains a Hamilton cycle. A well-known theorem of Chv´atal and Erd˝os[12]states that if a graphGof order at least 3 is hamiltonian κ(G)≥α(G).

EPS-subgraphs were first introduced by Fleischner in[13].An EPS-subgraph of graphGis a connected spanning subgraphSwhich is the edge-disjoint union of a(not necessarily connected)graphE,all of whose vertices have even degree,with a(possibly empty)forestPeach of whose component is a path.

Theorm 31(Fleischner and Hobbs[14])LetGbe a finite graph with at least 2 vertices. Then the total graphG+++ofGis hamiltonian if and only if G contains an EPS-subgraph.

Most of the following theorems for the Hamiltonicity ofGxyzare deduced from the above theorem of Chv´atal and Erd˝os.

Theorm 32(Ma and Wu[15])LetGbe a graph. ThenG−−−is hamiltonian if and only ifGis not isomorphic to any graphs in{K1,r|r≥1}∪{K1,s+K1|s≥1}∪{K1,t+e|t≥2}∪{K2+2K1,K3+K1,K3+2K1,K4}.

Theorm 33(Wu,Zhang,Zhang[8])For a graphGof ordern,G−++is hamiltonian if and only ifn≥3.

Theorm 34(Xu and Wu[16])For a graphGof ordern≥4,G−+−is hamiltonian if and only ifGis not isomorphic to any graph in{K1,n−1,K1,n−1+e,K1,n−2+K1}∪{2K1+K2,K1+K3}.

Theorm 35(Zhen and Wu[17])For a graphGwith no isolated vertices,G+−−is hamiltonian if and only ifGis neither a star,norG∈{2K2,K3,K1,1}.

Theorm 36(Yi and Wu[18])LetGbe a graph of ordern≥6 and sizem. Ifm≥α(G)+1,G++−is hamiltonian.

Corollary 1(Yi and Wu[18])LetGbe a graph of ordern≥6 and sizem. Ifm≥n,G++−is hamiltonian.

6.2 Connectivity

Theorm 37(Sim˜oes-pereira[19])

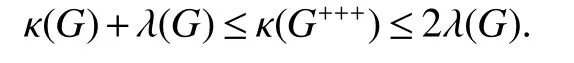
The lower bound improves one the previously obtained as follows:

Theorm 38(Hamada and Nonaka and Yoshimura[20])

Theorm 39(Bauer and Tindell[21])If λ(G)≥2,then λ(G+++)=δ(G+++)=2δ(G).

Theorm 40(Zhang and Huang[22])For a given graphG,κ(G+−+)=δ(G+−+)if and only if none of the following three conditions apply:

(1)Ghas at least two components,one of which isK2,and δ(G)≥1;

(2)Ghas at least two components,one of which isK3,and δ(G)≥2;

(3)GK1,n.

Corollary 2(Zhang and Huang[22])IfG2K2,then λ(G+−+)=δ(G+−+).

Theorm 41(Xu and Wu[16])For a graphGof ordernand sizem,κ(G−+−)=min{δ(G−+−),n+κ(L(G))−min{δ(G−+−),n+κ(L(G)),m+κ()}.

Theorm 42(Yi and Wu[18])For a graphGof ordern≥6 and sizem≥3,κ(G++−)≥min{m−1,n+κ(L(G))−1}.

Corollary 3(Xu and Wu[16])For a graphGof ordern≥4,the following statements are equivalent:

(1)κ(G−+−)≥2;

(2)δ(G−+−)≥2;

(3)G∉{K1,n−1,K1,n−1+e,K1,n−2+K1}.

Corollary 4(Xu and Wu[16])For a graphGof ordern≥4,κ(G−+−)=2 if and only if δ(G−+−)=2.

Theorm 43(Zhen and Wu[17])For a graphGof orderpand sizeq,

6.3 Independence number

Lemma 1(Ma and Wu[15])For a graphG,we have α(G−−−)=3 if Δ(G)=1,and α(G−−−)=Δ(G)+1,otherwise.

Theorm 44(Ma and Wu[15])For any graphG,

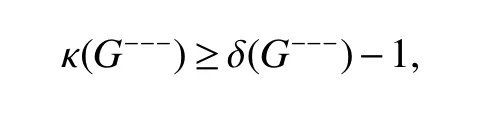
with equality if and only ifGcontains a triangle and Δ(G)=2.

Theorm 45(Xu and Wu[16])For any graphG,

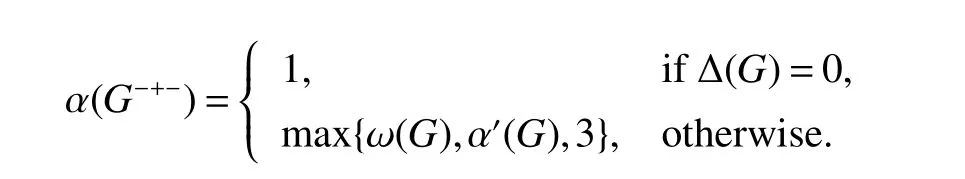
Theorm 46(Wu,Zhang,Zhang[8])For any graphG,λ(G−++)=δ(G−++).

Theorm 47(Zhen and Wu[17])For any graphG,

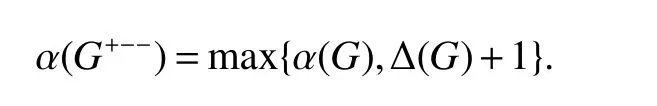
Theorm 48(Yi and Wu[18])For any graphG,

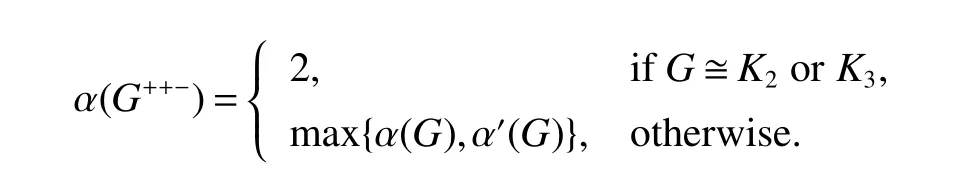
7 Super edge-connectivity and cyclic edge-connectivity

7.1 Super edge-connectivity

A graphGis said to be maximally edge-connected or simplyGis max−λ if λ(G)=δ(G). A graphGis said to be super edge-connected or simplyGis super-λ if for every minimum edge cutTofG,G−Thas isolated vertices.

Theorm 49(Chen and Meng[23])For a given connected graphG,G+++is super-λ if and only if one of the following two conditions holds:

(1)λ(G)≥2,ifGhas a cut vertexxwithdG(x)=δ(G),then there are 3 or more edges betweenxand any component ofG−x;

(2)λ(G)=1,ife=xyis a bridge,then min{dG(x),dG(y)}≥2δ(G).

Theorm 50(Chen and Meng[23])For a given connected graphGwhich contains no isolated vertices,G+−+is super-λ if and only ifGhas no isolated edges andGK1,n.

Theorm 51(Chen and Meng[23])For a given graphG,G−++is super-λ if and only ifGK1,norK1,n∪K1.

Corollary 5(Chen and Meng[23])For any graphG,λ(G−++)=δ(G−++).

Theorm 52(Chen and Meng[24])For any graphG,G−−+ismax−λ and thatG−−+is super-λ if and only ifGis neither isomorphic toK1,2norK2∪K1.

Corollary 6(Chen and Meng[24])For any graphG,λ(G−−+)=δ(G−−+).

Theorm 53(Chen and Meng[25])For a given graphGwhich has at least two edges,G++−is super-λ if and only if the follow ing conditions holds:

(1)G2K2∪mK1,K1,2∪mK1,K3∪mK1,2K3wheremis non-negative integer;

(2)GK2∪K3,K2∪P3,P4wherePiis a path of lengthi−1.

Corollary 7(Chen and Meng[25])IfGhas at least two edges andG2K2,2K2∪K1,K2∪P3,then λ(G++−)=W(G++−).

Theorm 54(Chen and Meng[26]) For a given graphG，G+−−is max-λ if and only ifGhas at least two edges andG2K2.

Theorm 55(Chen and Zhou and Huang[27])All the connected transformation graphsG−+−are max-λ.

Theorm 56(Chen and Meng[23])For a given graphG,ifG−−−is connected,then λ(G−−−)=δ(G−−−).

7.2 Cyclic edge-connectivity

LetGbe a connected graph. An edge-cut ofGis an edge-setF⊆E(G)such that there are at least two components inG−F. Cyclic edge-connectivitycλ(G)is the minimum cardinality over all the cyclic edge-cutF. Cyclic edge-cutFmeans that there are at least two components with cycles inG−F. For any cyclically separated graphGsatisfyingcλ(G)≤ϖ(G)[28],where ϖ(G)=min{ϖ(X)=[X, ¯X]:Xcan induces a shortest cycle ofG}.

Theorm 57(Chen, Zhu, Jiang[29])G++−is connected and cyclically separated if and only ifGcontains at least two edges,G≠2K2andG≠K1,2∪mK1,m≥0.

Corollary 8(Chen,Zhu,Jiang[29])G++−is connected and cyclically separated if and only ifGcontains at least three edges,orG=2K2∪mK1,m≥1.

Theorm 58(Chen,Zhu,Jiang[29])IfG++−be connected and cyclically separated,then

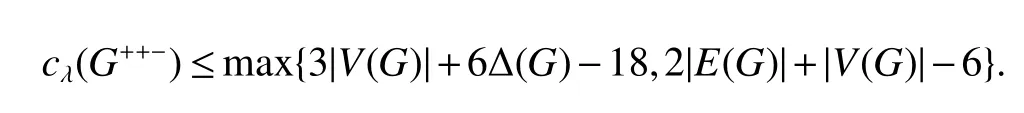
Theorm 59(Chen,Zhu,Jiang[29])LetGbe connected andG++−be connected and cyclically separated,then

8 Topological Indices

A molecular graph is obtained from a molecular by representing its atoms by vertices and its bonds by edges. Graph theoretic invariants of a molecular graph,which predict properties of the corresponding molecule,are known as topological indices.

8.1 Zagreb index

The first and second Zagreb indices are two oldest and well-known topological indices, which were introduced by Gutman and Trinajsticet[30]in 1972, where they have examined the dependence of the total π-electron energy on molecular structure. The first Zagreb and second Zagreb indices are respectively defined respectively as follows.

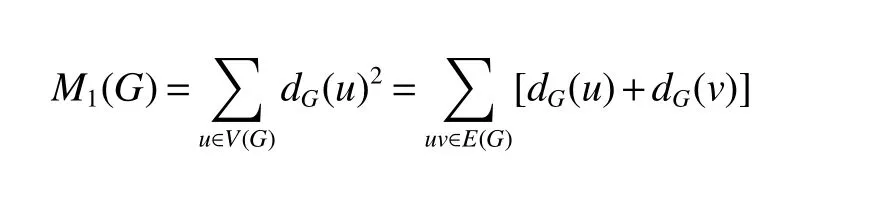
and

As the sums involved run over the edges of the complement ofG,such quantities were called Zagreb coindices,defined by Ashrafi[31]. More formally,the first and second Zagreb coindex of a graphGis defined as

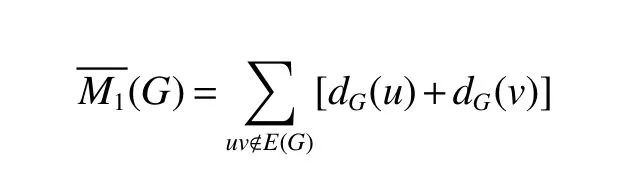
and

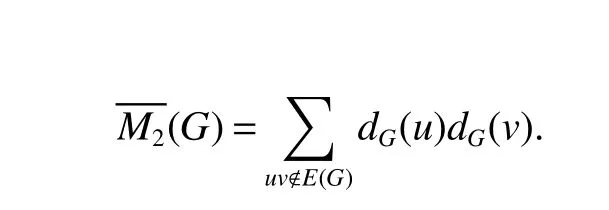
In[32],De defined

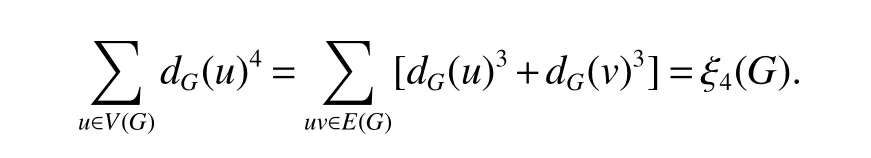
In[33],for a positive integerThen ξ1(G)is just twice the number of edges ofG,where as ξ2(G)is the first Zagreb index.

Theorm 60(Hosamani and Gutman[33])For a graphGof ordernand sizem,

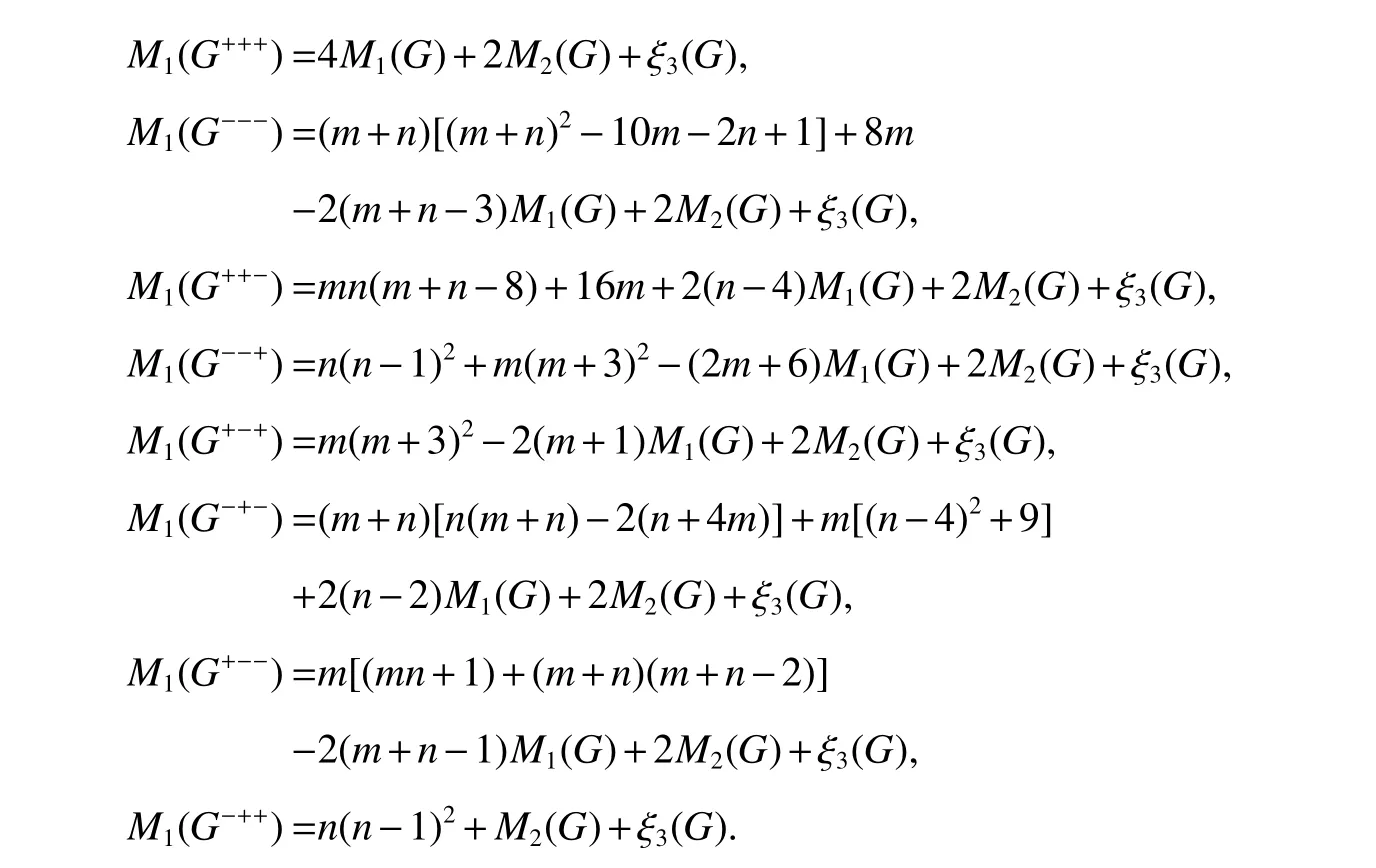
Corollary 9(Hosamani and Gutman[33])For a graphGof ordernand sizem,

8.2 F-index

A topological index[30]was also shown to influence total π-electron energy. This index was defined as sum of cubes of degrees of the vertices of the graph. Recently Furtula and Gutman[34]studied this index and established some basic properties of this index. They named this index as“forgotten topological index”or“F-index”,denote it byF(G),so

The redefined version of Zagreb indices of a (molecular) graph was introduced by Ranjini, Lokesha, and Usha[35]as follows:

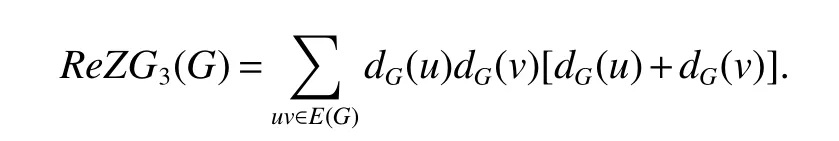
Theorm 61(De[32])For a graphGof ordernand sizem,

Theorm 62(De[32])For a graphGof ordernand sizem,

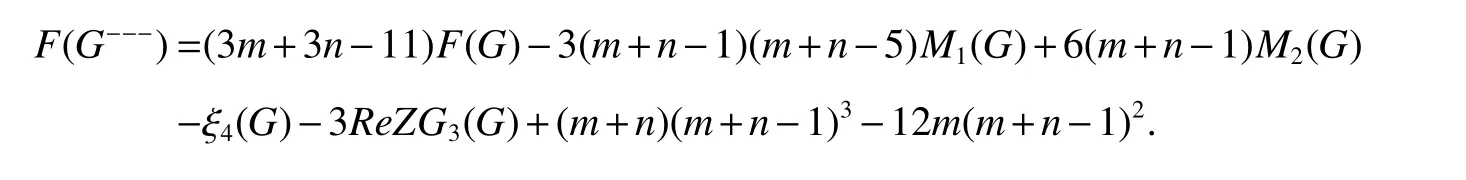
Theorm 63(De[32])For a graphGof ordernand sizem,

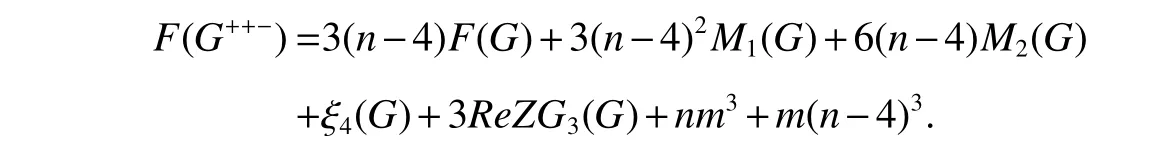
Theorm 64(De[32])For a graphGof ordernand sizem,

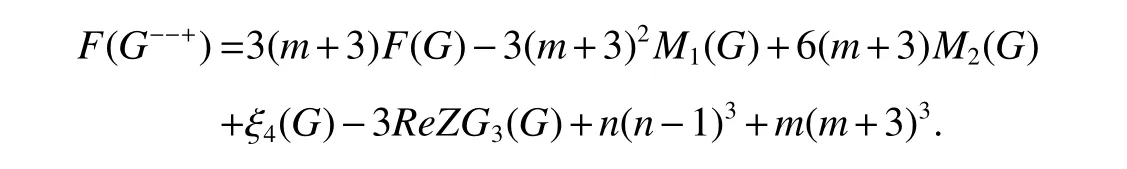
Theorm 65(De[32])For a graphGof ordernand sizem,

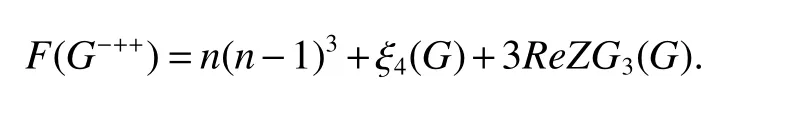
Theorm 66(De[32])For a graphGof ordernand sizem,

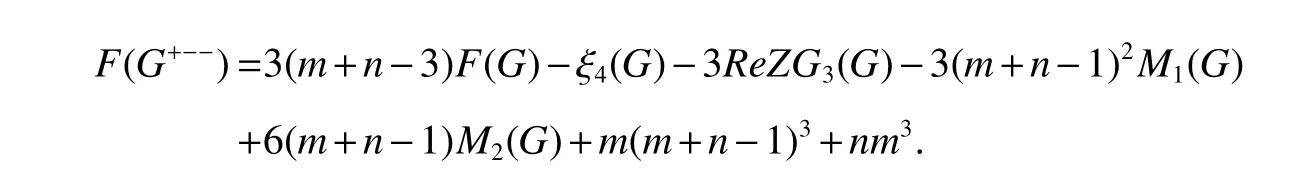
Theorm 67(De[32])For a graphGof ordernand sizem,

Theorm 68(De[32])For a graphGof ordernand sizem,

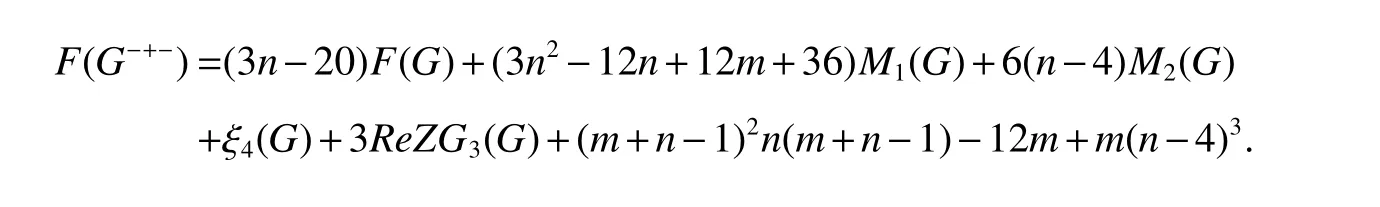
8.3 NK-index

In 1984,Narumi and Katayama[36]introduced a multiplicative graph invariant for representing the carbon skeleton of a saturated hydrocarbon, and named it as a “simple topological index”. Tomovic and Gutman[37]later renamed this index as“Narumi-Katayama index”or“NK index”and is denoted by NK(G).The Narumikatayama index of a graphGis defined as the product of degrees of all its vertices,that is

Eliasi, Iranmanesh and Gutman[38]introduced a new multiplicative graphical invariant and called multiplicative sum Zagreb index,which is defined as

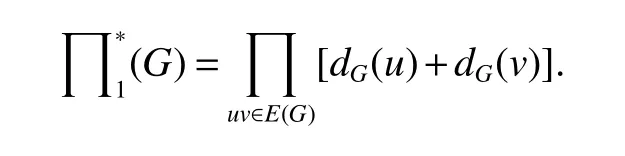
Theorm 69(De[39])For a graphGof ordernand sizem,

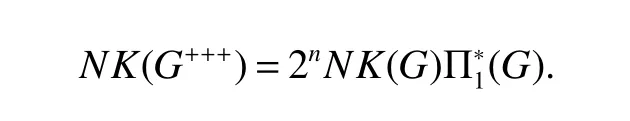
Theorm 70(De[39])For a graphGof ordernand sizem,

with equality if and only ifGbe a regular graph.

Theorm 71(De[39])For a graphGof ordernand sizem,with equality if and only ifGbe a regular graph.

Theorm 72(De[39])For a graphGof ordernand sizem,

with equality if and only ifGbe a regular graph.

Theorm 73(De[39])For a graphGof ordernand sizem,

Theorm 74(De[39])For a graphGof ordernand sizem,

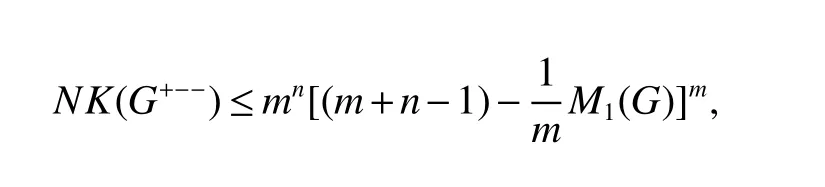
with equality if and only ifGbe a regular graph.

Theorm 75(De[39])For a graphGof ordernand sizem,

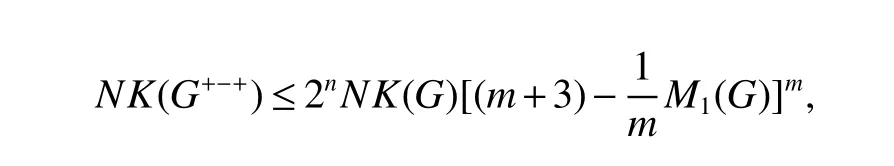
with equality if and only ifGbe a regular graph.

Theorm 76(De[39])For a graphGof ordernand sizem,

with equality if and only ifGbe a regular graph.

9 Spectra

The adjacency matrix ofGis then×nmatrixA(G):=(auv),whereauvis the number of edges joining verticesuandv.The characteristic polynomial of matrixA(G)is called the characteristic polynomial of the graphG,denoted byPG(λ).

Theorm 77(Cvetkovi´c and Doob and Sachs[40]) LetGbe a regular graph of degreer(> 1) havingnvertices andmedges, If the eigenvalues ofGare λ1≥λ2≥··· ≥λn, thenG+++hasm−neigenvalues equal to -2 and the following 2neigenvalues:

It can be obtained from the proof of the above theorem:

Theorm 78(Yan and Xu[41])LetGbe a regular graph of degreerhavingnvertices andmedges. If the eigenvalues ofGare λ1≥λ2≥···≥λn,then

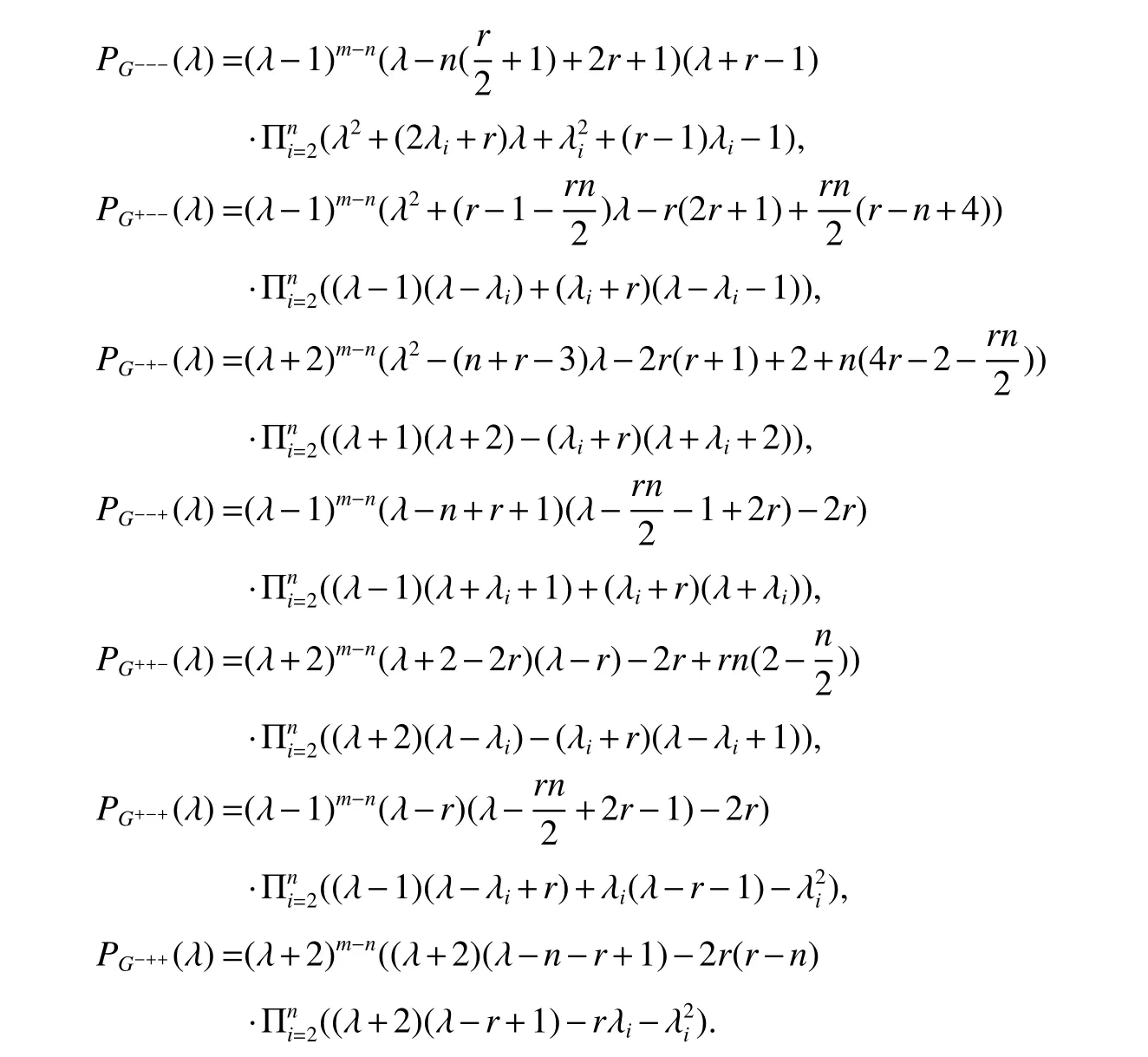
10 Spectral Radius

LetGbe a simple graph with ordernand letA(G)be the adjacency matrix ofG. The spectral radius ρ(G)ofGis defined as largest eigenvalue ofA(G).

Theorm 79(Lin and Shu[3])LetGbe a connected graph with ordern≥3 and sizem. Then

Theorm 80(Lin and Shu[3])LetGbe a connected graph with ordern≥2 and sizem≥2,andG≠2K2. Then

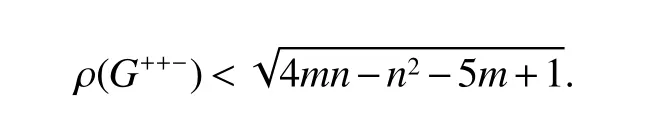
Theorm 81(Lin and Shu[3])LetGbe a connected graph with ordern≥3 and sizem. Then

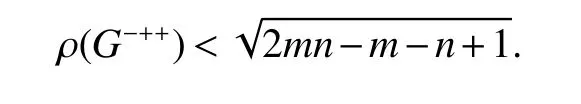
Theorm 82(Lin and Shu[3])LetGbe a connected graph with ordern≥2 and sizem,andGnot a star. Then

Theorm 83(Lin and Shu[3])LetGbe a graph with ordern≥3 and sizemand no isolated vertices. Then

Theorm 84(Lin and Shu[3])LetGbe a graph with ordern≥2 and sizemand no isolated vertices. Then

Theorm 85(Lin and Shu[3])LetGbe a graph with ordern≥3 and sizemand no isolated vertices. Then

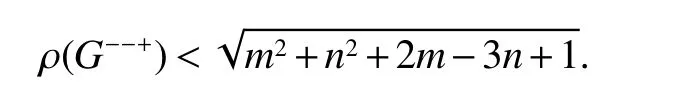
Theorm 86(Lin and Shu[3])LetGbe a graph with ordern≥3 and sizemand no isolated vertices,andGis neitherK3nor star. Then

11 Laplacian spectra

LetD(G):=(dij)be then×nmatrix,wheredii=dG(vi)anddij=0 fori≠j.The matricesD(G)andL(G)=D(G)−A(G)are called the degree matrix and the Laplacian matrix ofG,respectively. The Laplacian polynomial,the Laplacian spectrum and the Laplacian eigenvalues ofGare the characteristic polynomialL(λ,G)=det(λI−L(G)),the spectrum,and the eigenvalues ofL(G),respectively.

Theorm 87(Deng and Kelmans and Meng[42])Let G be an r-regular graph with n vertices and m edges. Then

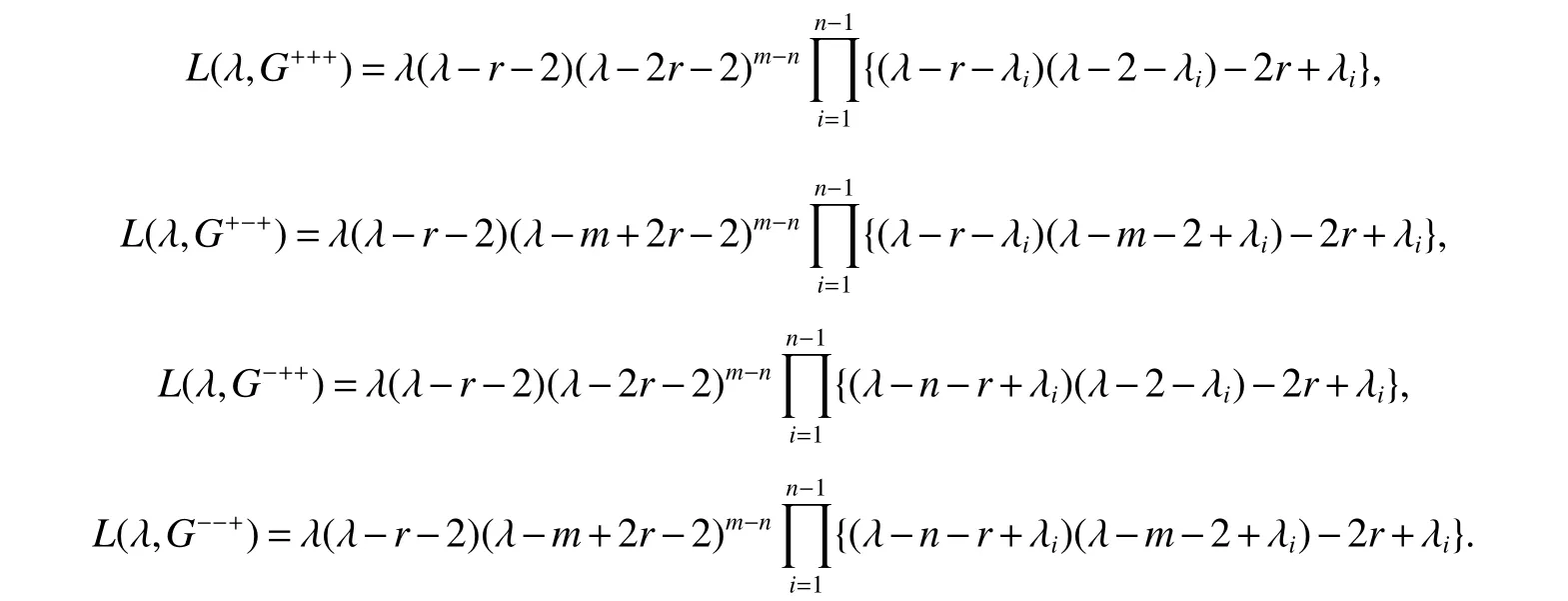
Theorm 88(Deng and Kelmans and Meng[42]) LetGbe anr-regular graph withnvertices andmedges and lets=n+m. Then

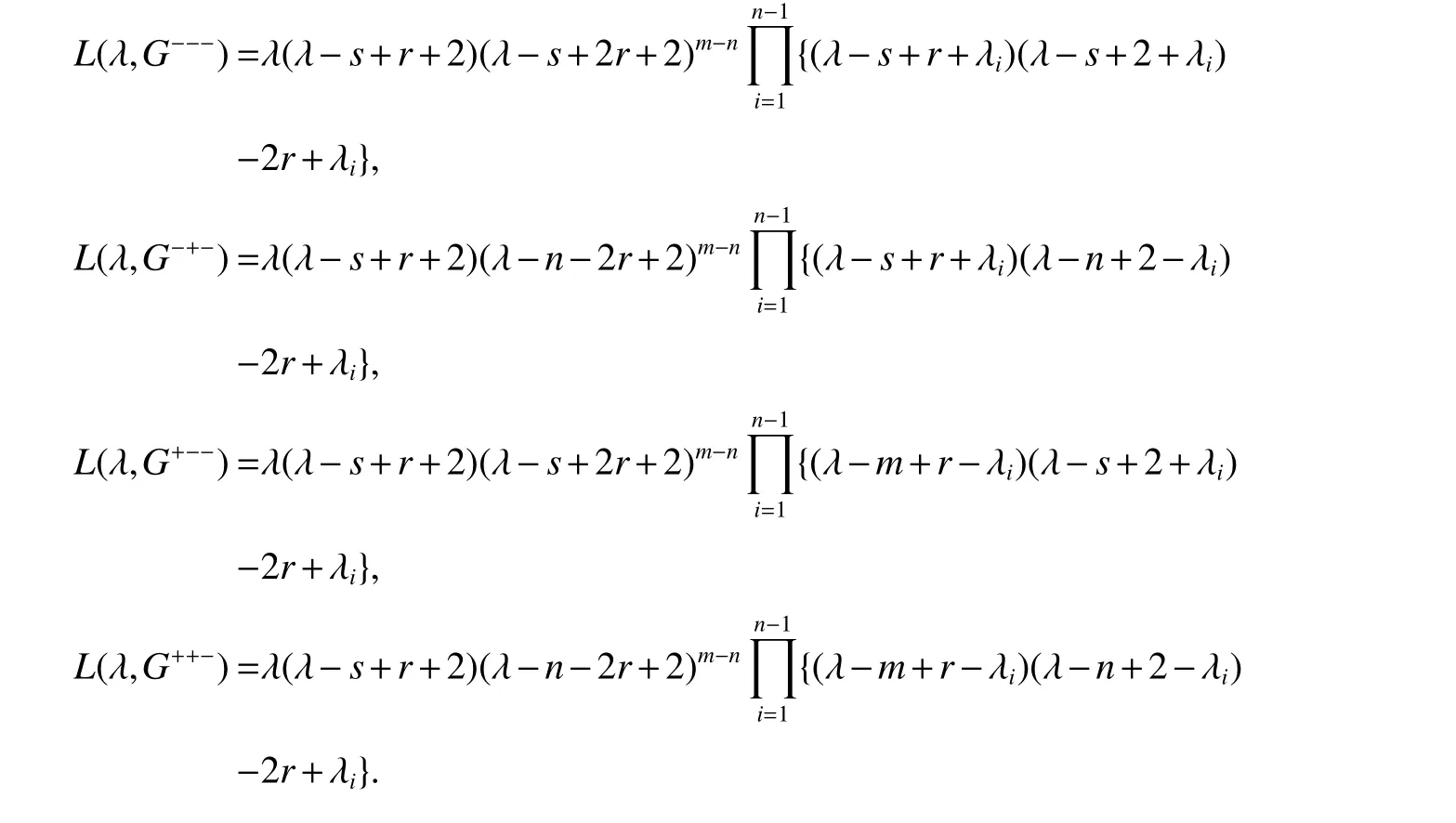
12 Domination

A vertex and edge are said to cover each other inGif they are incident inG. A vertex cover inGis a set of vertices that covers all the edges ofG. An edge cover inGis a set of edges that covers all vertices ofG. The minimum cardinality of a vertex cover in a graphGis called the vertex covering number ofGand is denoted by β(G). The edge covering number β1(G)ofGis the minimum cardinality of an edge cover inG.

A setS⊆V(G) is a dominating set if every vertex inV−Sis adjacent to at least one vertex inS. The minimum cardinality taken over all dominating sets ofGis called the domination number ofGand is denoted by γ(G). The concept of edge domination was introduced by Mitchell and Hedetniemi[43]. A subsetXofE(G)is called an edge dominating set ofGif every edge not inXis adjacent to some edge inX. The edge domination number γ′(G)ofGis the minimum cardinality taken over all edge dominating sets ofG[43].

Strong and weak domination was introduced by Sampathkumar and Latha[44]. Ifuv∈E(G),then u and v dominate each other. Further,ustrongly dominatesvandvweakly dominatesuifdG(u)≥dG(v). A setD⊆V(G)is strong dominating set(sd−set),if every vertexv∈V(G)−Dis strongly dominated by someuinD. The strong domination number γs(G)ofGis the minimum cardinality of asd−set. Similarly,a setW⊆V(G)is weak dominating set(wd−set),if every vertexv∈V(G)−Wis weakly dominated by someuinW. The weak domination number γw(G)ofGis the minimum cardinality of awd−set.

Aytac¸ and Turaci[45]obtained some bounds for the domination number ofGxy+. Jebitha and Joseph[46]presented some upper bound for the domination number ofG+−+. Jebitha and Joseph[47]determined the domination number ofG−+−for any graphG,by introducing a new parameter,calledindependent edge domination numberof a graphG(denoted by

Theorm 89(Aytac¸ and Turaci[45]) LetHbe a connected graph of ordernand includes only one pendant vertex. If graphG=H−euvof ordernand r-regular fordH(u)=1 andv∈NH(u),then

Theorm 90(Jebitha and Joseph[46])For any graphG,γ(G)≤γ(G+−+)≤γ(G)+2 and the bounds are sharp.

Theorm 91(Jebitha and Joseph[46])LetGbe a connected graph of ordern≥5. Then γ(G+−+)and the bound is sharp.

Theorm 92(Jebitha and Joseph[46])IfGis a connected graph with Δ(G)=n−2,then γ(G+−+)≤3.

Theorm 93(Jebitha and Joseph[46])If a graphGhasdiam(G)=2,then γ(G+−+)≤δ(G)+1 and the bound is sharp.

Theorm 94(Jebitha and Joseph[46])For any connected graphGwith Δ(G)

Theorm 95(Jebitha and Joseph[46])LetGbe a connected graph of ordern>2 with Δ(G)=n−1 andvbe a vertex of degree Δ(G). Then γ(G+−+)=2 if and only if〈N(v)〉is non-empty and it containsK1orK2or is isomorphic toK1,r,r≥2.

Theorm 96(Aytac¸ and Turaci[45])LetGbe a connected graph with ordernand sizem,γ(G−++)≤1+γ′(G).

Theorm 97(Aytac¸ and Turaci[45])LetGbe a connected graph with ordernand r-regular. Ifn>2r+1,then

Theorm 98(Aytac¸ and Turaci[45])LetGbe a connected graph with ordernand r-regular. Ifn<2r+1,then

Theorm 99(Aytac¸ and Turaci[45])LetGbe a connected graph with ordernand sizem,Then,γ(G+−+)≤β(G).

Theorm 100(Aytac¸ and Turaci[45]) LetGbe a connected graph with ordernand sizem, IfGincludes only one pendent vertex and maximum vertex degree Δ(G)=n−1,then γ(G+−+)=2.

Theorm 101(Aytac¸ and Turaci[45])LetGbe a connected graph with ordernand r-regular. Ifr>3,then γ(G−−+)=γw(G−−+)≤β(G)and γs(G−−+)≤n−β1(G).

Theorm 102(Jebitha and Joseph[47])For any graphG,γ(G−+−)≤3. Furthermore,

(i)γ(G−+−)=1 if and only if δ(G)=0;

(ii)γ(G−+−)=2 if and only ifdiam(G)≥3 orGhas a maximal matching of size 2.