路基回弹模量预估研究进展∗

李玲，艾贤臣

(新疆大学建筑工程学院，新疆土木工程技术研究中心，新疆乌鲁木齐830047)

路基土与粒料回弹模量是沥青路面设计的重要参数，也是路面结构应力-应变分析的必备输入参数，其准确与否将影响到路面结构组合设计、疲劳损坏预估状况及路面结构多层系统的力学响应分析．目前，回弹模量三轴试验方法是广为流行的测试方法，能较好的反映路基土回弹模量应力相关性，但三轴试验设备昂贵、操作复杂．所以，国内外许多学者在深入分析回弹模量主要影响因素（土组类型、应力状况、含水率、压实度）的基础上，基于应力状况和土组物性参数建立了回弹模量预估模型．本文在广泛调研国内外路基土与粒料回弹模量预估模型既有研究成果的基础上，将各类预估模型进行了详细的归纳和总结，并对各类模型的优缺点、适用条件等进行了探讨．

1 本构预估模型

路基土与粒料的回弹模量本构模型经历了一个由简单到复杂的发展过程，大致可以分为两大类：一类是基于回弹模量及回弹泊松比的模型，包括仅考虑剪切影响的模型、仅考虑侧限影响的模型和复合类模型；另一类是基于体-剪分解法的复合模型，即所谓的K- G类模型．

1.1 基本参量

MR为回弹模量，µR为回弹泊松比，表示变化量，σ1是最大主应力，σ2为中间主应力，σ3是最小主应力，ε1R为轴向回弹应变，ε3R为径向回弹应变．

剪切影响表征参数一般包括偏应力σd或八面体剪应力τoct．

侧限影响表征参数一般包括最小主应力(围压应力)σ3，体应力(第一应力不变量)，平均正应力（八面体正应力）．

1.2 基于回弹模量及回弹泊松比的模型

1.2.1 仅考虑剪切影响的模型

土性不同，其应力应变状态受应力条件敏感性不同．对于细粒含量高、塑性指数高的粘性土，其强度主要来源于粘结力，摩阻力贡献非常小，因而侧限约束也即偏应力影响显著，其典型预估模型为：

1. 双线性模型(Bilinear Model)[1]

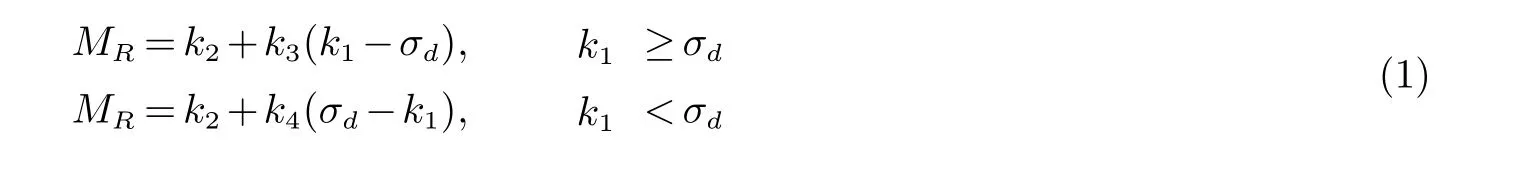
2. 半对数模型(Semi-log Model)[2]

3. 双曲性模型(Hyperbolic Model)[3]

4. 幂指数模型(Power-law Model)[4]

该类模型主要优点是参数简单、易于确定、应用方便．但其共同不足是仅体现主应力和围压的共同作用，未充分体现围压这一主要影响因素．因而该模型对于浅层细粒土较适用．随着土层深度的增加和荷载的增大，侧限应力也即围压对回弹模量的影响愈来愈显著，因而必须考虑．同时，很多学者通过研究提出，大多数细粒土的回弹模量随围压的增加有较大的增长，如图1所示[5]．在最大主应力与最小主应力之比超过2.5时，土一般都会呈现扩胀性状，故在荷载较重或者路基深度较大处，对粘性土回弹模量仍有必要考虑围压的影响．

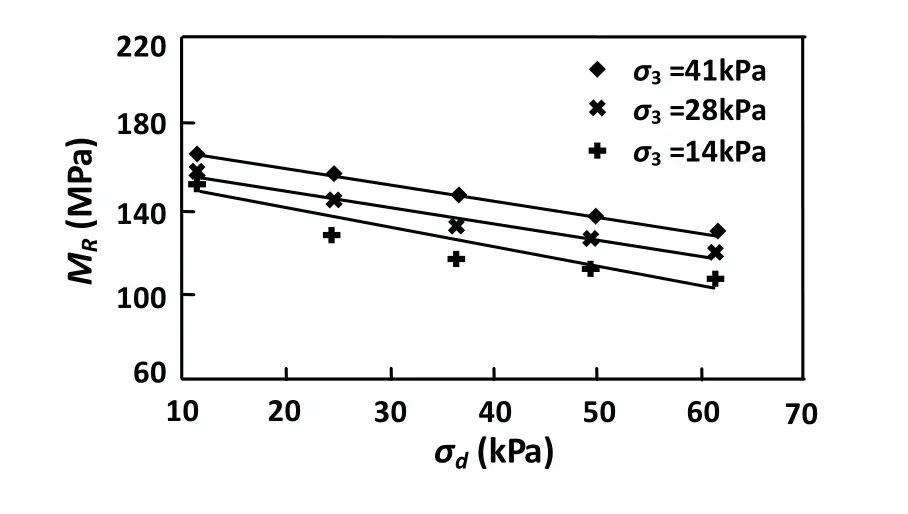
图1 粘性土(A-6)回弹模量试验结果Fig 1 Test results of resilient modulus of cohesive soil (A-6)

1.2.2 仅考虑侧限影响的模型

对于无粘性土和粒料性土，强度主要由摩阻力提供，粘聚力贡献则非常小，其回弹模量通常采用如下两种预估模型：

1. 围压模型[6,7]

2. K-θ模型

Seed等[8]、Brown和Pell[9]及Hicks和Monismith[10]建议将回弹模量表达为体积应力(主应力和)的函数：

K-θ模型是一种典型的反映路基材料强度本构属性的预估模型，尤其是碎砾石材料，至今仍被广泛使用．随后有很多学者直接或间接基于K-θ模型，构建了很多这类模型．其优点与幂指数模型一样，形式简单、参数确定容易、应用方便．但其也存在一些不足：

（1）这类模型仅考虑主应力和体应力对回弹模量的影响，而忽视了剪应力的重要影响[11]，不能合理地体现材料在最大主应力比条件下的膨胀行为，所以仅在非常有限的应力路径范围可采用该模型表征，其它应力路径可能会得出错误的预估结果；

（2）这类模型假设泊松比为常数，尽管能够较好预估轴向应变，但对径向应变和体应变预估结果较差；

（3）这类模型仅体现体应力状态下的回弹属性，且认为体应力相等时，回弹属性相同；同时也不能反映围压和偏应力对回弹模量的真实影响；

（4）这类模型还存在量纲不统一的问题．

1.2.3 复合模型

由上述两类模型分析可知，其共同缺点在于仅考虑了体应力或偏应力对材料回弹模量的影响．事实上，大部分路基土的回弹模量受应力路径影响显著，尤其是围压和剪应力，回弹模量既随围压增大而增加，也随剪应力增大而减小．因此回弹模量不仅与体应力密切相关，也应是偏应力或剪应力的函数．因此，很多学者将体应力和剪应力引入回弹模量预估模型中，进而考虑综合影响，可以更真实、全面地反映土与粒料的力学性状．

基于此，学者们建立了复合模型．典型的预估模型有Uzan模型、八面体剪应力模型、Superpave性能模型、Ni模型等．具体预估模型如下：

1. Uzan模型

该模型是最基本的复合模型，其它很多复合模型以此为基础进行修正后提出．该模型克服了K-θ模型没有考虑剪应力影响的缺陷，而是充分考虑了应力路径对材料回弹行为的影响．

Boudali和Rober[12]通过三轴试验，选择了5种粒料且每种粒料选取6个级配，对预估模型进行了验证，结果表明，K-θ模型的预估偏差为±25%，而Uzan模型的预估偏差为±16%，后者优于前者．由于Uzan模型中既包含了体应力，又包含了偏应力，因而该模型既适用于应力软化材料，也适用于应力硬化材料．鉴于其优点及参数简单、易于确定，Uzan模型可用于柔性路面设计．该模型的缺点在于：

（1）仍然无法实现量纲统一；

（2）当σd=0时，MR→0；当σ1=σ3=0，MR=0·∞，故而存在模量不定值问题；

（3）路基土的泊松比仍为假设常数，通常取µ=0.3．

2. 八面体剪应力模型

与Uzan模型相比较，两个模型具有相同的拟和精度（σd与τoct成比例）．八面体剪应力模型消除了量纲问题，但仍存在模量不定值问题．

3. Superpave性能模型

美国战略公路研究计划SHRP使用的性能模型如式(9)：

当k4=0，即为NCHRP 1-28A[13]推荐的模量预估模型：

Andrei等[14]选用6种材料（基层粒料、路基粗粒土和细粒土各2种）进行了25个三轴试验，比较了13种基于回弹模量及回弹泊松比的本构模型与实测数据的吻合程度．对比结果显示，K-θ模型的预估精度最差，且八面体剪应力模型的预估精度不如superpave性能模型．

4. Ni模型

考虑到围压对路基回弹模量影响显著，Ni[15]等引入围压和偏应力对Uzan模型进行修正，得出如下的回弹模量预估模型：

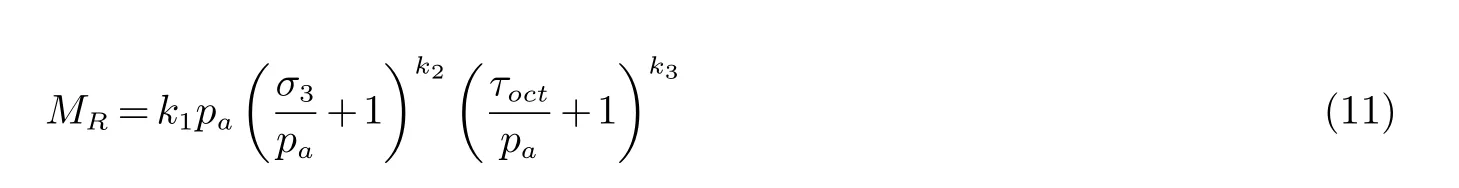
NCHRP1-28A模型和Ni模型不仅提高了精度，而且通过引入大气压和常数项，还解决了量纲和模量不定值的问题．但比较Ni模型和NCHRP1-28A模型，第一项中前者选择围压做控制变量，而后者选择体应力做控制变量，此外Ni模型在第一项中还多引入了一个常数项，这就使得Ni模型在低应力级位时，可获得更高的模量定值性，因此可提高其在低应力级位下的数值稳定性．

5. 修正的Ni 模型

冉武平[16]在研究黄土路基回弹模量时发现，黄土回弹模量对湿度也非常敏感，而且在不同的湿度条件下，对不同的应力状态敏感性不同，鉴于此，基于Ni 模型，提出了不同湿度下的修正模型：

该模型的最大优势在于充分考虑了湿度对路基回弹模量影响，进而提高了预估的精度．

1.3 K-G类本构模型

K-G类本构模型的构建思想是将应力与应变分解成体变分量和剪切分量，并以回弹体积模量K与剪切模量G作为模型参数，表征材料的应力-应变关系，这是与之前的本构模型最大不同之处．Brown和Hyde[17]通过研究提出，以K与G为参数表征颗粒性材料的非线性优点如下：

（1）避免分析过程的线弹性假设；

（2）在分析应力与应变时，可分别处理体变分量和剪切分量；

（3）通过三维应力状态分析，具有比回弹模量和泊松比更直接、实际的物理意义．

1. Boyce 模型（K-G Model）

Boyce遵循Maxwell互逆定理(即认为没有应变能净损失)，结合对级配良好的石灰岩碎石重复加载三轴试验结果，提出了基于割线体积模量与割线剪切模量的体-剪模型，如式（14）所示．

Boyce模型对于表征材料的非线性性状更真实，主要体现在：该模型可以正确模拟应力路径高q/p对回弹性状的剪胀影响；同时亦可分别描述体积应变和剪切应变随平均正应力p的非线性增长影响，以及应力比q/p增加时剪切应变增长，体积应变减小的规律[18]．

Maxwell互逆定理明确了体应变和剪应变的关系，故而仅需明确η，Ki和Gi3个参数即可定义模型．由于该模型的线弹性假设对于预估塑性特性较显著的未处治粒料的非弹性响应存在明显缺陷．故要得到预估结果很好的K-G模型，需严格遵循互逆定理．事实上，由于重复加载三轴试验中加载与卸载阶段存在能量消散，故而其应力-应变曲线不重合．Sweere[19]的研究进一步指明体-剪模型的预测值与实测体应变之间有较大的差异．基于此，Sweere为使体应变与剪应变成为相互独立的量，建议去除模型的弹性假设，也即互逆定理的限制，并为此得到了较好的拟合效果．

2 经验预估模型

经验预估模型是基于三轴试验和相关基本理论基础上构建的，与本构模型相比使用简单，参数测定方便．然而基于本构关系，还兼顾了许多土组因素的经验公式，既考虑嵌入了应力路径又考虑了土的物性参数，实用性很强值得借鉴．但这类模型由于试验工况有限，因而使用有其局限性，使用时需考虑边界条件与公式建立条件的相似性．

2.1 基本参量

2.1.1 模量参数

MR或ER为回弹模量（MR通过室内重复加载三轴试验测定，ER在现场测定，MPa或psi ）；EFWD为现场FWD弯沉盆反算回弹模量（MPa或psi）；ELFWD为轻型落锤弯沉仪测定的回弹模量（MPa或psi）；EGeo为土刚度仪测定的回弹模量（MPa或psi）．

2.1.2 强度参数

qu为无侧限抗压强度（UCS，kPa或psi）；CBR为加州承载比；PR为动力锥贯入试验（DCP）所测得的贯入率，亦即动力锥贯入指数（mm/blow或in/blow）．

2.1.3 应力参数σd为偏应力（kPa或psi）；σ3为围压应力（kPa或psi）；σoct为八面体正应力（kPa或psi）；τoct为八面体剪应力（kPa或psi）；θ为体应力（kPa或psi）；Pa为大气压（一般取100 kPa或14.7 psi）．

2.1.4 土组参数

S为饱和度（%），ω为含水量（%），ωopt为最佳含水量（%），LL为液限（%），PL为塑限（%），PI为塑性指数，cu为均度系数，P200为0.075 mm筛的通过百分率，γd为干密度（kN/m3或pcf），γdmax为最大干密度（kN/m3或pcf）；%clay为粘粒（<2 μm）百分含量，%silt为粉粒（2～7.5 μm）百分含量，%sand为砂粒（0.075～2 mm）百分含量．

2.2 基于力学指标的关系式

2.2.1 Heukelom & Klomp公式

Heukelom与Klomp[20]根据Shell公司的现场动模量测试结果及其他若干公开数据回归得到如下线性关系式：

式(15)中未考虑应力路径，回归系数α变动范围为5～20之间，并取安全系数为2，如图2所示．关于α取值，相关学者和研究机构给出了建议值，一般取10；而AI MS-1提出(15)式仅限于回弹模量低于207 MPa的工况的预估；AASHTO路面结构设计指南（1986, 1993）则规定式(15)仅适用于浸湿路基土的CBR≤10的细粒土．相关研究表明，CBR≤20时，ER=10CBR所得结果回归精度较高，即该预估模型对细粒土与细砂土都适用[21]．

图2 ER CBR关系图(引自AI)Fig 2 ER CBR diagram (from AI)

2.2.2 USACE公式(U.S. Army Corps of Engineers)

Green 和Hall[22]通过AASHTO试验路段，再结合其他若干区域已知基层、底基层及路基材料CBR的测点处震波技术测试相关结果，提出USACE公式：

文献[22]指出，该模型提出原始CBR在2～200之间取值，但依然未考虑应力路径．

2.2.3 SSV相关[23]

LDOTD(路易斯安那州交通研究部)采用AASHTO路面结构设计指南（1993）进行路面设计时，提出了用SSV（土基支撑值）预估路基回弹模量，如下式所示：

2.2.4 DCPI相关[21]

Gudishala[23]提出回弹模量与DCPI（锥贯入指数）与土的物性参数之间的经验预估模型：

（1）粘性土：

（2）粒料土：

该模型中引入力地基的强度指标，在很大程度上完善了回弹模量与地基承载力之间的关系．

2.3 基于物性指标的关系式

2.3.1 USDA (美国农业部)模型

该模型是Carmichael和Stuart[24]针对细粒土，选用了250多种土的3 300个土样，开展回弹模量试验提出的细粒土回弹模量预估模型，如式（20）所示．此模型中，进一步表明土的粒组和性质是影响模量的关键因素，同时该模型也考虑了偏应力对模量的影响．

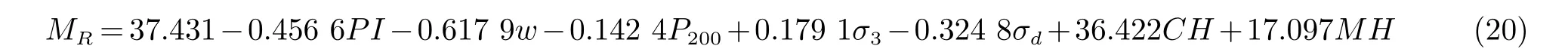
2.3.2 Tennessee Model2

Drumm等[25]以基于双曲线回弹模量预估模型为基础，选择了Tennessee 的11种典型土，开展回弹模量试验，提出了如下的回弹模量预估模型：

其中：m=318.2+0.333qu+0.73(%clay)+2.26PI−0.915γd−2.19S−0.304P200,n=2.1+0.000 39/a+0.104qu+0.09LL−0.1P200.

2.3.3 Northern Indiana 模型

Lee[26]通过北印第安纳的砂的回弹模式试验研究，提出了该州沙丘砂的回弹模量经验预估模型：

式中：RC为沙丘砂的相对压实度，一般取95%～103%．

3 吸力相关预估模型

由于路基土在运营阶段的水汽迁移，致使路基在绝大数情况下都处于非饱和状态．对于非饱和土，由于基质吸力的影响，使土的力学性质，尤其是应力应变特性明显有别于饱和土．鉴于此，有很多学者认为，基质吸力是反映非饱和土通过湿度状态变化的重要指标，尤其是在土-水特性曲线中反映显著．故而基质吸力不仅反映土的应力应变特性，同时可以进一步反映湿度状况对于回弹模量的影响．

Brown[27]通过考虑路基上覆层自重引起的平均正应力和轮载引起的偏应力的应力影响状态，而忽略随路基深度增加，自重应力增大，轮载作用效应减小的影响，提出了用式（23）来表征粘性路基土的非线性回弹响应．Loach[28]在Brown的研究基础上，选取了更具有代表性的路基土样开展了三轴试验，并提出修正式（24）．

式(23)(24)是通过在三轴试验仪的室压应力和土吸力模拟上覆层自重引起的有效平均正应力，开展三轴试验．其中a的取值为20～200 MPa，b的取值为0～0.5，c的取值为10～100，d的取值为1～2，qR为汽车荷载引起的偏应力．

Ceratti等[29]通过对巴西南部页岩残余红土的室内试验土水特性曲线与回弹模量关系现场测试的基质吸力与回弹模量关系的试验研究，得出基质吸力对该土回弹模量的影响规律．进而提出了回弹模量和基质吸力回归模型，如式（25）所示：

式中：μa-μw为土吸力（kPa）．尽管现场测试的基质吸力变化幅度非常小，但对回弹模量影响却非常显著．

Parreira[30]选定巴西非常典型的红土路基填料，开展了非饱和状态下的回弹模量试验，通过实验总结了回弹模量与偏应力和总吸力之间的规律，并提出了预估模型，如式（26）所示：

张世洲[31]在已有研究成果的基础上，构建了全面考虑湿度、围压、偏应力和基质吸力等因素的路基土回弹模量经验预估模型，如式（27）所示：

钱劲松[32]基于Fredlund和Vanapalli等的思路，以饱和度Sr衡量基质吸力贡献比例，并用系数k进行修正，提出考虑基质吸力的非饱和细粒土动态回弹模量预估方程：

4 结论

（1）路基土的回弹模量预估模型就构建思想而言，主要分为本构模型、经验公式以及考虑基质吸力的非饱和土预估模型．从工程应用的角度而言，经验公式具有参数求解方便、计算简便和实用性强的特点．但这类公式适用条件严格，局限性强，适宜于符合条件的现场测试和计算；而本构模型则具有普适性强、计算结果理论依据强，但是大多需要通过试验分析才能确定相关参数，应用成本较高，适宜于设计阶段的回弹模量计算分析；考虑基质吸力的预估模型，属于精细化分析范畴，但测试参数和试验条件更多，工程应用不方便，适宜于精细化的力学响应分析．

（2）本构模型可以分为两大类：一类是基于应力路径和土体泊松比参数，仅考虑土体受力的应力状态的模型；另一类是基于体-剪分解法的K-G复合模型，即以回弹体积模量K与剪切模量G作为模型参数．从本构机理上分析，第二类模型具有更好的拟合精度和物理意义，尤其是表征土体的非线性优势更加明显；但这类模型形式过于复杂，参数确定困难，工程应用性差一些．而第一类模型参数确定方便，工程应用经济实用．

（3）由于不同土体在运营阶段，对湿度的敏感性不同，建议细粒土采用考虑湿度的预估模型，避免本构模型不考虑湿度或者将之与应力状况分割开来的缺陷；粗粒土或沙土对湿度敏感性低，则可直接采用仅考虑应力状态的预估模型，从而简化公式，增强工程应用性．