基于相对风暴径向速度场的辐合区自动识别算法

竹 利 康 岚

1)(高原与盆地暴雨旱涝灾害四川省重点实验室，成都 610072) 2)(四川省南充市气象局，南充 637006) 3)(四川省气象台，成都 610071)

引 言

中层径向辐合(mid-altitude radial convergence,MARC)为对流风暴中层(通常为3～9 km高度)的径向辐合区，用以反映由风暴前侧的强上升入流气流和风暴后部入流急流(rear inflow jets，RIJ)之间的过渡区[1]。Lemon等[2]研究发现，在一个产生下击暴流的超级单体中，下沉气流与上升气流的交界面附近存在一深厚辐合区，Lemon等[3]在另一个产生地面大风的超级单体中也发现类似深厚辐合区，并推断与深层辐合相伴随的气流加速和负的浮力共同作用产生地面大风。国内学者们的研究也表明，在强对流大风天气过程中常伴有中层径向辐合特征[4-12]。当天气雷达的多普勒径向速度图上存在明显MARC特征时，预示地面将会产生灾害性大风，MARC特征的参数信息(强度、高度等)对地面大风天气临近预警具有较好指示意义[13-14]。一般径向辐合在对流层3～7 km高度上的2～6 km径向距离范围内出现25 m·s-1以上径向速度差，认为MARC 特征显著[15]。有研究表明[16-17]，显著MARC特征对地面大风预警的提前时间为10～30 min。因此，强风暴中深厚辐合带的探测和识别对地面大风预警起重要作用。

MARC强度在一定程度上表征飑线系统后部干冷空气卷入雷暴体内的激烈程度，夹卷越激烈，越有利于冷池的发展，从而产生更强的地面大风[3]。因此，MARC与地面大风之间可能存在相关关系。利用MARC特征自动识别算法可对大量历史个例的雷达资料进行批量计算，经过统计分析计算结果，揭示其中关系。利用高空间分辨率雷达资料，判别地面大风的强度，对未布局地面观测站区域的对流性大风监测预警以及灾害评估，提供参考依据。另外，强天气系统雷达回波特征的自动识别，可提高灾害天气的短时临近预报水平[18-20]。MARC特征自动识别及特征参数的计算对辅助业务人员分析天气系统也起着积极作用，提前识别该特征有利于提升预警信号发布时间提前量。因此，MARC自动识别算法有较大实际业务应用价值。MARC特征在平均径向速度图中常表现为一对相邻且面积相当的正速度区和负速度区，称为典型“正-负速度区域对”径向辐合特征[21]。王萍等[21]设计一种基于典型“正-负速度区域对”的MARC特征自动识别算法，该算法可识别出部分风暴的三维径向辐合特征。但对于强风环境影响下形成的对流系统，其径向辐合区有时表现为不对称的“正-负速度区域对”，有时甚至仅表现为单一正或负速度区域，称为非典型“正-负速度区域对”径向辐合特征[22]。这种情况下，基于典型“正-负速度区域对”的MARC特征识别算法难以识别出径向辐合区。因此，肖艳姣[22]提出另一种自动识别算法，该算法采用二维局地 LLSD(linear least squares)方法计算径向速度的径向散度切变，并使用类似SCIT(storm cell identification and tracking)算法的风暴单体径向辐合区识别算法进行风暴单体三维径向辐合区的自动识别。该算法可有效识别非典型“正-负速度区域对”径向辐合特征，但在计算径向辐合强度方面存在一定不足。由于散度切变是根据径向速度与距离权重乘积建立关系，往往速度最大值所在位置与径向辐合处有一定距离，若计算径向辐合强度所取二维局地窗口的径向长度小于正-负速度大值中心之间的距离，计算的径向辐合强度较实际值偏小。

本文对2016年8月6日一次具有非典型“正-负速度区域对”径向辐合特征的飑线过程开展研究，分析非典型“正-负速度区域对”径向辐合特征形成的原因。根据分析结果，本文提出将对流风暴的整体径向速度场减去风暴移动速度(朝向雷达为负，远离雷达为正，下同)后，得到相对风暴的径向速度场，在此基础上搜索雷达某径向上的“正-负速度区域对”，从而识别MARC特征。本文将该MARC特征识别算法称为相对风暴中层径向辐合特征(storm-relative mid-altitude radial convergence,SRMARC)识别算法。

1 假设条件及资料说明

本文在算法研究和设计过程中的假定和处理原则：①因天气雷达扫描的仰角较低，忽略垂直气流(或粒子落速)的影响，雷达测到的降水粒子径向速度即为实际水平气流的径向速度；②忽略单体风暴的移向和移速，只考虑整体风暴的移向和移速，且风暴整层的移速相同；③模式输出的风暴结构风场与实际风场一致；④以雷达的某径向为处理单元，使得径向辐合特征在风暴移向与风暴所在雷达径向一致时最明显，当风暴整体移向与风暴所在雷达径向的夹角小于20°时，假定风暴移向与风暴所在雷达径向一致；⑤为了获取3～8 km高度范围内完整的径向速度数据，算法只处理径向距离大于30 km且小于150 km范围，且强度大于40 dBZ和径向速度绝对值大于0.5 m·s-1(忽略弱对流系统)的距离库。

本文所用资料包括四川盆地地区2009—2018年10次飑线大风天气过程的常规观测资料、雷达资料(四川省气象探测数据中心提供)。另外，本文采用WRF4.0对2016年8月6日飑线个例进行模拟，模拟区域采用二重双向嵌套，水平分辨率分别为16.0 km和3.2 km，垂直方向为33层。网格中心位于30.0°N，104.5°E。长波辐射采用RRTM方案，陆地选取Noah方案，边界层选取YSU方案，短波辐射采用Dudhia方案，粗网格模拟区域采用Kain-Fritsch积云对流方案而非微物理方案，细网格模拟区域只采用 WDM6类微物理方案而非积云对流参数化方案。初始场为NCEP FNL分析资料。模拟初始时间为2016年8月6日14：00(北京时，下同)，积分24 h。

2 典型个例分析

中小尺度天气系统的流场结构由自身运动和平移运动共同构成，基本径向速度场主要是自身水平运动和平移运动综合影响的结果。当系统的平移运动速度大于自身运动速度时，系统在基本径向速度场上的切变(旋转、辐合或辐散)特征可能被掩盖[23]。由于MARC特征在对流层中高层表现较为显著，一般出现在正、负径向速度交汇区，且正速度区较负速度区距离雷达站更近。但在强风环境影响下形成的对流系统(如飑线)，其径向辐合区常表现为单一正或负速度区域内径向速度大小突变形成的径向辐合特征。在冷涡后部较强偏北气流影响下，2016年8月6日傍晚至7日凌晨四川盆地中部地区出现一次强飑线天气过程。图1a和图1d分别为该飑线过程在6日23:34乐山雷达3.4°仰角上的反射率因子及其沿径向(图1a黑色直线)的反射率因子剖面图。此时飑线以约40 km·h-1的速度沿径向朝雷达方向快速移动，造成地面灾害性大风。由径向速度图(图1b)及其剖面图(图1e)可知，该风暴南段(图1b中剖面线以南部分)2～5 km高度上均为一致的负速度区域(最大径向速度绝对值约23.0 m·s-1，表明对流系统存在后部入流急流特征)，但负径向速度从飑线后侧至前侧存在显著的径向速度辐合特征(负速度值突增)。该MARC即为非典型“正-负速度区域对”的MARC特征，利用王萍等[21]设计的MARC自动识别算法无法正确识别。

图1 2016年8月6日23:34乐山雷达3.4°仰角反射率因子(a)、原始径向速度(b)以及处理后的相对风暴径向速度图(c)及对应沿黑色直线的反射率因子剖面图(d)、径向速度剖面图(e)和相对风暴径向速度剖面图(f)(剖面由雷达站沿径向指向远离雷达侧)Fig.1 The reflectivity factor(a),raw radial velocity(b),processed relative storm radial velocity graph(c),corresponding reflectivity factor profile(d),radial velocity profile(e),and relative storm radial velocity profile(f) along the black lines based on Leshan Radar at 3.4° elevation angle at 2334 BT 6 Aug 2016(the profile is directed away from the radar side by the radar station in the radial direction)

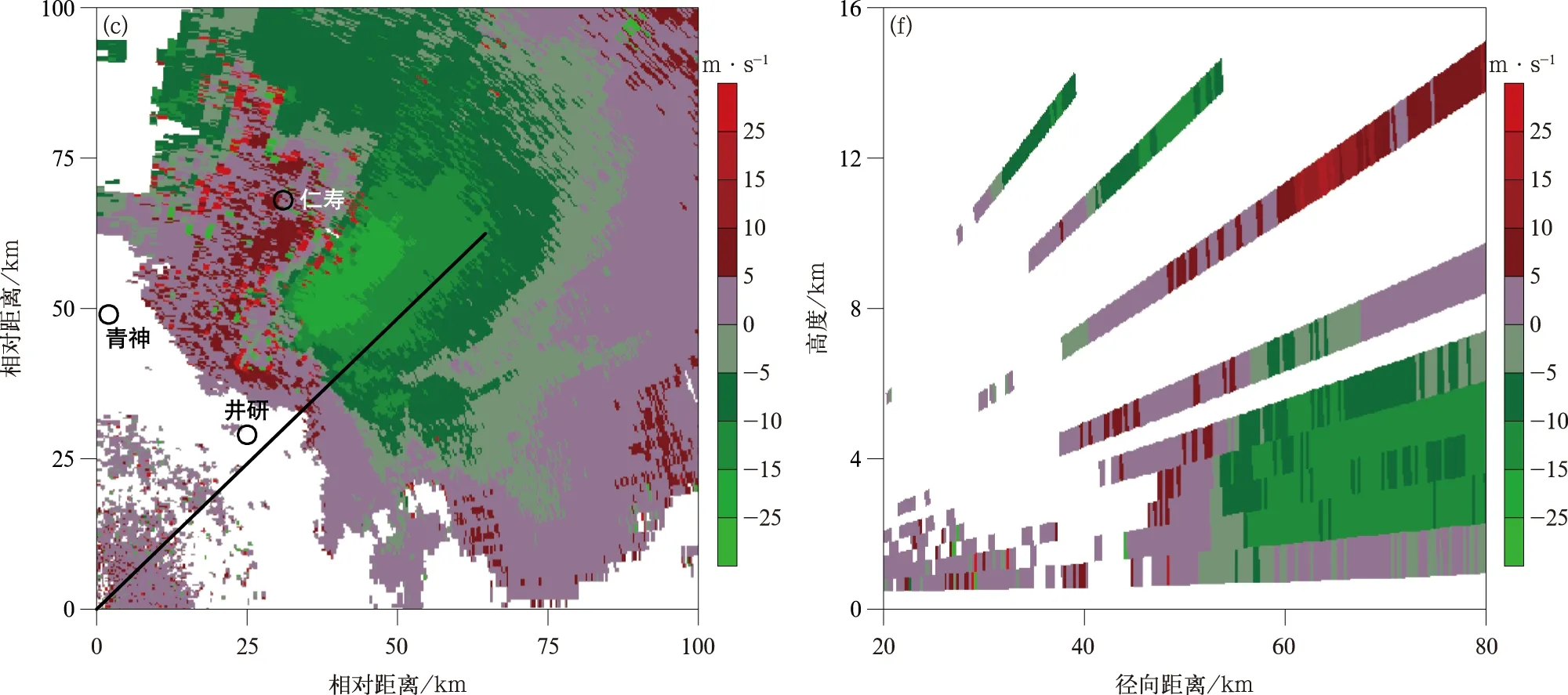
续图1

图2a为模式模拟的此次过程的反射率因子和中层风场叠加图。模拟回波的形状、强度以及位置均与实况(图略)较吻合，且同样沿着中层环境风向移动。另外对流系统的中层后部入流急流特征(图2b)以及地面大风特征(图略)均可模拟再现，因此本文假设模式输出的风暴结构风场与实际风场一致。图2b为沿图2a飑线移动方向(图2a中红色直线)的垂直剖面图。其中风矢量场表示水平风场与垂直运动合成，其中水平风场为沿剖面线的u，v合成风减去飑线移速后的相对飑线水平风场。图2b显示，飑线前侧近地层相对风暴的暖湿入流气流受飑线后侧下沉冷气流强迫抬升后，在对流层中层与飑线后侧入流急流引导的干冷气流相遇形成风向相反的辐合流场，该辐合流场较真实反映风暴内部本身的气流结构特征。后侧干冷气流入侵风暴体后将促使风暴中降水粒子强烈蒸发冷却形成冷池，同时后侧入流与前侧入流汇合后，在风暴体后侧下沉至地面从而引导中高层动量下传，产生地面大风，这是MARC特征可预警雷暴大风的主要依据。假设飑线移向与雷达径向方向一致时，该辐合流场在雷达径向速度场上将表现为典型的“正-负速度区域对”。此时，利用基于搜索“正-负速度区域对”的自动识别算法可识别出MARC特征，该算法在相对风暴风场基础上对径向辐合特征进行识别，因此称为SRMARC特征自动识别算法。

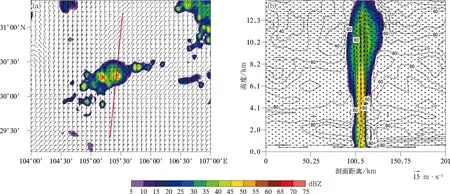
图2 模拟的2016年8月7日01:00四川盆地飑线最大反射率因子(填色)以及中层环境风场(风羽，单位:m·s-1)(a),沿图2a红色直线的垂直剖面图(其中阴影为反射率因子，箭头为风矢量(风速矢量的垂直分量表示垂直速度的2.0倍)，等值线为相对湿度(单位:%))(b)Fig.2 Simulated maximum reflectance factor(the shaded) and mid-level environmental wind field(the barb,unit:m·s-1) of the squall line at 0100 BT 7 Aug 2016(a),vertical section along the red line in Fig.2a(where the shaded is the reflectivity factor,the arrow is the wind vector(the vertical component of the wind speed vector represents 2.0 times of vertical velocity),the contour is relative humidity(unit:%))(b)

U·p-V·p=U*-V·p。

(1)

由于在30～150 km径向距离范围内，风暴回波所在的最高仰角为6°左右，投影系数p约等于1。因此，相对风暴的径向速度可由径向速度直接减去风暴移速得到。在相对风暴的径向速度场中，风暴前侧低层的入流气流与中层后部入流气流的径向方向相反，从而在雷达径向图像上易形成典型的“正-负速度区域对”MARC特征，此时可利用搜索正-负速度段的方法进行MARC特征自动识别。上述分析基于模拟的风暴单体，且在假设风暴移向与风暴所在雷达径向一致情况下得到。图1中该飑线实际移向与风暴主体所在雷达径向方向(即剖面线)较一致，因此本文将采用类似思路对该实际风暴的回波径向速度场进行处理，并构建算法。

飑线系统由多个雷暴单体紧密组织而成，若要区分和识别其中某个风暴单体并获取其移动速度比较困难，获取飑线系统整体移速相对容易，因此本文使用飑线整体移速替代雷暴单体移速。飑线移动速度主要受高空引导气流和前向传播共同影响[11]，飑线整体移速一般较单体更快，因此本文将风暴整层基本径向速度减去飑线整体移速的一定比例值，得到更接近真实的相对风暴单体的径向速度场。另外，大量飑线个例的雷达回波资料分析表明，当飑线处于成熟阶段时，其中层后部常存在RIJ，促使飑线移动速度加快[24]。由于RIJ的速度在对流层中高层随高度增加而减弱(图1e)，当风暴整层基本径向速度直接减去飑线整体平均移速后，在对流层中高层的相对风暴径向速度图上，飑线后侧入流的径向速度(绝对值)较小，范围将减小，此时该区域很可能未被搜索到。由图2b中还可见，风暴在6～9 km高度的相对风暴后部入流气流的风速接近于零，导致搜索后侧入流困难，不利于风暴中高层径向辐合特征的自动识别。因此，为了尽量避免中高层的径向辐合特征被漏识别，需利用飑线整体移速的一定比例值计算相对风暴径向速度场。基于上述分析，本文利用原始径向速度场减去飑线整体移速的三分之二(三分之二是基于多个个例分析后给定的经验值，该参数可调整)得到相对风暴的径向速度图(图1c)及其剖面图(图1f)。由图1f可人工分析出风暴在2～8 km高度范围内存在明显的径向辐合特征，该SRMARC特征为典型“正-负速度区域对”的中层径向辐合特征，可利用搜索正-负速度段的方法识别径向辐合特征。由于径向辐合强度与正-负速度段的速度差有关，径向辐合特征的正-负速度段同时减去风暴移动速度一定比例值后，对计算径向辐合强度值基本无影响，但对辐合的厚度和高度有影响。

3 相对风暴中层径向辐合特征自动识别算法

基于上述典型个例的讨论，本文设计了相对风暴的径向辐合特征自动识别算法。整个算法为4部分，按算法实现流程顺序分为雷达基数据预处理、单径向上正-负速度辐合对的识别、二维径向辐合块识别和三维径向辐合体识别。

3.1 雷达基数据预处理

算法第1步是雷达基数据质量控制(利用模糊逻辑方法剔除杂波)，针对径向辐合处有较多径向速度奇异值(双脉冲重复频率技术造成的)的问题，本文采用肖艳姣等[25]提出的方法进行修正。为了将非典型“正-负速度区域对”变换成典型的“正-负速度区域对”，根据第2章所述，将分析风暴的整体径向速度场减去飑线移动速度(飑线移速和移向通过相关软件采集多个连续体扫中的方位和径向距离计算所得)的三分之二，得到相对风暴的径向速度场，在此基础上搜索典型的“正-负速度区域对”进行SRMARC自动识别。

3.2 识别单径向正-负速度辐合对

本文定义某径向上满足一定条件的正-负速度区域对(或正-负速度段对)为“单径向正-负速度辐合对”(简称径向辐合对)。图3为径向辐合对示意图，正速度段位于雷达站与负速度段之间，其中径向速度值为等距离抽取图1c中剖面线所在径向上有效范围内的径向速度整数值。

图3 径向辐合对示意图(方格内数值为等距离抽取图1c中剖面线所在径向上有效范围内的径向速度整数值，单位：m·s-1，开始和结束的径向距离分别为51 km和61 km)Fig.3 Schematic diagram of radial convergence pair(the values are the integral values of radial velocity(unit:m·s-1) in the radial direction of the section line in Fig.1c,and the radial distances at the beginning and the end are 51 km and 61 km，respectively)

算法第2步(算法流程见图4)主要功能为径向辐合对识别，该模块是整个算法的核心。在上述限定区域内的逐个扫描层(scanning layer，Sli，i=1,2,…,7)，分别从360个方位角(azimuth，Azj，j=1,2,…,360)的径向上搜索正-负速度段，然后对其进行配对并计算其辐合特征参数。首先从有效范围内距离雷达最近的距离库(rang bin，RBk,k=1,2，…，988)开始搜索，即第1个距离库(RBk，k=1)，当径向速度(radial velocity，V)绝对值大于等于0.5 m·s-1且高度在2.5～8 km范围内时，将该值(包括仰角、方位、距离、高度等相关参数信息)放入临时径向速度段列表(temporary radial velocity list，TVL)中，接着判断下一个距离库的径向速度值与TVL的第1个值是否同号。若同号，且该距离库与之前刚放入TVL的距离库值之间的径向距离小于4 km(由于四川的SC型雷达径向速度产品质量较差，有较多奇异值，为了减小奇异值的影响，增大该阈值，该阈值可根据实际情况调整)，同时TVL的径向长度(段首值与段末值的径向距离差)小于20 km (飑线对流系统的一般宽度，该阈值可调整)，则将该值放入TVL中；如果TVL的径向长度大于20 km，且TVL中径向速度数量大于6时(若小于6舍弃掉该TVL，即舍弃一些特小尺度的径向辐合特征)，将TVL的信息赋值给径向速度段，并给该径向速度段配上段号(分为正和负速度段，均从1开始编号)，段号随之增加1，清空TVL并装入该RB的信息，此流程称为“装箱”。若异号，或该RB与之前刚放入TVL的距离库值之间的径向距离大于4 km时，均执行“装箱”流程。当遍历到该径向上最后一个有效值(valid bin number，VBN)时，则将TVL的信息赋值给径向速度段，并给该径向速度段配上段号，最后清空TVL。此时，第1根径向上速度段的搜索工作完成，接着将提取到的径向正-负速度段进行配对。先从段号均为1的正-负径向速度段开始对某径向上所有的正-负速度段进行遍历，选出满足如下条件的正-负速度段对进行配对。

图4 正-负速度辐合对识别算法流程图Fig.4 Identification algorithm of positive-negative velocity convergence pair flowchart

首先，正速度段要位于负速度段与雷达站之间，即正速度段最后一个距离库值的径向距离要小于负速度段最开始一个值的径向距离(图3)。其次，正-负速度段中心值(即段内最大绝对值)距离(如图3)需小于12 km[21]。当正-负速度段配对成功后，计算该速度段对的径向辐合强度。正-负速度区域对径向辐合强度的计算，一般采用正-负速度段中心值差的绝对值除以中心值之间的距离所得。但一个速度段上的径向速度值(绝对值)在径向上并非线性分布，中心值(也有可能是奇异值)的位置往往不在大值区域的几何中间位置，这将导致计算径向辐合强度的不确定性较大。因此，本文定义径向辐合强度为正速度段与负速度段的平均值(绝对值)之和除以两个速度段的平均值距离(从辐合处开始，在负速度段上远离雷达方向最先小于负速度段平均值的距离库径向距离，减去正速度段上朝向雷达方向最先大于正速度段平均值的距离库径向距离，见图3)。该计算结果与实际值相比有偏差，但可避免计算的强度值出现奇异值和大幅波动，同时也能表征径向辐合的强弱。计算径向辐合强度用于判断地面大风的强度，若计算标准一致即可区分其强弱。图3中正速度段的平均值约为2.7 m·s-1，负速度段的平均值约为-10 m·s-1，径向辐合对的平均径向距离约为4 km，因此该径向辐合对的径向辐合强度值约为3.1 s-1。若用正-负速度段中心值差的绝对值除以中心值距离(正-负速度段内最大绝对值所在径向距离之差，见图3)计算径向辐合强度约为2.9 s-1，两种算法所得结果相差较小。另外，统计分析多个类似样本数据的两种计算结果，两者差值均在1 s-1以下，可见该强度计算方法可靠。

为了剔除辐合不明显的速度对，本文设计当正-负速度段平均速度值的绝对值之和大于6 m·s-1且其径向速度中心值的绝对值之和大于12 m·s-1时，才计算其径向辐合强度等参数，否则，舍弃该径向辐合对。当计算的径向辐合强度大于等于1 s-1，再计算该正-负速度段对的方位、径向距离、高度等参数，并将这些信息装入径向辐合实例列表。

3.3 识别二维径向辐合块和三维径向辐合体

算法第3步将各扫描层内所有的径向辐合对进行遍历，找出满足一定条件的径向辐合对并拼连成二维径向辐合块。相当于对径向辐合对求水平相关，以第1个径向辐合对为基础，按径向方位角从小到大依次判断两个径向辐合对的方位角是否小于等于3°，且径向距离(某个辐合块内所有距离库值的径向距离的平均值)之差是否小于等于6 km。若满足该条件就将其装入上一个径向辐合块里，若不满足则将其装入另一个径向辐合块，继续判断下个方位角的辐合对。当某扫描层内的径向辐合对均遍历完后，再判断每个辐合块里辐合对的数量，若数量大于等于3(小于3则舍弃，即舍弃掉小尺度的径向辐合区)，计算辐合块的平均径向辐合强度，并判断该辐合块内所有辐合对的强度值是否小于平均值的3倍。若大于3倍则视为奇异值，将其丢弃，并重新计算辐合块的平均径向辐合强度，再重复上述流程直至所有辐合对强度值均小于3倍平均值。然后将辐合块的平均径向辐合强度、最大径向辐合强度、方位、径向距离、高度等信息，一并装入辐合块列表中。

算法第4步将每层的径向辐合块做垂直相关分析，求得三维风暴径向辐合体。每个确定的三维风暴辐合体由一个或多个在相继仰角上的二维径向辐合块构成。首先，将最低层的第1个径向辐合块放入临时径向辐合体中，然后遍历剩下的所有径向辐合块，当某个径向辐合块与第1个辐合块的层次不同、方位角差小于等于6°且径向距离小于等于8 km 时，将其放入临时径向辐合体。若不满足上述条件，将该辐合块放入存储剩余径向辐合块的列表里。遍历完所有径向辐合块后，将临时辐合体赋值到第1个径向辐合体并编号，清空临时辐合体，再计算该辐合体的平均径向辐合强度、最大径向辐合强度、径向辐合厚度、径向辐合中心高度等参数。当剩余径向辐合列表中的径向辐合块个数大于等于1时，重复上述三维相关分析流程，直至临时径向辐合体中辐合块个数为零，整个算法结束。

4 算法测试

4.1 个例分析

本文使用2013年8月18日(简称“8·18”)和2018年8月7日(简称“8·7”)发生在四川盆地的两次飑线天气个例的雷达体扫资料对该算法进行测试，并对算法在原始径向速度场(raw radial velocity，RRV)和相对风暴径向速度场(relative storm radial velocity，RSRV)上识别出的径向辐合特征结果进行对比分析。

两次过程均受东风波系统影响产生，造成大风、短时强降水等灾害性天气。图5为这两次过程的反射率因子和径向速度图，飑线回波主体均朝着雷达站方向移动。“8·18”过程的反射率因子图呈现弓形(图5a)，弓形回波主体南段在径向速度图上均表现为非典型“正-负速度区域对”径向辐合特征(图5b)。“8·7”过程的反射率因子图呈现线状(图5c),回波主体两侧在径向速度图上均表现为非典型“正-负速度区域对”径向辐合特征(图5d)。接近两次过程发生时的探空图(图略)均表明，从对流层低层至中高层风向较一致，有利于径向速度图上呈现非典型“正-负速度区域对”径向辐合特征。图5中实线是在RRV上利用搜索雷达某径向上的“正-负速度区域对”方法识别出的径向辐合块，虚线是利用相同方法在RSRV上识别出的径向辐合块。

图5a和图5b分别为“8·18”过程由宜宾雷达观测到的2.4°仰角上的反射率因子和(原始)径向速度，其中标注的A,B,C代表该算法识别出的3个径向辐合块。其中辐合块B(高度约4.9 km)，在RRV和RSRV(RRV加上飑线移速15 m·s-1的三分之二，即RRV加10 m·s-1)中均被识别。但RRV中算法只识别出B的北段，其呈现出典型“正-负速度区域对”的径向辐合特征；RSRV中算法不仅识别出B的北段，还识别出其南段的非典型“正-负速度区域对”的径向辐合特征。由于径向辐合块C的负速度段速度较小，该负速度段加10 m·s-1后，在RSRV上将无法搜索到负速度段，因此在RSRV中算法未识别出来。从图5b上可看出，辐合块C的径向辐合强度较弱，由于弱径向辐合特征识别意义不大，且这种情况只在个案中存在，非普遍现象，因此不影响该算法的整体效果。另外，算法在RSRV上识别出径向辐合块A，但在RRV上未能识别出。图5c和图5d分别为“8.7”过程由南充雷达观测到的4.3°仰角上的反射率因子和(原始)径向速度，图中标注的E、F、G代表该算法在RRV上识别出的3个径向辐合块(实线)，它们在RRV和RSRV(RRV加上飑线移速9 m·s-1的三分之二，即RRV加6 m·s-1)中均被识别。但RRV中算法未识别出F和G之间的辐合块以及E东侧的辐合块，其为非典型“正-负速度区域对”；RSRV中算法识别出整段径向辐合块，包括其两侧的非典型“正-负速度区域对”径向辐合特征。上述分析表明，在RSRV上利用搜索“正-负速度区域对”方法识别径向辐合特征的效果更好。

图5 2013年8月18日00:49宜宾雷达2.4°仰角反射率因子(a)、原始径向速度(b)以及 2018年8月7日20:15南充雷达4.3°仰角反射率因子(c)、原始径向速度(d)(实线和虚线分别表示原始和相对风暴径向速度场上识别出的径向辐合块，标注A，B，C，E，F，G分别代表算法识别出的径向辐合块)Fig.5 The reflectivity factor(a) and raw radial velocity(b) based on Yibin radar station at 2.4° elevation angle at 0049 BT 18 Aug 2013 and the reflectivity factor(c) and original radial velocity(d) based on Nanchong radar station at 4.3° elevation angle at 2015 BT 7 Aug 7 2018(the solid line and the dashed line respectively represent the radial convergent blocks identified in the RRV and RSRV, and the labels A,B,C,E,F and G represent the radial convergent blocks identified by the algorithm)

4.2 识别评分

为了更全面地检验算法对中层径向辐合特征的识别能力，选取2009—2018年10次飑线雷暴大风天气过程(表1)进行测试。由于只有当强对流系统的移动方向与系统所在雷达径向方向之间夹角较小时，径向速度图上才会呈现较为明显的中层径向辐合特征，所以挑选的10次过程均满足该条件。表1中一个样本即为一个体扫，其中测试样本量为经人工剖切分析后确认有明显MARC特征的体扫个数；另外当算法自动识别出某个体扫的MARC与人工确认的较一致时(漏、空识别的MARC数量小于等于2)，该体扫即为算法成功识别的样本。由表1可见，该算法能有效识别出的样本数量达到47个，识别准确率达到82.4%。具有非典型“正-负速度区域对”的中层径向辐合特征的测试样本数量为25，算法程序能正确识别出21个，表明算法对非典型MARC特征有较高的识别水平。将算法程序搜索出的正-负速度段与对应的径向速度图进行人工对比分析发现，算法未能识别出的主要原因是由于径向速度段的平均值较小，不能满足算法程序设置的参数阈值，被舍弃。因此，还需要对更多个例进行测试，不断优化算法各参数阈值，才能使识别算法达到最佳状态。

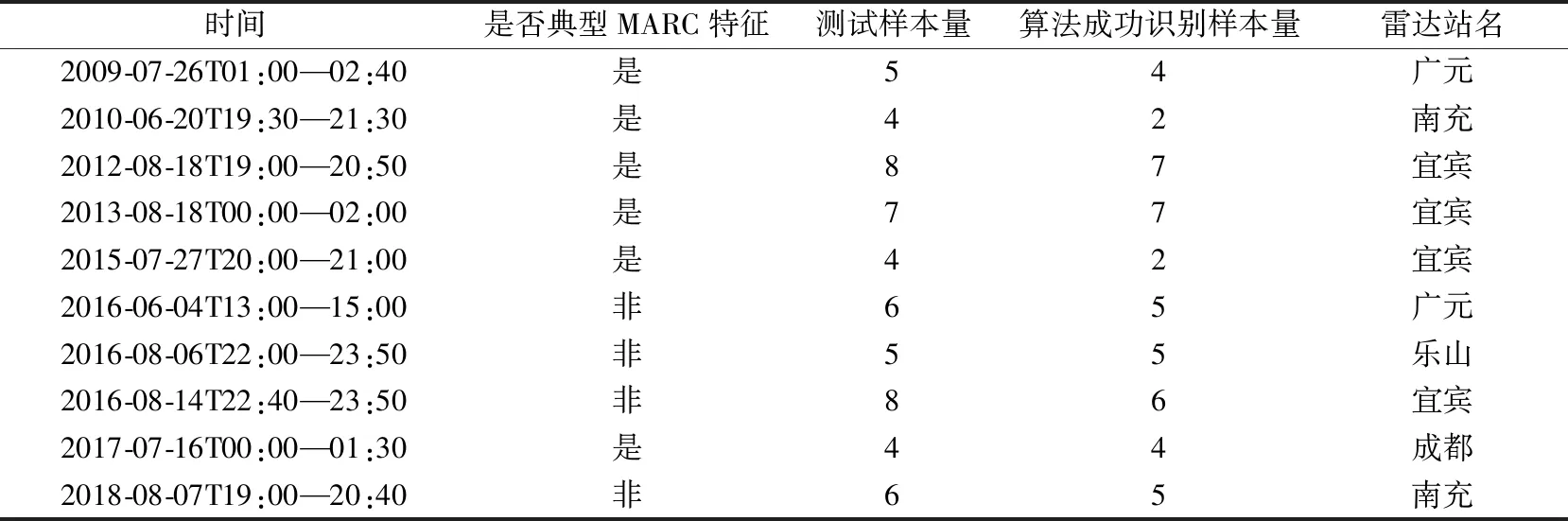
表1 检验识别算法的飑线个例及识别结果Table 1 Examples of squall line to test the recognition algorithm and recognition result

5 算法应用

利用上述SRMARC特征自动识别算法，对第4章评分检验所选部分个例进行特征识别并计算其特征参数。特征参数包括平均径向辐合强度(average radial convergence strength，ARCS)、最大径向辐合强度(max radial convergence strength，MRCS)、径向辐合体厚度(radial convergence thickness，RCT)、径向辐合体中心高度(radial convergence height，RCH)。本文定义ARCS指辐合体各层径向辐合块平均强度值之和除以辐合体层数所得，单位为s-1；MRCS指辐合体内所有径向辐合块最大强度值中的最大值，单位为s-1；RCT指辐合体最高层径向辐合块高度减去最低层径向辐合块高度所得，单位为 km，当辐合体只有一层时，辐合块高度设为1 km；RCH指辐合体内所有径向辐合块高度之和除以层数所得，单位为km。当识别的某个径向辐合体前侧10 km径向距离范围内有站点的极大风速记录值为过程最大值时，且飑线影响该站点之前6 h内，站点周围无对流系统影响，将该风速值与对应的辐合体特征参数作为一组样本。本文利用SPSS软件对采集的样本数据(共71组样本)进行统计分析，分析结果如图6所示。由图6可以看到，ARCS,MRCS,RCT与地面极大风速之间有较好的线性相关性，且均为正相关，其中ARCS与地面极大风速相关系数最大(r为0.79)，MRCS次之(r为0.67)，RCT相关性最差(r为0.5)，但均达到0.01显著性水平。表明飑线内径向辐合特征越明显，对应地面大风越强。强大风(大于20 m·s-1)样本中大部分样本的ARCS超过3 s-1，MRCS超过4.5 s-1，RCT高于2.5 km。弱大风(小于20 m·s-1)样本中大部分样本的ARCS低于4 s-1，MRCS低于8 s-1，RCT低于3.5 km。因此，根据径向辐合特征的这些参数值可大致判别地面大风的强度，为对流性大风的监测预警和灾害评估提供参考依据。

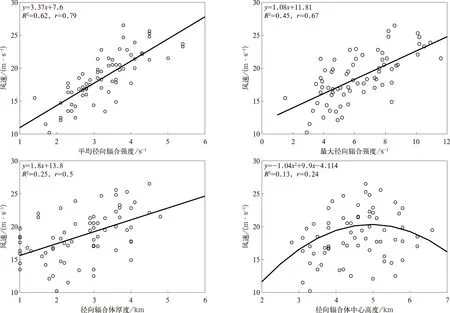
图6 地面极大风速与相对风暴径向辐合特征参数散点分布及拟合曲线Fig.6 Scattered point distribution and fitting curve of the ground maximum wind speed and relative storm radial convergence characteristic parameters

对线性相关性较强的3种特征样本进行线性拟合，拟合线性方程如图6所示，由图6可以看到，ARCS的拟合效果最好(决定系数R2为0.62)，MRCS次之(决定系数R2为0.45)，RCT最差(决定系数R2为0.25)。另外，径向辐合体中心高度参数的二次曲线模型拟合在各种模型中效果最佳，决定系数R2为0.13，拟合优度较低。但从其散点分布看，径向辐合体中心高度越高并不意味着地面大风越强，中心高度值在3.5～6.0 km高度，地面容易出现强大风(大于20 m·s-1)。这是由于飑线系统发展初期，回波质心较高，对流风暴内以上升气流为主，下沉气流较弱。

通过分析“8.18”过程雷达回波及地面大风强度演变发现，算法首次识别出SRMARC特征(ARCS超过1 s-1)的时间为2013年8月18日21:13，地面观测极大风速首次达到17.1 m·s-1以上的时间为21:47，极大风速首次达到20.0 m·s-1以上的时间为22:12，通过算法识别的径向辐合特征可以提前约30 min预警此次大风。算法首次识别出2016年8月6日盆地飑线过程SRMARC特征(ARCS超过1 s-1)的时间为22:21，地面首次出现大于17.1 m·s-1极大风速的时间为22:55，算法识别可以提前约35 min预警此次大风。其他多次飑线过程也均可提前20～30 min 预警地面大风，这与Schmocker等[16]以及吴翠红等[17]的研究结论较一致。

6 结论与讨论

研究表明：

1) 本文提出相对风暴中层径向辐合特征自动识别算法。该算法首先搜索出单仰角相对风暴径向速度图上每个径向上的正-负速度段，并按照规则对其进行配对，形成径向辐合对，对不明显的径向辐合对进行消空处理。然后在二维锥面上对径向辐合对做水平相关分析得到二维径向辐合块。最后当所有仰角遍历完后，对二维辐合块做垂直相关分析得到风暴的三维径向辐合体，并计算出三维辐合体的强度、厚度、中心高度等重要特征参数。

2) 利用两次具有非典型“正-负速度区域对”径向辐合特征的飑线雷达资料对该算法进行测试，结果表明：在RSRV上通过搜索正-负速度段识别径向辐合特征的效果较原始径向速度场上更好。中小尺度天气系统运动场主要通过旋转运动和平移运动及上升运动构成。基本径向速度场是旋转运动和平移运动综合影响的结果，当平移运动速度大于旋转运动速度时，系统在基本径向速度场上的切变(旋转、辐合或辐散)特征可能被掩盖。这是利用相对风暴径向速度识别系统中层辐合的优势所在。利用该算法对10次雷暴大风强对流天气过程的中层径向辐合特征进行识别测试结果表明，该算法识别准确率达到82.4%，并且对非典型MARC特征有较高的识别水平。

3) 径向辐合特征参数中ARCS，MRCS，RCT与地面极大风速之间有较好的线性相关性，且均为正相关，其中ARCS与地面极大风速相关系数最大，MRCS次之，RCT相关性最差，但均达到0.01显著性水平。表明飑线的径向辐合特征越明显，对应地面大风越强。通过算法识别的径向辐合特征可以提前约30 min预警此次大风。

由于本文的SRMARC特征自动识别算法是基于大量飑线型强对流天气个例的雷达资料获得，该算法是否适用于非飑线类型对流系统尚需分析和检验。值得一提的是文中所涉及的飑线移动方向和速度是通过其他软件获取，需将SCIT算法嵌入后才能全面实现自动化识别。另外，本文拟合的特征参数与大风风速之间的相关关系(方程)，是基于四川个例资料所建，应用于其他地区适用性有待探讨。该算法还可以扩展至下击暴流天气系统的低仰角径向速度辐散特征、冰雹天气系统的高层径向辐散特征以及短时强降水天气系统的低层辐合特征的自动识别，具有一定应用前景。