考虑多主体主从博弈的多微网协调优化调度
2021-01-29练小林李晓露黄海峰
练小林,李晓露,曹 阳,张 鸿,黄海峰
(1.上海电力大学电气工程学院,上海 200090;2.中国电力科学研究院有限公司,南京 210003)
为了应对传统能源枯竭、环境污染及气候变化带来的严峻挑战,可再生能源得到迅速发展。微网作为一种容纳分布式能源的重要组织形式,对电力系统安全运行有着重要作用[1]。随着分布式能源渗透率的不断提高,局部配电区域内将存在多个微网。多微网之间通过电能交互能够有效促进分布式能源就地消纳,提高系统运行稳定性[2]。
售电侧电力体制改革的不断推进使得拥有分布式能源的微网可以根据自身利益需求参与电能交易[3]。然而由于各微网属于不同的利益主体,故不同微网的利益诉求不同。因此,如何在兼顾各方主体利益的前提下实现多微网协调运行是亟需解决的重要问题。
目前,众多文献已证明博弈论能够有效解决多利益主体间的策略优化问题[4-5]。在与多微网协调优化相关的博弈方面,文献[6]建立了配网和多微网之间的Stackelberg博弈模型,通过电价激励增强微网间的电能交互。文献[7]提出了基于合作博弈论的光伏微网群电能交易模型,降低了系统运行成本。然而,以上研究均忽视了微网的二重性,尚未从“源”、“荷”两个角度出发,对多微网优化调度进行深入研究。
在充分考虑微网二重性的情况下,文献[8-10]提出了基于双向拍卖机制的多微网能量优化模型,通过双向拍卖交易机制解决买卖双方交易过程中的规则、秩序问题。文献[11]通过采用合作博弈论及引入报价矩阵建立了买卖双方多主体参与电能交易的竞价机制,但未对多个买方及多个卖方之间的博弈问题进行研究。文献[12]提出了基于多智能体的多微网电能交易策略,通过采用非合作博弈确定卖方的最优售电方案,但未考虑买方之间的博弈行为。文献[13]充分考虑多主体间的博弈问题,提出了基于主从博弈的多微网电能交易模型,但仅适用于多微网供需平衡的情况,未考虑买卖双方需求不等的情况。
针对以上问题,本文提出考虑多主体主从博弈的多微网协调优化模型。日前调度阶段以微网运行成本最低为目标优化储能充放电功率;实时调度阶段通过建立多主体主从博弈模型研究多微网间电能交互问题。其创新性在于:①充分考虑微网二重性,建立了发电微网、用户微网的多主多从博弈模型,并证明了该模型均衡解的存在性;②通过非合作博弈模拟发电微网之间价格竞争的同时,采用演化博弈求解多微网间电力消费行为策略;③采用二次效用函数描述微网的需求侧满意度大小,并分析其对多微网协调优化产生的影响。
1 多微网两阶段协调优化模型
综合考虑可再生能源出力和负荷需求的波动性,本文的优化阶段包括日前阶段和实时阶段。日前优化阶段,根据可再生能源和负荷的日前预测数据,以微网运行成本最低为目标,优化储能充放电功率;实时优化阶段,基于储能日前充放电计划及可再生能源出力和负荷功率波动,通过构建多主体主从博弈模型,实时协调优化微网间的交互电能。
1.1 日前调度模型
1.1.1 目标函数
微网的运行成本主要包括储能系统运行成本、负荷调度补偿成本、微网间电能交易成本以及微网与配电网之间的电能交易成本,故日前调度的目标函数为
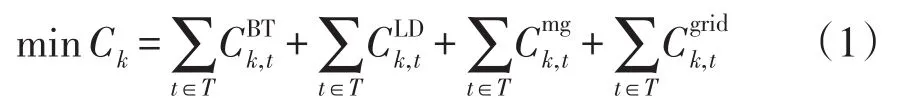
各成本的具体表达式如下:
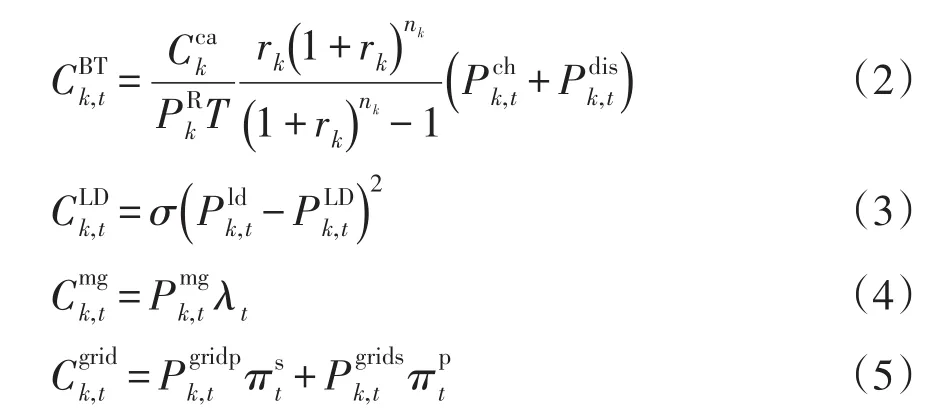
1.1.2 约束条件
1)功率平衡约束
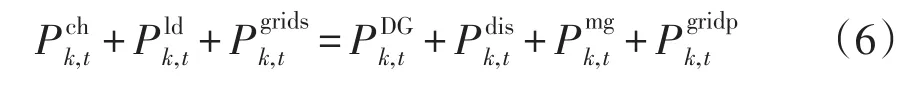
2)储能电池运行约束
储能电池的寿命与充放电深度密切相关,过充和过放都将加快电池的老化速度,故储能系统应满足以下约束。
储能充放电功率约束为

此外,在同一时段,储能系统不能即充电又放电,故还应满足储能充电功率和放电功率两者乘积为零这一约束条件。
储能容量约束为

式中:Ek,t为t时段微网k储能电池的电量;为微网k储能系统的额定容量;为微网k储能电池荷电状态的最小值;分别为t时段微网k储能的充、放电效率。
3)微网间交互功率约束

4)微网与配电网间交互功率约束

类似地,微网与配电网之间的交互功率也应满足购电功率与售电功率两者乘积为零这一约束。
1.2 实时多主体主从博弈模型
1.2.1 多主体主从博弈结构
实时调度阶段,根据供需比系数SDR(supply-todemand ratio)[14],将微网分为发电微网和用户微网。

当SDRk,t<1时,定义t时段的微网k为用户微网,其集合用I表示;当SDRk,t>1时,定义t时段的微网k为发电微网,其集合用J表示。
为了协调微网间电能交互,本文将发电微网与用户微网之间的策略互动视为Stackelberg博弈过程,主方为发电微网,从方为用户微网。博弈关系包括以下三种:①发电微网和用户微网之间的Stackelberg主从博弈。发电微网以自身经济最优发布电能价格,用户微网根据价格信息做出最优选择,并反馈给发电微网;②发电微网之间的非合作博弈。发电微网根据用户微网的行为策略展开价格竞争,最终达到均衡状态;③用户微网的演化博弈。用户微网之间通过演化博弈模拟行为演化。多主体主从博弈结构如图1所示。
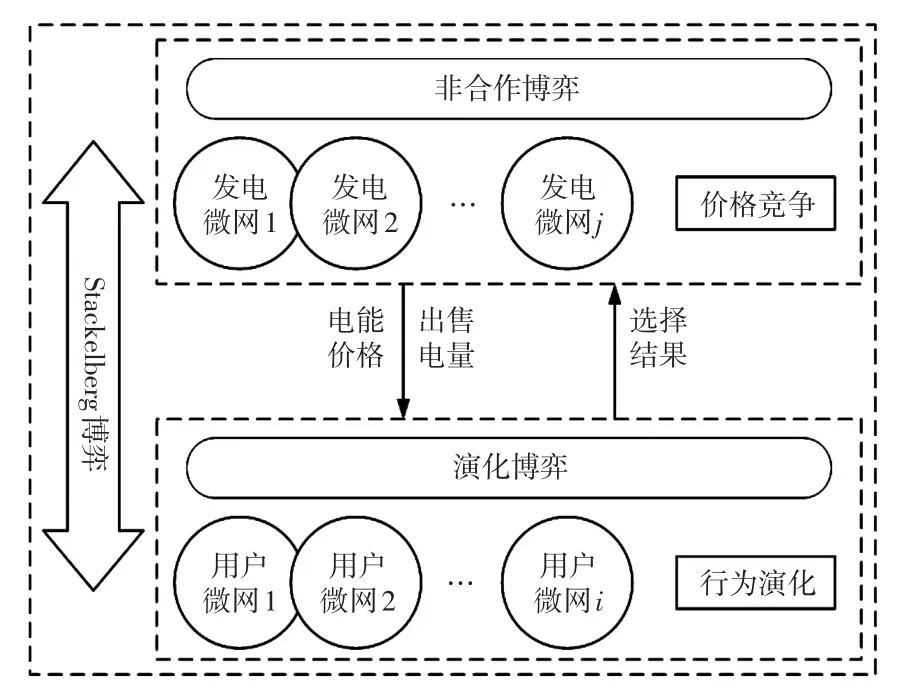
图1 多主体主从博弈结构Fig.1 Multi-agent leader-follower game structure
1.2.2 微网效用函数
由于微网在各时段的供需特性不同,因此对于相同电价,其用电行为也不同。为了描述其用电行为偏好可以采用效用函数。此类效用函数主要包括对数效用函数和二次效用函数两种[15]。由于此类函数关于用电量具有单调不减的特征,从而保证其具有线性边际收益,可表示每个微网用电所带来的满意度大小。本文采用二次效用函数来描述微网需求侧满意度大小。
(1)用户微网的效用函数。用户微网由于电能供应量无法满足负荷需求,需要购买电能以满足供需平衡,其效用函数为
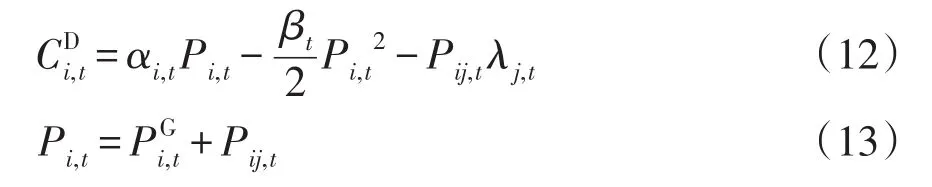
式中:αi,t为t时段用户微网i的需求侧满意度系数;Pi,t为t时段用户微网i实时优化后的负荷需求量;Pij,t为t时段用户微网i与发电微网j之间的交易电量;βt为大于零的常数;λj,t为t时段发电微网j发布的电能价格。
用户微网购买电能时存在以下约束:
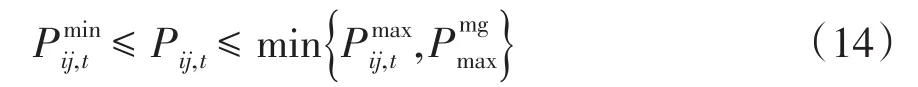
(2)发电微网的效用函数。发电微网通过出售过剩电能以提升经济收益,其效用函数为
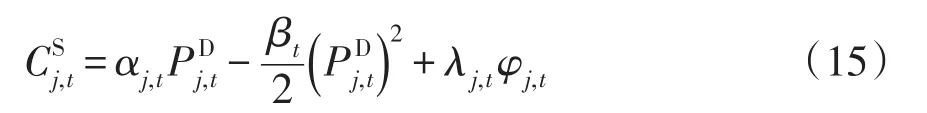
式中:αj,t为t时段发电微网j的需求侧满意度系数;为t时段发电微网j的实时负荷需求量;Pj,t为t时段发电微网j的过剩电量;Qj,t为t时段用户微网从发电微网j购买的总电量;φj,t为t时段发电微网j的出售电量,φj,t=min( )Pj,t,Qj,t,φj,t应满足以下约束:

1.2.3 多主体主从博弈均衡解的存在性
1)用户微网的演化博弈
在演化博弈过程中,每个用户微网根据发电微网发布的电能价格选择一个发电微网购买电能,同时通过不断学习和进化,根据历史经验来调整自身策略。经过一段时间,所有用户微网最终会趋于某个稳定策略,从而达到演化均衡。
假设用户微网在时段t选择发电微网j购买电能的概率为ρj,t,且ρj,t满足以下条件:

由式(12)可得,t时段用户微网i的最优购买电量为

由此可得,t时段用户微网需要从发电微网j购买的总电量为

考虑到发电微网j自身的过剩电量可能不足以满足所有用户微网的购电需求,故t时段用户微网i与发电微网j之间的实际电能交易量为
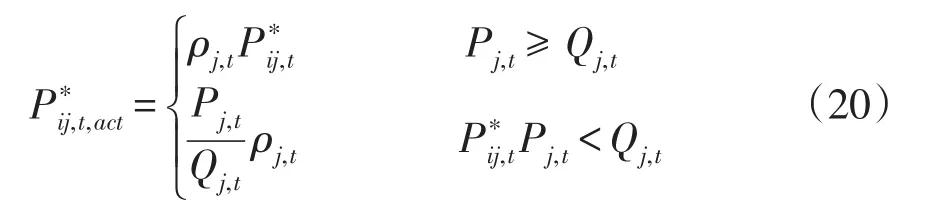
两种情况下,t时段发电微网j可获得的效用ϕj,t可表示为
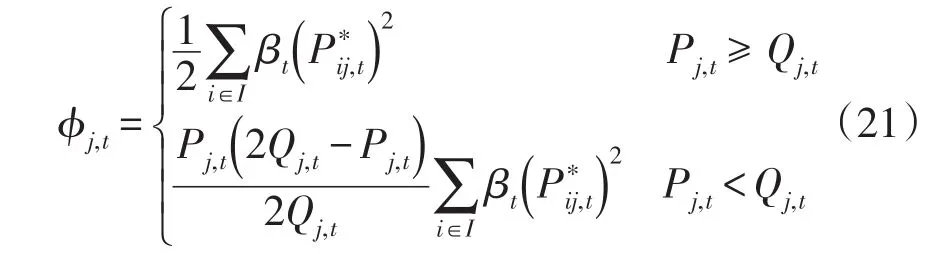
在演化博弈过程中,用户微网基于各策略适应度不断对策略进行选择和进化,故各种策略的概率会发生动态变化。博弈演化的复制动态可描述为


为了获得博弈的演化均衡策略,需求解式(22)的稳定奇点,即

2)发电微网的非合作博弈
为了求解发电微网的非合作博弈模型,需要寻找纳什均衡点。根据纳什均衡点存在性定理:在有限个参与人的博弈问题中,若参与人的策略集合是闭的、有界的凸子集,且策略空间上的每一个效用函数是拟凹和连续的,则该博弈问题存在纳什均衡点。
在发电微网的非合作博弈中,参与人是发电微网,电能价格是发电微网的策略。发电微网的效用函数为
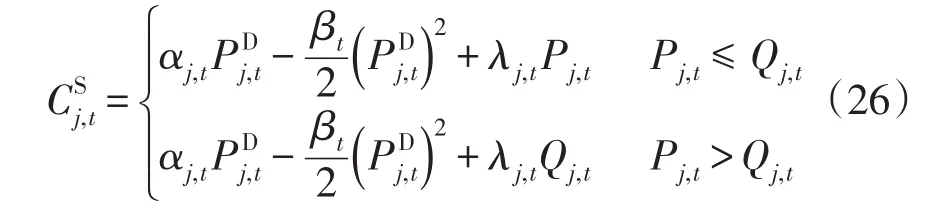
式中,发电微网的个数为j个,即博弈的参与人是有限的。电能价格。因此,j个发电微网的价格策略集合是闭的、有界的凸子集,且当发电微网j参与电能交易时必然有对应的价格策略存在,故策略集合非空。
此外,由式(19)可知,用户微网的总购电需求为

将式(27)代入式(26)可得发电微网的效用函数为
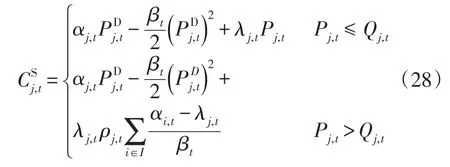

3)发电微网和用户微网之间的Stackelberg博弈
在发电微网和用户微网之间策略互动形成的Stackelberg博弈中,当发电微网通过非合作博弈发布电能价格时,用户微网根据所得价格信息进行动态演化以达到演化均衡。由上述可知,非合作博弈存在均衡解,同时演化博弈的收敛性已得到保证。因此,通过重复上述过程可获得微网间电能交互策略,即Stackelberg博弈存在均衡解。
2 模型求解
2.1 日前调度模型求解
本文选取改进的粒子群优化算法对日前调度模型进行求解。相比于标准粒子群算法,本文选取的改进粒子群算法引入了模拟退火思想。通过利用模拟退火算法在一定概率控制下能够接受一些劣质解的特性,克服标准粒子群算法易陷入局部最优的弊端,改善算法的收敛性能。日前调度模型的求解流程如图2所示,具体步骤如下:
步骤1输入基础数据(可再生能源出力、负荷需求、储能数据等);
步骤2初始化粒子群算法的相关参数(粒子的个数、迭代次数及粒子的速度和位置);
步骤3设置模拟退火的初始温度,计算个体最优解和全局最优解;
步骤4更新粒子的速度和位置,并计算每个粒子的适应度值;
步骤5为粒子随机产生一个新位置,判断新旧 位 置 的 适 应 度 之 差 ΔC。 若 ΔC<0或exp(- ΔC∕T) ΔC>rand(0 ,1),粒子进入新位置;否则根据当前速度和位置计算粒子适应度值;
步骤6更新个体最优解和全局最优解;
步骤7判断是否满足终止条件。若满足条件,则执行步骤8,若不满足条件,则跳到步骤4;
步骤8输出优化结果。
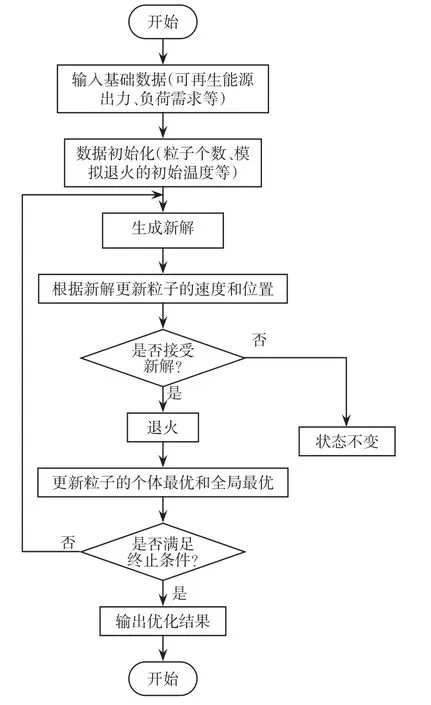
图2 日前调度模型的求解流程Fig.2 Flow chart of day-ahead scheduling model solving
2.2 实时博弈模型求解
在求解实时博弈模型时,用户微网首先根据发电微网发布的电能价格确定最优行为策略,然后发电微网根据用户微网的行为策略调整电能价格,并反馈给用户微网,最终通过多回合博弈求得主从博弈均衡解。求解流程如图3所示。
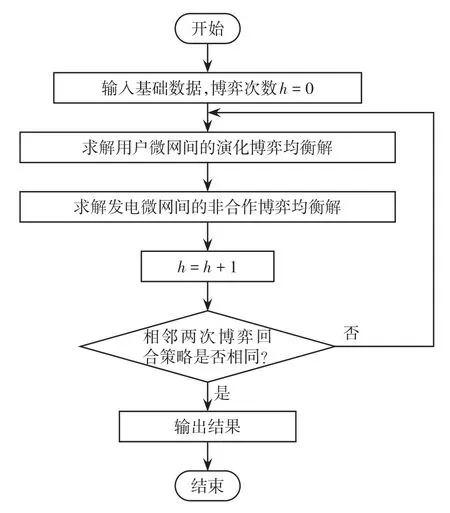
图3 实时博弈模型的求解流程Fig.3 Flow chart of real-time game model solving
其中,发电微网的非合作博弈均衡解求解过程和用户微网的演化博弈均衡解求解过程如下。
(1)初始化电能价格,令非合作博弈迭代次数n=1。
(2)根据演化博弈均衡解,发电微网可获得用户微网的总购电需求。
(3)发电微网根据式(29)计算自身价格更新策略为
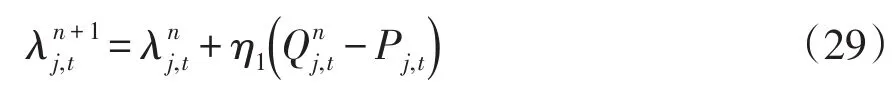
式中,η1为步长因子。
(4)令n=n+1,重复上述步骤,直至满足以下条件。

式中,ε1为允许误差。
用户微网的演化博弈求解过程如下。
(1)数据初始化,令演化博弈迭代次数m=1。
(2)根据发电微网发布的电能价格,每个用户微网选择一个发电微网j购买电能,并计算发电微网j的效用和平均效用值。
(3)根据式(31)更新用户微网的演化行为策略为
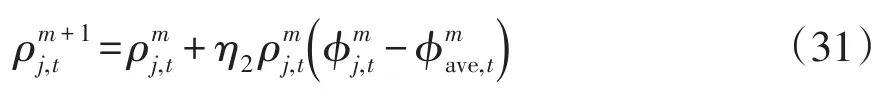
式中,η2为步长因子。
(4)令m=m+1,重复上述步骤,直至满足以下条件。

式中,ε2为允许误差。
3 算例分析
3.1 基础数据
本文选取 5个互联微网(MG1、MG2、MG3、MG4、MG5)进行仿真分析。各微网的可再生能源出力预测曲线如图4所示,实时出力的波动范围为预测出力的90%~110%;负荷需求预测曲线如图5所示,实时需求的波动范围为预测负荷需求的95%~105%。储能系统的额定容量为300 kW·h,最大允许充放电功率为100 kW,充放电效率均为0.9,折旧率取0.005元∕kW2。配电网购售电价如表1,微网间日前交易电价的制定见文献[16]。微网需求侧满意度系数的取值范围为[5,10],β取值0.5。算例调度周期取一天,以1 h为步长将一天分为24个时段选择调度时间段为当日零点至次日零点。
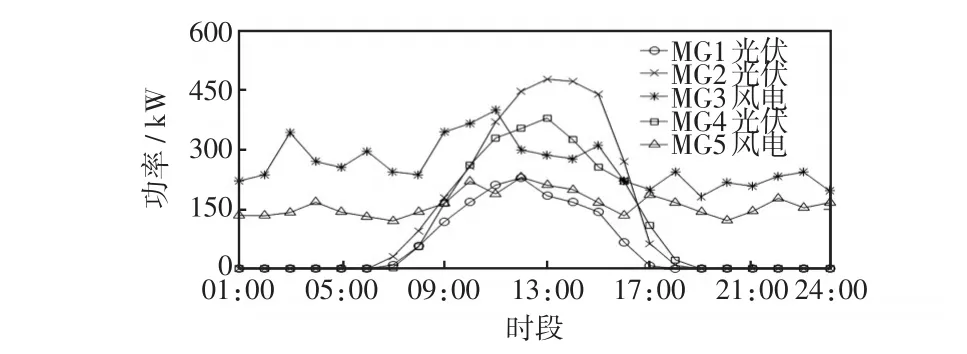
图4 可再生能源出力预测曲线Fig.4 Forecasting curves of renewable energy output
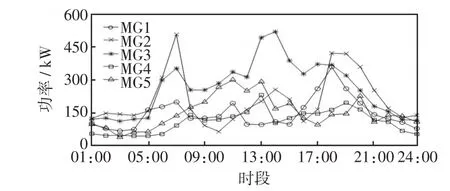
图5 负荷需求预测曲线Fig.5 Forecasting curves of load demand
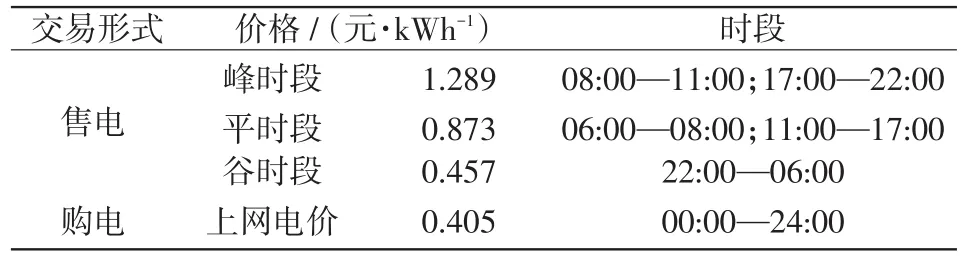
表1 分时电价Tab.1 TOU electricity rates
3.2 优化结果分析
3.2.1 日前优化结果
1)日前储能优化结果
储能的日前充放电功率优化结果如图6所示。

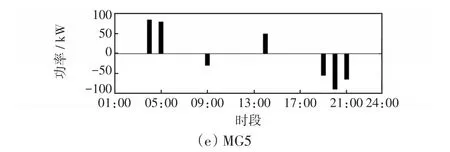
图6 储能日前充放电功率Fig.6 Day-ahead charge and discharge power of energy storage
从图6可以看出,在时段1:00—6:00,各微网的储能系统仅充电不放电,从而将谷电价时段的电能存储起来,满足平时段和峰时段的负荷需求。在时段10:00—17:00,储能通过继续充电来消纳本地过剩可再生能源,以满足晚高峰时段的负荷需求增长。在时段18:00—22:00,MG1、MG2和MG4的储能放电以满足由于可再生能源出力不足造成的电能短缺。MG3和MG5的储能放电功率在满足自身负荷需求的同时,通过将电能出售给其他微网来促进系统供需平衡,提高经济效用。
3.2.2 实时优化结果
实时优化结果将以时段3(MG1、MG2和MG4为用户微网,MG3和MG5为发电微网)为例,从模型收敛性、发电微网的经济效益和可再生能源出力预测偏差的影响三个方面进行分析。
(1)模型收敛性。用户微网购买电能的概率收敛过程和发电微网电能价格的收敛过程如图7与图8所示。用户微网电量需求的收敛过程如图9所示。
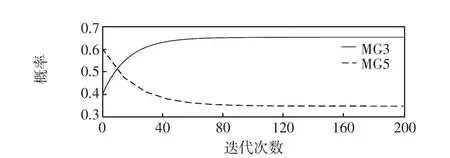
图7 用户微网购买电能的概率收敛过程Fig.7 Probability convergence process of electricity purchased by user-microgrid
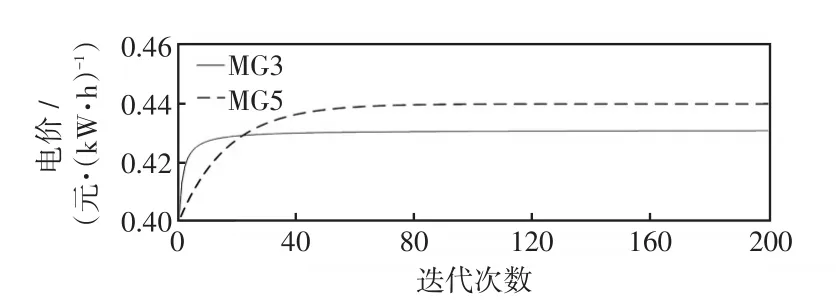
图8 发电微网电能价格的收敛过程Fig.8 Convergence process of generator-microgrid’electricity price
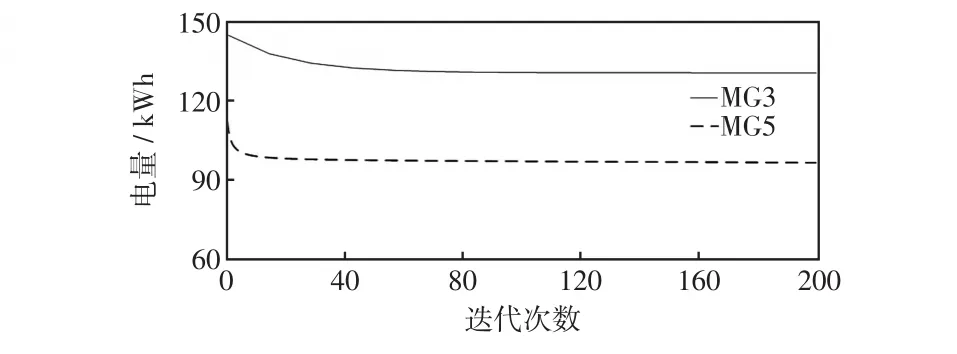
图9 用户微网电量需求的收敛过程Fig.9 Convergence process of user-microgrid’electricity demand
由图7可知,用户微网从发电微网购买电能的概率能够快速收敛到均衡值,即用户微网的动态行为达到演化均衡。由图8可知,发电微网的售电电价最终收敛到了一个固定值,此时发电微网之间的非合作价格竞争达到均衡,与演化均衡一起,构成用户微网和发电微网之间的主从博弈均衡。由此验证了实时博弈模型的收敛性。通过比较图8与图9可以发现,当发电微网的售电电价增加时,用户微网的电量需求呈下降趋势,与微网实际电力消费行为保持一致。
(2)发电微网的经济效益。为了分析发电微网之间进行博弈对其经济效益的影响,将发电微网间无博弈和有博弈两种情况下的经济效益进行了对比,如图10所示。从图中可以看出,相比于发电微网间无博弈的情况,发电微网间有博弈时的经济效益更高。当计及发电微网间的博弈时,发电微网享有议价权,即其电能价格不再是日前售电电价,而是能够根据自身利益对电能价格进行优化,故发电微网间进行博弈对提升系统经济性有着促进作用。
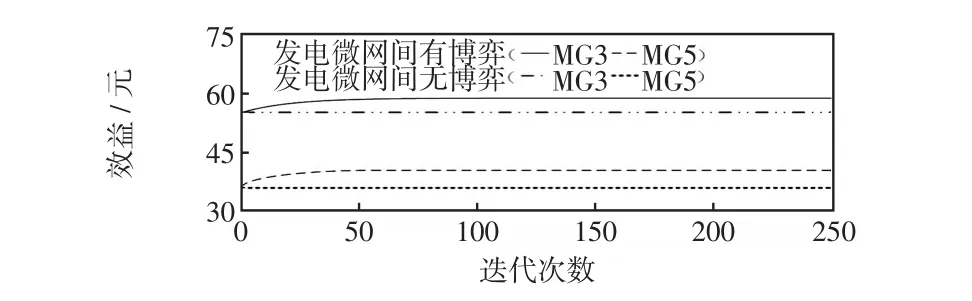
图10 发电微网的经济效益Fig.10 Economic profits of generator-microgrid
(3)可再生能源出力预测偏差的影响。为了探究风光出力预测偏差对主从博弈造成的影响,给出了不同预测偏差下主从博弈的迭代次数,如图11所示。
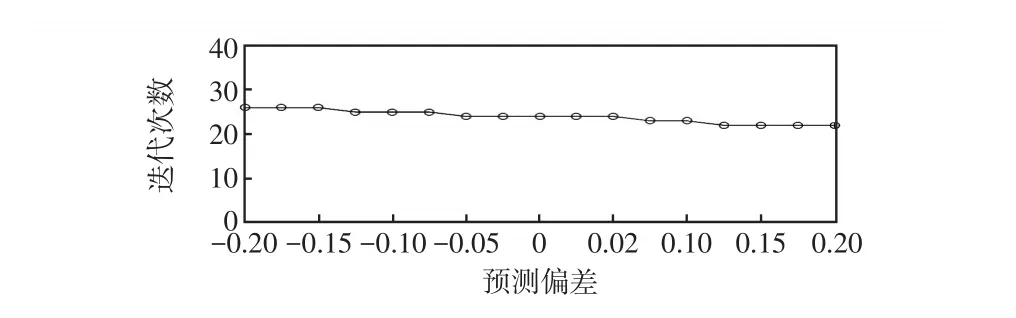
图11 不同预测偏差下主从博弈的迭代次数Fig.11 Iteration numbers of leader-follower game with different prediction deviations
从图11可以看出,风光出力预测偏差与主从博弈迭代次数之间的关系曲线变化非常平缓。当预测偏差为0时,用户微网的总需求电量大于发电微网的总供应电量。在预测偏差从0增大至0.2的过程中,用户微网的总需求电量逐渐减小,发电微网的总供应电量逐渐增大,从而使得两者之间的差值逐渐变小,此时迭代次数略微减小。反之,在预测偏差从0减小至-0.2的过程中,用户微网的总需求电量逐渐增大,发电微网的总供应电量逐渐减小,从而使得两者之间的差值逐渐变大,此时迭代次数略微增加。但是预测偏差的变化并未对主从博弈迭代次数产生过多影响。在下一步的工作中,将针对大规模互联微网,深入探究可再生能源出力不确定性对微网间主从博弈的影响。
3.2.3 对比分析
为了验证所提模型的有效性和经济性,将以下调度策略进行对比分析:策略1以微网经济性为目标,微网间无电能交互且不考虑需求侧负荷同时不计及需求侧满意度;策略2在策略1的基础上考虑微网间电能交互;策略3在策略2的基础上考虑需求侧负荷同时计及需求侧满意度(本文模型)。下面将从微网与配电网之间的电能交互和微网经济性两个方面进行分析。
(1)微网与配电网之间的电能交互结果分析。MG1与配电网之间的电能交互结果如图12所示,其余微网的仿真结果如图13。
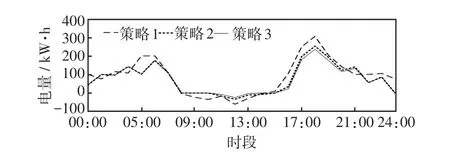
图12 微网MG1与配电网之间的电能交互Fig.12 Electricity interactions between microgrid MG1 and distribution network
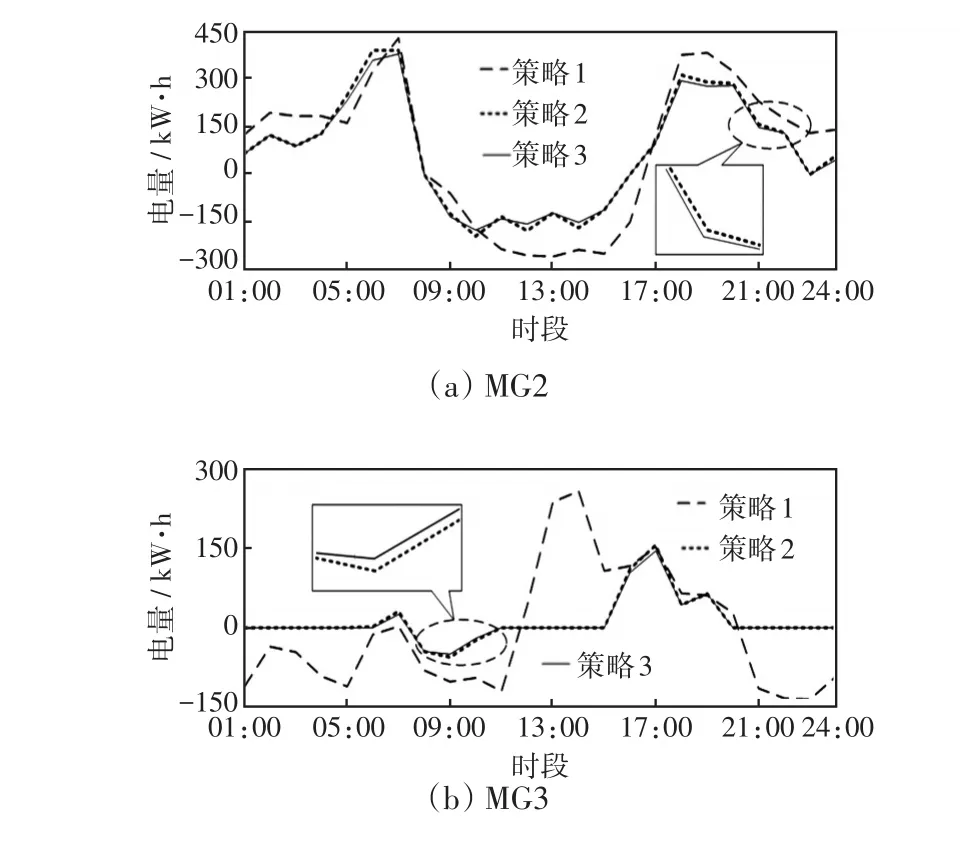
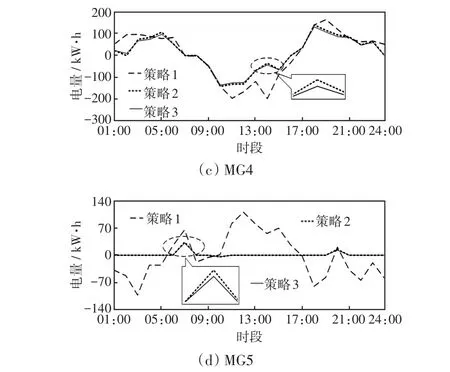
图13 其余微网与配电网之间的电能交互Fig.13 Electricity interactions between the others microgrids and distribution network
从图12可以看出,相比于策略1,在策略2和策略3下MG1与配电网间的交易电量均明显减小。当计及微网间电能交互时,在市场均衡的情况下,MG1可以向其他微网购买或出售电能,从而有效减小微网与配电网之间的交易电量,降低多微网接入给配电网造成的影响。此外,通过比较策略2和策略3可以发现,在时段11:00—14:00和时段16:00—21:00,策略3下MG1与配电网之间的交易电量有所减小。该现象表明,需求侧负荷能够有效促进微网间电能交互,充分消纳过剩可再生能源。
(2)微网经济性。三种策略下微网的运行成本如表2所示。由此可得,策略1下各微网的运行成本最高,策略3下各微网的经济性最优。由于微网间的电能交易价格介于配电网的购售电价之间,故通过促进微网间电能交互能够明显提升系统经济效用。以MG1为例,相比于策略1,策略2下MG1的运行成本降低了7.6%;相比于策略2,策略3下MG1的运行成本降低了1.8%。对多微网系统而言,三种策略下多微网系统的总运行成本依次降低10.8%和2.3%,提高了系统运行经济性。
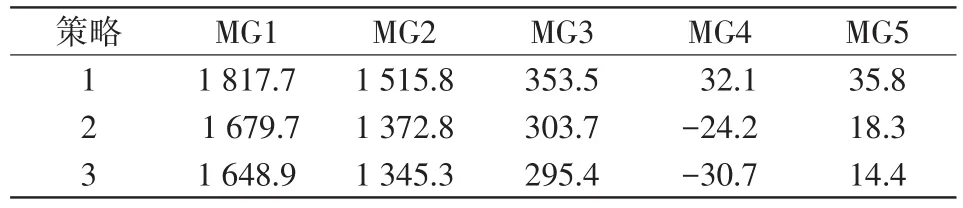
表2 微网的运行成本Tab.2 Operating costs of microgrids元
4 结论
本文提出了考虑多主体主从博弈的多微网协调优化模型,并验证了博弈模型的收敛性,以及对比分析了不同调度策略下的优化结果,最终得出以下结论:
(1)实时博弈阶段可以较快地在发电微网和用户微网之间形成基于动态定价的电能交易策略,提高系统经济效益,促进系统供需平衡;
(2)所提模型通过日前和实时两阶段协调优化减小了可再生能源出力波动性对系统造成的影响。
此外,通过计及微网间电能交互及需求侧负荷实现了可再生能源的充分消纳,降低了多微网对配电网的依赖性,确保了系统安全稳定经济运行。
