基于定位概率和收缩机制的电力系统拓扑演化模型
2021-01-29葛贤军汪惟源孙文涛
孙 珂,王 丹,葛贤军,汪惟源,孙文涛
(1.国网经济技术研究院有限公司,北京 102209;2.电力系统及发电设备控制和仿真国家重点实验室(清华大学电机系),北京 100084;3.国网江苏省电力有限公司,南京 210019;4.国网江苏省电力有限公司经济技术研究院,南京 210008)
随着可再生能源、综合能源和能源互联网的快速发展和接入电网,泛在电力物联网、数字电网时代正在成为可能。传统的电力系统网络结构和运行方式已发生了非常大的变化,源-网-荷-储等多类型参数不确定性越来越多,电网的运行特性和动态行为特征更为复杂,系统运行状态分析和控制难度大大增加,尤其是电力系统拓扑结构的动态性变强,值得深入研究。
为有效实现对复杂电网拓扑结构的定量分析,通常的做法是:首先,对电力系统的电压、电流等物理原理进行定性分析;然后结合电力系统母线、变压器、线路、开关、断路器等各类型器件的运行特性和彼此的关联关系,以频率和电压稳定为基础,构建拟分析电力系统网络的动态数学模型,并设定边界条件后应用数学求解算法进行仿真分析;最后实现电力系统各个组成元件之间关系定量描述,完成拓扑结构分析。然而,当前以上方法不再完全适用,其主要原因是:①电力系统网络结构具有动态性,即网络中的分布式电源、微电网、综合能源系统等电源,电动汽车、储能等柔性负荷,以及它们之间的连接是动态的,从而导致电力系统的网络方程或者数学模型也随之动态;②具有电源和负荷双重特性的电动汽车、储能、微电网、综合能源系统等元件或子系统规模化接入电力系统,电源和负荷之间的变换成为常态,电力系统网络建模面临多源-多网-多荷的动态运行挑战;③根据电力系统实际运行情况,所构建的网络动态数学模型极其庞大、维度高,对其计算分析的难度相当高,而且对计算精度和速度等性能的要求也极高,难以满足实时要求;④为满足电力系统运行实时性需求,在电力系统建模过程中,通常会对电力系统网络结构中的部分元件或者子系统进行一些等值简化,从而降低了结果精度,无法全面体现系统的运行特性;因此,建立一种合理有效的电网动态模型,实现对它的动态特性进行分析,非常必要。
在电力系统拓扑分析建模方面,国内外专家和学者们基于复杂网络理论[1-10]提出了一些分析模型,主要包括NW(Newman-Watts)随机网络模型、WS(Watts-Strogatz)小世界模型、无标度网络模型等。另外,一些学者也通过复杂网络理论来寻找电网拓扑结构的薄弱点,从而实现对电力系统的鲁棒性和脆弱性分析,以及探索可能存在的大规模断电故障、系统奔溃等问题[11-19],其核心目标是保证电力系统的可靠、安全、经济、稳定运行。但是整体而言,目前基于复杂网络理论的算法和模型,主要聚焦于系统的“生长”过程,较少考虑系统的精确描述,无法较好从电力系统的规划设计、网架坚强性提升、故障精准预测与恢复等方面,实现对电力系统网络宏观特性的定量分析;当电力系统运行过程中由于故障、经济调度等导致拓扑结构发生变化时,现有的分析模型已经较难实现有效分析,有些模型甚至出现错误结果。
1 电网拓扑动态演化建模
电力系统中含有分布式电源和可再生能源、电动汽车等多类型用户负荷和铅酸、锂电等不同类型储能等,这些新型源-荷-储元素在实际运行过程中并网或者离网具有实时动态性,使得对电力系统中任意节点的拓扑变化进行准确地定量分析难度大。为有效实现电网的资源优化配置和运行效率提升,本文拟采用“位置链接概率”来分析电力系统网络拓扑的初始模型,下面进行详细阐述。
1.1 位置连接概率
为对任意两个节点之间的位连接概率进行表征,先设定欧式问题空间中任意的两个节点i和j,它们的坐标分别为(xi,yi)和(xj,yj),则该两点之间的欧氏距离为
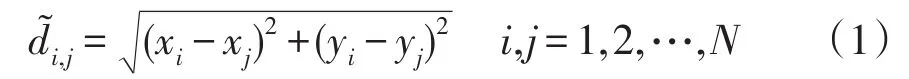
式中,N为网络中节点的总个数。
同时,设定欧式网络空间中任意两个节点之间的最大欧氏空间距离,如式(2)所示。

欧式网络空间中任意两个节点i和j之间的位置链接概率p(i,j)为
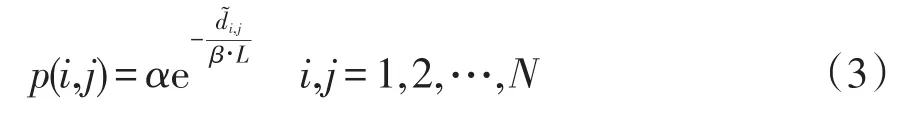
式中,α、β是取值范围为(0,1]的调节参数。
电力系统拓扑结构发生变化实现动态演化,拓扑结构中的任意一个节点连接关系变化具有以下常识:①电源、负荷及网络中任意的一个节点都会根据自身运行的不同需求进行并网、离网等重构工作;②依据电力系统动态运行特点,新的电源或者负荷节点加入网络拓扑,具有随机性;③网络中的任意一个节点均可能随时由于故障原因,实时断开与它连接的所有节点,自身形成孤岛运行。因此,以概率p1、p2和p3分别表示电力系统网络拓扑结构中增加节点、重连节点、断开和孤立节点等三种重构行为,并且p、p2和p3需满足式(4)、(5)的约束。

其中,式(5)确保了电力系统网络结构中总节点数目为增长的趋向,从而可确保电力系统网络不会随着演化的过程解裂为离散点,导致无法构成正常运行的网络,式(5)的约束也正好反映了真实的电网在演化过程中可一直保持电网的动态稳定平衡。
1.2 电力系统动态演化模型
在实现对电力系统任意节点连接概率定量表征的基础上,为有效分析电力系统拓扑结构中所有节点的推演变化,设计了电力系统拓扑结构的收缩机制推演模型,实现的主要步骤如下:
(1)初始化网络。首先,构建出拥有Nstart个节点和M条边的初始网络,而且节点之间的连接概率应该满足式(3),且电力系统网络的边数M应满足

(2)新增节点。以概率p1新添一个电力系统网络拓扑节点,且该节点与原来已存在的节点彼此连接,并形成m1条边;
(3)重连节点。以概率p2随机挑选电力系统网络中原有一些节点的m2条边,让这m2条边与其他节点发生随机的重连操作;
(4)删除节点。以概率p3随机删掉电力系统网络中的任意一个节点,且删除与该节点相连的所有边;
(5)终止操作。在每一次的操作过程中,以概率p1、p2和p3,挑选以上(2)、(3)、(4)中的任意一个步骤来执行操作,并一直进行收缩循环执行,直到所操作的次数达到电力系统网络拓扑中的节点个数预先设定值Nend为止。
按照以上基于收缩机制的电力系统动态演化模型步骤,设定位置连接概率的调节参数α,β初始值分别为0.1和0.3,总节点数为Nstart=20,分析节点为20的初始电力系统网络结构的推演过程,其结果如图1所示。
依次类推,按照电力系统动态演化规律的步骤,分别对终止节点总数的IEEE 57、118和300的三种电力系统网络结构进行推演,其结果如图2所示。
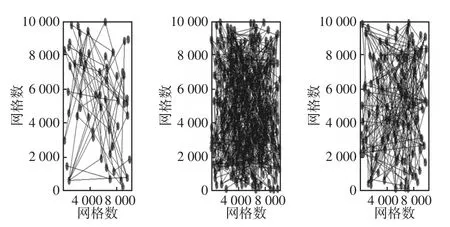
图2 IEEE 57、118和300节点网络模型演化结果Fig.2 Evolution results of IEEE 57,118,and 300 node network models
2 动态演化模型拓扑特性分析
图1和图2的结果,可以一定程度上说明电力系统的拓扑结构整体节点总数的基本演化过程,但无法完成网络内部任意一个节点变化情况描述,缺乏有效的定量分析指标。为此,为有效衡量动态演化模型的量化特征,提出相关的评价指标,主要包括平均路径长度、聚类系数、节点度和网络的度分布等4个指标。
(1)平均路径长度L为

式中:di,j为系统网络拓扑中任意两个节点为i和j之间的距离;N是电力系统网络拓扑的总节点数。
(2)设电力系统网络拓扑中任意一个节点i与ki个节点相连,即节点i拥有ki条边,则该节点的网络聚类系数C为
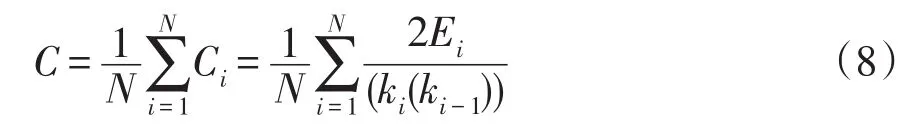
式中:Ei为其他ki个节点它们之间相连接的总边数;Ci为节点i自身的聚类系数。
(3)设定节点度k是指电力系统中任意节点i拥有边的条数k;网络的度分布P(k)是指电力系统任意一个节点其节点度为k的概率。由公式(4)不难发现,整个电力系统网络拓扑中所有节点度分布的之和应当满足,其中,Pi(k)表示网络拓扑中任意节点i的度分布。为此,从常识可知在复杂网络中,节点度k的值越高,说明该节点与其他节点连接越多,也说明与该节点相连的边越多。
2.1 节点度分布特性分析
进一步,为了表征本文所提动态演化模型中度分布的时变规律。假设任意时刻t,度分布值为k的电力系统网络拓扑中任意节点度分布概率为P(k,t)。针对新增节点,设定网络拓扑中新添加任意一个节点,有且仅有带入一条边,由参考文献[15]可知,该节点的度分布概率Pa(k,t)为
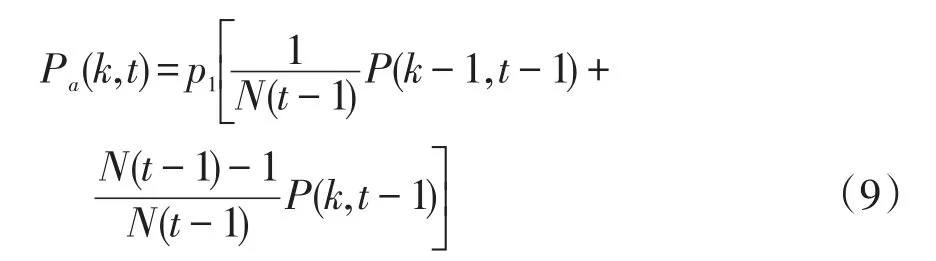
式中:N(t-1)为电力系统网络中(t-1)时刻节点的总数目;P(k-1,t-1)为电力系统网络中该节点上一个(t-1)时间的节点度分布概率。
同理类推,针对重连节点,假设任意时刻t,网络拓扑结构中任意一个节点i的一条边从节点i与另一个节点j相连,则此时该节点的网络度分布概率Pr(k,t)为
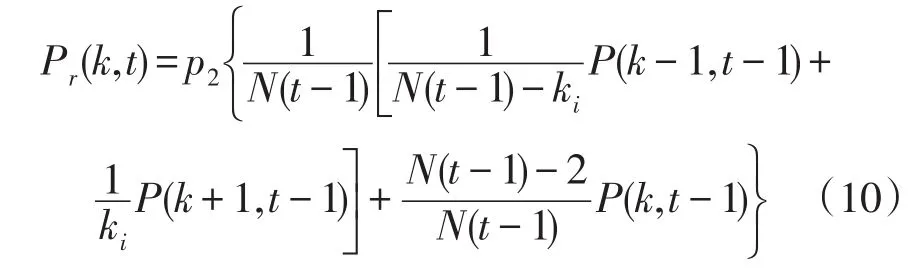
进一步,假设任意时刻t电力网络中的一个节点i,将与该节点i相连接的所有边都被删除,则该节点删除连接后的网络度分布概率[15]为

联合节点连接概率约束方程(4)、(5),任意t时刻,电力系统网络度分布概率P(k,t)的递推表达式为

此处需要说明的是,为了确保式(12)的普便适用价值而不失一般性的特征,进行如下约定:①假定任意时刻t内,任意新添的节点i仅仅相应的增加一条边;②每一个节点i也都仅有一条边从该节点重新连接到另一个节点j;③一旦电力系统拓扑结构中存在多条边的变化,可将其视为分多步执行。
根据2.1的原理,分别对IEEE 57、118和300节点进行度分布特性分析,结果如图3所示。从图3不难发现,该模型的网络度分布具有幂律分布的特性,即IEEE三种拓扑结构中均出现某些节点度要比其他节点大得多。这些度分布比较大的节点与网络中的其他节点连接相对紧密,跟其他节点的能量交换相对比较容易,是网络拓扑结构中相对“特别重要”的节点;这些节点一旦受到攻击或者损坏,将可能导致电力系统的奔溃、解裂等,它们对电力系统鲁棒性提升、安全性加强等意义重大。
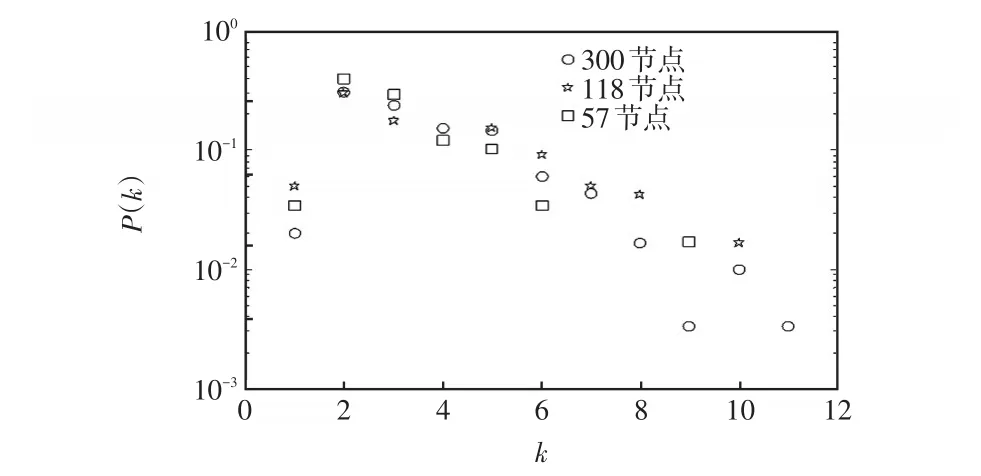
图3 IEEE 57、118和300节点网络的度分布情况Fig.3 Degree distribution of IEEE 57,118and 300 node networks
2.2 动态网络模型评估
为验证节点连接概率在电力系统拓扑结构推演过程中的作用,选取节点连接概率调节参数α,β为0.1和0.3,分别对IEEE 39、IEEE 57、IEEE 118、IEEE 162和IEEE 300等不同标准测试系统进行分析,其结果数据见表1。从表1中不难发现,通过选取不同的调节参数,不同的标准测试系统具有一定的规律。
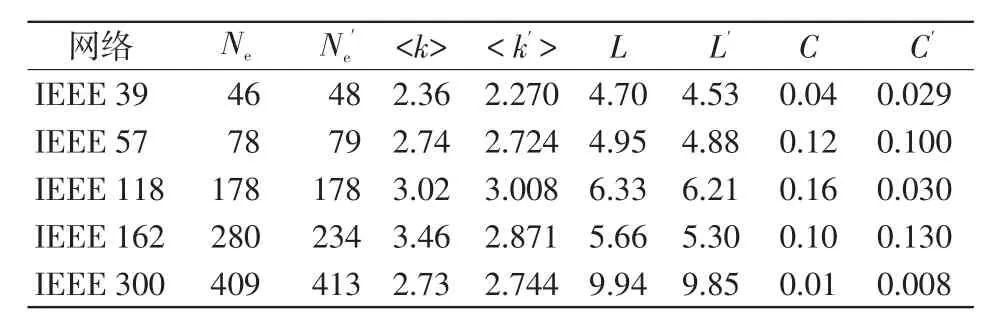
表1 IEEE标准电力系统和本文推演模型评价指标值对比Tab.1 Comparison of evaluation index values between IEEE standard power system and the proposed evolution model
表1中:Ne、<k>、L、C分别为IEEE 标准测试系统的网络总边数、平均度数、平均路径长度和网络聚类系数;、<k′>、L′、C′分别本文所提出的推演模型仿真所得的相对应结果。
设定调节参数α和β分别为0.2和0.3,初始网络节点数为Nstart=20,则IEEE 57、118和300标准系统的网络聚类系数与网络节点的总度数如图4和图5所示。
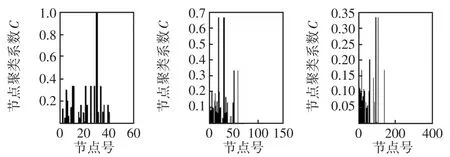
图4 IEEE 57、118和300网络节点的聚类系数Fig.4 Clustering coefficients of IEEE 57,118 and 300 node networks
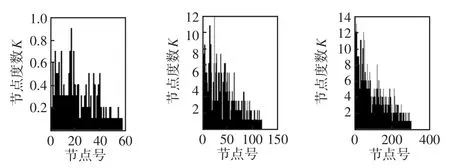
图5 IEEE 57、118和300网络节点的节点度数Fig.5 Node degrees of IEEE 57,118 and 300node networks
从图4不难发现,在三种标准测试算例的网络拓扑中有一些节点的聚类系数为0,即这样的节点与其他节点相连的边数非常少,从而也印证了这样节点的外部连接非常弱、鲁棒性较差,最好不要作为电源节点,特别是当将其作为重要的供电电源节点时,一旦受到攻击,风险较大。反之,拥有高聚类系数的节点,说明该节点与电力系统网络中其他节点联系紧密,当电力系统网络中此类节点受到攻击,可以通过与它有密切彼此联系节点的转供,实现电网的稳定运行,相对比较适合选作电网的枢纽点,能有效提升系统供电可靠性。当然,当分布式能源出力过大,还可考虑将分布式电源产生的多余能量,利用铅酸、锂电池等储能设备先将它们储存起来,然后在系统负荷高峰时,进行放电补充电网缺口,从而达到系统可靠供电。
同理,在图5中,也存在一些节点的度分布值比较高,这些度分布值较高的节点也是其电力系统网络运行中的“重要节点”,从系统稳定运行角度出发,可选作为主要供电电源或重要用电负荷的安放点。
2.3 模型可靠性分析
电力系统运行过程中故障、运行调度等将会使一些节点与系统解列,即删除节点。为此,为分析在电力系统网络拓扑动态演化过程中,概率p3删除节点变化对电力系统网络拓扑的运行特性的影响大小,下面详细阐述。
依然以IEEE 57、IEEE118、IEEE162和IEEE300节点标准测试系统为例,图6、7、8、9分别是IEEE 57、118、162和300标准测试系统的总边数、网络平均路径长度、网络聚类系数及总节点度数等4个指标的变化趋势曲线,按照概率p3删除节点,分析其变化趋势。
从图6~图9,不难发现:
(1)由图6知,删除概率p3值越大,电力系统网络拓扑的总边数就越少;反之,如果删除概率p3值越小,电力系统网络拓扑的总边数相对较多,删掉电力系统网络中的节点对其影响相对较小。
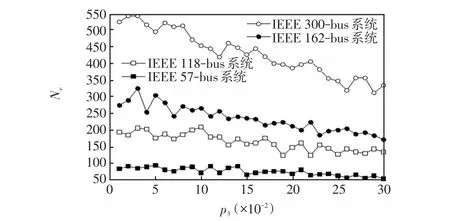
图6 IEEE标准测试算例的网络总边数随p3变化情况Fig.6 Changes in the total number of edges in IEEE standard test example withp3

图7 IEEE标准测试算例的平均路径长度随p3变化情况Fig.7 Changes in average path length of IEEE standard test example withp3

图8 IEEE标准测试算例的聚类系数随p3变化情况Fig.8 Changes in clustering coefficient of IEEE standard test example withp3
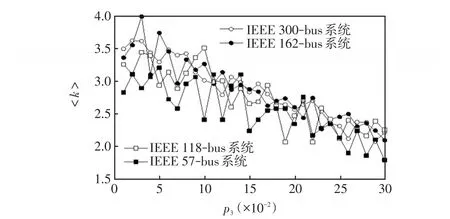
图9 IEEE标准测试算例的总节点度数随p3变化情况Fig.9 Changes in total node degree of IEEE standard test example withp3
(2)从图6还可知,网络拓扑节点数越多,它的斜率比节点数少电力系统网络的斜率要大,其主要原因是最终节点数多的网络,它的每一个节点会与电力系统网络中的节点有相对较多的相连,从而会得到更大的度分布值。说明删除节点对网络拓扑影响大。
(3)从图7可知,删除节点的概率p3值越大,网络中平均路径长度越短,但其曲线的波动范围相对较小,表明网络中删除节点,对节点之间的最短路径距离影响相对小。
(4)从图8可知,概率p3的删除节点变化对电力系统网络聚类系数的影响并无明显规律,是一种毫无明显特征的波动曲线,仅仅呈现一定的波动规律,即电力系统网络节点越多,其曲线波动相对较小,因此说明:节点总数较大的电力系统拓扑结构相对比较复杂,此时一些节点的删除或者退出运行对网络拓扑中节点之间的交叉联系影响不大,也印证了电力系统网络越复杂,一旦节点失电,实现对该节点的转供电概率相对越高。
进一步,近年来国内外的专家和学者们通过大量的仿真实验还发现,节点删除概率p3值不能无限扩大至1(全部删掉,系统停运),其上限应小于0.32,即p3<0.32,一旦删除节点概率值大于0.32,网络解裂的速度就会大于连接的速度,将会导致整个网络崩溃,此时无论电力系统网络结构多复杂,其最终结果将是系统的不稳定,从而也印证了作为刚性特点的电力系统,其稳定是有边界的。
当然,电力系统在运行过程中一般拥有一定面对多类型故障的承受和自愈能力,即电力系统的鲁棒性。进一步,结合现在电力物联网的特点,下面从系统抗随机故障、抗主动攻击等两个维度,应用本文所提出的电力系统动态演化模型来分析系统的鲁棒性。分别模拟系统抗随机故障和抗主动攻击两种故障类型,计算IEEE 57、118和300节点电力系统中受影响节点数量,其曲线如图10所示。

图10 随机故障与主动攻击对IEEE标准测试系统节点的影响Fig.10 Effects of random failures and active attacks on nodes of IEEE standard test systems
从图10不难发现。
(1)主动攻击的对象选取最大度数的电力系统网络节点为最佳,一旦此类电力系统节点受到攻击,与其连接的节点变为删除节点,系统的整体鲁棒性大大降低。因此,在实际电力系统主网架结构搭建过程中,在这些关键网络节点上配置冗余和保护机制,可有效提升系统可靠性。
(2)随机故障与主动攻击相比,系统的鲁棒性更强。其主要原因是随机故障具有强突发性,故障点大概率发生在一些非重要节点,此时对电力系统的影响有限。这也印证了电力系统具有一定的弹性。
(3)随着IEEE 57、IEEE118和IEEE300节点总数增多,其网络系统的鲁棒性会相应的增强,这与2.3节中删除节点对电力系统影响的作用所获得的结论基本一致,从而也印证了互联互通的复杂电力系统稳定性更强。
(4)在电力系统主网架结构的规划和设计阶段,应尽可能减少对个别重要节点的依赖作用,通过增加节点之间的互联互通,形成电力系统多个枢纽节点共存态势,实现电力系统可靠性提升。
(5)本文所提模型可定量分析电力系统网络拓扑节点对可靠性的作用。根据计算结果对关键节点安装设备和加强保护,实现电网整体运行的安全性提升,并节约了投资建设成本。
3 结语
本文提出了一种基于定位概率和收缩机制的的新型网络建模方法,通过采用复杂网络度量来评估和揭示电力系统网络拓扑的关键统计学特性。所提出的动态演化建模方法可从拓扑角度对电力系统的演化特征和复杂动态行为进行分析。此外,所提出的网络模型,也可以对电网的系统鲁棒性和脆弱性进行系统化的评价和分析。
着眼未来,电力系统网络拓扑推演模型可着重从以下两个方面进行开展深入研究:一方面是基于真实的电力系统运行状态对所提出的模型进行验证和分析;另一方面,可将电网的可靠性分析和级联故障传播机制纳入所提出的模型,从而有效提升电网络规划的有效性和运行的可靠性。
