不同岩性的机制砂混凝土本构关系及力学性能
2021-01-29谢开仲刘振威盖炳州朱茂金
谢开仲,刘振威,盖炳州,新 赢,朱茂金
(1. 广西大学土木建筑工程学院,广西南宁 530004; 2. 广西大学工程防灾与结构安全教育部重点实验室,广西南宁 530004)
0 引 言
机制砂混凝土是指将机制砂部分或全部代替天然细骨料所制成的混凝土。由于机制砂是岩石通过机械破碎而制成的筛分粒径小于4.75 mm的岩石颗粒,这使得机制砂与河砂相比具有不规则的棱角尖边、较高的石粉含量和较粗糙的表面等不同的特征,因此对混凝土工作性能及力学性能有着不同程度的影响[1-6]。近几年来,国内外学者对不同材料的混凝土本构关系展开了深入的试验研究,如肖建庄等[7]和陈宗平等[8]发现,随着再生粗骨料取代率增加,再生混凝土峰值应力和弹性模量均呈下降趋势,但应力-应变曲线下降段相比于普通混凝土更加陡峭,破坏形式为脆性破坏。赵秋红等[9]和Bompa等[10]指出橡胶混凝土的峰值应力、峰值应变、弹性模量都随着橡胶含量的增加而降低,并建立了适用于橡胶混凝土的本构模型。叶中豹等[11]对钢纤维混凝土进行试验研究,发现钢纤维含量的增加使得混凝土的峰值应变与峰值应力都随之提高,并提出了一种与应变和应变率相关函数的本构关系。对于机制砂混凝土方面,陈正发等[12]指出机制砂混凝土的应力-应变关系呈现非线性表征,并在Jones-Nelson-Morgan模型的基础上引入温度系数,建立了机制砂混凝土的单轴受压本构模型;梁冬瑶[13]以机制砂作为细骨料,对不同石粉含量的再生混凝土进行研究,并结合损伤力学的理论方法,得出机制砂混凝土本构方程在各变量下的参数。
目前对不同岩性机制砂混凝土的本构关系和力学性能的研究较少,基于上述分析,本文以机制砂为细骨料,以母岩岩性的机制砂及强度等级为研究变量,与河砂混凝土进行对比分析,通过试验揭示其内在特性,获取各变量下的参数,建立机制砂混凝土应力-应变本构方程,为机制砂在混凝土工程中的应用提供技术指导。
1 试验概况
1.1 原材料性能试验
为了开展机制砂混凝土相关研究,首先将不同机制砂母岩块石经过切割、打磨加工成70 mm×70 mm×70 mm抗压试块和φ50×50劈裂试块,根据《公路工程岩石试验规程》(JTG E41—2005)开展岩石试验研究,其母岩的力学性能见表1,机制砂母岩强度从大到小依次为卵石、玄武岩、石灰岩。
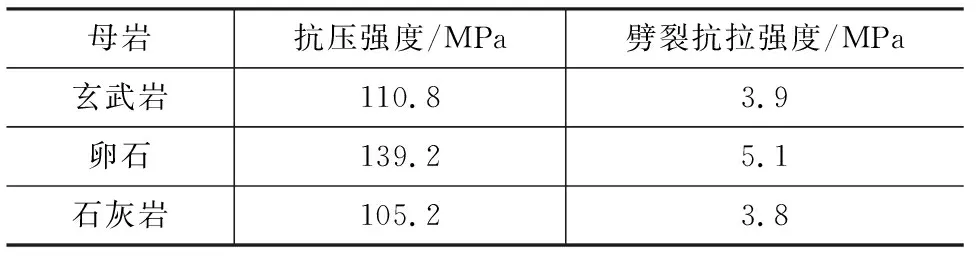
表1 母岩的力学性能Tab.1 Mechanical Properties of Parent Rock
不同岩性的机制砂母岩经机械破碎分别得到石灰岩机制砂(LS)、卵石机制砂(PS)和玄武岩机制砂(BS),并采用河砂(RS)进行对比,根据《建筑用砂》(GB/T 14684—2011)对不同细骨料的颗粒级配、表观密度、堆积密度、含泥量及机制砂中石粉含量等性能指标进行了测试,主要性能指标见表2,细骨料均为Ⅱ区级配,机制砂的表观密度、堆积密度和石粉含量均高于河砂,而细度模数和孔隙率较低。机制砂的表观密度、堆积密度和石粉含量从大到小依次为石灰岩机制砂、卵石机制砂、玄武岩机制砂。
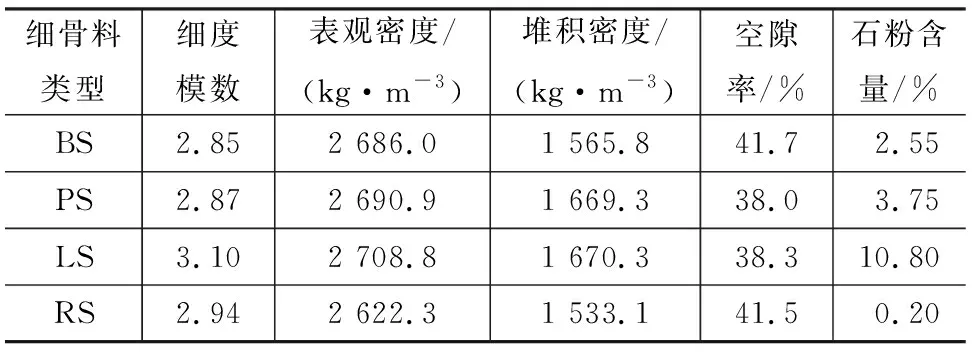
表2 机制砂与河砂的物理特性Tab.2 Physical Properties of Manufactured Sand and River Sand
研究中使用的粗骨料粒径为4.75~31.5 mm连续级配的石灰岩碎石,按照《建筑用卵石、碎石》(GB/T 14685—2011)的规定对碎石的颗粒级配、表观密度和堆积密度等进行了测试,其物理性能均符合要求。水泥采用的是P.O42.5海螺牌普通硅酸盐水泥,经检测其性能指标均达标。试验用的外加剂为聚羧酸高性能减水剂,减水率为30%,试验用水为自来水。
1.2 试验方法
1.2.1 配合比设计
参照《普通混凝土拌合物性能试验方法标准》(GB/T 50080—2016)对不同岩性机制砂混凝土的工作性能进行测试,在强度满足要求的情况下略微调整水灰比与砂率,保证坍落度达到160~180 mm,得到的机制砂混凝土基准配合比见表3。
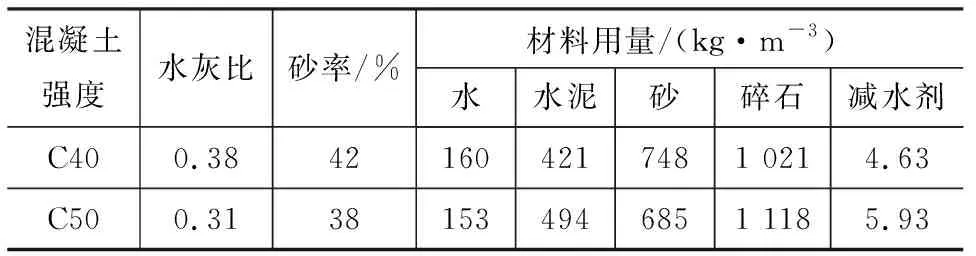
表3 机制砂混凝土配合比Tab.3 Mix Proportions of MSC
1.2.2 试件制作
试验采用3种不同母岩岩性的机制砂和河砂作为细骨料,共制作了48个混凝土试件,每组共设计了3个150 mm×150 mm×300 mm标准棱柱体试件和3个150 mm×150 mm×150 mm标准立方体试件,前者用于测出混凝土应力-应变本构关系,后者为了测出混凝土立方体抗压强度,混凝土试件浇筑24 h后脱模,在标准养护室内养护28 d后进行单轴加载试验。
1.2.3 试验加载装置及方法
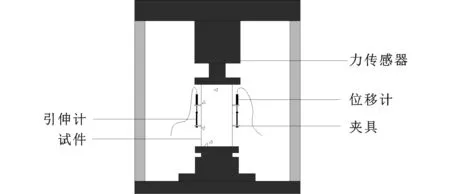
试件采用由中科院和SIMENS公司联合研发的RMT-201岩石与混凝土力学试验机进行单轴受压加载,测点布置及加载装置见图1,2。为了获取试件受力全过程的应力-应变(σ-ε)曲线,试验采用荷载和位移混合控制的加载制度,即试验先采用荷载控制加载到试件预估峰值的70%,加载速率为10 kN·s-1;后采用位移控制的加载制度施加竖向荷载直至试件破坏,加载速率为0.005 mm·s-1。本试验位移的采集选取试件中间100 mm的混凝土竖向变形作为测试结果,对试验机自动采集的各试件受力轴向荷载-位移曲线进行相关处理,得到试件的应力-应变全过程曲线。立方体抗压强度根据《普通混凝土力学性能试验方法标准》(GB/T 50081—2002)采用电液伺服万能试验机进行单轴加载试验。
2 试验结果及分析
2.1 标准龄期棱柱体抗压强度
2.1.1 破坏形态
试验过程中,分别对不同岩性的试件进行细微观察发现,3种不同岩性的机制砂混凝土试件的破坏形态基本相似,均表现出较大的脆性。在荷载控制阶段,随着压力荷载的不断增大,试件的中间部分首先由无肉眼可见的裂缝逐渐形成1条贯穿的主裂缝;在位移控制阶段,峰值荷载前,试件表面逐渐出现裂纹,裂纹沿上下方向延伸,峰值点过后,新的裂纹不断出现,旧的裂纹宽度也逐渐增大,混凝土承载力迅速下降,与河砂混凝土相比,石灰岩机制砂混凝土和玄武岩机制砂混凝土裂缝较多,每个试件破坏表面均有4~6条贯穿裂缝,卵石机制砂混凝土裂缝数目与河砂混凝土大致相同,原因可能是由于卵石机制砂的粒径分布均匀,砂中含有适量的石粉颗粒,有效地填充了混凝土孔隙,提高了混凝土的抗压性能,使得裂缝数目相对较少[14-15]。从破坏后的断面细致观察发现,所有试件的最终破坏界面均出现在粗骨料与水泥砂浆的界面过渡区,粗骨料本身未出现断裂,典型试件的破坏形态见图3。

2.1.2 应力-应变全曲线
根据RMT-201试验机自动采集的各试件受力全过程的轴向荷载-位移数据,通过式(1)可以转化得到各试件的轴向应力-应变(σ-ε)全过程曲线,如图4所示,其中BS,PS,LS和RS为细集料类型,40和50分别代表混凝土设计强度,“1”表示第1个混凝土试件,依此类推。
σ=N/A,ε=Δl/l
(1)
式中:N为试件的轴向荷载;A为试件的横截面面积;l为试件的标距,即位移计上下测点距离;Δl为试件标距内混凝土的轴向压缩变形值。
从图4可以看出,不同岩性机制砂混凝土的应力-应变曲线在相同的设计强度等级下变化过程大致相似,均经历了从弹性、弹塑性、峰值点、下降、下降段拐点到残余段的发展历程,函数图像为明显的凸曲线,在峰值点后的下降段,机制砂混凝土相比河砂混凝土的脆性大,尤其是当水灰比越小时,机制砂混凝土应力-应变曲线的下降段更加陡峭,其中卵石机制砂混凝土较为明显。
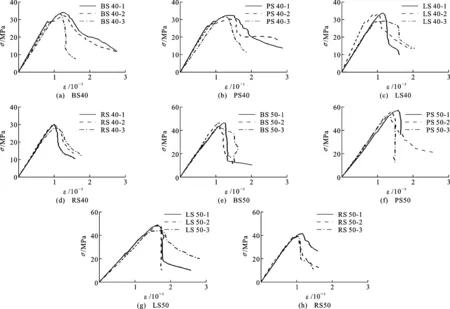
根据混凝土单轴受压下的应力-应变曲线可提取出各混凝土试件的峰值应力和峰值应变等特征值指标,每组试验数据均计算出3个试件的平均值,具体数值见表4。

表4 标准龄期下试件的峰值应力和峰值应变Tab.4 Peak Stress and Peak Strain of Specimens Under Standard Age
为了便于分析不同岩性机制砂细集料对其混凝土力学性能的影响,图5给出了3种不同岩性机制砂和河砂的细度模数和石粉含量(质量分数)。由表4和图5可见,随着石粉含量的增加或细度模量的增大,混凝土的峰值应力呈现先增大后减小的趋势。这是因为机制砂中的细颗粒在混凝土中具有良好的填充效果[16-17]。当石粉含量或细度模数超过一定范围时,在相同的水灰比下,机制砂中多余的细颗粒会吸收一部分自由水,使得混凝土中没有足够的浆体来包裹所有的集料,导致混凝土密实性较差,强度降低[18],特别是在强度等级比较高时,下降趋势较为明显,因此使得卵石机制砂混凝土的峰值应力在C50强度等级下比玄武岩机制砂混凝土和石灰岩机制砂混凝土分别大21.3%和17.9%。
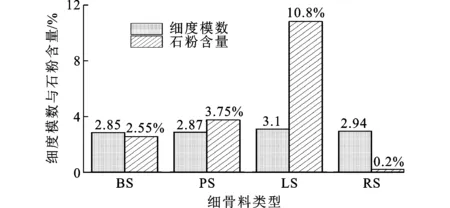
试件达到峰值应力时对应的峰值应变随着石粉含量的增加或细度模数的增大,也表现出先增大后减小的变化规律。当设计强度为C40时,卵石机制砂混凝土的峰值应变相比于玄武岩机制砂混凝土和石灰岩机制砂混凝土分别高13.7%和20.5%;当设计强度为C50时,石灰岩机制砂混凝土的峰值应变最大。原因是不同强度等级下,由于水灰比的不同,使得石粉参与水化反应后,黏附在粗骨料表面的水泥基有所不同,黏附的水泥基实际上是增加了凝固后混凝土的胶凝体含量,随着胶凝体含量的增加,试件的峰值应变也会有所增大[19]。
从表4和图5还可以看出,不同岩性机制砂混凝土试件的峰值应力与峰值应变均大于河砂混凝土试件。这可能是由于机制砂中含有的石粉促进了水泥水化,改善了混凝土的界面结构,使混凝土更加密实,强度得到提高。此外,机制砂中细骨料表面粗糙且多棱角,有效地限制了骨料颗粒间的滑动[1,6]。
2.1.3 机制砂混凝土本构方程拟合
根据试验实测的应力-应变曲线,在每一组试件中,抽取一个下降段数据较为充足的曲线进行量纲一化分析,8组试验数据分别取BS40-3,PS40-1,LS40-2,RS40-3,BS50-2,PS50-2,LS50-3,RS50-2对应的数值,将试验测得的应力-应变曲线进行归一化处理后,采用多种本构方程拟合量纲一化曲线,利用最小二乘法选取最佳的机制砂混凝土拟合本构模型,本次试验所选模型基于Sargin提出的普通混凝土单轴受压本构方程[式(2)][20],为了验证本构方程的适用性,分别对不同岩性机制砂混凝土和河砂混凝土应力-应变曲线进行拟合(图6)并与试验曲线对比。
(2)
式中:σc,εc分别为峰值应力与峰值应变;a1,a2和b1,b2分别为控制上升段和下降段的方程参数。
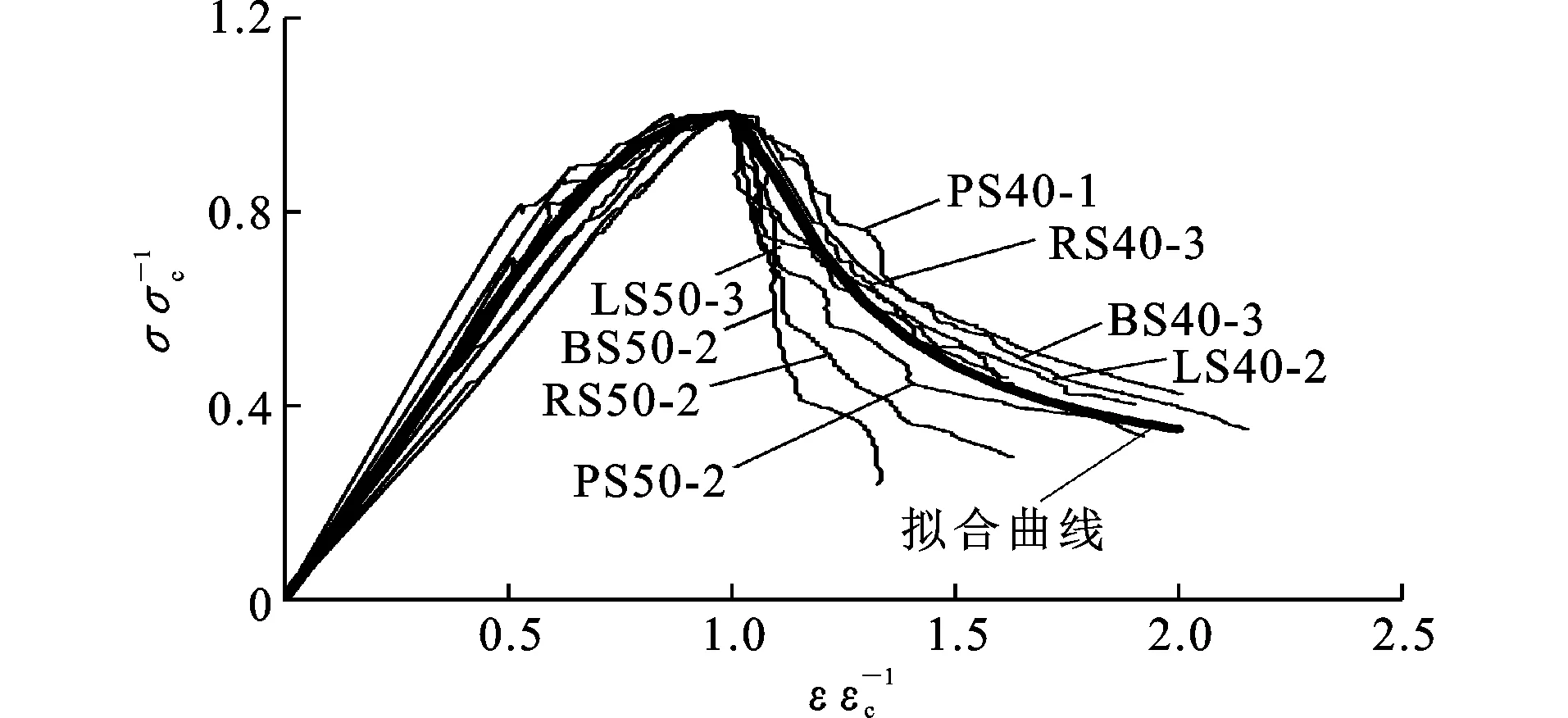
由图6可以看出,当a1=1.15,a2=0.51,b1=-0.19,b2=1.23时,拟合曲线与试验曲线的均值基本重合,这表明由式(2)所描述的全曲线方程可以作为机制砂混凝土单轴受压本构模型,适用于机制砂混凝土结构非线性分析。
2.2 标准龄期立方体抗压强度
2.2.1 破坏特征
随着压力荷载的不断增大,混凝土试件沿高度方向中央部位表面出现裂缝并逐渐变宽,然后裂缝往上下方向延伸,直到试件被压破坏,同时混凝土外鼓,裂缝主要集中在试件四角,试件的破坏面与竖直荷载方向大致呈45°角,最终的破坏形态呈正倒相接的四角锥形。
2.2.1 试验结果
混凝土单轴受压试验结果见表5,各类型的混凝土立方体抗压强度fcu均取其3个试件的平均值,其中棱柱体抗压强度fc取平均峰值应力。
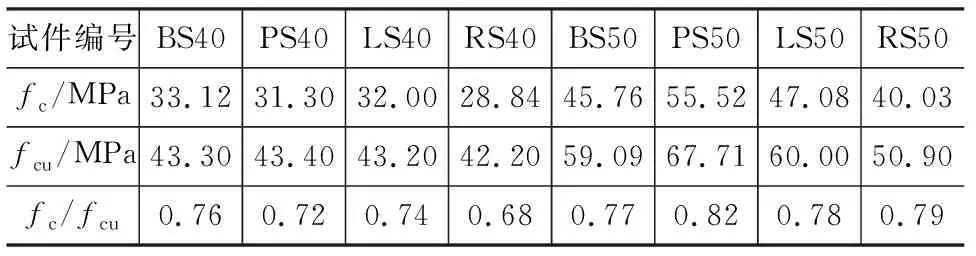
表5 标准龄期下棱柱体试件和立方体试件抗压强度的对比Tab.5 Compressive Strength Comparison Between Prism Specimens and Cube Specimens Under Standard Age
由表5可知,在相同强度等级下,机制砂混凝土抗压强度均高于河砂混凝土,特别是当设计强度为C50时,石灰岩机制砂混凝土和卵石机制砂混凝土的立方体抗压强度比河砂混凝土分别高16%和33%。原因是因为机制砂是由机械破碎得到,使得机制砂骨料表面织构凹凸、棱角分明,改善了砂与集料之间的界面,增强了界面之间的咬合力,使其与水泥之间具有较好的黏结性;同时,机制砂相比河砂中含有更多的石粉,石粉可以填充骨料之间的孔隙,使得混凝土变密实,强度得到提高[21-22]。
当设计强度为C40时,3种不同岩性的机制砂混凝土抗压强度基本相同。当设计强度为C50时,卵石机制砂混凝土的立方体抗压强度比石灰岩机制砂混凝土和玄武岩机制砂混凝土分别高12.9%和14.5%。这可能是由于卵石母岩的抗压强度较大,并且卵石机制砂中的石粉含量适量,能有效填充骨料之间的孔隙,增强了砂浆的流动性,提高了混凝土的和易性能,使混凝土的孔隙结构得到改善,混凝土更加密实[23-25]。
将轴心抗压强度与立方体抗压强度的比值定义为混凝土的换算系数,根据试验数据可以计算出不同岩性机制砂混凝土的换算系数,见表5。由表5可知:不同岩性机制砂混凝土换算系数在0.72~0.82之间,且平均值为0.767,变异系数为0.04,河砂混凝土换算系数为0.74,因此当水灰比在0.3~0.4之间时,建议机制砂混凝土换算系数取为0.77。
2.3 弹性模量
试验采取应力-应变全曲线上原点及0.40fc点之间的割线模量作为混凝土的弹性模量值,其中fc为棱柱体构件抗压强度;不同岩性机制砂混凝土试件弹性模量见图7。
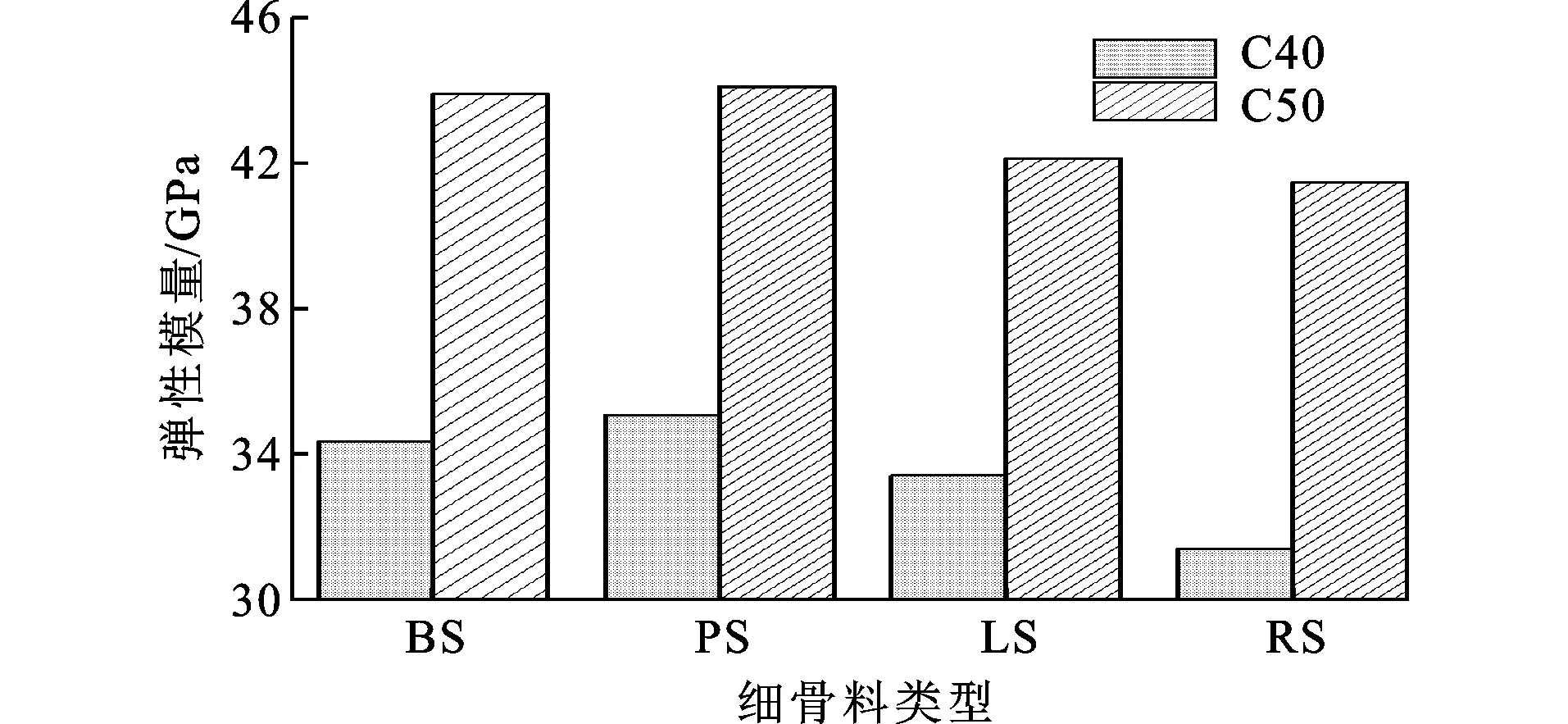
由图7可以看出:机制砂混凝土的弹性模量均大于河砂混凝土的弹性模量,最大差值比河砂混凝土高11.7%。不同岩性机制砂混凝土弹性模量曲线呈向下开口,当设计强度为C40时,PS混凝土弹性模量比BS混凝土和LS混凝土分别大2.1%和5.0%。机制砂混凝土的弹性模量与强度有关,一般而言,混凝土等级越高,弹性模量越大[26],正如前面分析所述,由于机制砂的颗粒形状、棱角凹凸以及石粉含量影响着混凝土的抗压强度,从而影响着混凝土的弹性模量。
根据《混凝土结构设计规范》(GB 50010—2010)的弹性模量计算式,对机制砂混凝土试验数据进行拟合,得到的拟合表达式为
(3)
式中:Ec为弹性模量。
弹性模量实测值与根据式(3)计算出的不同岩性机制砂混凝土弹性模量计算值见表6,其比值的平均值为1.001 2,变异系数为0.048 3,说明式(3)能够较好地表达机制砂混凝土的弹性模量随立方体抗压强度的变化趋势。
3 结 语
(1)不同岩性机制砂混凝土的破坏形态基本相似,与河砂混凝土相比,卵石和玄武岩机制砂混凝土裂缝数目较多,石灰岩机制砂混凝土裂缝数目与河砂混凝土大致相同。
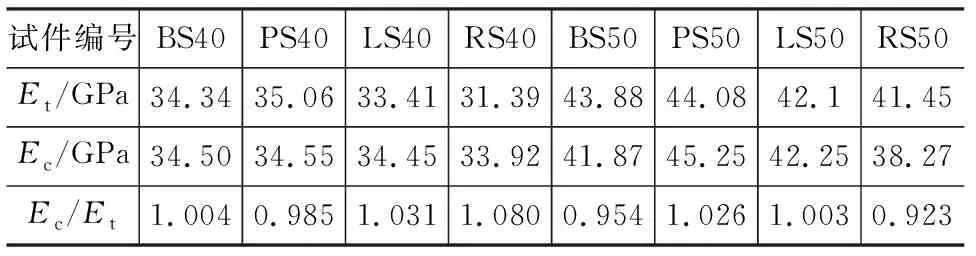
表6 弹性模量实测值与式(3)得到的弹性模量计算值Tab.6 Measured Value of Elastic Modulus and Theoretical Value of Elastic Modulus Calculated by Eq.(3)
(2)机制砂混凝土应力-应变曲线变化趋势与河砂混凝土相似,在曲线的上升段,机制砂混凝土与河砂混凝土基本重合,但在下降段,机制砂混凝土脆性较大,曲线比较陡峭,基于Sargin模型拟合得到的机制砂混凝土应力-应变全曲线与试验全曲线吻合较好。
(3)不同岩性机制砂混凝土力学性能的差异与细骨料的细度模数和石粉含量有关,随着细度模数或石粉含量的增多,机制砂混凝土试件峰值应力与峰值应变呈现出先增大后减小的趋势,不同岩性的机制砂混凝土试件其峰值应力与峰值应变均大于河砂混凝土。
(4)基于机制砂混凝土立方体抗压强度试验和轴心抗压强度试验的数据统计分析,当水灰比在0.3~0.4之间时,建议广西山区机制砂混凝土的换算系数取为0.77。
(5)卵石机制砂混凝土弹性模量高于石灰岩和玄武岩机制砂混凝土,并且机制砂混凝土的弹性模量大于河砂混凝土,基于试验数据,提出了机制砂混凝土弹性模量的计算表达式,计算值与实测值误差较小,能够较为准确地表达机制砂混凝土弹性模量随立方体抗压强度的变化规律。
