悬吊结构体系优化设计及减震性能研究

谭 平，兰 李，贺 辉，向 越，郑晓君

(1. 广州大学土木工程减震防灾省部共建协同创新中心，广东广州 510405； 2. 广州大学广东省地震工程与应用技术重点实验室，广东广州 510405； 3. 广州大学工程抗震减震与结构安全教育部重点实验室，广东广州 510405)

0 引 言

建筑结构隔震技术历经了数次地震的考验，已发展成一种成熟的结构减震控制方法[1]。Kelly等[2-3]对世界上隔震系统的历史发展和动力反应分析进行总结，指出铅芯橡胶支座和摩擦摆系统属于基础隔震中的领先技术，但仍有强震过后产生永久残余变形及制造和维护费用高等问题。Bakhshi等[4]提出了一种新的隔震技术，即悬挂摆隔震(SPI)系统。将上部结构安装在悬挂摆上，形成隔震体系，使整个系统几乎按摆长所决定的基本周期作刚体运动。SPI系统的优点是不管位移幅值多大，竖向荷载作用下是稳定的；另外，其设计、制造和安装过程都比较简单。通过实际震害调查可知，悬吊部分的空间摆动能改变了建筑结构的振动频率，使得悬吊结构体系能有效控制振动[5-6]。

针对悬吊结构体系，学者们对悬吊调谐及基础悬吊隔震进行了许多研究。悬吊调谐结构体系中，Gerges等[7]对一种钢索弹簧摆式调谐质量阻尼器的相关参数进行了试验研究，结果表明钢索弹簧应用于悬吊摆式调谐是一种经济可行的方案。Roffel等[8-9]通过对悬吊结构进行等效线性化，研究了有无阻尼情况下悬吊调谐质量阻尼器的最优参数。李宏男等[10-12]提出了利用悬吊质量摆来减小结构地震反应的方法，研究了悬吊质量摆-结构体系参数变化的影响，利用数值分析方法探讨了摆的不同悬吊方式及摆与结构质量比等因素对高层建筑结构地震反应的影响。对于基底悬吊隔震体系，Bakhshi等[4]针对一个由铅阻尼器支撑的SPI系统的比例模型进行了振动台试验，表明其能够有效地降低峰值加速度或峰值位移响应。王开才等[13]采用STAAD-Ⅲ有限元计算程序对等效处理后的悬摆隔震结构模型进行了动力计算分析，验证了悬摆隔震结构的减震效果是明显的。鲁亮等[14]在杆处设置竖向减震弹簧和耗能阻尼器，通过振动台试验验证了基底悬摆隔震结构三向隔震的有效性和可行性。

随着隔震层位置由上往下，结构体系表现出由调谐转变至基础隔震的减震机理[15]。Chai等[16]从控制角度对巨型子结构在地震和风荷载作用下的控制作用进行研究。谭平等[17]从巨-子结构控制体系的能量出发，对减震机理进行了验证。由于隔震层参数的选择对控制效果有很大影响，Tasake等[18]经分析得出结构层间位移随隔震层阻尼比的增大而减小。Ryan等[19]对不同隔震层位置及参数的层间隔震结构的隔震效率进行了比较；宋晓等[20]对其做进一步研究，通过十层框架结构的数值仿真，对比分析了基础隔震、层间隔震结构的减震效果。Villaverde等[21-22]对层间隔震结构参数优化等相关问题进行了探讨。王雪亮等[23]基于多性能目标，对混合结构的层间隔震进行参数优化设计，确定了木制隔震层的关键参数。

目前悬吊隔震结构理论研究大多涉及的是传统层间隔震及基底悬吊隔震，悬吊隔震层位于层间的研究还不充分。因此，本文对隔震层采用悬吊摆的悬吊结构体系进行研究，首先推导两自由度悬吊结构体系的运动方程及其等效线性化方程，综合考虑了上下部子结构位移响应，对结构体系进行参数优化。然后定义悬吊结构体系性能目标函数，以性能目标函数最小为优化目标，推导悬吊结构体系最优设计参数理论解。对相应系统进行参数分析，研究不同性能指数下，最优参数随质量比变化的关系。最后以某两层剪切型框架结构作为工程算例，通过数值分析进行验证。

1 悬吊结构体系分析模型

(1)

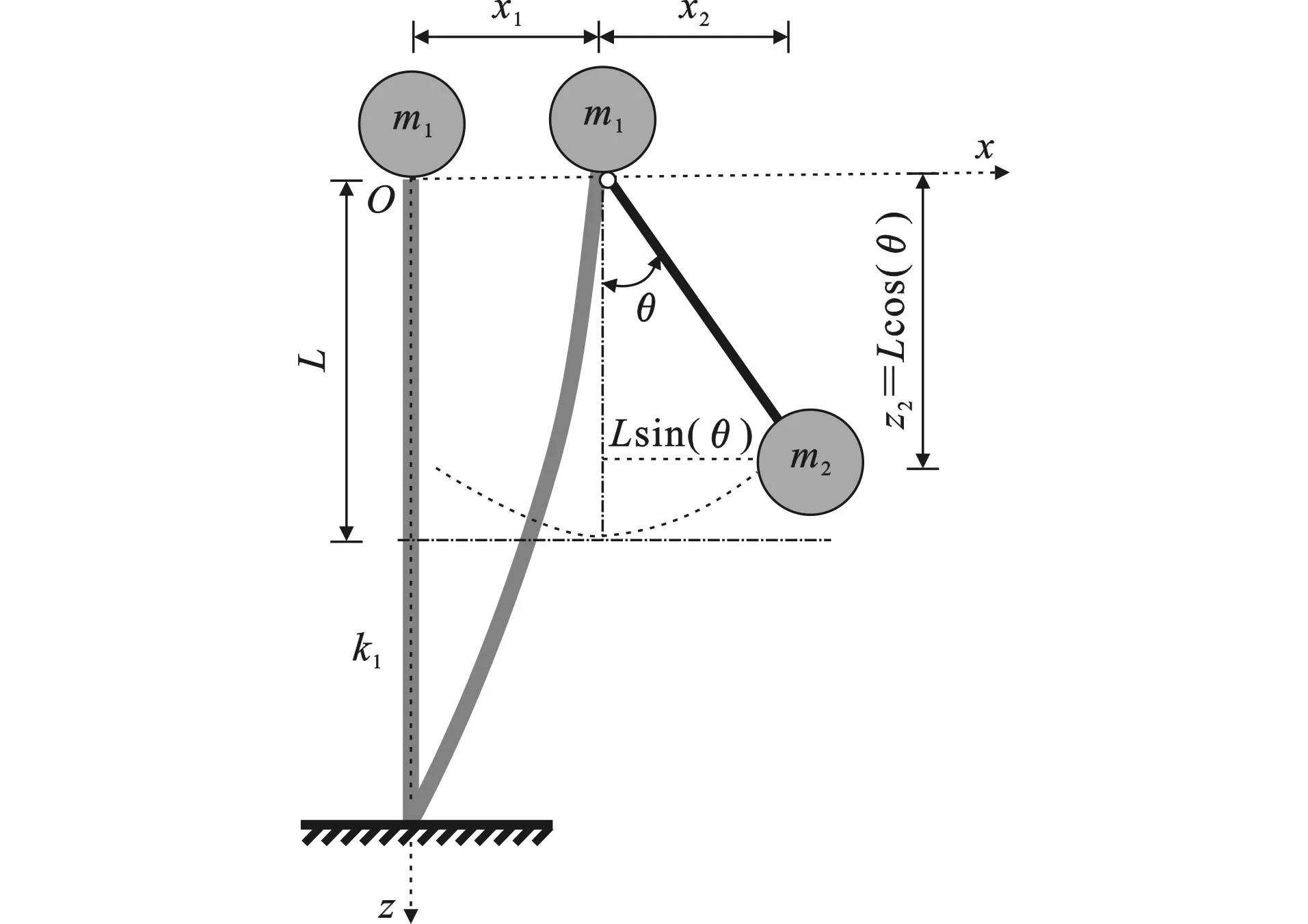
以x轴为重力势能零势能位置，则体系总势能V可表示为

(2)

式中：g为重力加速度。

进一步将非保守力做功δW表示为

(3)

将式(3)代入如下拉格朗日方程

(4)

式中：qi为广义坐标，即(x1，θ)，x1与θ均为时间t的函数，随t变化；Qi为对应于广义坐标qi的广义力。

联立上述各式，不设置线性弹簧[5]，仅考虑结构自定心刚度，可得悬吊结构体系非线性运动方程如下

(5)

由式(5)可知，地震作用下上部结构会存在一个摆角θ。随着摆角θ的增大，悬吊结构体系上部子结构将会形成一个较大的倾覆力矩，一旦倾覆力矩大于悬吊隔震支座极限承载能力，将会威胁到整个结构体系的安全。因此，通常情况下悬吊隔震支座摆角θ不应过大。在摆角θ较小的情况下，可将式(5)进一步等效线性化为以下形式

(6)

悬吊隔震层等效刚度k2为

(7)

以式(6)表示的悬吊结构体系等效线性运动方程为基础，对结构体系进行参数分析；以式(5)表示的悬吊结构体系非线性运动方程为基础，对结构体系进行时程响应分析，通过时程响应分析来验证等效线性化的正确性。

2 结构随机地震响应分析

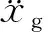
(8)

(9)

将表1中上下部子结构频率比f及外激励与下

表1 体系参数定义Tab.1 Definition of System Parameters

部子结构频率比λ代入式(8)，由此可得下部子结构与上部子结构的位移动力放大系数H1(iλ)，H2(iλ)分别为

(10)

(11)

(12)

(13)

3 悬吊隔震层优化设计

3.1 优化设计方法

由悬吊结构体系力学模型可知，地震作用下，上部子结构会存在一个摆角θ，由于摆角θ不能过大，即上部子结构相对位移x2有一定限制，因此提出一种综合考虑上下部子结构位移的优化方法。优化方法流程见图3，其中，α为性能目标函数中的参数，[x2]为隔震支座的水平位移限值。

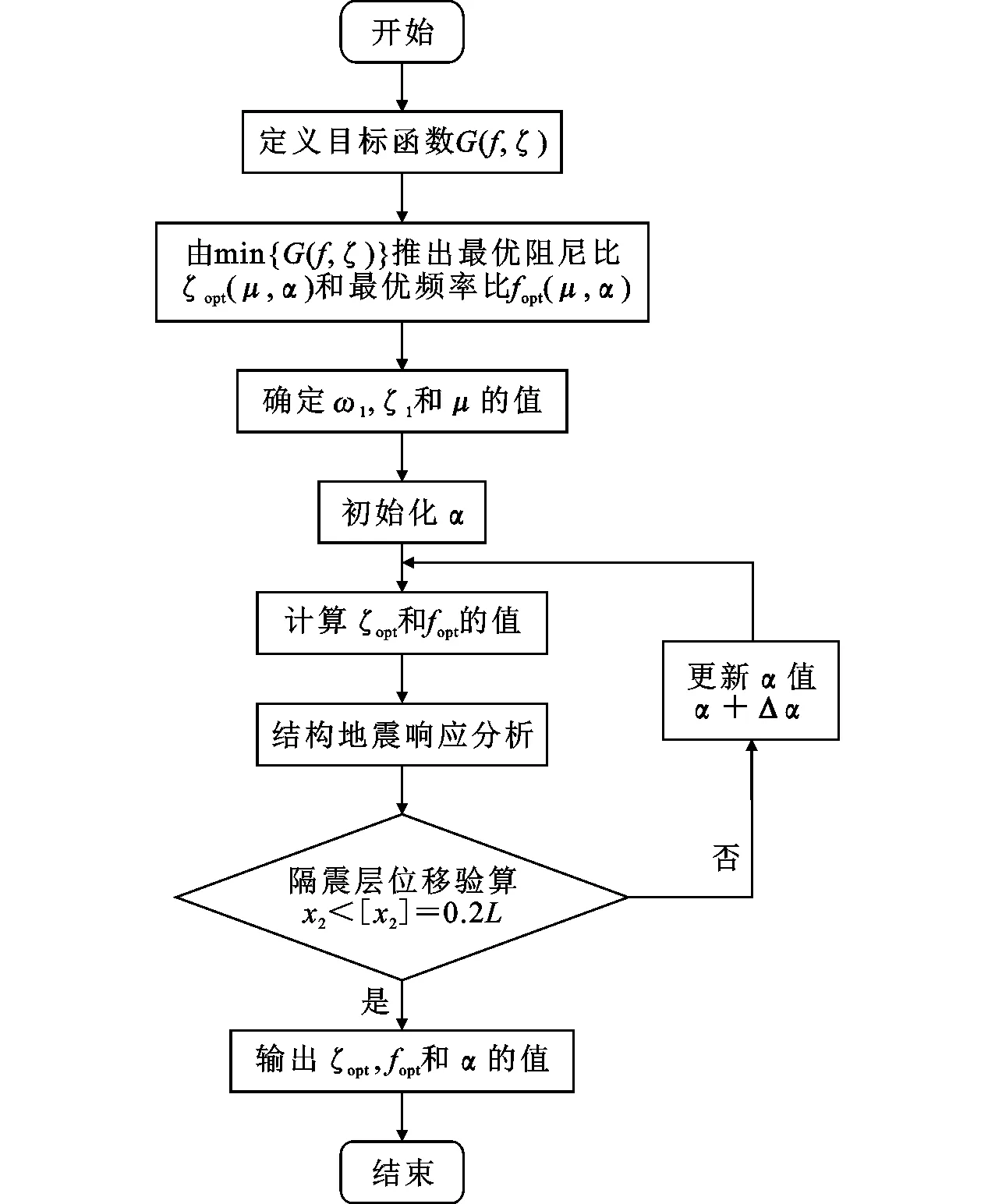
首先，综合考虑上下部子结构位移响应，定义含衡量悬吊结构体系上部子结构权重的性能指数α的性能目标函数，以性能目标函数最小为优化目标，推导悬吊结构体系最优频率比fopt与最优阻尼比ζopt的理论解。然后，初始化α，根据质量比及α的值，可计算悬吊层最优阻尼比ζopt及上下部结构最优频率比fopt，由此换算得到悬吊隔震层参数(摆长L与阻尼器阻尼系数c2)。对结构进行地震响应分析，并对上部子结构位移(或摆角)进行验算，满足要求则说明α取值合理，反之则增大α值进一步验算。通过上述过程，可使得隔震层位移满足要求的前提下，保证下部结构地震响应最小。

3.2 性能目标函数定义

本文在进行悬吊隔震层优化设计过程中，同时将下部子结构与上部子结构位移作为优化目标，综合考虑上下部子结构位移响应。事实上，根据工程实际情况确定隔震层位置之后，μ与ζ1等参数均已确定，悬吊隔震层优化设计本质上是计算上下部子结构频率比f与隔震层阻尼比ζ2的过程，由此可将层间悬吊隔震体系性能目标函数定义为

(14)

严格意义上来说，根据α的取值可将悬吊结构体系的减震目标划分为以下3个阶段：

(1)第1阶段：0<α<1时，悬吊结构体系主要用于控制下部子结构地震响应。

(2)第2阶段：α=1时，悬吊结构体系同时将上下部子结构地震响应作为控制目标，且上下部子结构重要性相同。

(3)第3阶段：α>1时，悬吊结构体系主要用于控制上部子结构地震响应。

总体来说，随着性能指数α的增大，上部子结构所占性能权重比增大，悬吊结构体系对上部子结构地震响应的控制力度也将加大，地震作用下，上部子结构位移响应相应减小更多。

3.3 最优设计参数理论解

为使层间悬吊隔震体系性能目标函数G(f,ζ2)最小，f与ζ2应满足以下条件

(15)

令下部子结构阻尼比ζ1=0，可进一步将式(15)整理为

(16)

(17)

(18)

联立式(16)～(18)可求得悬吊隔震层最优阻尼比为

(19)

(20)

(21)

(22)

(23)

同样可求得上下部子结构最优频率比为

(24)

(25)

3.4 参数分析

为了验证本文推导的悬吊隔震层最优阻尼比ζopt及上下部子结构最优频率比fopt理论解的正确性，有必要进行相应的系统参数分析。图4为性能指数α与质量比μ取不同值时，悬吊隔震层最优阻尼比ζopt及上下部子结构最优频率比fopt的理论解与数值解。其中，ζopt与fopt数值解的取值范围分别为[0，1.6]和[0，1]，计算步长均为0.01。从图4可以看出，ζopt与fopt的理论解和数值解基本吻合。

需要注意的是，ζopt数值解的计算精度通常会受参数取值范围与计算步长等因素的影响，因此ζopt数值解可能在局部区域内离散度较大。例如μ大于10时，ζopt数值解离散度较大，导致ζopt数值解与理论解之间存在较大的差别；计算fopt的最大相对误差为3.42%，ζopt的最大相对误差为4.72%，说明本文推导的ζopt与fopt理论解是正确的。由此可见本文推导ζopt与fopt理论解具有精度高、稳定性好等优点。从图4还可以观察到以下现象：

(1)随着性能指数α的增大，ζopt与fopt均会增大，结构体系所需的最优摆长减小。这是由于α的增大导致上部子结构所占性能权重比也随之增大，此时需要更大的隔震层刚度与阻尼系数来降低上部子结构的地震响应。

(2)最优阻尼比ζopt与质量比μ呈正相关关系；最优频率比fopt与质量比μ呈负相关关系。

(3)ζopt与fopt在质量比为1附近尤其是小于1时，斜率较大，说明质量比较小时，悬吊结构体系对阻尼比及频率比更为敏感。

4 算例验证及分析

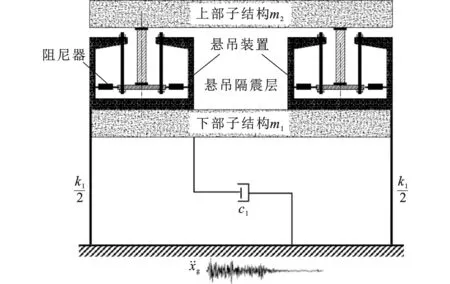
以某两层剪切型框架结构作为工程算例，对层间悬吊隔震体系减震性能进行数值分析。其中无悬吊隔震层的结构模型如图5所示；设置有悬吊隔震层的结构模型如图1所示(其中上部子结构简化为单层质量块)。结构第1层与第2层质量均为1×103t，刚度系数均为6.17×104kN·m-1，结构阻尼比取0.05。性能指数α分别为0.5，1，2，根据本文推导的理论公式，计算得到不同情况下的悬吊隔震层最优设计参数，如表2所示。

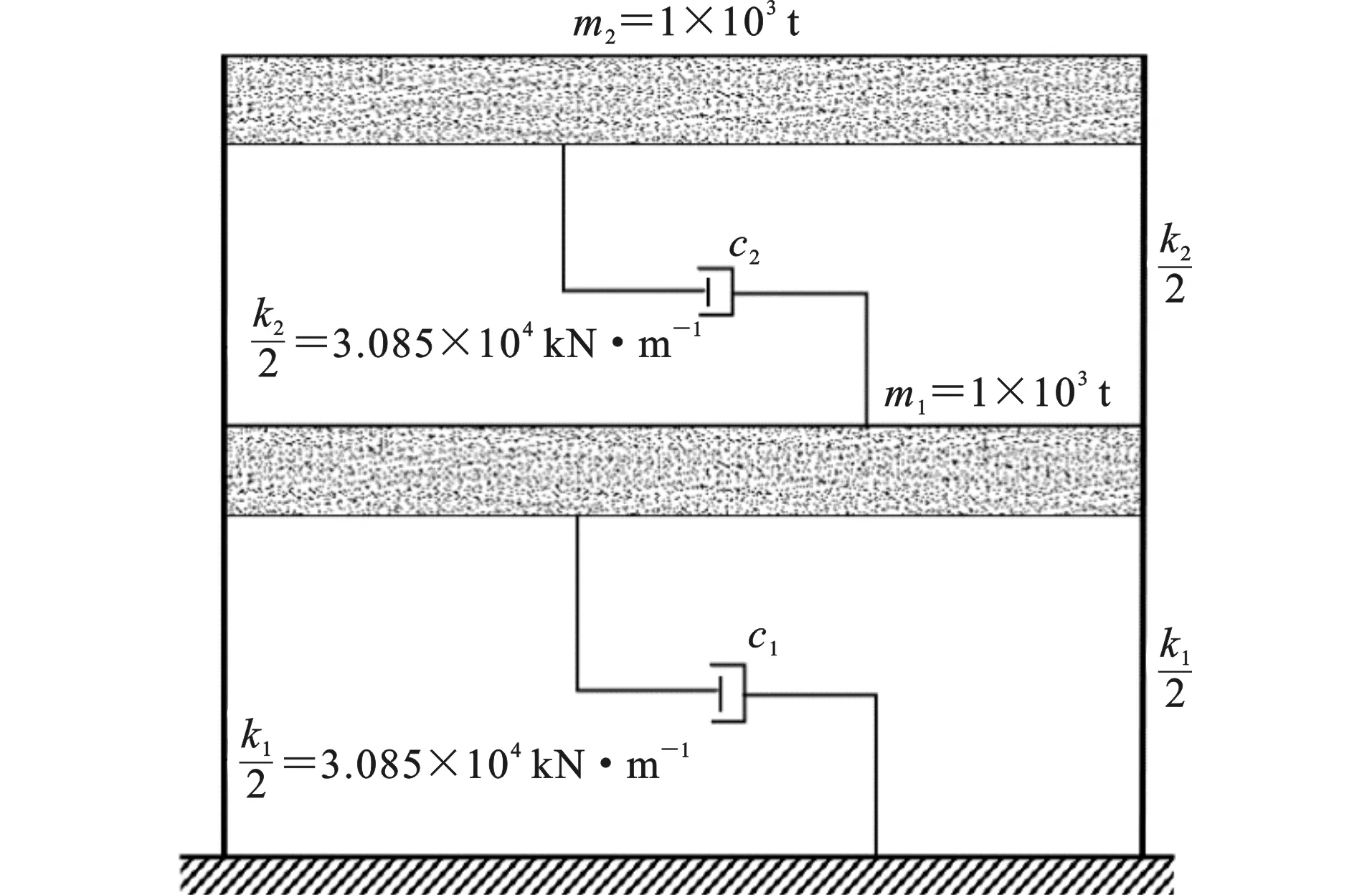
根据悬吊隔震层优化设计结果，对结构位移动力放大系数进行分析，结果如图6所示。从图6可以观察到，隔震结构上部子结构与下部子结构位移动力放大系数峰值均小于非隔震结构，说明悬吊隔震层位于层间能同时降低上部子结构与下部子结构

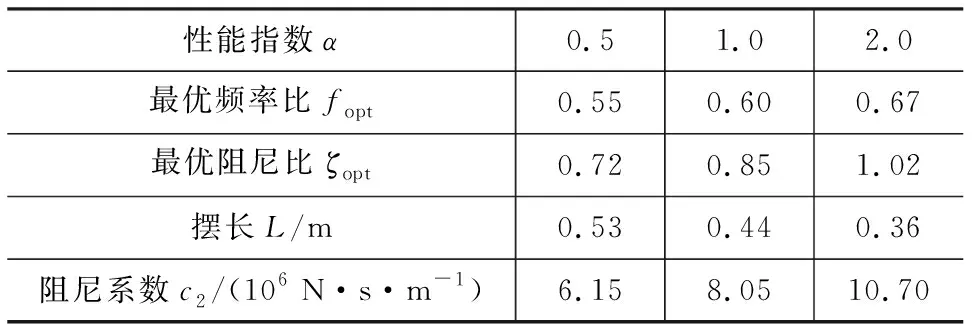
表2 悬吊隔震层优化设计结果Tab.2 Optimal Design Results of Suspension Isolation Layer

的位移响应峰值。值得一提的是，随着性能指数α的增大，下部子结构位移动力放大系数峰值会增大，而上部子结构位移动力放大系数峰值会减小，这一现象与α的定义是相符的。

为了对悬吊结构体系减震性能进行时程验证，以El Centro(EW,1940年)和Taft(EW,1952年)两组经典地震记录作为输入，并将地震记录幅值调整为70 cm·s-2。以式(5)表示的悬吊结构体系非线性运动方程为基础，基于MATLAB/Simulink平台使用Runge-Kutta法对体系进行时程响应分析。

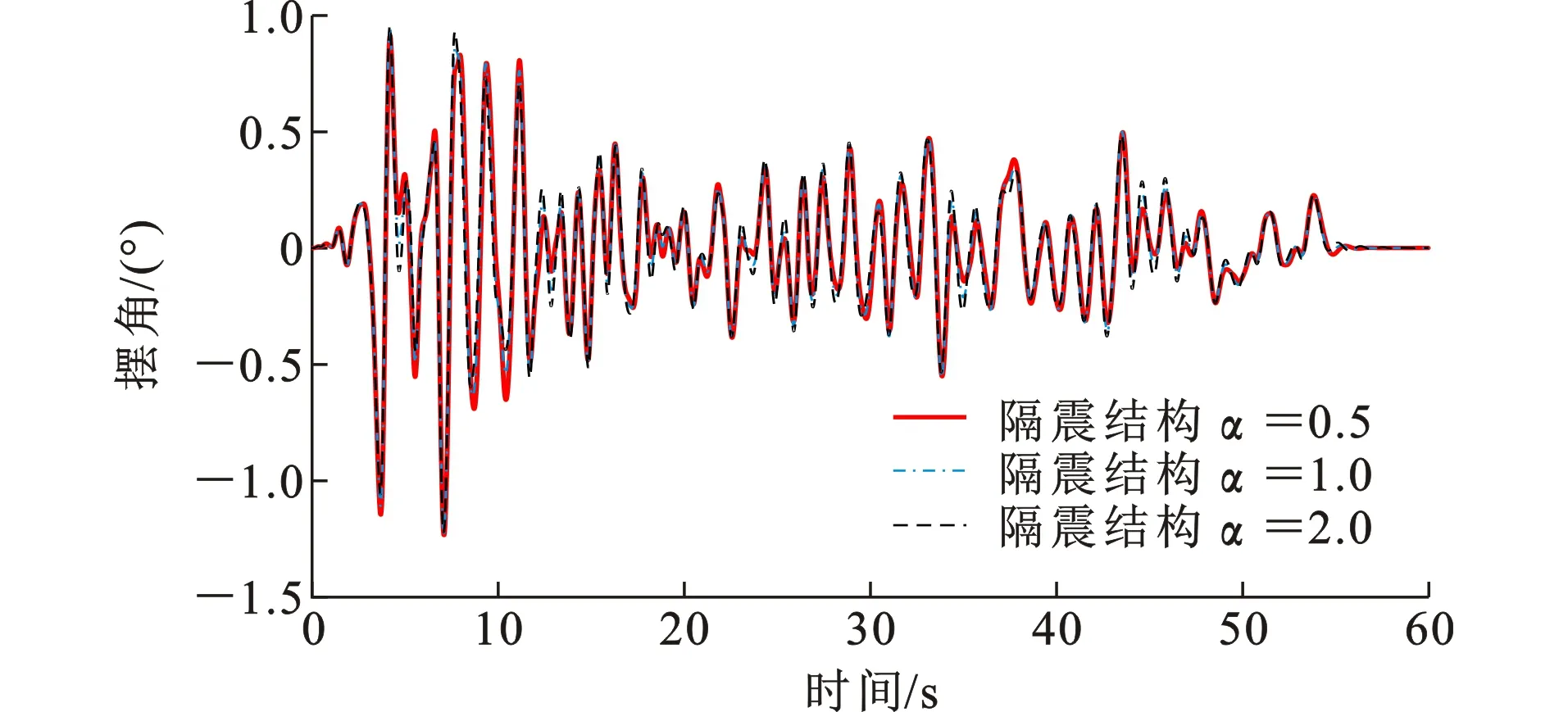
图7为El Centro地震作用下结构位移响应时程。从图7可以看出，结构响应均在0～15 s内占据一定的成分，随后逐渐衰减并在25 s后又出现一定成分，主要是由于El Centro地震记录在0～15 s初始阶段有相对较强烈的脉冲运动。相对于非隔震结构，悬吊结构体系的上部子结构与下部子结构地震位移响应明显减小。其中，上部子结构减震机理类似隔震，因此相对于下部子结构来说，位移减小更多；上部子结构位移满足小于0.2L的要求[4]，验证了等效线性化的正确性。图8为El Centro地震作用下结构悬吊隔震层摆角大小。从图8可以看出，采用层间悬吊结构体系进行优化设计后的结构，最大摆角不超过2.5°。

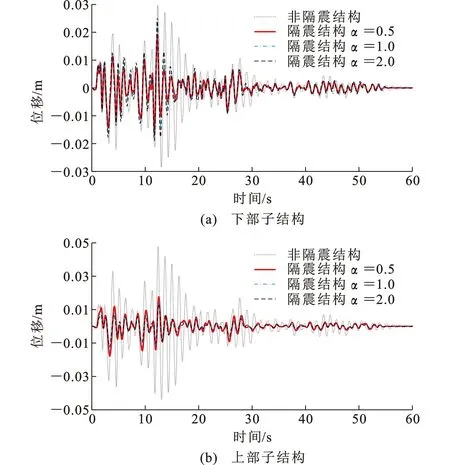
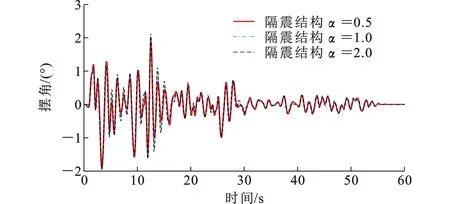
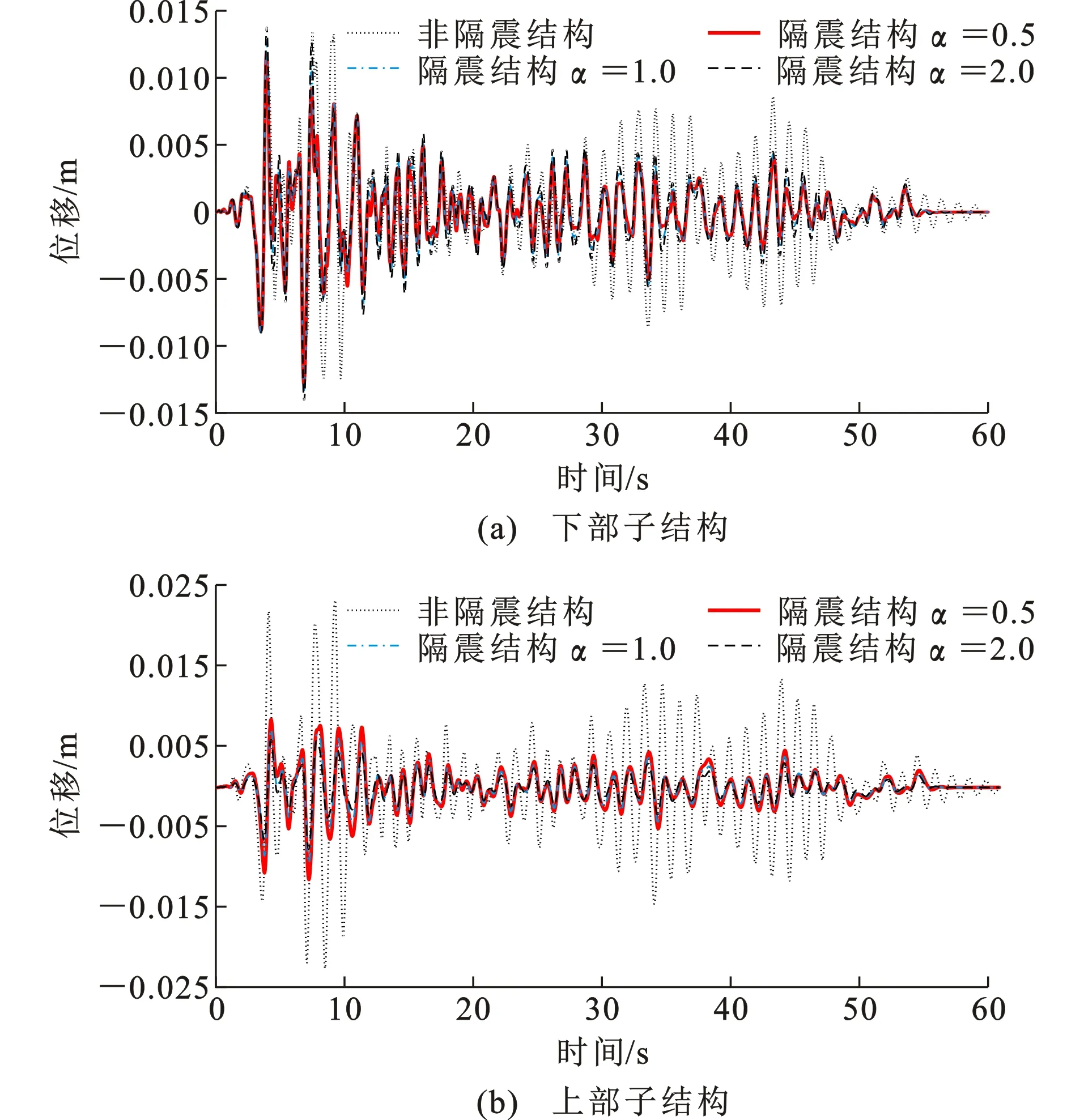
图9为Taft地震作用下结构位移响应时程。从图9可以看出，相对于非隔震结构，悬吊结构体系的上部子结构地震位移响应明显减小，下部子结构地震位移响应在地震动初始阶段减震效果不明显。隔震结构在0～8 s内位移响应相对于非隔震结构还略有增大，主要原因是上部子结构对下部子结构起到一定的调谐作用，其在地震刚发生的短时间内没有发挥，能量还来不及向上部转移；上部子结构位移满足小于0.2L的要求[4]，验证了等效线性化的正确性。图10为Taft地震作用下结构悬吊隔震层摆角大小。从图10可以看出，采用层间悬吊结构体系进行优化设计后的结构最大摆角不超过1°。

综上可知，悬吊隔震结构体系对于不同场地类型的地震记录均有一定的减震效果，且对于隔震层位于层间的悬吊隔震结构体系，上部子结构减震效果更好，并且可以通过改变性能指数α的值来调整上下部结构减震性能。

为了对悬吊结构体系减震性能进行定量分析，表3给出了性能指数α取不同值情况下的结构位移减震率(非隔震结构与隔震结构位移差值与非隔震结构位移的比值)，其中Taft地震记录下前期控制效果还未发挥段在计算峰值减震时不考虑。从表3

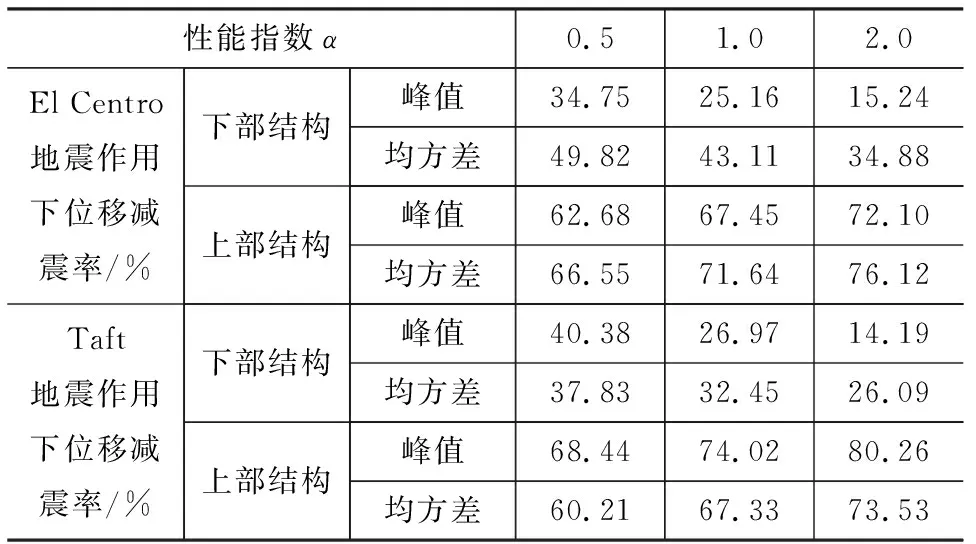
表3 地震作用下悬吊层间隔震体系位移减震率Tab.3 Displacement Attenuation Rate of Suspension Interlayer Isolation System Under Earthquakes

可以直观地看出，随着α的增大，悬吊隔震体系下部子结构位移响应峰值与均方差的减震率会下降，但是上部子结构位移响应峰值与均方差减震率略有上升。以结构位移响应峰值为例，α由0.5增加至2.0时，El Centro地震记录及Taft地震记录下悬吊隔震体系下部子结构位移减震率分别下降了19.51%和26.16%，而上部子结构位移减震率分别上升了9.52%和11.82%，可见上部子结构位移减震率的上升速度小于下部子结构位移减震率的下降速度。尽管α的增大会降低下部子结构的位移减震率，但是只要α取值合理，悬吊结构体系能同时有效控制上部子结构与下部子结构地震位移响应。以α=1.0为例，两地震作用下下部子结构位移响应峰值减震率分别为25.16%和26.97%，上部子结构位移响应峰值减震率高达67.45%和74.02%。

5 结 语

(1)提出了悬吊结构的优化设计方法，通过定义性能指数α，同时将悬吊结构的下部子结构与上部子结构反应作为优化目标，推导了悬吊隔震层最优设计参数理论解，参数分析结果表明，理论解具有精度高、稳定性好等优点。

(2)随着性能指数α的增大，上部子结构所占性能权重比增大，悬吊结构体系对上部子结构地震响应的控制力度也将加大。

(3)悬吊隔震层最优阻尼比ζopt与质量比μ呈正相关关系；上下部子结构最优频率比fopt与质量比μ呈负相关关系。ζopt与fopt在μ为1附近尤其是小于1时，斜率较大，变化较快，即此时悬吊结构体系对阻尼比及频率比更为敏感。

(4)通过算例分析可得，当性能指数α=1.0时，El Centro地震记录结构体系上下部子结构位移响应峰值减震率分别为67.45%和25.16%，Taft地震记录下结构体系上下部子结构位移响应峰值减震率分别为74.02%和26.97%。结果表明，悬吊隔震层位于层间的悬吊结构体系对于不同场地类型的地震记录下，均能同时有效控制上部子结构与下部子结构地震位移响应。