铝合金筋加固混凝土梁界面黏结性能与剥离承载力研究

2021-01-29邢国华罗小宝常召群党会学

建筑科学与工程学报 2021年1期

邢国华，罗小宝，马军，常召群，党会学

(长安大学建筑工程学院，陕西西安 710061)

0 引言

混凝土作为国内外使用最为广泛的建筑材料，在服役过程中会发生老化和病害。当混凝土构件不再满足承载力要求时，必须对其进行加固修复。嵌入式加固技术(Near Surface Mounted，NSM)作为一种新兴的加固方法，只需在既有构件表面制作凹槽，通过结构胶将加固筋嵌入凹槽并黏结以改善其力学性能。嵌入式加固技术较其他加固技术具有高强高效、耐腐蚀、抗冲击性强、耐久性和防火性优异等特点[1]。

国内外学者[2-3]采用纤维增强复合材料(Fiber Reinforced Polymer，FRP)对钢筋混凝土梁进行了嵌入式加固补强研究。结果表明，FRP作为加固材料可以提高混凝土梁的强度和刚度，但延性降低。铝合金筋作为一种新型的加固材料，具有比强度高、韧性好、质轻和耐腐蚀等优点。Rasheed等[4]和苟海刚等[5]采用铝合金筋作为加固筋改善了混凝土梁的变形性能和抗弯性能。加固筋-结构胶界面和结构胶-混凝土界面的黏结性能是影响加固筋与钢筋混凝土梁协同工作的关键因素，黏结-滑移本构模型是研究加固筋-结构胶和结构胶-混凝土界面黏结性能的重要依据之一[6]。文献[7]，[8]建立了加固筋与混凝土界面的黏结-滑移关系，但只研究了加固筋-混凝土界面的剪应力和滑移量，忽视了内嵌加固试件有3种介质(混凝土、结构胶和加固筋)和2个界面(加固筋-结构胶界面和结构胶-混凝土界面)，不能较好地描述加固筋-结构胶和结构胶-混凝土界面的受力特性。在实际工程中，剥离承载力指标对于界面性能评定更为直接，文献[9]～[13]基于试验研究和有限元模拟结果，提出了不同的剥离承载力计算模型。然而，目前有关混凝土梁黏结性能和剥离承载力研究中，加固筋多为FRP筋，采用铝合金筋加固混凝土梁的相关研究资料匮乏。因此，有必要对铝合金-结构胶和结构胶-混凝土界面黏结性能和剥离承载力进行分析研究。

本文以铝合金筋嵌入式加固混凝土梁为研究对象开展试验研究和有限元模拟，分析黏结破坏模式，探讨铝合金筋应力、黏结应力和滑移量沿梁跨度方向的分布情况，为研究铝合金筋嵌入式加固混凝土梁的黏结应力-滑移关系和剥离承载力计算模型提供参考。

1 试验概况

1.1 材料性能

试验选用强度等级为C40的商品混凝土，在试件浇筑过程中，预留边长为150 mm的混凝土立方体试块，并与试件在同等条件下养护，在试件加载时，依据《普通混凝土力学性能试验方法标准》(GB/T 50081—2002)[14]测得的混凝土立方体抗压强度为52.7 MPa。

纵筋和箍筋均为HRB400级钢筋，加固筋采用7075系高强铝合金筋，按照《金属材料拉伸试验第1部分：室温试验方法》(GB/T 228.1—2010)[15]进行性能测试，试验结果见表1。黏结材料为广州西卡建筑材料有限公司生产的Sikadur 330CN/30CN双组分环氧树脂型结构胶，其性能参数见表2。

1.2 试件设计

试验共制作了4根钢筋混凝土梁，截面高度为300 mm，宽度为170 mm或240 mm，梁长为3 000mm，净跨为2 800 mm，剪跨比为3.7，顶部及侧面的保护层厚度为20 mm，底部的保护层厚度为30 mm，配筋详情及尺寸参数见图1和表3，P为荷载。

表1 钢筋和铝合金筋的性能参数Tab.1 Performance Parameters of Steel Bars and AA Bars

表2 Sikadur 330CN/30CN结构胶力学性能参数Tab.2 Performance Parameters of Sikadur 330CN/30CN Structural Adhesive

加固梁采用近表面嵌入式加固技术，根据设计规范ACI 440-08[16]，试件制作时预留截面尺寸为25 mm×25 mm的凹槽，将凹槽清理干净后，用黏结剂将凹槽填充至一半，将铝合金筋压入凹槽内，再用黏结剂填满凹槽，最后用刮刀压实并抹平。

表3 试件设计参数Tab.3 Design Parameters of Specimens

1.3 加载方案

试验采用两点对称加载方式，纯弯段和弯剪段长度分别为600 mm和1 100 mm。荷载P由50 t液压千斤顶通过分配梁提供2个对称的集中荷载，千斤顶与分配梁之间放置球铰支座以确保荷载均匀施加，加载速率为0.6 mm·min-1。分别在加载点和跨中布置竖向位移计，试验梁内部钢筋和铝合金筋表面均粘贴应变片，测点位移和钢筋应变通过采集仪记录。

2 试验结果及分析

2.1 试验现象

试验梁破坏形态见图2，对比梁RCB发生了典型的弯曲破坏。加载初期，试件的荷载-挠度呈线性变化，荷载加至20.1 kN时，试验梁跨中位置出现一条弯曲裂缝。随荷载增加，弯剪段和纯弯段不断出现新裂缝，已有裂缝向上延伸且宽度增大。荷载加至66.9 kN时，受拉钢筋屈服，此时纯弯段不再产生新的裂缝。荷载加至71.8 kN时，纯弯段裂缝进入不稳定发展阶段，宽度急剧增加，弯剪段裂缝基本不再延伸；荷载达到80 kN时，梁跨中受压区混凝土开始起皮。当跨中挠度达到58.7 mm时，跨中混凝土保护层压溃剥落，荷载由81.7 kN突降至60 kN，试验梁破坏。

试件BA-E-1发生了界面剥离破坏，试件BA-E-2和BA-E-3发生了混凝土保护层剥离破坏，破坏过程相似，故仅对试件BA-E-1的破坏过程进行描述。荷载加至27.2 kN时，梁纯弯段底部出现1条可见裂缝，此时跨中挠度为2.0 mm。加载至55.2 kN时，梁纯弯段及弯剪段底部混凝土出现多条裂缝，并沿垂直于胶槽方向发展。荷载加至77.1 kN时，受拉钢筋屈服；荷载加至85.7 kN时，伴随着“砰”的声响，梁跨中底部胶槽与周围混凝土开裂，此时跨中挠度为14.6 mm。加载至110.1 kN时，试验梁达到极限承载力，此时跨中挠度为32.2 mm。随荷载继续增加，梁端支座处底部出现顺槽裂缝且不断延伸。当位移达到32.3 mm时，伴随着连续的“噼啪”声响，顺槽裂缝占据整个胶槽长度，加固梁试件发生大范围混凝土保护层剥离，荷载由110.1 kN突降至57.9 kN，试件破坏。

2.2 荷载-挠度曲线

图3为各试验梁的荷载-挠度曲线。表4为主要试验结果。图3中可将试验梁的破坏过程分为3个阶段：弹性阶段、混凝土开裂至钢筋屈服阶段和钢筋屈服至试件破坏阶段。从图3可以看出，弹性阶段时，加固梁荷载-挠度曲线的斜率大于对比梁，说明加固筋的存在增加了梁的刚度。由表4可以看出，对比梁的延性优于加固梁。另外，通过荷载-挠度曲线可以看出，加固梁在破坏后，仍然具有一定的承载能力，虽然荷载在试验梁破坏时发生了突降，但随着位移的增加，荷载仍然有增加的趋势，其原因在于，铝合金筋具有较高的延性，在梁存在较大变形的情况下仍然具有一定的承载能力。

3 有限元分析

3.1 模型建立

试验梁有限元模型如图4所示，根据对称性，选取试验梁1/4结构作为研究对象，在对称面施加对溃破坏，IC表示界面剥离破坏，CCS表示混凝土保护层剥落破坏。

表4 主要试验结果Tab.4 Main Test Results

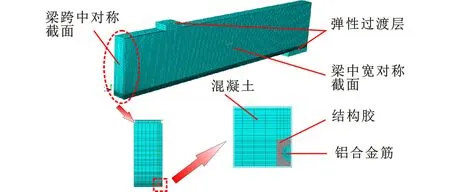
混凝土材料、结构胶、铝合金筋和弹性过渡层选用C3D8R单元模型，钢筋选用T3D2单元模型，其中，过渡层为线弹性材料，弹性模量为3.05×105MPa，泊松比为0.3。根据《混凝土结构设计规范》(GB 50010—2010)[19]，混凝土选用ABAQUS内置的塑性损伤模型，钢筋采用双线性弹塑性强化模型，铝合金筋采用双线性弹塑性强化模型，钢筋的本构关系为

(1)

式中：σ为钢筋应力；ε为钢筋应变；fy为钢筋受拉屈服应力；Es为钢筋弹性模量；εy为钢筋屈服时对应的应变；εu为钢筋极限应变。

铝合金筋采用双线性弹塑性强化模型，应力-应变关系表达式如下

(2)

式中：fa为铝合金筋应力；εa为铝合金筋应变；f0.2为铝合金筋受拉屈服应力；Ea为铝合金筋弹性模量；ε0.2为铝合金筋屈服时对应的应变。

3.2 模型验证

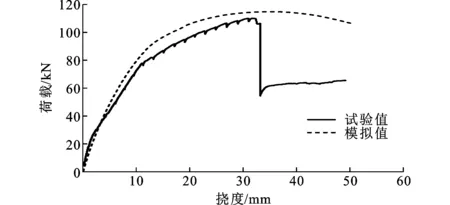
图5和图6分别给出了梁BA-E-1的荷载-挠度曲线和铝合金筋应变分布规律的有限元分析结果和试验结果对比情况。由图5可见：在试件发生剥离破坏前，模拟曲线与试验曲线发展趋势基本相同，各受力阶段曲线吻合较好；达到峰值点时试件发生界面剥离破坏，试验曲线陡降，而模拟曲线下降缓慢。由图6可知：铝合金筋应变分布曲线与试验曲线吻合较好，当P/PIC≤0.6(PIC为试件BA-E-1剥离荷载的有限元模拟值)时，铝合金筋应变沿梁长度方向波动较小；当P/PIC>0.6时，在加载点梁底部附近，铝合金筋应变出现明显波动，该现象与混凝土开裂有关。因此，建立的有限元模型可以较好地模拟铝合金筋加固混凝土梁的受力性能。

3.3 界面剥离破坏过程模拟

图7为梁BA-E-1的荷载-挠度计算曲线模拟结果，并选取加载过程中的5个特征点，记为A～E，分别对应20%PIC，40%PIC，60%PIC，80%PIC和100%PIC。图8给出了梁BA-E-1的裂缝发展云图。

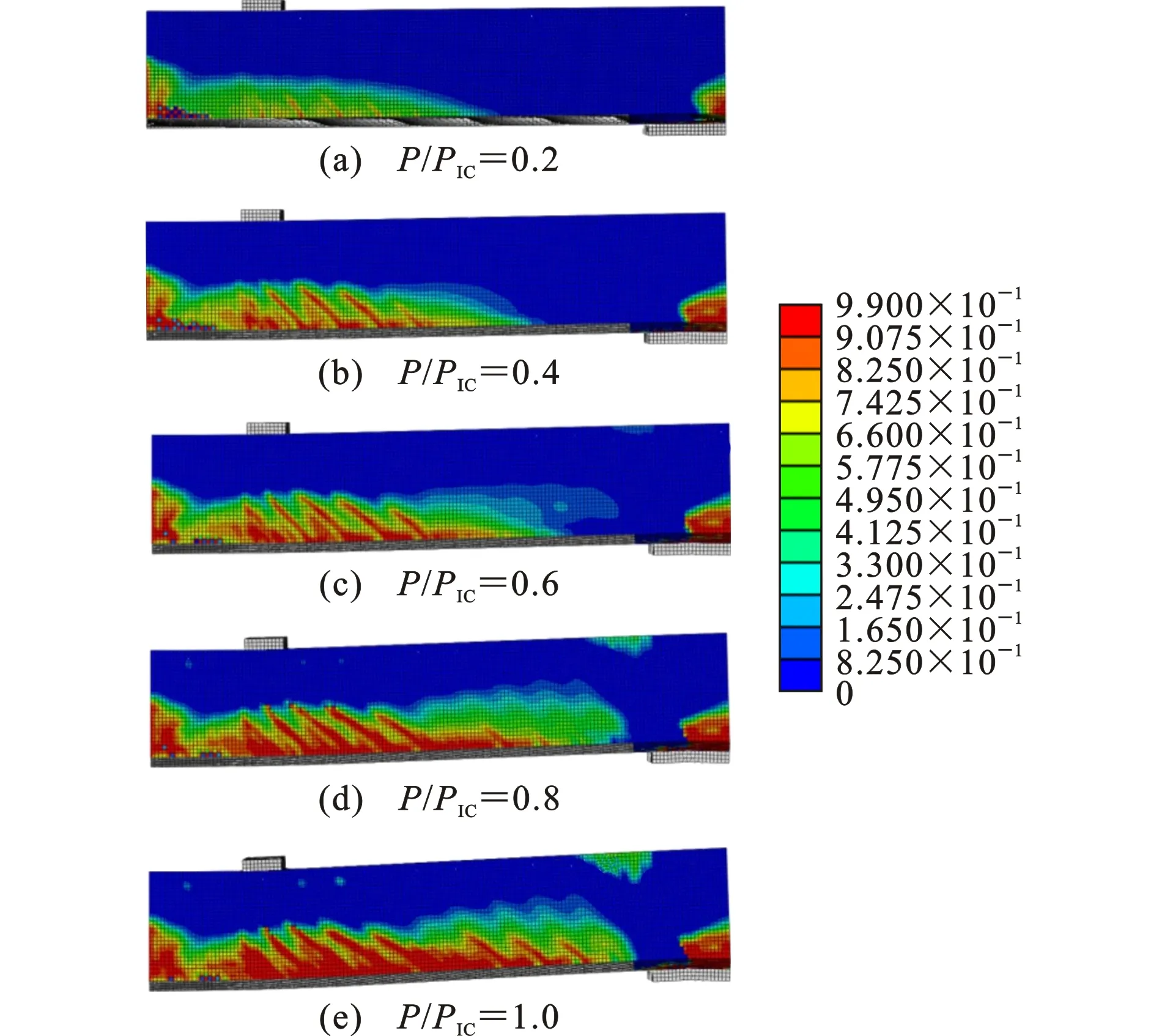
由各特征点对应的混凝土开裂云图可以看出，裂缝形式主要分为3类：弯曲裂缝、斜裂缝和微裂缝。弯曲裂缝出现在梁的弯曲段，裂缝分布相对均匀，主要是由混凝土受拉开裂引起；斜裂缝出现在梁的弯剪段，主要由试件在加载过程中出现的剪切变形引起；微裂缝区为图8中裂缝发展云图的白色区域，随荷载增加，逐渐转变为主要裂缝。最终，界面剥离先在加载点梁底部出现，与试验现象一致。

3.4 界面黏结应力-滑移模型

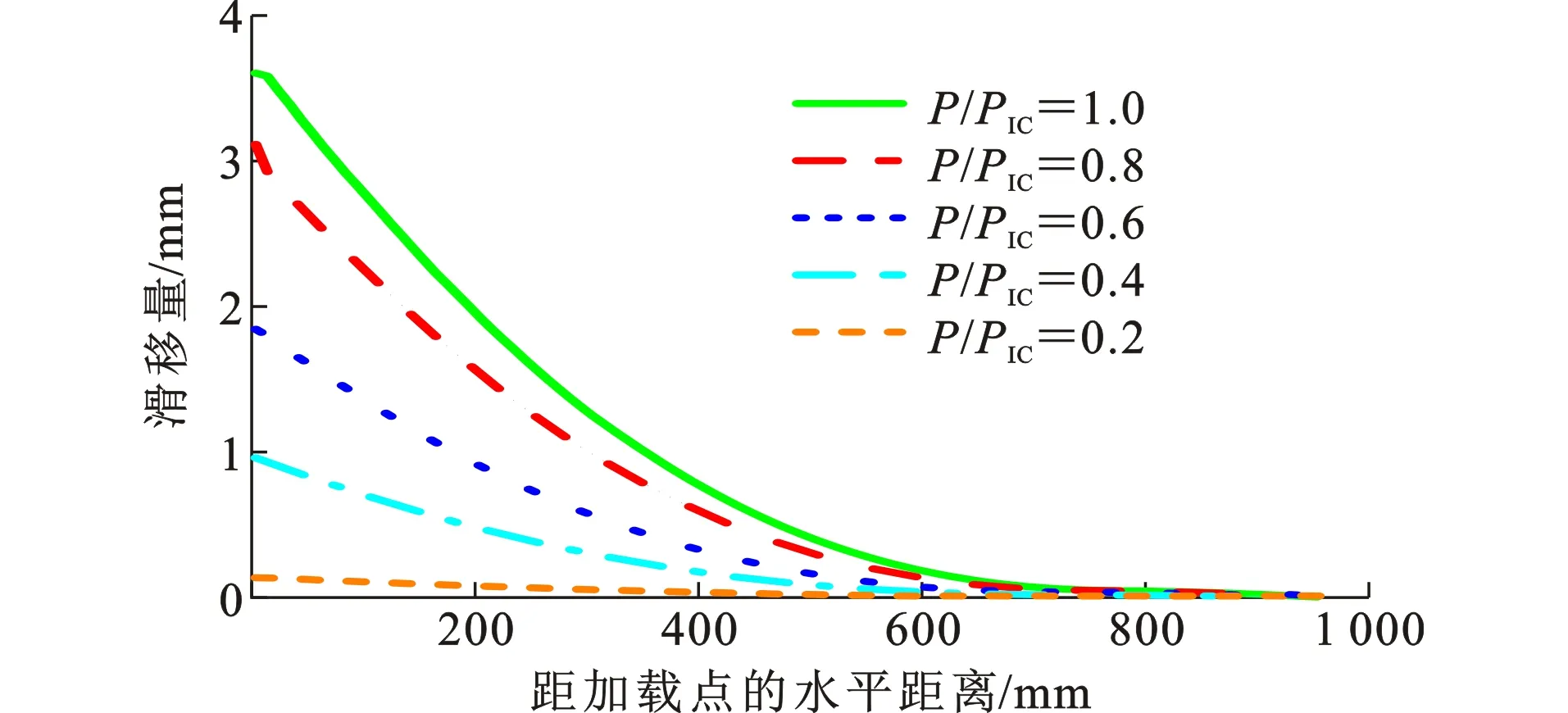
图9反映了铝合金-混凝土界面相对滑移规律，铝合金-混凝土界面相对滑移随荷载级别增加而增加，沿铝合金筋黏结长度方向，滑移量逐渐降低，加固筋端部滑移量几乎为0，可以忽略不计。

通过模拟得到铝合金筋的应力分布(图10)，利用差分计算得到界面黏结应力[20]分布曲线(图11)。由图10可知：铝合金筋应力分布沿梁跨度方向逐渐降低，当荷载较小时，试验梁底部的裂缝分布相对均匀，此时铝合金筋的应力沿梁跨度方向分布比较光滑，在裂缝区段内铝合金筋的应力有细微波动，其大小随荷载增加而增加，铝合金-混凝土界面产生相对滑移；临近剥离破坏时，加载点梁底部附近铝合金筋应力产生了较为明显的波动，由界面剥离裂缝随机扩展所致。

图11可以直观地反映出试验梁界面剥离过程中各界面的力学行为，其发展特征如下：①荷载达到20%PIC时，黏结应力主要集中在加载点梁底部附近，沿铝合金筋黏结长度方向黏结应力逐渐降低；②荷载位于40%PIC和60%PIC之间时，梁底部加载点附近处于复合应力作用区域，裂缝发展迅速，率先达到黏结应力最大值，界面开始出现损伤，黏结应力沿梁跨度方向呈现出明显的波浪状分布规律；③荷载达到80%PIC时，由于加载点梁底部附近产生了多条主裂缝，混凝土对铝合金筋的约束作用较其他位置弱，黏结应力分布较为复杂，出现正负号交错的现象，混凝土开裂比较严重；④荷载达到100%PIC时，加载点梁底部附近混凝土完全剥离，黏结应力接近0 MPa，梁底部形成了1条明显的剥离裂缝。

3.4.1 铝合金-结构胶界面黏结应力-滑移模型

远离加载点的梁底部区域无法得到黏结应力-滑移曲线的“下降段”和“趋向水平区段”，这是因为试件破坏时，该区域内界面未完全剥离[21]。在距加载点梁底部170 mm位置处对数据进行提取，得到了铝合金-结构胶界面黏结应力-滑移曲线，如图12所示。

由图12可知，铝合金筋加固混凝土梁在加载过程中的剥离破坏过程分为4个阶段：①弹性阶段，黏结应力随滑移量的增加呈线性增加，界面3种介质(混凝土、结构胶和铝合金筋)变形协同；②弹性软化阶段，界面处裂缝不断发展，宽度不断增大，刚度不断降低，黏结应力增长缓慢；③弹性软化剥离阶段，界面开始剥离，黏结应力随着滑移量的增加而减小；④软化剥离阶段，界面完全剥离，试件破坏。

已有研究表明[22]，基于BPE模型建立与试验数据或有限元分析结果吻合较好的MBPE模型，计算公式为

(3)

式中：τ为局部黏结应力；s为滑移量；τmax为极限黏结应力；s0为极限黏结应力对应的滑移量；β和α为回归系数；k为软化刚度系数。

采用MBPE模型对铝合金-结构胶界面黏结应力-滑移曲线进行数值拟合，拟合结果如图13所示，拟合系数见表5。

3.4.2 结构胶-混凝土界面黏结应力-滑移模型

本节对结构胶-混凝土界面的力学行为进行了研究，铝合金筋微元的受力状态和复合体微元的受力状态如图14所示，其中，τ1为加固筋-结构胶界面剪应力，τ2为结构胶-混凝土界面剪应力，df为铝合金筋直径，σf为铝合金筋的拉应力。

表5 黏结应力-滑移曲线参数拟合值Tab.5 Fitting Values of Bond Stress-slip Curve Parameters

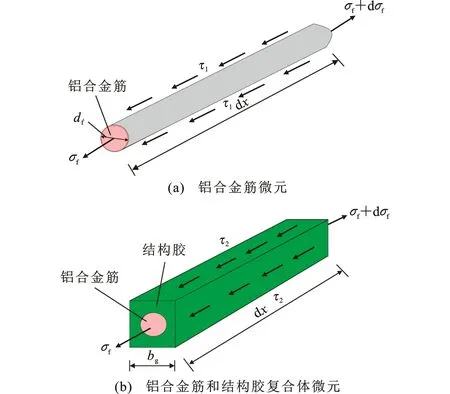
截取铝合金筋微元体进行分析，将加载端定义为x轴起点，加载端至梁端方向定义为x轴正向，通过对微元体的受力分析可以得出静力平衡方程[20]，即

(4)

式中：σf为铝合金筋轴向应力；Lper为破坏面的周长，当破坏发生在混凝土-胶层界面时，Lper=3bg，bg为方形槽的边长；当破坏发生在铝合金-胶层界面时，则有Lper=πdf；Af为铝合金筋的截面面积。

在加载过程中，假定铝合金筋微元与复合体微元受力相等，通过铝合金-结构胶界面和结构胶-混凝土界面上力的平衡关系可得

τ1πdfdx=Afdσf

(5)

3τ2bgdx=Afdσf

(6)

由式(5)和式(6)得

τ2=0.67τ1

(7)

根据式(3)和式(7)可得到结构胶-混凝土界面黏结应力-滑移曲线，通过MBPE模型对结构胶-混凝土界面黏结应力-滑移曲线进行数值拟合，拟合曲线如图15所示，拟合系数见表6。

表6 黏结应力-滑移曲线参数拟合值Tab.6 Parameter Fitting Values of Bond Stress-slip Curve

4 剥离承载力

黏结应力-滑移曲线所围成的面积为界面剥离断裂能Gf，剥离承载力主要取决于界面剥离断裂能[23]。本文选用了7个剥离承载力计算模型，对铝合金筋嵌入式加固梁进行计算分析，计算结果如表7所示。

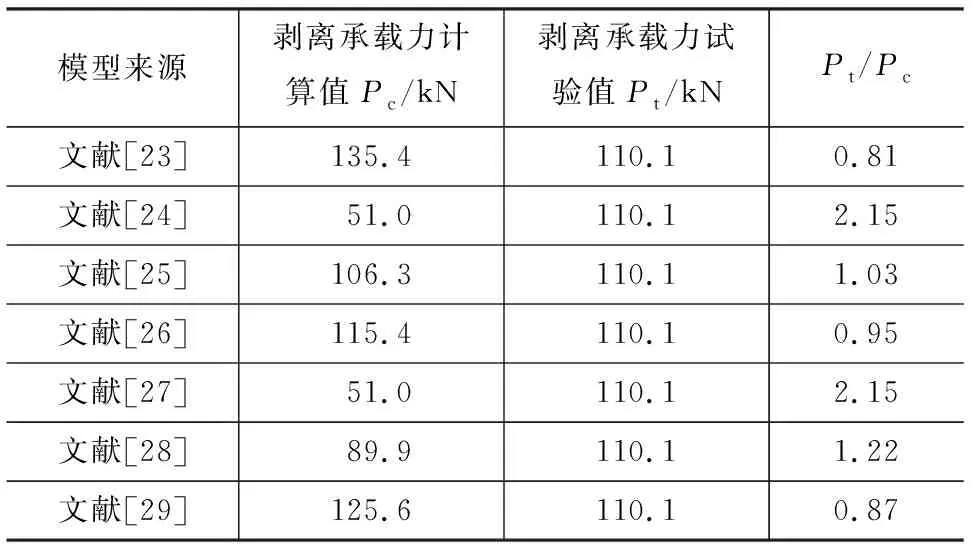
表7 剥离承载力计算结果Tab.7 Calculated Results of Debonding Capacity

从表7可以看出：文献[23]、文献[26]和文献[29]模型的计算值高于试验值，是因为这3种模型是基于面内剪切试验提出的，加固筋受力方向与加固筋-混凝土界面方向平行，界面受力方式为纯剪切，对于铝合金筋加固混凝土梁剥离承载力的预测存在偏差；文献[24]、文献[27]和文献[28]模型的计算值低于试验值，表明这3种模型偏于保守，考虑影响黏结性能的因素较少，仅表示为黏结区域内的几何特征函数；文献[25]模型考虑了多种影响黏结性能的因素(有效黏结长度、加固筋的刚度和混凝土的强度等)，可以比较准确地预测铝合金筋加固混凝土梁的剥离承载力。在文献[25]模型基础上，结合有限元模型得到的铝合金-结构胶界面和结构胶-混凝土界面的黏结应力-滑移曲线，分别建立界面发生剥离破坏时的剥离承载力计算公式，即

(8)

(9)

式中：Ef为铝合金筋弹性模量；Af为铝合金筋截面面积。

由于试验数据有限，采用本文试件BA-E-2和BA-E-3对剥离承载力计算公式(8)，(9)进行验证，结果见表8。

表8 剥离承载力试验值与计算值对比Tab.8 Comparison Between Test Values and Calculation Values of Debonding Capacity

由表8可知，试件BA-E-2，BA-E-3的剥离承载力试验值与计算值的比值分别为1.01和0.95，吻合较好。本文提出的剥离承载力计算公式是基于试验结果和有限元分析得到的，能反映出铝合金筋加固混凝土梁的真实受力状态，该剥离承载力计算模型有如下优点：①适用于铝合金嵌入式加固钢筋混凝土梁界面剥离承载力的计算，且计算简便；②根据铝合金筋嵌入式加固钢筋混凝土梁的基本参数和破坏模式，可以准确计算界面剥离承载力。