基于口令的密钥提取
2021-01-29刘迎风刘胜利
刘迎风,刘胜利
(1.上海市大数据中心,上海 200072;2.密码科学技术国家重点实验室,北京市5159信箱,100878 3. 上海交通大学 计算机科学与工程系,上海 200240 4.成都卫士通信息产业股份有限公司 摩石实验室,北京 100070)
基于口令认证系统[1-2]一般都使用用户名和口令对用户进行鉴别,这也是目前最广泛的身份认证方式。各大网站、银行系统、邮件系统、电脑登录等都使用了这种方法。目前基于口令的认证系统大都使用以下两种方法。第一种方法是认证服务器将“(用户名,口令)”存入数据库。认证时,用户从客户端输入自己的用户名和口令,用户名和口令经网络传输后,服务器对数据库寻找“(用户名,口令)”进行匹配。如果匹配成功,则认证通过;否则,认证失败。这种方法将各个用户的口令以明文方式存储在数据库中,大大增加了口令被窃的风险。例如,黑客入侵网站并获取网站数据库中的数据,或者内部管理人员窃取网站数据库的数据,就可以从数据库中直接获得口令。目前已有来自RockYou、MySpace、CSDN、天涯、DuDuNiu等共两百多个网站的用户和口令信息在网上被传播和贩卖。第二种方法则是对用户口令的哈希加盐,也就是口令后面加一段随机值(salt),然后进行哈希运算,得到加盐哈希值。认证服务器将“(用户名,盐,加盐Hash值)”存入数据库。认证时,只需计算用户口令的加盐哈希值,并判断与库中的值是否一致即可。
口令的优缺点相辅相成。其优点是:容易记忆;缺点是:作为随机变量,其概率分布不均,故熵值不高。WANG等人[3-4]对中国网站用户所调的口令的特点进行了分析,发现用户更喜欢使用人名、生日及与自己相关的一些信息作为口令。虽然目前已经存在并实现了比较好的基于口令的认证手段,但是,口令因其自身“易记低熵”的特性,很难将其用于加密等更复杂的密码系统中。正是因为这个特点,目前关于口令的更多应用是将口令作为一个因子进行双因子或者多因子认证[2,5-6]。
目前,我国已经制定了中国的国密标准算法系列(如SM1、SM2、SM3、SM4、SM7、SM9、ZUC算法)。这些密码算法绝大多数都需要密钥的参与。有了密钥,密码算法就可以实现丰富的密码功能,保障信息安全。而密码算法实现安全的必要条件是:密钥均匀随机。
口令“易记低熵”,可以做认证,但是不能实现加密等其它的密码功能。而密码算法虽然可以提供丰富的密码功能,却需要一个均匀随机的密钥做支撑。一个自然的想法是:“能否将口令结合到密码系统中去?”
口令是个人主观设定并记忆的,随机性不高,不符合密钥的要求。显然,不能直接将口令用作密钥。如果能够将口令转换成密钥,那么就可以使用口令来调用密码算法了。问题是:“如何将口令转换成均匀随机的密钥呢?”
文中的研究目的是回答上述两个问题,提出将口令转换成均匀随机的密钥的技术,将口令结合到密码系统中去,进而实现更加灵活丰富的密码功能。
1 基本概念及基础知识
统计距离是一种用来衡量两个随机变量的概率分布的相似性的标尺,两个随机变量的统计距离越小,这两个随机变量的概率分布就越相近。下面是统计距离的正式定义。
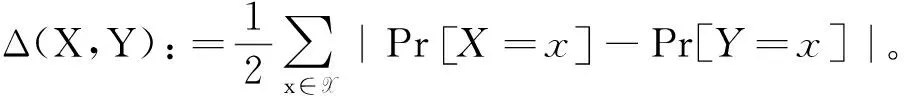
定义2【最小熵】对于集合X上的随机变量X,定义H为X的最小熵,熵的单位是bit。
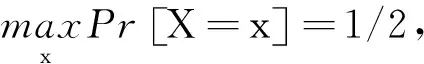
定义3【通用哈希(Universal Hash)函数】[7]设H: X→Y是一个函数族。如果对于所有的x≠x′∈X,Pr[H←H:H(x)=H(x′)]≤ 1/|Y|,那么H是一个通用哈希(Universal Hash)函数族。
定义4【Toeplitz矩阵】[8]如果矩阵(可以不是方阵)中每条自左上至右下的45°斜线上的元素都相同,那么称这个矩阵为Toeplitz矩阵。
引理1【剩余哈希引理(Leftover Hash Lemma)】[9]H={H:X→Y }是一个通用哈希(Universal Hash)函数族。对于集合X上的随机变量X,只要满足H(X)≥k,都有
(1)
其中,H为H中均匀随机选取的哈希函数,Uy为集合Y上的均匀分布。
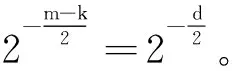
2 基于口令的密钥提取方案
首先对大量的口令进行统计分析,探询其统计规律。针对其统计特性,提出基于口令的密钥提取方案。在基于口令的密钥提取方案中,首先利用口令的统计特性估计“口令的熵值”,再根据熵值选择“Toeplitz矩阵”。使用Toeplitz矩阵对口令进行压缩以提取密钥。所提取的密钥可以应用于不同的密码系统中以实现认证或者加密。最后,建议通过“标准的密钥扩展函数”,对密钥进行扩展,这样就可以从一个口令推得多个密钥,应用于多个不同的密钥系统中。下面将分三小节描述:2.1节中介绍如何对口令库进行统计分析;2.2节中介绍提出的基于口令的密钥提取方案,将详细描述方案的各个模块,以及各个模块之间的联系;2.3节中解释密钥提取的原理。
2.1 口令库的统计分析
从网络上收集到了DuDuNiu网站的公开口令库,从中选取 200 000 条口令进行简单的分析。图1为 200 000 条口令中使用频率最高的14个口令。从图1中可以看出,用户使用最多的口令多为字母、数字的简单组合,如口令q123456出现了 1 890 次、口令a123456出现了988次、口令123456出现了978次。这种简单的口令固然降低了用户的记忆难度,但是其概率分布极不均匀。另一方面,一个均匀随机的口令看上去往往是无意义的、很难以被记忆的,用户很难直接对一个均匀随机的密钥进行记忆。

图1 DuDuNiu网站最常用口令分布
希望能够找到一种方法:可以从口令中获取均匀随机的密钥,这样既避免了增加用户的记忆负担,又可以使用所获得的密钥实现密码功能。
2.2 基于口令的密钥提取方案
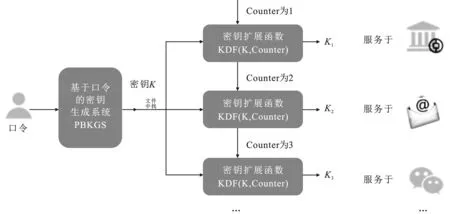
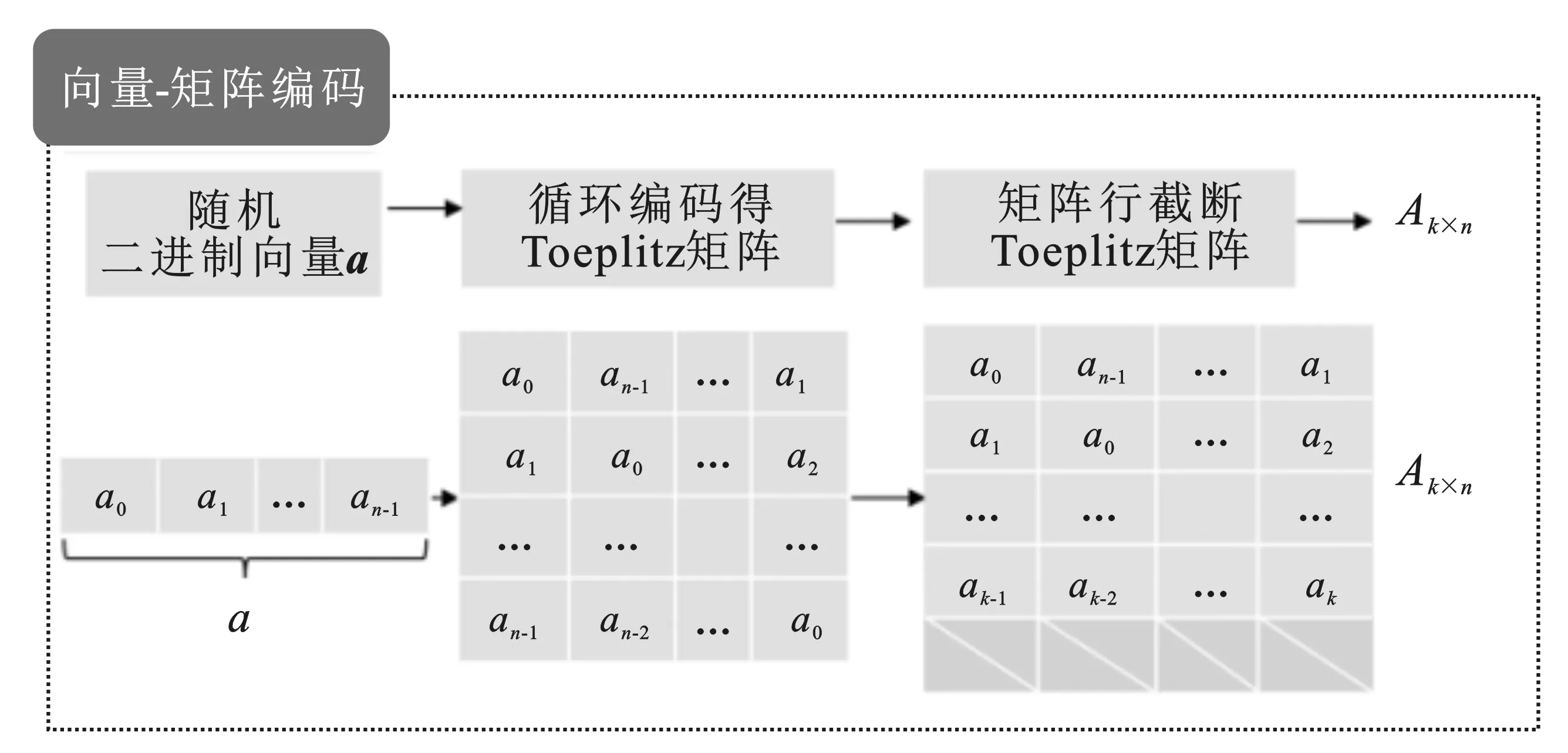
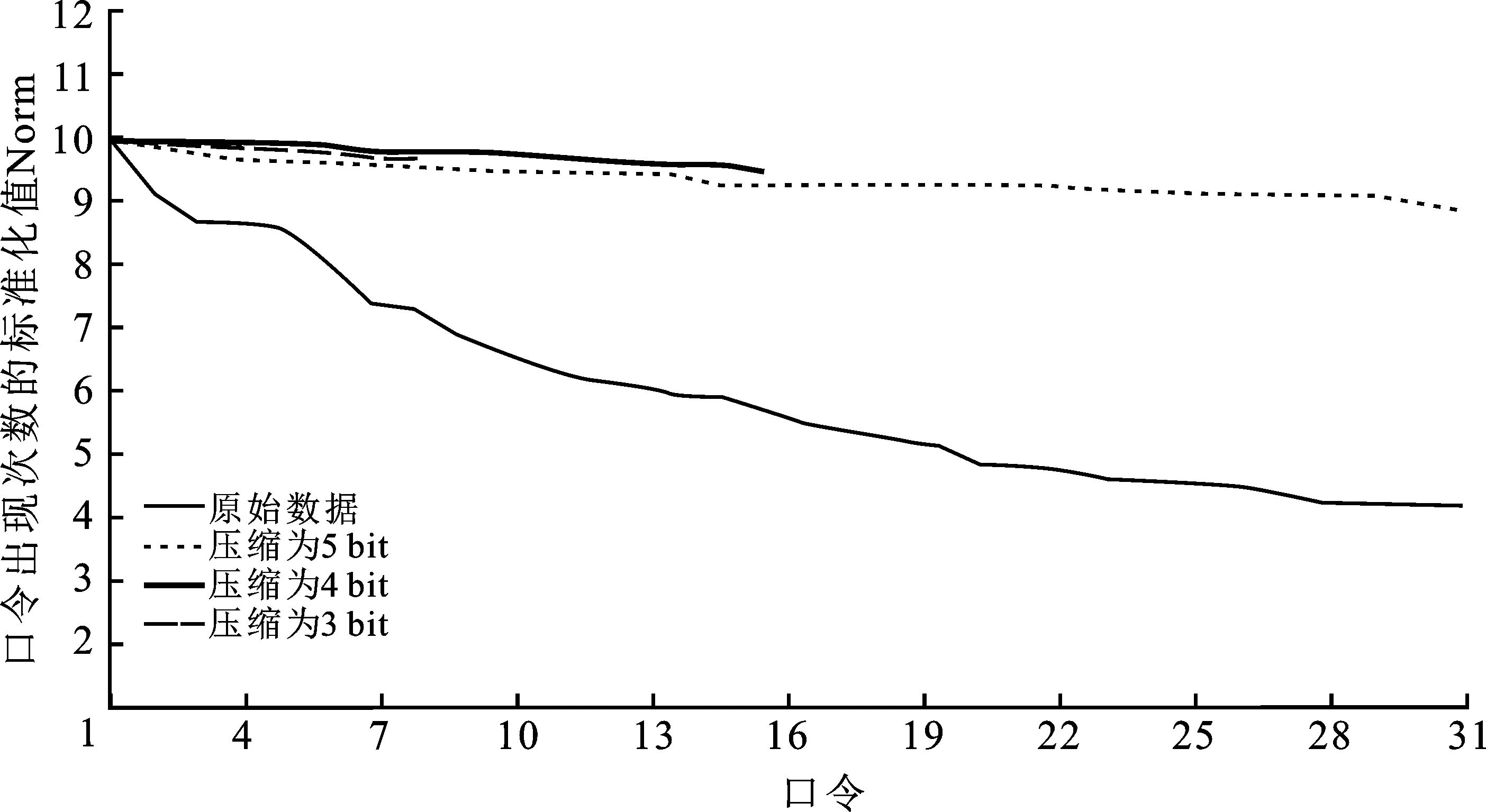
设计了一个基于口令的密钥提取方案(Password-Based Key Generation Scheme,PBKGS)。在PBKGS方案中,首先对口令进行二进制转换,得到一个n维二进制向量;之后测定口令库的熵值,并根据熵值确定下一步密钥提取矩阵的行的维数k;接下来确定密钥提取矩阵,先选取一个均匀随机的n维二进制向量,随后对该向量进行循环移位编码得到n×n维Toeplitz方阵,并根据上一步得到的矩阵行数k(k 将从口令中提取密钥的机制抽象为四步骤:口令的二进制转换、熵的测定与矩阵维数的确定、向量-矩阵编码以及密钥提取。下面将具体解释每一步的做法。 图2 基于口令的密钥生成方案(PBKGS) 2.2.1 口令的二进制转换 口令的二进制转换指的是将口令p由ASCII码[10]转换为二进制比特串。具体地说,假设口令p=(w1,w2,…,wt)包括t个ASCII码,其中wi均是ASCII码。由于ASCII码的取值范围为0~127,且127=27-1,因而可以将每一位ASCII码用一个7位长的二进制串来表示,即wi:=(i1,i2,…,i7)。最后,将每一位ASCII码的二进制展开并连接起来,就得到了口令p的二进制表示向量X=(x0,x1,…,x7t-1)。令n=7t。 2.2.2 熵的测定&矩阵维数的确定 在信息论中,熵是一种用来衡量随机变量的分布随机性大小的量度。一个随机变量的熵越大,这个变量的随机性就越强,越符合我们所说的“均匀随机”。在算法中,一个口令的熵值决定了最后能够提取的字符串的长度。所以检测一个口令库的熵是必不可少的一步。 熵的定义有很多种,香农(Shannon)熵、雷尼(Renyi)熵、最小(Minimal)熵,等等。在此,采用最小熵的定义来衡量口令库的熵(关于为什么采用最小熵,将会在2.3节中给出回答)。 假设经过计算,长度为nbit的字符串的熵为k,那么给定一个整数0 图3 熵的测定&矩阵维数的确定 2.2.3 向量-矩阵编码 由2.2.2节,在知道了提取矩阵A的维数k和n的值之后,先选取一个均匀随机的n维二进制列向量a=(a0,a1,…,an-1)T,然后将a作为一个n×n矩阵的第1列a(1),随后将列向量a的所有分量的位置循环后移一位,也就是说,此时a(2)=(an-1,a0,…,an-2)T,将a(2)作为这个n×n矩阵的第2列。并按照这种循环后移的方法,填充好后面的所有列。具体地说,这个n×n矩阵的第i列(1≤i≤n)填充的是列向量a(i)=(an-(i-1),an-(i-2),…,an-i)T。在填充好所有的列后,就得到了由列向量a生成的n×n维Toeplitz方阵。对Toeplitz方阵进行截断,保留方阵的前k行,得到k×n维Toeplitz矩阵A。具体见图4。 图4 Toeplitz矩阵生成示意图 在2.2.3节得到的k×n维的二进制矩阵A,在2.2.1节从口令中导出了n维二进制列向量X=(x0,x1,…,xn-1)T。由于矩阵A=(aij)与向量X都是二进制向量,可以通过矩阵乘法运算得到所提取的字符串(列向量)K=(K0,K2,…,Kk-1)T,其计算方式如下: K=AX, (2) 定理1在基于口令的密钥提取方案(PBKGS方案)中,若口令p的熵为H(p)=m,则所提取的字符串几乎均匀分布。若Uk代表{0,1}k上的均匀分布,则K的分布与Uk均匀分布的统计距离满足 Δ((a,K),(a,Uk))≤2-(m-k)/2。 (3) 证明在方案的向量-矩阵编码步骤中,首先选取了一个均匀随机的n维列向量a=(a0,a1,…,an-1)T,然后按照一个特定循环移位的编码方式,得到了一个n×n的矩阵A。从编码方式可以直观地看出,得到的n×n维的矩阵中每条与主对角线平行的所有斜线上的元素都是一样的,故编码得到的n×n维的矩阵是Toeplitz矩阵。随后将其截短,取其前k行,得到了一个k×n维的矩阵A,由于截短操作并不会对矩阵中元素的值进行改变,所以在截短后的矩阵A中,和原来未截短时n×n维的矩阵相比,截短后矩阵的自左上至右下的斜线上的元素仍然是一样的,也就是说,矩阵A同样也是Toeplitz矩阵。 由这个例子可以看出,熵损和提取出字符串与均匀分布之间的误差是息息相关的。牺牲的熵越多,那么提取出的字符串越均匀,但提取出的字符串越短。在实际应用中,可以根据实际情况来灵活地调整PBKGS方案的参数,如果要用的密码算法对密钥均匀性要求较高,就可以选择熵损大一些来获得更贴近均匀分布的字符串。否则,就将熵损定的小一些,提取更长的字符串。 使用了公开口令库DuDuNiu中的200 000条口令作为测试数据。为便于提取熵,选择其中长度超过10个ASCII码的口令串,并将其截取为10个ASCII码的截短口令,其中,每个ASCII码可以表示包括字母、数字、特殊符号在内共128种不同的符号。 由于测试使用的口令数目有限:10个ASCII码理论上可以表示12810种(约1021种)不同的口令,而最终得到的实验数据仅有 54 685 条,因此直接进行最小熵的统计会导致结果不准确,比如某个使用频率很高的口令并没有出现在测试集中;或者某个使用频率很低的口令在测试集中出现的次数却很多。为保证实验数据相对于口令组合数来说是充足的,选择将10个ASCII码的口令分为5段,每段包含2个ASCII码,这样每段能够表示的口令可能性仅为1282种(16 384 种)。这样,实验数据理论上是可以覆盖所有的1282种可能的,在这种情况下计算出的最小熵是比较可信的。 表1给出了分段检测最小熵的结果,从表中数据可以看出,每一段口令长度为14 bit(每个ASCII码可以用7 bit来表示,每一段有两个ASCII码),而最小熵仅为在2.9 bit至5.8 bit之间。这说明原口令串的随机性较差。将所有段的最小熵累加起来得出了完整口令最小熵的一个上界值,约为23.002 bit。在不考虑剩余哈希定理的熵损失的情况下,理论上最多可以从10个ASCII码长(70 bit长)的口令中提取23 bit均匀的字符串。 表1 口令各段统计的最小熵(每段两个ASCII码) 选择口令第三段,即第5、6个ASCII码(14 bit,最小熵5.783)进行了密钥提取实验,表2和图5为使用Toeplitz矩阵提取5 bit、4 bit、3 bit后熵值的对比。可以看出,在经过哈希函数压缩后,实际最小熵非常接近理论最小熵的最大值,说明从不太均匀的口令中提取出来的比特串非常接近均匀随机串。 表2 口令第3段的最小熵理论最大值与实际熵值的对比 图5 口令第3段的最小熵理论最大值与实际熵值的对比 图5给出了第三段口令以及第三段口令经过剩余哈希定理提取为5 bit、4 bit、3 bit长二进制串后均匀随机性的对比。由于原口令集数目过多,图中只给出了部分对比数据。图6中,横坐标i表示每个测试集合中按照出现次数由多到少排序的第i位口令,纵坐标表示口令出现次数的标准化值Norm,用Ni代表排在第i位的口令出现的次数,Norm值根据以下公式计算:Norm=Ni/N1。 可以很明显地看出,在进行提取之前(图6中细实线),口令值出现次数变化波动很大,而在提取为5 bit(图中短虚线)、4 bit(图中粗线)、3 bit(图中长虚线)后,曲线变化波动很小,非常接近理想情况,即数据集合中所有取值可能出现的次数几乎是一样的。 图6 对口令第三段进行压缩提取前后的均匀随机性对比 通过仿真实验可知,当选取两个ASCII码进行实验时,原始的口令的均匀随机性较差,而Teoplitz矩阵压缩后,可明显看出实际熵值已经非常接近理论上的最大熵值。也就是说,经过提取后的字符串的均匀随机性已经大大提高。 由上述结果,知道两个ASCII码长的口令段经过Teoplitz矩阵所确定的Universal Hash Function进行提取后所得到的二进制串具有很好的均匀随机性。 口令在日常生活中随处可见,用处极广。而随着祖国科技实力的强大,中国有了自己制定的标准密码算法,这些算法都可以用来保证个人信息的安全性。但现有的密码算法要求使用的密钥是一个均匀随机的字符串,显然口令并不均匀随机。为了解决这个问题,设计了一种可以从口令中提取均匀随机字符串的方法。并在公开口令库DuDuNiu上进行了测试。实验结果表明,笔者提出的方法可以有效地提取出口令的熵,得到几乎均匀随机的字符串。文中所提供的密钥提取方法有以下4个特点。 (1) 根据剩余哈希定理,利用Toeplitz矩阵作为Universal Hash Function(通用哈希函数)从口令中提取均匀随机的字符串作为密钥。 (2) Toeplitz矩阵的表示简洁,只需要一个二进制向量。Toeplitz矩阵作为一种Universal Hash Function,它的表示简洁,只需要一个二进制向量。作为二进制矩阵,Toeplitz矩阵的乘法和加法分别是“与”和“异或”运算,运算非常快。此外,Toeplitz矩阵的结构可以在进行矩阵乘法运算时,通过并行计算提高运算效率,因此进行密钥提取时算法效率很高。 (3) 密钥不需要存储,需要时可以随时由口令值进行恢复,而恢复口令所需要的信息矩阵信息可以公开,且公开信息矩阵不会影响密钥的均匀随机特性。 (4) 所产生的均匀随机的字符串既可以作为认证密钥,又可以作为加密密钥,扩展了口令的密码功能。 对以上的研究结果进行如下分析,并给出相应的建议: (1) 因为所提取的均匀随机字符串较短,故建议增加口令的长度可以提取更长的均匀随机串。研究结果显示,最多可以从10个ASCII码长的口令中提取出13 bit的均匀随机串,均匀随机串长度约为原口令长度的18.6%,长度较短。根据分析,导致提取出的均匀随机串长度短的原因主要有两个方面:一是口令的长度短、熵值低,根据分段估熵的结果,完整口令的最小熵不超过23 bit,因此本身能从口令中提取的随机比特就很少;二是根据剩余哈希定理,为保证压缩后的二进制串尽可能接近均匀随机串,还需要额外牺牲掉一部分熵值。因此,建议增加口令的长度可以提取更长的均匀随机串。一方面,增加口令长度可以使得口令的原始熵值增加。简单的实验表明,当口令长度变为原先的2倍时,其最小熵值大约也为原先的2倍。另一方面,使用剩余哈希定理的熵损失是一个定值,随着口令长度的增加,提取出密钥的长度将增加得更快。举个例子,原始口令长度为10个ASCII码长,最小熵为23,可以提取13 bit的均匀随机串,假设口令长度变为原先的n倍,最小熵也变为原先n倍,即23nbit,那么在保证同样的均匀随机性的条件下,可以牺牲10 bit,得到(23n-10) bit长的均匀随机串。例如n=5时,可以得到105 bit的密钥。这样通过增加口令长度,可以很有效地增加所提取的密钥长度。 (2) 可以由单个口令中生成多个密钥。通过PBKGS方案,用户可以从口令p中提取一个均匀随机的密钥K。假设密钥长度是足够的,进一步考虑如何从一个密钥中得到多个密钥。国际组织IETF给出了如何使用HMAC算法对密钥进行扩展[12],国家商用密码管理办公室发布的《SM2密码算法使用规范》标准[13]中介绍了一个密钥扩展函数(Key Derivation Function,KDF),通过KDF,就可以实现从一个密钥中扩展出多个密钥。 具体来说,当利用PBKGS从口令中提取出了一个密钥K后,定义一个计数器Counter(初始化为1,每一次计算后都增加1),将Counter和密钥K作为密钥扩展函数的输入,计算Ki=KDF(K,Counter)。根据密钥扩展函数的性质,就得到了多个密钥K1,K2,…,这些密钥可分别用于微信、邮箱、QQ认证、文件加密中等应用中的密码算法。即使用户有一个密钥Ki泄露,也可以保证其他密钥Kj,j≠i的安全性。具体见图7。 (3) 从口令里提取的密钥应用于不同的密码方案。这里简单地介绍密钥用于认证、加密的场景。 认证:用户A希望在应用服务器注册个人账号,他/她可以使用口令提取的均匀随机串作为密钥,产生一个基于身份的认证符,并把认证符发给服务器用于以后的身份认证。当用户A需要登录时,只需要用同样的口令提取出均匀随机串作为密钥,再次产生基于身份的认证符,发送给服务器即可验证通过。 加密:用户A希望加密一个Word文档,他/她可以通过口令提取的均匀随机串作为对称加密算法的密钥,当用户A需要解密时,只需要用同样的口令提取出随机串。对于对称加密算法来说,加密密钥与解密密钥是一样的,因此用户A可以正确解密密文,获得原始文档。 图7 密钥扩展方案示意图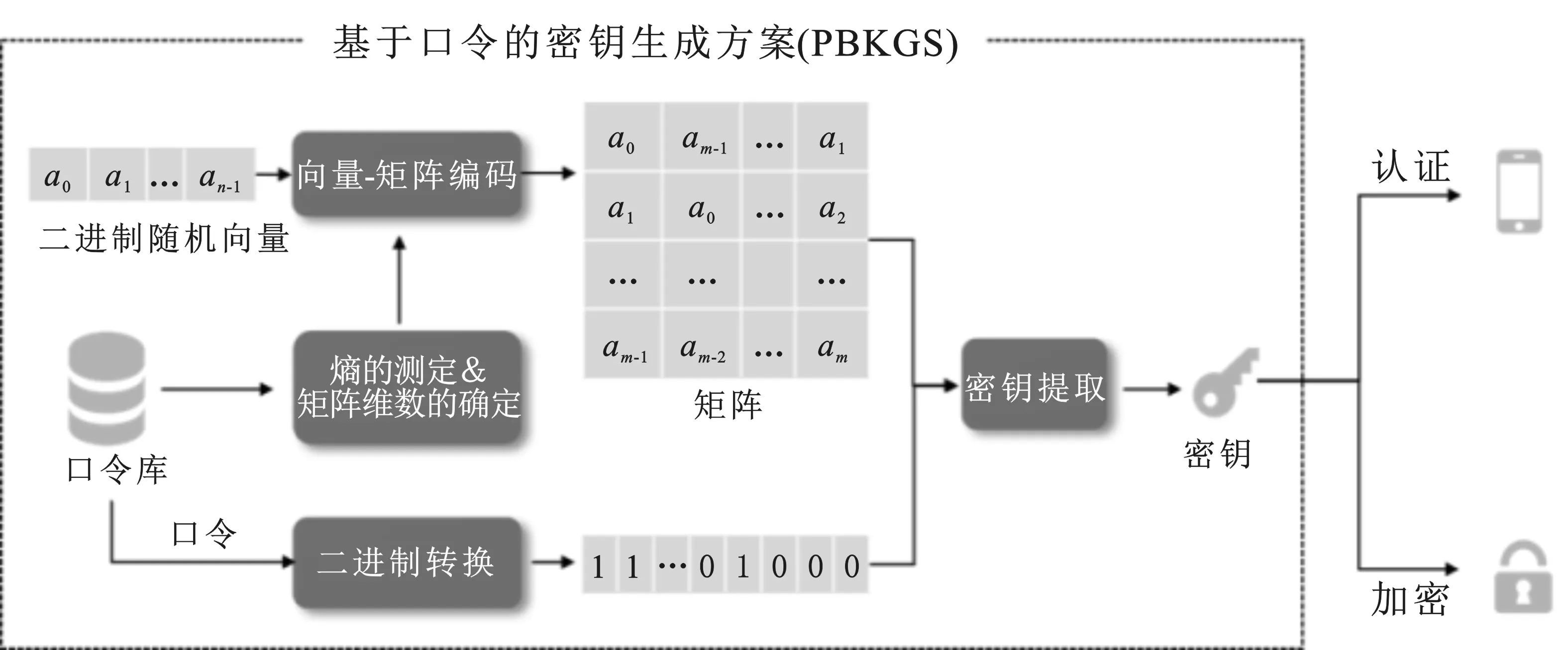

2.3 密钥提取及原理
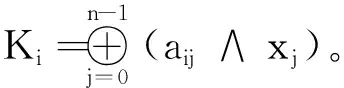
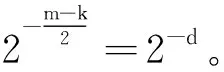

3 结果测试与分析




4 结论和建议