(n,m)函数抗差分功耗攻击指标的研究综述
2021-01-29陈智雄卓泽朋杜小妮
周 宇,陈智雄,卓泽朋,杜小妮
(1.保密通信重点实验室,四川 成都 610041;2.莆田学院 福建省应用数学重点实验室,福建 莆田 351100;3.淮北师范大学 数学科学学院,安徽 淮北 235000;4.西北师范大学 数学与统计学院,甘肃 兰州 730070)
(n,m)函数是对称密码算法的基本部件之一,其研究重点在设计和分析两个方面。设计主要是通过数学方法构造出满足多种密码学性质的函数,而分析主要是研究函数的各种密码学指标,这些密码学指标往往与其对应的攻击紧密联系在一起。从(n,m)函数面对的各种攻击来看,可以将密码学指标分为两大类:
(1) 基于数学的传统攻击手段,例如线性攻击、差分攻击、代数攻击、相关攻击等,一些指标主要有非线性度、相关免疫度和代数免疫度等;
(2) 基于物理的差分功耗分析手段,例如差分功耗攻击,主要有信噪比[1]、透明阶[2]和混淆系数[3]等。
文中重点讨论信噪比、透明阶和混淆系数这三个指标,以及这些指标与传统密码学指标的关系等。
差分功耗攻击(Differential Power Attack,DPA)[4]是能量分析中一种强有力的攻击手段,其原理是通过统计密码设备或者密码算法在加密运算过程中泄漏的功耗消耗特征,来破译出一些密钥信息。该方法最早是在1999年由KOCHER等人[4]提出,当时是对分组密码数据加密标准(Data Encryption Standard,DES)进行了差分功耗攻击。这种方法后来被广泛用于公钥密码算法和分组密码算法的安全分析中。而在实验层面进行差分功耗攻击是在2002年由MESSERGES等人[5]提出。在此基础上,汉明距离功耗模型被BRIER等人[6]提出,该模型验证了相关功耗分析(Correlation Power Analysis,CPA)攻击,实验结果进一步表明,CPA在某些方面相对DPA有较大优势,这也是后来CPA被广泛使用的原因之一。以上的实验和一些模型都是针对非线性S盒展开分析,S盒作为对称加密算法的主要非线性部件之一,对算法的安全性起着关键性作用,但是传统密码学性质好的S盒未必能抵抗差分功耗分析。因此,必须对S盒的抗差分功耗攻击指标进行系统研究。下面将从差分功耗分析角度给出三个密码学指标(信噪比、透明阶和混淆系数)的发展现状。
第1个指标:信噪比(Signal-to-Noise Ratio,SNR)。该指标是在2004年8月的CARDIS会议上被GUILLEY等人[1]提出。首先他们基于传统密码分析的框架对信息泄漏进行完整建模,对于攻击者来说可以获取密钥猜测值的Hamming权重的自相关值。该模型表明,当S盒抵抗线性密码分析能力增强时,S盒对应的信噪比值也将随之增大。但是从S盒抵抗DPA角度来说,信噪比越小,抵抗DPA越好。这就表明S盒的信噪比和S盒抵抗线性密码分析之间存在着制约关系,两者不能同时达到最好。通过信噪比模型和定义可以看出,非线性S盒的噪声对密码算法的DPA信号起着决定性作用。随着该指标出现也产生了一些研究结果[7]。
第2个指标:透明阶(Transparency Order,TO)。该指标是在2005年的FSE会议上被PROUFF[2]首次提出。文献[2]基于差分功耗思想,建立了多入多出(n,m)函数与汉明距离模型的紧密关系,得到了S盒的透明阶与传统的一些密码学性质不能同时达到最好。随着国内外学者研究的深入,也衍生出了改进的透明阶概念(Redefining Transparency Order,RTO)[8]和修改的透明阶(Modified Transparency Order,MTO)概念[9]。在新指标和旧指标的共同指引下得到了一系列研究成果[10-12]。
第3个指标:混淆系数(Confusion Coefficient,CC)。该指标是在2012 年的密码硬件和嵌入式系统国际研讨会上被FEI等人[13]提出。研究表明,S盒的混淆系数值越大,S盒抵抗DPA能力就越强。基于FEI等人的结果,PICEK等人[14]在2014 年计算了不同大小的 S 盒的非线性度,得到了混淆系数方差。同年,邱爽等人[15]为了降低维数和混淆系数的个数,对原始混淆系数进行了修订,给出了新的混淆系数定义。基于该新定义,重新计算了DES针对各个备选密钥的功耗差(Difference of Means,DoM)期望的分布。实验结果与利用修改后的混乱系数计算得到的DoM期望值相符。
因此,笔者试图从数学理论角度来综述(n,m)函数的这三个指标的研究进展,而不考虑其背后的物理实验背景。
1 基本概念
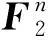
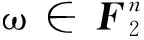


2004年GUILLEY等人在研究DPA信号时提出了信噪比(SNR)概念[1]。
定义1[1]设F=(f1,f2,…,fm)是一个(n,m)函数,则函数F的信噪比(SNR)定义为
(1)
紧接着,在2005年的FSE会议上,PROUFF扩展了GUILLEY等人提出的多比特DPA攻击[1]和功耗模型,提出了汉明重量模型,建立了S盒与DPA攻击的关系,给出了(n,m)函数的透明阶概念(TO)[2]。
定义2[2]设F=(f1,f2,…,fm)是一个(n,m)函数,则函数F的透明阶(TO)定义为
(2)
2017年CHAKRABORTY等人在研究(n,m)函数的TO基础上,发现了TO的冗余,所以提出了改进透明阶概念(RTO)[8]。
定义3[8]设F=(f1,f2,…,fm)是一个(n,m)函数,则函数F的改进透明阶(RTO)定义为
(3)
2019年周永彬等在研究(n,m)函数的RTO基础上,通过多比特DPA(Multi-bit DPA)和变型多比特DPA(Variant multi-bit DPA)实验,发现线性 (n,m)函数可以完全抵抗变型多比特DPA攻击,但是线性(n,m)函数很容易受到DPA攻击,为此提出了修改的透明阶概念(Modified Transparency Order,MTO)[9]。
定义4[9]设F=(f1,f2,…,fm)是一个(n,m)函数,则函数F的修改透明阶(MTO)定义为
(4)
从定义2~4可以看出,TO与F=(f1,f2,…,fm)的分量函数自相关函数紧密联系在一起,而RTO和MTO与F=(f1,f2,…,fm)的分量函数自相关函数和互相关函数紧密联系在一起;定义3和4惟一不同在于绝对值的位置,这决定了在DPA攻击中泄露的信息多少。
2012年,FEI等人在研究DPA统计模型时,建立了DPA成功率与密码算法之间的定量关系。基于该定量关系,用一种新混淆分析法提取密码算法的边信道特性,提出了(n,m)函数的混淆系数概念(CC)[3]。
定义5[3]设F=(f1,f2,…,fm)是一个(n,m)函数,则函数F的混淆系数(CC)定义为
(5)
其中,σ2为方差函数,κ(ki,kj)=Ep[(L(F(ki+p))-L(F(kj+p))2)],ki,kj分别表示第i个和第j个密钥值,p为明文,L为泄露函数。
受篇幅限制,布尔函数的相关其它概念(例如扩散性、代数免疫、相关免疫、全局雪崩准则等)请参考文献[16]。
2 (n,m)函数的信噪比研究进展
GUILLEY等人[1]得到了平衡(n,m)函数信噪比的上下界、非平衡(n,m)函数信噪比的下界、Bent(n,m)函数信噪比的下界,并证明了当(n,m)函数抵抗线性密码分析能力增加时,信噪比也将随之增加。2020年,周宇等人研究了布尔函数(即(n,1)函数)的信噪比[7],给出了任意n元函数的信噪比紧的上界和紧的下界,以及下界与非线性度的关系,得到了n元函数信噪比与2个n-1元分解函数信噪比的关系。特别地,对于平衡布尔函数,给出了信噪比更紧的上界和下界,最后给出了两个n元函数相加与两个n元函数乘积的信噪比与各自信噪比的关系,同时也给出了4元、5元平衡布尔函数信噪比的分布表。
2.1 (n,m)函数的信噪比
对于F=(f1,f2,…,fm)的信噪比与分量函数的信噪比有如下关系。
定理1[7]设F=(f1,f2,…,fm)是一个(n,m)函数,则
(6)
但是对于由分量函数信噪比决定的F=(f1,f2,…,fm)的信噪比上界,仅能给出(n,2)函数的结果,对于m≥3,很难给出精确的刻画。
定理2[7]设F=(f1,f2)是一个(n,2)函数,则
(7)

(8)
进而得出
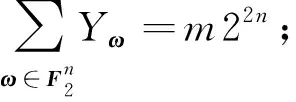
在此基础上,得到一些(n,m)函数信噪比的上界或者下界,具体如表1[1]所示。

表1 (n,m)函数信噪比上界或者下界

表2 5元平衡布尔函数的信噪比分布
2.2 布尔函数的信噪比
当m=1时,(n,m)函数就是n元布尔函数,其信噪比性质较(n,m)函数刻画得更清晰。其结果如下。
定理3[7]设f∈Bn,则1≤SSNR(f)≤2n/2,其中左边等号成立,当且仅当f是仿射函数,而右边等号成立,当且仅当f是bent函数。
进一步可以知道f的信噪比与非线性度的关系:SSNR(f)≥2n/(2n-2nl(f))。
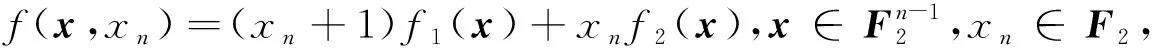
(9)

而对于两个变量不交的函数,其和函数和积函数的信噪比结果如下。
定理5[7]设f∈Bn,g∈Bm,则
(1)SSNR(f+g)=SSNR(f)SSNR(g);

而对于满足一定扩散性的布尔函数来说,其信噪比上界如下。

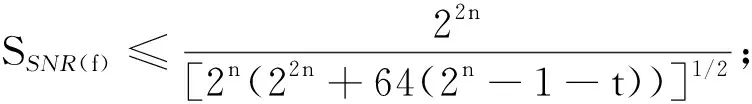

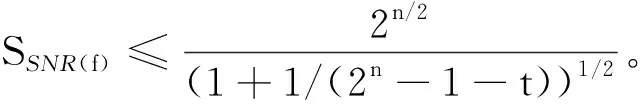
通过程序计算[7]可知,4元平衡布尔函数的SNR为4值分布:{1.000 000,1.705 606,2.000 000,2.529 822},而5元平衡布尔函数的SNR为18值分布:{1.000 000,1.302 062,1.705 606,1.735 444,2.000 000,2.157 440,2.285 714,2.359 071,2.439 977,2.529 822,2.630 384,2.873 685,3.023 716,3.200 000,3.411 211,3.670 652,4.000 000,4.437 602}。5元平衡布尔函数的信噪比具体分布如表2所示。
3 (n,m)函数的透明阶研究进展
在(n,m)函数的透明阶发展中出现了三个不同概念,依次介绍如下。
(1) 2005年,PROUFF首次在FSE上提出(n,m)函数的透明阶(TO)概念[2],在DPA攻击的模型中发现了S盒的透明阶与S盒的非线性不能同时达到最好,即如果S盒抵抗线性攻击的能力越强,S盒抵抗DPA攻击的能力就越弱。紧接着,CARLET系统研究了高非线性S盒的透明阶,得到了该S盒的透明阶下界[26]。该结果反映了透明阶与非线性度的关系,进一步他也研究了其它一些高非线性函数(例如逆函数、Gold 函数、Kasami 函数),发现在理论上这些S盒具有较差的透明阶。后来,FAN等人[27]通过引入一个精心设计的阈值滤波器提出了一种计算S盒透明阶的快速实现方法,基于此,给出了两种S盒透明阶的优化计算技术。MAZUMDAR等人[28]在2013 年得到了一些偶数元和奇数元S盒的透明阶上界和下界,利用搜索方法得到了一类TO值优于AES算法中的S 盒。2014年PICEK等人[29]研究了轻量级分组密码PRINCE,通过进化算法得到了非线性度为4且透明阶最低的S盒,以此生成具有改进DPA相关特性的S盒。后来,SARKAR等人[30]针对(n,n)函数,基于差分能量分析回答了如何在仿射等价下对S盒的选择问题。同年MAZUMDAR[31]找到了在传统密码特性(如高非线性和低GAC绝对指示符)和透明阶指标方面都较好的S盒。
(2) 2017年,CHAKRABORTY等人指出TO指标存在一定的局限性,给出了修改的透明阶指标(RTO)[8]。在该概念的引导下,PICEK等人基于遗传算法和随机搜索等算法搜索找到了一些抵抗 DPA好的S盒[29]。
2017年程让在其硕士论文[10]中对RTO进行了研究,推导出了RTO下界与分量函数Walsh谱值的关系,给出了RTO与非线性度之间的一种制约关系,并分别基于Maiorana-McFarland函数构造法和Bracken-Leander函数构造法得到了平衡且具有较低RTO的(4,4)函数。2019年WANG等人[11]针对TO和RTO研究了布尔函数的透明阶,给出了由非线性度决定的RTO的下界,提出了2种具有良好透明阶的无限类平衡半bent函数,同时也给出了择多函数(the majority function)、隐藏重量函数(the hidden weighted bit function)、Carlet-Feng函数、旋转对称布尔函数(rotation symmetric Boolean functions)的透明阶。
(3) 2019年周永彬等人[9]指出多比特DPA攻击中RTO定义的不足,提出了修订的透明阶概念(MTO),对某些S盒进行了实验仿真,进一步分析了16类最优(4,4)函数的仿射等价类MTO分布规律。
3.1 (n,m)函数的透明阶
首先,给出2005年由PROUFF得到的扩散准则与透明阶关系[2]。
定理7[2]设F=(f1,f2,…,fm)是一个(n,m) 函数(m≤n)。如果F满足t阶扩散准则,则
(10)
紧接着,对于任意(n,m)函数来说,其透明阶介于0和m之间。
定理8[2]设F=(f1,f2,…,fm)是一个(n,m) 函数,则0≤TTO(F)≤m。
而对于(n,m)函数来说,其透明阶的下界与分量函数的Walsh谱有如下关系[26]。
定理9[26]设F=(f1,f2,…,fn)是一个(n,n) 函数,则
(11)
CHAKRABORTY等人在TO的基础上,分析了仿射变换下RTO的变化情况,指出对 (n,m) 函数的输入变量做仿射变换不改变RTO的值,而对(n,m) 函数的输出值做某个仿射变换后RTO的值会发生改变[8]。
定理10[8]设F=(f1,f2,…,fm)是一个平衡(n,m) 函数,则对任意的n阶可逆矩阵A,有RRTO(F∘A)=RRTO(F)。
2017年程让在其硕士论文中证明了分量函数非零线性组合后的函数最大Walsh谱与RTO的关系[10]。
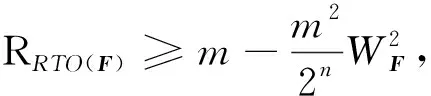
结合文献[8]和[9]的结果,可以看到MMTO(F)和RRTO(F)有共同的下界。
定理12[8-9]设F=(f1,f2,…,fm)是一个(n,m) 函数,则MMTO(F)和RRTO(F)有共同的下界,即
(12)
3.2 最优(4,4) 函数的透明阶分布
对于任意的F=(f1,f2,…,fm),文献[9]证明了对任意的n阶可逆矩阵A有MMTO(F)=MMTO(F∘A),但存在某些n阶可逆矩阵A能使得MMTO(F)≠MMTO(A∘F)。这也就表明MTO不是仿射变换下的不变量。根据该结论就可以给出16类最优 (4,4)S盒的仿射等价S盒(共20 160×16个)的各类透明阶分布图。图1为TO的分布图(可知TO为9值分布),图2为RTO的分布图(可知RTO为30值分布),图3为MTO的分布图(可知MTO为11值分布)。

图1 TTO(A∘Gi)的分布图
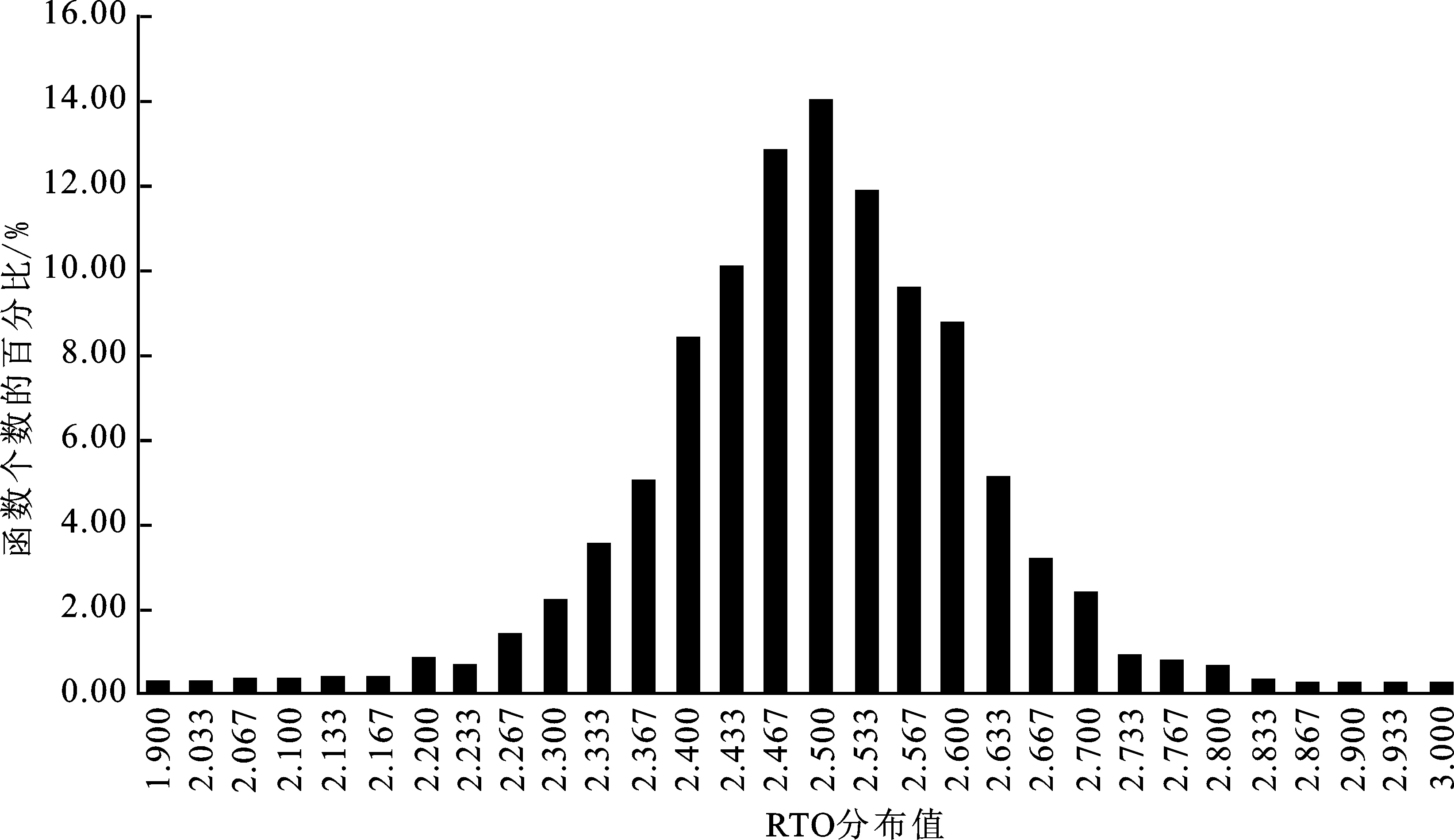
图2 RRTO(A∘Gi)的分布图

图3 MMTO(A∘Gi)的分布图
3.3 布尔函数的透明阶
当m=1时,(n,m)函数F就是n元布尔函数,此时有TTO(F)=RRTO(F)=MMTO(F)。
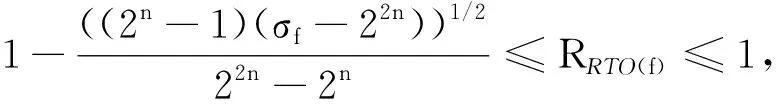
4 (n,m)函数的混淆系数研究进展
文献[29]基于汉明重量对给定的CPA选择函数给出了计算混淆系数的方法。对所有密钥对ka,kb(ka≠kb),计算κ(ka,kb)=E[(HW(F(in+ka))-HW(F(in+kb)))2]。
定理14[29]设F=(f1,f2,…,fm)是一个(n,m) 函数,则对密钥的第ki,kj,kh对应的三方混淆系数如下:
(13)
针对F=(f1,f2,…,fm)进行DPA时各个备选密钥的功耗差(DoM)期望的分布,FEI等人[13]得到如下结论:
定理15[13]设F=(f1,f2,…,fm)是一个(n,m) 函数,kc为错误密钥猜测值,kg为正确密钥,kc和kg对应的DoM分别为δc和δg,则对Δ(kc,kg)有
(1)E[Δ(kc,kg)]=2κ(kc,kg)ε;


而关于混淆系数与成功率,FEI等人[3]得到成功率的公式。
定理16[3]基于CPA泄露模型,在对称密钥假设下,CPA的渐进成功率为
(14)
其中,K**表示另外一个(NK-1)(NK-1)维混淆矩阵。
在混淆系数计算中,首先得根据不同的密钥ki,kj计算出κ(ki,kj)。为此,文献[14]基于仿射变换给出了16类最优4比特S盒[17]和一些公开算法中S盒的κ值大小(如表3所示)。
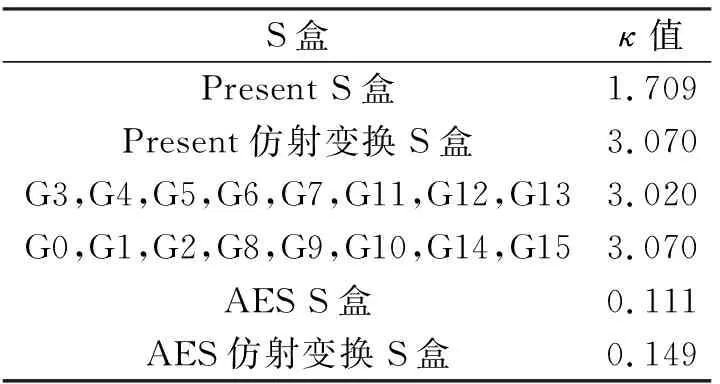
表3 一些 (4,4) S盒κ值
2014年,邱爽等人[15]指出,FEI[3]提出的混淆系数定义中存在冗余,并且修改了混乱系数的定义,重新构建了DPA模型中算法相关的部分,其定义如下:
定义6[3]设F=(f1,f2,…,fm)是一个(n,m)函数,则函数F的修改混淆系数(RCC)定义为
(15)
其中,of表示两个密钥之间的异或关系KS1+KS2,假设F(·)b表示选定F的某一位的输出。
可以看出,RRCC(F)只与两个密钥之间的异或值相关,和混淆系数κ值的关系为
RRCC(KS1+KS2)=κ(KS1,KS2) ,
(16)
根据这个关系式可知,修改后的混淆系数在个数方面有较大的下降。
根据定义6,邱爽等人[15]针对DES算法得到了DPA各个假设密钥产生的均值差,计算了修改混淆系数,从实验角度验证了修改混淆系数的合理性。
5 一些(n,n) S盒的常用密码学指标值对照
首先,对于一些公开算法中(4,4) S盒,2014年文献[29]给出了这些常用密码学指标的对照表(如表4所示)。

表4 一些 (4,4) S盒的各种密码学指标对照表
然后,对于一些公开算法中(8,8) S盒,2018年文献[32]给出了这些常用密码学指标的对照表(如表5所示)。
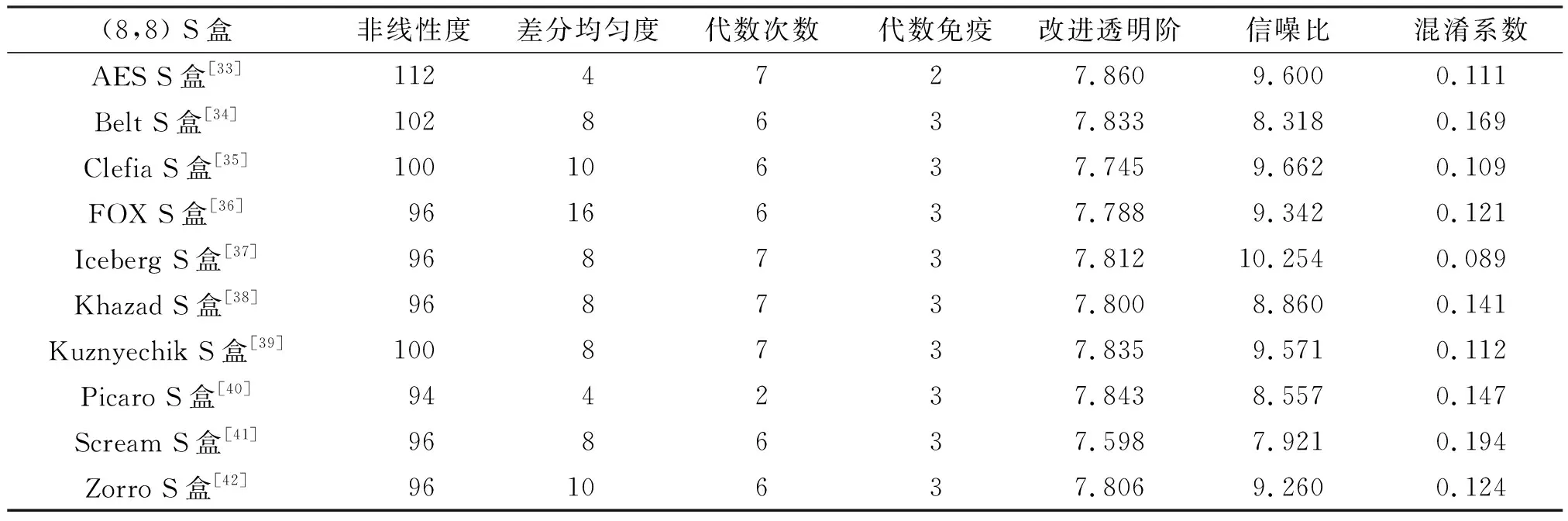
表5 一些 (8,8) S盒的各种密码学指标对照表
最后,对于一些构造得到的(8,8) S盒,文献[32]给出了这些常用密码学指标的对照表(如表6所示)。
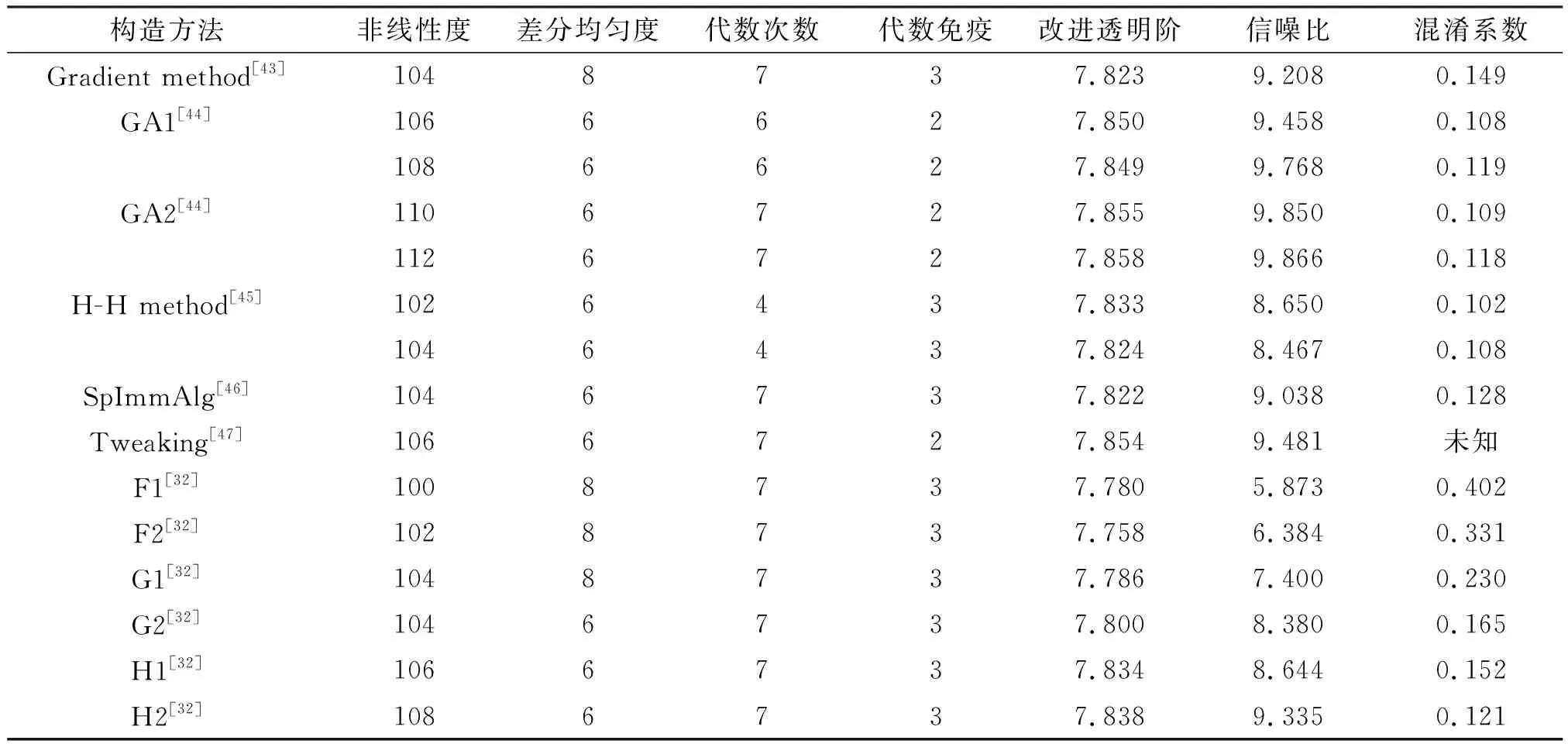
表6 一些 (8,8) S盒构造方法的各种密码学指标对照表
6 值得进一步研究的问题
(n,m)函数是对称密码算法中的基本部件,其安全性对密码算法安全性起着重要作用。经过国内外学者多年来的共同努力,在(n,m)函数抵抗差分功耗攻击方面已经取得了丰富的成果。文中重点综述了(n,m)函数的三个密码学指标(信噪比、透明阶和混淆系数)。由于文章篇幅所限,对如何构造满足良好信噪比、透明阶和混淆系数的(n,m)函数的研究成果介绍相对简单,感兴趣的读者可以进一步查阅相关参考文献。结合目前(n,m)函数的这三个密码学指标的研究结果,以及抗侧信道模型的分析,作者认为下列问题值得进一步研究:
(1) 信噪比、透明阶和混淆系数分别与传统密码学指标的关系已经研究出了一些结论,但是还不够详尽,需要进一步研究。
(2) 信噪比、透明阶和混淆系数之间相互的制约关系研究的较少,特别是针对某些密码结构,例如某些特殊构造的4比特S盒[48]、线性移位寄存器[49],等等。
(3) 构造符合特定场景需求且满足一定密码学性质的S盒是密码算法设计的重要研究方向,特别是构造同时抵抗侧信道攻击和抵抗传统密码攻击(某些特殊模型的快速代数攻击[50])的S盒是研究的重点。
