浅析Xiao-Massey定理的意义和作用

冯登国

(中国科学院 软件研究所，北京 100190)

相关攻击从对基于线性反馈移位寄存器(Linear Feedback Shift Register，LFSR)的序列密码的分析起步，最早是由BLASER等人[1]提出的。真正有价值的工作是由SIEGENTHALER[2]提出的非线性组合生成器的分别征服相关攻击，其基本思想是利用组合函数的输出与输入分量或者某些输入分量子集之和的相关性，穷搜索某个特定LFSR的初始状态或者某几个LFSR 的初始状态，而各个LFSR 的初始状态就是非线性组合生成器的子密钥，这就是最早的相关攻击。“分别征服(divide-and-conquer)”起名于一种图论算法，体现了“分而治之”的思想，意为将一个待求解的问题分成许多子问题，然后对每个子问题求解，最后再综合求解。为了对抗这种相关攻击方法，SIEGENTHALER提出了布尔函数的相关免疫的概念[3]，用于度量和刻画非线性组合序列密码抵抗分别征服相关攻击的能力。相关免疫布尔函数是一类重要的密码函数，其频谱特征刻画是构造和分析这类函数的理论基础。肖国镇(G.Z.Xiao)教授和梅西(J.L.Massey)教授于1988年给出了相关免疫布尔函数的沃尔什(Walsh)频谱特征刻画[4]，这一工作被国内外学者称之为Xiao-Massey定理。关于相关免疫函数更多的进展可参阅文献[5-6]及其参考文献。

首先回顾了Xiao-Massey定理，其次简述了Xiao-Massey定理的意义，然后阐释了Xiao-Massey定理的作用，最后总结了全文。

1 Xiao-Massey定理

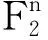
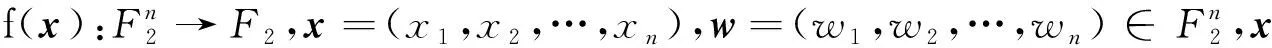
(1)

式(1)的逆变换(又称反演公式)为

(2)

上面各式中的求和是指实数求和，式(2)可由式(1)推导出。

计算沃尔什变换有快速算法[5]，称之为快速沃尔什变换，其时间和存储复杂度分别为O(n2n)和O(2n)。

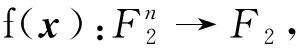
(3)

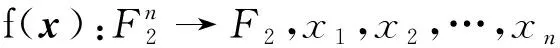
则称f与变元xi1，xi2，…，xim统计无关(也称统计独立)。如果f与x1，x2，…，xn中的任意m个变元都统计无关，则称f是m阶相关免疫的。特别地，如果f既是平衡的，又是m阶相关免疫的，则也称f是m阶弹性的。

Xiao和Massey[4]用沃尔什谱刻画了相关免疫函数的特征，并给出了一个非常重要的引理，国际上称之为Xiao-Massey引理。

由Xiao-Massey引理可推出以下结论。

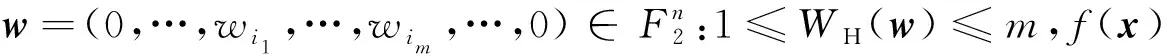
下面的引理2给出了f与变元xi1，xi2，…，xim统计无关的重量特征。

引理2设f(x)如定义2中所述，f(x)与变元xi1，xi2，…，xim统计无关，则WH(f)=2mk0，k0为非负整数。

证明：因为f(x)与变元xi1，xi2，…，xim统计无关，因此，

P(f=1|xi1，xi2，…，xim)=P(f=1) 。

由

且

得

即

WH(f)=2mWH(f′) 。

其中，f′表示给定xi1=ci1，xi2=ci2，…，xim=cim的条件下，f关于n-m个变元{x1，x2，…，xn}{xi1，xi2，…，xim}的函数。

下面给出Xiao-Massey定理。

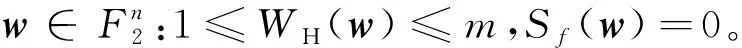
可由定理2直接推出f(x)与变元xi1，xi2，…，xim统计无关的谱特征。

2 Xiao-Massey定理的意义

Xiao-Massey定理具有以下重要意义：

(1) 该定理为频谱技术在密码学中的应用开辟了一条广阔的道路。自从Xiao-Massey定理提出以来，人们高度重视频谱技术在密码设计和分析中的应用。一方面积极发展和完善频谱理论与方法；另一方面深度挖掘频谱技术在密码学中的应用与作用。主要包括以下研究内容：

① 适用于研究高阶逼近的频谱理论与方法，如二阶沃尔什谱、m阶沃尔什谱等；

② 适用于研究域、环等代数结构上的密码函数的频谱理论与方法；

③ 适用于研究多输出函数的频谱理论与方法；

④ 密码函数的各种性质的频谱特征刻画；

⑤ 频谱技术在密码分析中的应用，如最佳仿射逼近分析[7]、最大相关攻击[5]等；

⑥ 探索其他频谱技术在密码学中的应用。

(2) 该定理为研究相关免疫函数找到了一个新的研究工具，创新性地刻画了相关免疫布尔函数的频谱特征。起初人们对相关免疫函数的认识非常有限，Xiao-Massey定理的提出，打开了人们认识相关免疫函数的视野，给出了若干刻画相关免疫函数特征的方法，并进一步刻画了相关免疫阶与其他非线性准则之间的关系。主要包括以下研究内容：

① 相关免疫函数的特征刻画，如特征矩阵的各种刻画以及与组合设计和纠错编码中对偶距离之间的关系等；

② 相关免疫阶与其他非线性准则之间的关系，如非线性次数、非线性度、线性结构、扩散准则等；

③ 高度非线性相关免疫函数的构造与计数；

④ 满足各种密码学性质的密码函数的构造与计数；

⑤ 探索新的非线性度量准则。

(3) 该定理将概率统计问题转化为代数问题。相关免疫函数的判定本是一个计算概率统计的问题，但通过Xiao-Massey定理将其转化为计算某些特定点的谱值是否为零的代数问题。由于计算沃尔什谱有快速算法，因此，这样做不仅可行，而且具有重要的实际意义。这就迫使人们不得不重视以下研究问题：

① 各种频谱技术的快速计算方法；

② 概率统计问题与代数问题的相互转化方法。

(4) 该定理将时域处理问题转化为频域处理问题。直接处理相关免疫布尔函数涉及的运算是逻辑运算，需要在时域上处理问题，有时不是很方便，但通过Xiao-Massey定理将其转换为频域上的运算，也就是实数域上的算术运算，这样处理起来更加方便和简单。这种思想在科学研究中非常重要，它将A中的问题Q通过变换T转化为B中的问题T(Q)，而在B中T(Q)的研究比较简单并可通过T(Q)的研究获得Q的特征，即使不能求出T-1，这也是十分有价值的。

3 Xiao-Massey定理的作用

Xiao-Massey定理本质上给出了相关免疫函数的另一个等价定义，在一些场景中使用起来十分方便。Xiao-Massey定理在相关免疫函数的判定、相关免疫函数的构造与计数、相关免疫阶与其他非线性准则(如非线性次数、非线性度等)之间的关系刻画、序列密码分析等方面具有重要的作用和价值。本节仅给出Xiao-Massey定理在3个方面的作用。

3.1 相关免疫函数的判定

由Xiao-Massey定理可推出以下结论。

注意到

(-1)f(x)=1-2f(x) ，

且

因此，Sf(w)=0，当且仅当f(x)+w·x是平衡的。从而，推论3得证。

由推论3易推出以下结论。

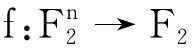
下面的算法1给出了构造相关免疫函数的一个递归方法[3]。

算法1设f1和f2分别是n个变元的m阶相关免疫函数，令

则f是n+1个变元的m阶相关免疫函数。次数∂0f=max{∂0f1，∂0f2}+1。

可直接利用Xiao-Massey定理判定算法1构造出的f是n+1个变元的m阶相关免疫函数。

3.2 相关免疫阶与非线性次数之间的关系

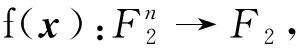
(4)

其中，a0，ai1，i2，…，ir∈F2，求和符号“∑”是指在F2上的求和。式(4)称为f(x)的多项式表示。常将式(4)按变元升幂及下标的字典序写成

f(x)=a0+a1x1+a2x2+…+anxn+a1，2x1x2+…+an-1，nxn-1xn+…+a1，2，…，nx1x2…xn。

(5)

式(5)称为f(x)的代数正规型。任一确定的n个变元的布尔函数f(x)的代数正规型是惟一的。一个乘积项(也称单项式)xi1xi2…xir的次数定义为r，非零常数项的次数定义为0，0的次数定义为-。布尔函数f的次数定义为f的代数正规型中具有非零系数的乘积项中的最大次数，记为∂0f。当∂0f=1时，称f(x)为线性布尔函数；当∂0f≥2时，称f(x)为非线性布尔函数。

现在观察f(x)的最高次项x1x2…xn出现的充要条件。易知

这里“∑”是实数求和，即a1，2，…，n=WH(f) mod 2。可得a1，2，…，n=1，当且仅当WH(f)为奇数。由此可见，当WH(f)为偶数时，a1，2，…，n=0，即最高次项不出现。特别地，平衡布尔函数无最高次项x1x2…xn。

下面说明相关免疫阶和非线性次数之间的关系[3-4，8]。

注意到式(4)中除系数为ai1，i2，…，ir的项之外，其余各项在Si1，i2，…，ir上模2求和结果均为0，因此，有

(6)

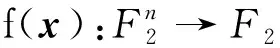
ai1，i2，…，ir=2r×2-nWH(f)(mod 2)=2r-n+mk0(mod 2) ，

这里WH(f)=2mk0(由引理2可知)。所以，当r>n-m时，ai1，i2，…，ir=0。当r=n-m时，若k0为奇数，则所有的n-m次项都出现；若k0为偶数，则所有的n-m次项都不出现。

当WH(f)=2n-1，m≤n-2时，可知k0为偶数。于是对于r≥n-m，都有ai1，i2，…，ir=0。

3.3 相关免疫阶与非线性度之间的关系

非线性度是衡量布尔函数的非线性程度的一个重要指标，它刻画了一个布尔函数和线性布尔函数类之间的符合程度，其精确定义如下。

为布尔函数f的非线性度。其中，dH(f(x)，l(x))表示f(x)与l(x)之间的汉明距离，即

对于二元域，有dH(f(x)，l(x))=WH(f+l)。

下面的定理给出了布尔函数的非线性度的沃尔什谱表示。

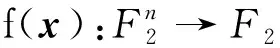
(7)

式(7)表明，布尔函数f的非线性度与f的最大绝对谱值有关。同时，也说明了f的谱值实质上反映了该函数与线性函数之间的符合程度，亦即非线性程度。

定理1中的式(3)可改写为

(8)

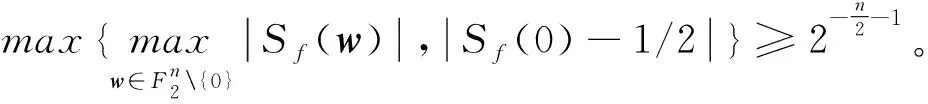
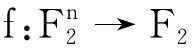
则

(9)

式(9)可由式(7)和式(8)直接推出。式(9)表明，Nf越大，NSf就越小；反之亦然。说明Nf和NSf之间存在着一种制约关系。从这里也不难看出，一个布尔函数的谱值中零值过多，必将导致其非线性度下降，故而从密码学角度来看，不是理想的函数。因此，在设计密码函数时要注意到这一点。

下面说明布尔函数的相关免疫阶和非线性度之间的关系[5]。

由定理2和式(9)易知，f(x)的相关免疫阶m和其非线性度Nf之间有如下关系：

(10)

式(10)可改写为

(11)

式(11)表明，m与Nf之间存在某种制约关系，相关免疫阶m对非线性度Nf的影响较大。在具体应用时，应适当折中。还可以给出一个更精细的关系[5]。

4 总 结

文中主要浅析了Xiao-Massey定理的意义和作用。这一定理为频谱技术在密码学中的应用开辟了一条广阔的道路，充分证明频谱技术是研究相关免疫函数的强有力工具。文中仅仅列举了3个方面的作用，关于Xiao-Massey定理的作用远不止这些。

5 跋

为了真诚地纪念我的导师肖国镇先生，我重温了Xiao-Massey定理。通过回忆肖老师当时对我的教诲和指导，梳理出此文。我认为这是对肖老师最好的纪念和思念。

曾有人讲过，一个人的生命主要由三部分组成：一是自然生命，这一点大家比较容易理解；二是亲戚朋友的生命，也就是说，只要他的亲戚朋友还在世，有人就会不时地提起他，惦记他；三是比较亲近的晚辈的生命，比如弟子、徒弟等也会不时地想起他，思念他。当这些人都已不在世时，这个人的生命也就真正结束了。我想肖老师不止这些，至少还有Xiao-Massey定理，他会永远活在密码人的心中。