2020年北京卷解几题的推广

湖南省桃江县第一中学 (413400) 胡芳举

本文将给出该题的两个推广.

图1

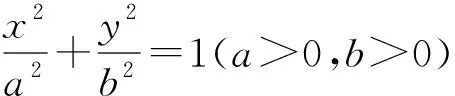
证明：当直线MN与x轴重合时容易验证结论成立.

由根与系数的关系知上式成立,故AB=BC.

注:AB=BC⟺kPM+kPN=2kPB.

图2

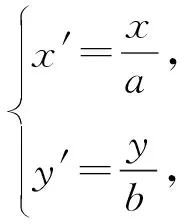
如图2,已知点Q与直线l是⊙O的一对极点、极线,直线OQ交l于点B,过点B作直线交⊙O于点M,N,再在过点Q与l平行的直线上任取一点P，设直线PM,PN分别交直线l于A,C,则AB=BC.

下面给出该结论的证明：