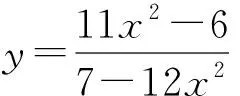2020年上海春考反函数压轴题引发的思考
2021-01-28华东师范大学数学科学学院200241武汉大学数学与统计学院430072周照杰
华东师范大学数学科学学院 (200241) 李 洋 武汉大学数学与统计学院 (430072) 周照杰
反函数是上海高中教材中比较重要的一个知识点,也经常出现在上海高考的压轴题位置.本文对2020年上海春考数学试题第12题进行展开,分析y=f(x)与其反函数y=f-1(x)的图象交点个数与交点位置问题,并在此基础上讨论高中阶段比较重要的两类函数指数函数y=ax(a>0且a≠1)与其反函数对数函数y=logax的图象交点问题.
1 试题呈现

评析:纵观近几年上海高考数学试题,小题的压轴题经常涉及对学生分析与转化问题能力的考查.第12题和第16题一般以动静结合的题目为多,常考查基本图形的平移、旋转、翻折等基本运动形式,这就需要学生把握好运动过程中的临界情况(即静止状态).本题作为压轴题呈现,考察原函数与反函数所组成方程的解的问题,要是直接代数求解,无疑增加了问题的运算且难以处理.这就需要我们熟悉原函数与反函数的一些基本性质.
2 基本性质
引理1y=f(x)与其反函数y=f-1(x)的图象关于直线y=x对称.
引理2 若y=f(x+a)存在反函数,则其反函数为y=f-1(x)-a(有兴趣的读者可以查阅2009年上海高考数学试题(理科)第22题).
性质1 若y=f(x)在其定义域上为连续函数,则y=f(x)与其反函数y=f-1(x)的图象存在交点的充要条件是y=f(x)的图象与直线y=x有交点.
证明:(充分性)充分性是显然的,下面我们证明必要性.
(必要性)设点P(a,b)是y=f(x)与y=f-1(x)的图象的交点.①若a=b,则命题显然成立.②若a≠b,则由点P(a,b)在y=f-1(x)的图象上知点P′(b,a)在y=f(x)的图象上,所以f(a)=b、f(b)=a.令g(x)=f(x)-x,则为连续函数,不妨设a
性质2 若y=f(x)为单调递增函数,且与其反函数y=f-1(x)图象相交,则其交点一定在直线y=x上.
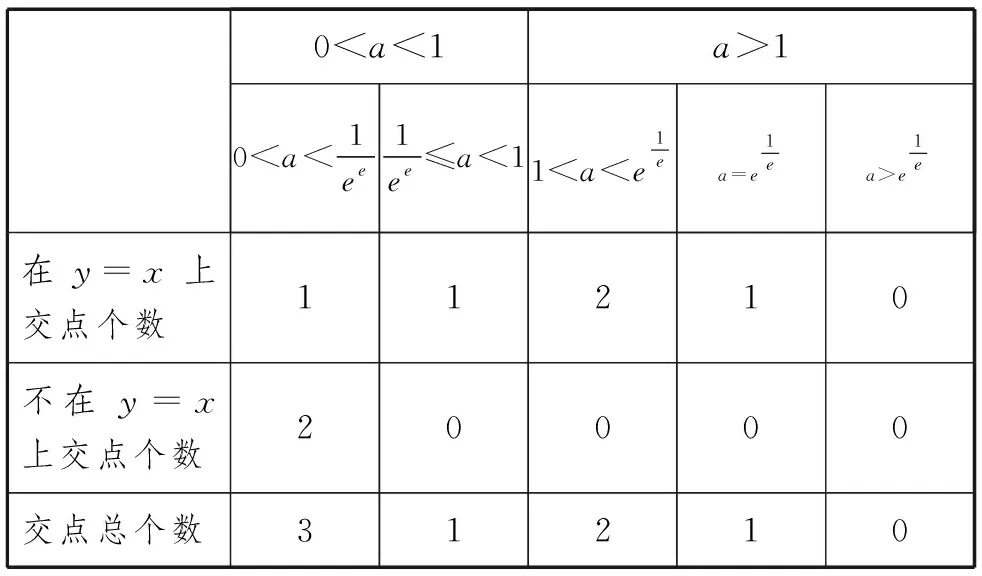
证明:(反证法)假设y=f(x)与y=f-1(x)的图象的交点P(a,b)不在直线y=x上,则a≠b,不妨设a 利用上面性质,我们回到例1的解答. 性质3 若y=f(x)为单调递减函数,且与其反函数y=f-1(x)图象相交,则交点不一定在直线y=x上.具体地说,在y=x上的交点至多只有一个,若在y=x外有交点,则成对出现且关于直线y=x对称. 推论若y=f(x)为单调递减的连续函数,且与其反函数y=f-1(x)图象相交,则在直线y=x上的交点有且只有一个. 证明:结合性质1和性质3可以直接证明. 指数函数y=ax(a>0且a≠1)与对数函数y=logax是互为反函数的一对函数,在我们常见的图象中,它们一般如图1所示.当0 (1)0 A.PB.QC.MD.N 当0 我们先求函数y=ax与其反函数y=logax相切时a的值. 当a>1时,指数函数y=ax在定义域R上是单调递增的.由性质2知,其交点一定在y=x上,这里只须考虑y=ax与y=x的交点问题. 综上,指数函数y=ax(a>0且a≠1)与反函数y=logax图象交点情况如表1. 表1 针对例1,笔者找到了两道类似的题目供大家思考. A.0 B.2 C.4 D.前三个答案都不对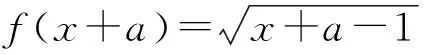
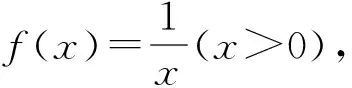
3 简单应用
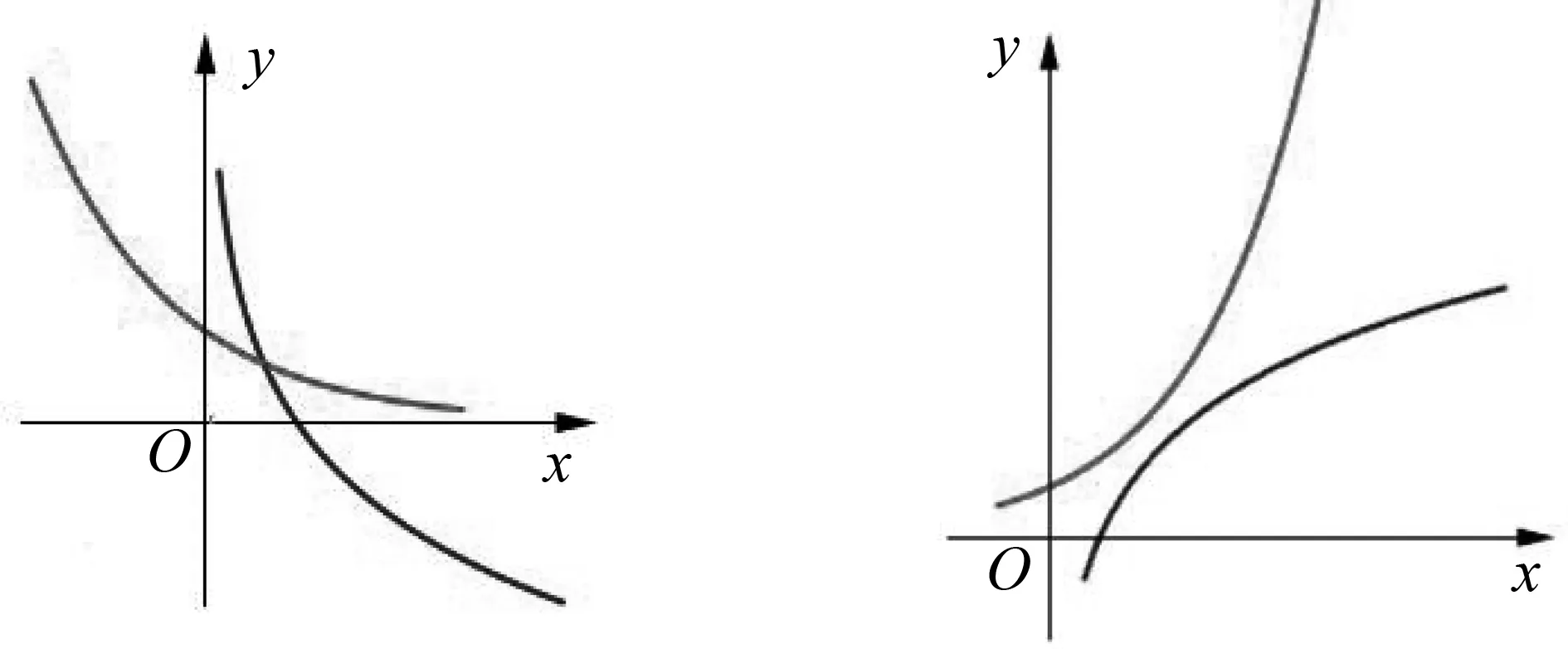


3.1 0

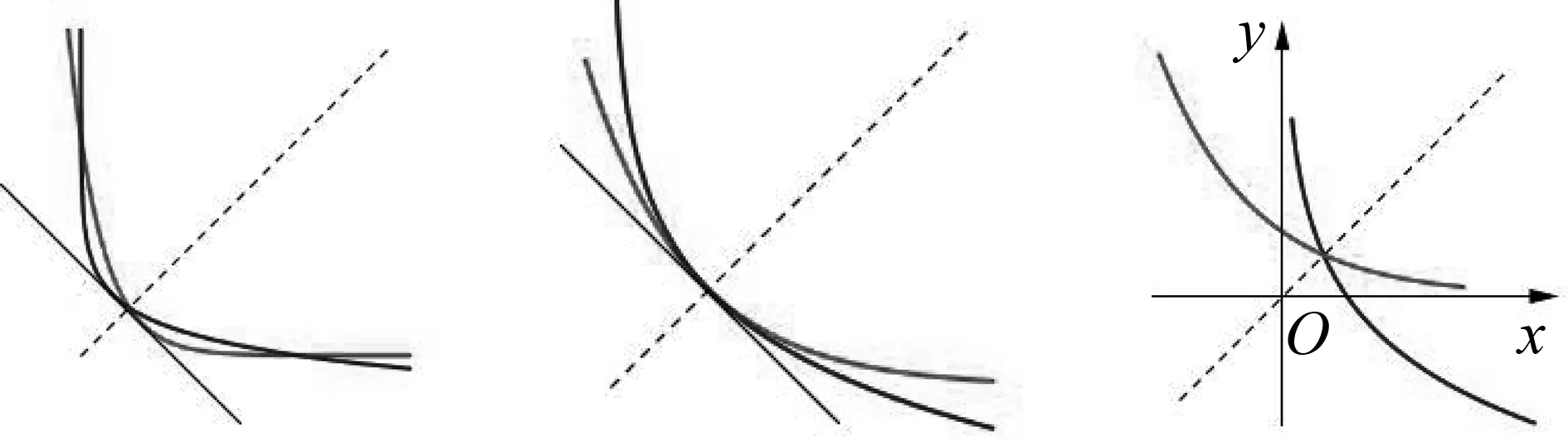
3.2 a>1时的交点问题


3.3 小结
4 类题训练