一类球面并联机构的速度与加速度分析

范 骏，杨随先，白青松

（四川大学制造科学与工程学院，四川 成都 610065）

1 引言

自1965 年Stewart 平台问世以来，并联机构（parallel mechanisms，PM）得到了学术领域和工业领域的广泛关注。相对于串联机构，其拥有诸如高精度、高速度、高刚度、低惯性和反向运动学求解简单等优点。在具有上述优点的基础上，球面并联机构（spherical parallel mechanisms，SPMs）的末端执行器还可以在一个球面上进行运动。目前典型的球面机构包括过约束和非过约束两种类型。前者如3-RRR（R 表示转动副）结构的the Agile eyes[1]；后者早期包括文献提出的 3-RRRRR 结构[2]，Di Gregorio 的 3-RRS（S 表示球面副）结构[3]等。上述球面并联机构具有移动或旋转奇异点，在此之后提出的结构在工作空间之内大都避开了奇异点，如双三角结构[4-5]等。球面并联机构广泛应用于包括指向设备、太阳能电池板、天线、航海模拟机构、内窥镜和摄像设备等方面[6]。而近来球面并联机构在医疗仿生领域的得到大量应用，如法国国家研究局（Agence Nationale de Recherche，ANR）主导了一系列将将球面并联机构应用于微创手术（minimally invasive surgery，MIS）的研究[7]，国内也有学者利用不同的球面并联机构对人体肩部关节进行仿生设计[8-9]。目前得到应用的球面并联机构以过约束为主，对加工和装配的精度要求极高。因此，提出一种对加工和精度要求不高并且计算简单的球面机构具有重大意义。

目前球面并联机构的运动学分析通常采用以下方法：利用几何约束建立由三角函数构成的约束方程，对约束方程进行求导从而推导出速度方程和加速度方程[10]；利用坐标系中各关节速度旋量之间的关系直接构造出速度公式或雅可比矩阵[11]261-264；直接根据末端执行器角速度和主被动关节变量的关系推导得出速度方程并再次求导分析加速度[12]4-6，[13]4-5；利用各分支端点运动空间的布尔运算求交集来得到运动平台即末端执行器的方向工作空间，并利用CAD 建模软件辅助分析，目前仅用于位置运动学[14]。

论文提出了一类新型三自由度球面并联机构，相比现有球面并联机构，其对于制造和装配精度要求较低，反向运动学求解更简单并且在工作空间中不含任何形式的奇异点。然后根据末端执行器角速度和主被动关节变量之间的关系，选择合适的关节向量构造了特殊向量来建立和简化了机构的速度和加速度模型，进而得到了运动雅可比矩阵并据此分析了机构的奇异性。最后，针对两种特定轨迹，根据速度和加速度模型利用Matlab 和ADAMS两款软件进行计算仿真得到了各分支主动关节角速度和角加速度变化曲线。

2 机构结构及其位置运动学

2.1 机构结构

图1 球面并联机构的基本结构Fig.1 Basic Structures of the SPMs

提出的一类三自由度球面并联机构的结构，如图1 所示。机架由三个互相固连的弧形滑动导轨条组成，其半径均相等，圆心位于同一点O，并且所在平面互相垂直。固定滑轨条上的交错滑块移动时，同时也带动移动弧形滑轨，弧形滑轨的半径也相同，圆心也落在O 点。移动与固定的滑轨在滑块处的切线保持垂直。移动滑轨的末端与末端执行器通过运动副相连接，根据连接方式不同分为三类：（1）通过转动副连接，记为3-PcPcR，其中，Pc—移动副在一条弧线上进行运动；R—转动副，此时三处转动副的轴线必须同时经过O 点；（2）先通过转动副，再通过万向节连接，记为3-PcPcRU，其中，U—万向节，此时对转动副的轴线方向没有要求；（3）通过球面副连接，记为3-PcPcS，S—球面副。其中，3-PcPcR 机构为过约束结构，虽然结构简单但对加工和装配精度要求极高，3-PcPcRU 和3-PcPcS 机构同为非过约束结构，对装配精度要求不高，但是球面副的加工精度和加工成本较高。三种机构具有相同的自由度（三个方向的转动自由度）以及相同的运动学模型。在末端执行器上安装Z 轴方向（Z 轴与末端执行器主平面垂直）的模组并带动加工刀具，根据安装的方向，机构可以对不同半径的内外球面进行加工，或者按照复杂的空间曲线轨迹行进。

以3-PcPcR 机构为例，其结构示意图，如图1（b）所示。在实际使用过程中，可以将原动机固定在滑块上利用齿轮啮合进行，并且在此基础上配合减速器使用可以进一步增加机构的负载能力。3-PcPcRU 机构的具体应用方案，如图2 所示。

图2 3-PcPcRU 机构的应用方案CAD 模型Fig.2 CAD Model of the Application Scheme of the 3-PcPcRU Mechanism

2.2 机构的位置运动学

机构的运动模型中需要用到的向量和角度，如图3 所示。O点到末端执行器连接点所形成的单位向量分别为t1，t2和t3，到末端执行器中心点的单位向量为te。其中，ti（i=1，2，3）之间的夹角记为δ，ti与te之间的夹角记为Δγ，这两个角度由加工制造确定。在保持当前方向te的前提下，末端执行器还可绕自身中心旋转Δθ。αi和βi分别是机构主、被动关节角度值。

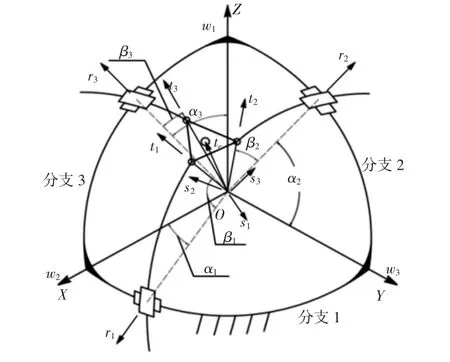
图3 运动模型中的向量与角度Fig.3 Vectors and Angles in the Kinematic Model

对于正向位置运动学问题，根据Euler-Rodrigues 参数写出ti关于主被动关节角度值的表达式，利用ti之间夹角一定的几何条件可以建立约束方程，对方程进行三角代换后利用Bezout 消元法可以得到一个16 阶多项式方程，找到唯一可行解后可以计算出对应的被动关节的角度值，进而得到ti的具体形式，其单位合向量即为te。而对于反向问题，根据te和Δθ 得到ti的具体形式，仅需对ti中部分元素进行反三角计算就可以得到主被动关节角度值。利用正向求解方法得到的3-PcPcR 机构工作空间，如图4 所示。为了简化计算，所有计算都将末端执行器的工作空间设定在一个单位球上，在不考虑干涉的条件下是一个八分之一球面。

3 机构的速度与奇异性分析

3.1 机构的速度分析

ti可认为是相应的坐标轴上的单位向量绕wi旋转αi至ri，再由ri绕si旋转βi的结果，其中αi为主动关节输入变量。对于球面并联机构，不需要讨论坐标系的移动而只需要讨论角速度和角加速度。

根据末端执行器的角速度向量和主被动关节变量导数的关系，有如下矩阵方程：

当 Δθ=0 时，使 τi同时垂直于 si与 ti。当 Δθ≠0 时，ti≠tmi，记τi＝tι×tmi，其中 tmi为在对应方位下当 Δθ=0 时 ti应处于的位置，其几何意义，如图5 所示。

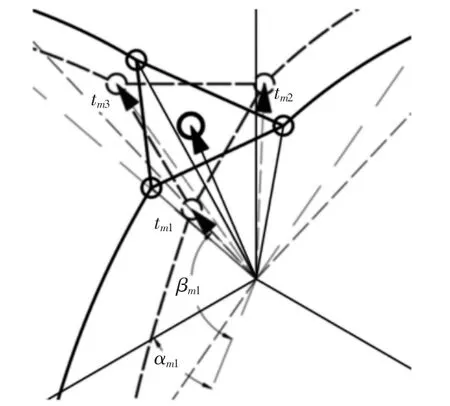
图5 tmi 的几何意义Fig.5 Geometrical Meaning of tmi

定义te基于各个分支的表达形式为tei和tmi，则每一组tei对应一组 αei和 βei。

为消除被动关节影响，在式（1）两边同时乘以（si×τi）T可得：

写成矩阵形式，有如下速度关系：

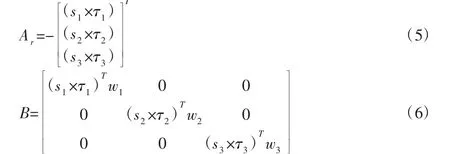
进而可以得到机构的运动雅可比矩阵：

需要注意的是，利用各关节速度旋量之间的几何关系，可以直接构造出基于速度旋量的速度方程。对于球面并联机构，只需要考虑旋量副部，同样可以得到形如式（4）～式（7）的速度方程和雅可比矩阵。这个方法在文献[11]中得到应用并且在文献[15]中得到总结。但利用旋量构造加速度方程在计算上有难度，并且在确定部分中间变量的值时需要用到上述过程中的向量，文献[11]利用这样的方法也仅仅讨论了机构的雅可比矩阵。因此论文采用与文献[12]和文献[13]中同样的方法如上文所示。

3.2 机构的奇异性分析

根据运动雅可比矩阵，并联机构的奇异性分为三类：

（1）B 缺秩：这种奇异性被称为第一类奇异性。在这种奇异构型之下，并联机构在工作空间中的一个或多个方向上失去了运动的能力，亦即驱动器在某一个方向上无法令运动平台产生位移。对应为几何意义为si，τi和wi必须共面，利用反证法进行证明：若Δθ≠0，则｛ti，si，wi｝或｛tmi，si，wi｝必须互相垂直。然而可证ti·wi≠0并且tmi·si≠0，条件相矛盾；若Δθ=0，则同样条件相矛盾。因此易知，对于涉及的球面并联机构第一类奇异点不存在。

（2）Ar缺秩：这种奇异性被称为第二类奇异性。在这种奇异构型下，并联机构在一个或者一个以上方向上运动不可控。从运动学的角度上说，存在一个非零的向量ts，使得当q˙α=0 时，有Arts=0（此时ts被称为Ar的零空间）。此时，机构在外部力旋量的作用下容易发生破坏。若Δθ≠0，此时Ar可以写成两个非零矩阵的乘积，因此；若 Δθ＝0，此时 Ar=-［t1，t2，t3］T一定保持满秩。因此，第二类奇异点也不会出现在此类机构中。

（3）Ar和B 同时缺秩，此类奇异性被称为第三类奇异性。此时并联机构在失去一个或一个以上方向上的运动能力的同时，在一个或一个以上的方向上运动不可控。对于涉及的并联机构，这一类奇异点也不会出现。

因此，在工作空间中，即 αi，βi∈（0，π/2）的范围内，机构不存在上述形式的奇异点。

4 机构的加速度分析

将式（1）对时间求导，可得：

为了消除非主动关节变量的二阶导数的影响，在式（8）左右两边同时左乘（si×τ）iT可消除被动关节二阶参数影响，并带入之前的结果：

其中，Ar和 B 的形式与式（4）中保持一致［c1c2c3］T，并且：

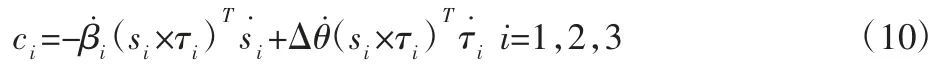
5 轨迹仿真

式（4）和式（9）所示的速度和加速度方程既可以用于利用驱动输入端的具体参数确定末端执行器的角速度和角加速度，也可以根据末端执行器角速度和角加速度特性反向求出相应的驱动输入参数。下面对与两种运行轨迹进行计算仿真，求出其角速度和角加速度运动特性曲线：（1）末端执行器与向量t0=［0.5773，0.5773，0.5774］T保持 π/12 的夹角和 Δθ＝0 以 π/5rad/s 的角速度旋转一圈，此时末端执行器的中点的轨迹为一个圆形；（2）末端执行器的欧拉角以如下运动形式变化其中t 表示时间，此时末端执行器中点的轨迹为一个空间二次曲线。同时，将制造确定的角度δ 设定为π/18，此时Δγ≈0.1008。对于结构简图，如图1 所示。在利用虚拟样机软件ADAMS 进行仿真时不便添加和分析运动副，因此需要建立一个等效机构，如图6 所示。其中所有的直线状的连杆仅为辅助添加运动副和测量组件的等效连杆。

图6 仿真等效机构Fig.6 Simulation Equivalent Mechanism

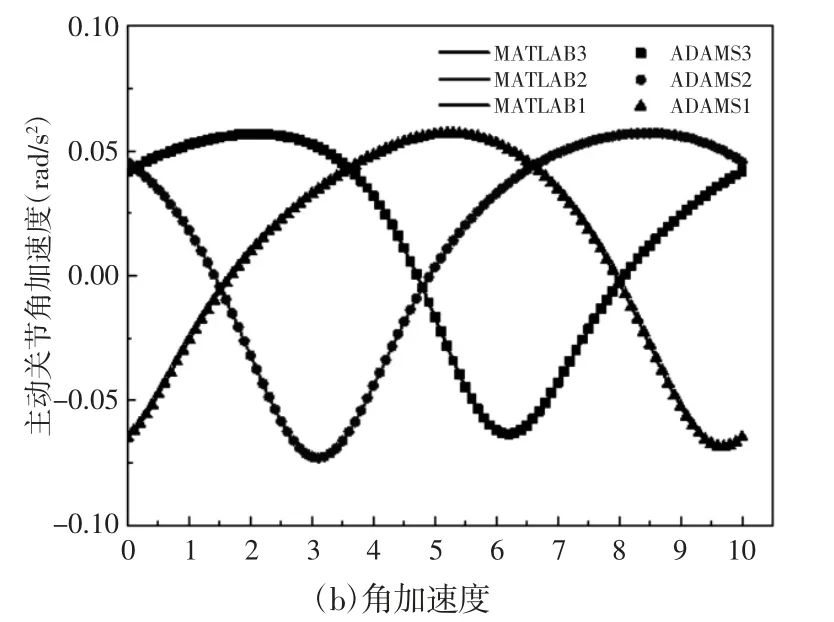
图7 轨迹（1）下主动关节变化曲线Fig.7 Active Joint Curves under Track 1

轨迹（1）的主动关节角速度与角加速度变化，如图7 所示。MATLAB1-3 和ADAMS1-3 分别表示主动关节1～3 的计算结果和仿真数据，用实线和离散点加以区分。保持Δθ＝0，则机构的速度与加速度分析和计算较为简单。

轨迹（2）中，Δθ 持续变化且可能出现 Δθ＝0 的情况，末端执行器可自转，此时主动关节角速度和角加速度，如图8 所示。通过比较，ADMAS 的验证结果与MATLAB 的计算结果相比，速度误差极小。值得注意的是在Δθ＝0 附近，角加速度可能会产生突变。

图8 轨迹（2）下主动关节变化曲线Fig.8 Active Joint Curves under Track 2

6 结论

（1）提出了一类具有相同运动学模型的三自由度新型球面并联机构，涵盖过约束和非过约束两种类型，其在工作空间之内没有任何形式的奇异点。

（2）根据末端执行器角速度和主被动关节变量之间的关系，利用关节向量构造特殊向量，简化了机构速度分析模型的建立，并简便地获得了机构的雅可比矩阵并分析了机构的奇异性，结合约束条件对速度模型进行求导进一步得到了机构的加速度模型。

（3）根据机构的速度和加速度模型，对于两种特定的轨迹进行了分析计算和机构仿真，给出了机构各分支主动关节角速度和角加速度变化曲线，对速度和加速度模型进行了验证。