基于改进的可拓神经网络的人防工程空气质量评估方法的研究
2021-01-27王体春张祥坤
王体春,张祥坤
(南京航空航天大学机电学院,江苏 南京 210016)
1 引言
人防工程作为特殊时期人员掩蔽场所,对于空气质量有较高的要求,这就要求在工程内部空气质量较差时,及时进行通风处理。人防工程通风模式分为清洁式通风、滤毒式通风和隔绝式通风三种[1]。而使用哪种通风模式,或者这三种模式在什么情况下进行转换,所依据的就是空气质量评估结果。
目前,空气质量评估方法种类众多[2-3],主要有综合指数评估法、模糊评估法、BP 神经网络评估法等等。但是由于人们对人防工程的关注度不高,所以关于人防工程空气质量评估方法还比较少。文献[4]探讨使用空气质量综合指数评估方法对空气质量进行评估,但该方法计算模式固定,只是计算污染物浓度与对应的《环境空气质量标准》规定的二级标准值之商的总和,当某种污染物浓度较高时,不能准确反映空气质量状况;文献[5]使用灰色聚类及模糊评估方法对空气质量进行评估,但此计算过程复杂,计算结果符合度还有待提高;文献[6]使用BP 神经网络对空气质量进行评估,该方法准确度较高但由于BP 神经网络神经元层数以及连接权数量较多,存在网络结构复杂、训练周期长的问题。
灰色管理聚类分析法可以用来研究“贫信息、小样本”的不确定性问题,在污染物种类不完全明确的时候,能够对已知污染物信息进行分析,发掘污染物之间隐含的关系[7-8]。相比于BP 神经网络,可拓神经网络仅有两层神经元结构,在运算效率上更具优势,并且也克服了BP 神经网络训练时间长、容易陷入非要求局限极值的缺点。可拓神经网络非常适合用于研究区间分类问题,这为研究空气质量级别划分提供了新的解决方案[9-10]。将人防工程空气污染物为研究对象,对基于灰色聚类和可拓神经网络相融合的空气质量评估方法进行了研究。使用灰色聚类原理依据空气污染物关联度对其进行分类并选取代表元素,然后使用可拓神经网络空气质量评估模型完成对空气质量的评估,并结合实例验证灰色聚类与可拓神经网络在人防工程空气质量评估中的可靠性和高效性。
2 人防工程空气质量评估模型的构建
2.1 融合灰色聚类的人防工程空气质量评估可拓神经网络模型
人防工程内部空气污染物成分比较复杂,影响因素众多。具体来说,空气污染物的成分及含量与人防工程的作用、所处位置、装修状况、管理维护效果、使用时长等有密切联系。比如:作为民用地下停车场使用的人防项目,其空气污染物主要为一氧化碳、二氧化碳、氮氧化合物等;地下商场、地铁站等人员密集的人防工程中,二氧化碳、挥发性有机物、菌类等空气污染物含量较高;装修时间较短的人防工程,空气会有甲醛、苯等污染物的出现。
研究的对象为人员掩蔽型人防工程项目,根据GB/T18883-2002《室内空气质量标准》[16]规定,选取人防工程代表性的二氧化碳、一氧化碳、甲醛、挥发性有机物、氨、苯、氡气七种空气污染物作为空气质量评估因子。使用防护工程空气质量综合监测仪对空气污染物进行实时监测。借助网络层,该设备能够将检测到的数据发送至云端服务器,以便应用层完成对数据的处理和保存工作。

表1 防护工程空气质量综合监测仪的设备性能参数Tab.1 Equipment Performance Parameters of Protective Engineering Air Quality Integrated Monitor
人防工程空气质量评估模型,在可拓神经网络结构的基础上融合了灰色聚类理论,灰色聚类分析能够简化可拓神经网络的结构,减少可拓神经元以及连接权的数量,融合灰色聚类后的空气质量可拓神经网络结构,如图1 所示。

图1 灰色聚类-可拓神经网络空气质量评估模型结构Fig.1 Grey Clustering-Extension Neural Network Air Quality Assessment Model Structure
灰色关联聚类对已知污染物信息发掘其隐含关系的过程是一个无监督学习的过程,在空气污染物种类不完全明确的时候,对空气污染物进行聚类时可以不需要任何先验知识,通过对样本数据进行数据特征提取、关联度计算、聚类划分等操作完成对样本数据分类。利用灰色关联聚类分析将空气污染物依照其内部关联性分为若干类,然后从每一类污染物中选取一个样本代表本类输入到可拓神经网络模型中对空气质量进行评估。
可拓神经网络将可拓学对事物的描述方法与神经网络的并行计算、学习能力结合到一起,在处理区间分类、识别等问题方面有较大优势。空气质量评估可拓神经网络模型采用有监督学习的过程,使用结果已知的数据对构建好的模型进行训练,在不断反馈、调整的学习过程中,空气质量评估模型与数据样本的契合度越来越高,当训练模型收敛时,训练过程结束,经过测试符合要求后便可用于空气质量评估中。
2.2 空气污染物初始序列建立与规范化处理
现假设从人防工程空气污染物数据库中提取m 个数据样本,每个样本存在n 种空气污染物元素,样本数据表示为:

式中:i,j—整数,分别表示数据中第i 个样本,样本中第j 个元素。
由于不同种类的空气污染物的描述单位不同,因此在含量数值上,不同污染物之间具有较大的差异。为避免因量纲的不同造成数据差别较大,在进行空气污染物关联聚类运算之前,需要对不同量纲的数据进行归一化处理,采用的归一化方法为minmax 归一化方法,如式(1)所示。

归一化处理后,所有数据的量值都会分布在[0,1]区间,方便后续的关联度计算以及可拓神经网络的收敛训练。然后再对样本数据进行始点零化处理:

然后以人防工程空气污染物类别为行、样本序号为列构建样本数据初始化矩阵,完成样本数据初始序列的建立与规范化处理。
2.3 空气污染物灰色聚类分析
空气污染物灰色聚类分析就是运用灰色关联理论来计算空气污染物之间的关联度,然后根据关联度的大小对空气污染物进行聚合分类。空气污染物灰色聚类分析的第一步是要计算空气污染物a、b 之间的绝对关联度εab:

式中:a=1,2,…,m,表示污染物类别。
当a=b 时,表示a 和b 是同种污染物,故:

在式(4)中:

在求得全部的绝对关联度之后,依照绝对关联度下标构建空气污染物关联矩阵,如式(8)所示。关联矩阵中的元素数值表示空气污染物之间的联系大小,数值越大表示对应的污染物关联性越大。绝对关联度大小是对空气污染物进行聚类的依据。绝对关联度的值域分布于[0,1]区间,一般情况下,当绝对关联度值大于0.5 时,对应的空气污染物之间就存在正向关联性。

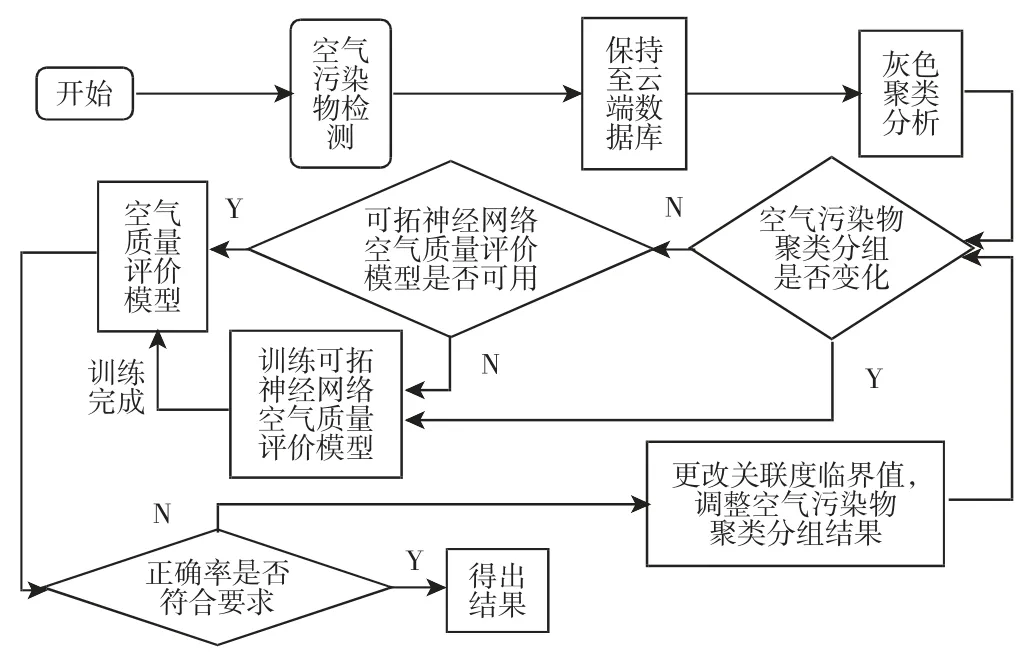
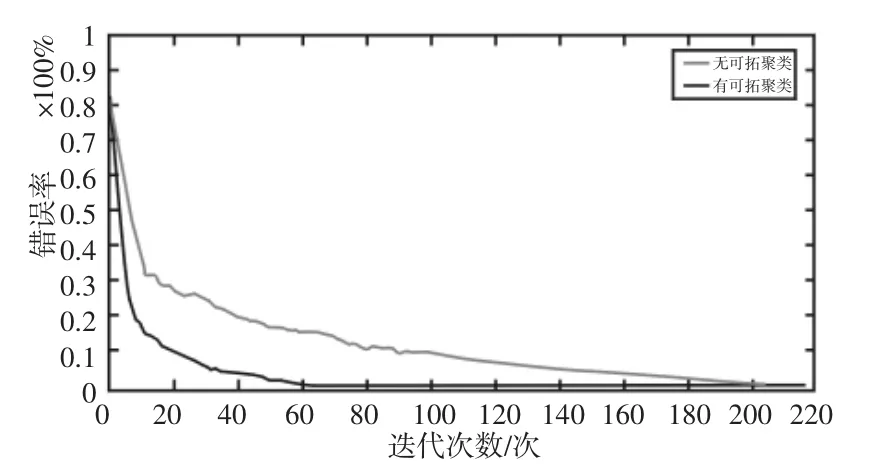
对空气污染物进行聚类,首先就是要确定关联度临界值r 的值,r 的取值范围一般为0.5 在根据实际需求确定r 值后,筛选出关联矩阵中的每一个大于r 值的元素,并将这些元素所对应的空气污染物做聚类处理,获得空气污染物的灰色聚类分析结果。然后计算每一类中所有空气污染物相对GB/T18883-2002 规定的标准含量的比例,选取每一类中相对含量最大的空气污染物代表本类参与空气质量评估过程。相对含量计算公式为式(9)所示,其中C0为标准值。 可拓神经网络只有两层结构,包括输入层与输出层。输入层神经元对应空气污染物物元的不同特征值,输出层神经元对应运算结果,在这里对应的是人防工程空气质量评估级别。输入层与输出层之间利用双权值进行连接,分别为对应特征经典域的上界和下界。例如,第i 个输入层神经元和第j 个输出层神经元之间的上界和下界可以用和表示。 可拓神经网络结构中的神经元被称为可拓神经元,它是组成可拓神经网络的基本结构。可拓神元有多个参数输入和一个结果输出,每一个输入参数都是一个物元变量,中间状态为输入信号的经典域的上界和下界表示,输出结果 y,如式(10)所示。 图2 可拓神经元结构Fig.2 Extension Neuron Structure 空气质量评估其实质也是区间分类问题,可拓距是可拓神经网络中一个重要的衡量工具,就是用来描述待测物体与目标区间中心的距离。在空气质量评估中用来描述空气污染程度与目标空气质量区间的符合程度。对于某一个区间 由可拓距离表达式可以看出:无论是从哪个方向,当点x 趋近于区间 图3 可拓距函数图像Fig.3 Extension Function Image 根据是否存在外部训练数据,双权连接的可拓神经网络可以分为有监督学习神经网络和无监督学习神经网络,这里使用有监督学习神经网络。有监督学习神经网络的训练过程,即利用若干结果已知的样本数据调节网络训练学习参数,使输出结果与目标结果相符的过程。 假设有空气质量已知的空气污染物样本集合X={X1,X2,,其中Np为空气污染物样本数量,则第i 条空气污染物样本数据表示为,其中n 为经过聚类分析简化以后的空气污染物数量,整个集合的学习误差表示为Er=Nm/Np,其中Nm为总的训练错误数。具体的过程为: 首先建立空气污染物可拓物元模型用以表示可拓神经网络输入节点和输出节点权值。 其次计算每种空气质量对应的空气污染物物元模型中的空气污染物量值区间的初始中心。 式中:k—空气质量对应的空气污染物物元模型,k=1,2,…,n。i—物元模型中的空气污染物类别i=1,2,…,nc。 如果有k*=p,使得EDik*=min{EDik},则按照如上过程进行下一次训练,直到完成所有模式的训练,否则更新权值和聚类中心后重新训练。权值和聚类中心的调整方法如下所示。 更新第p 个空气污染物样本和k*的权值: 式中:η—学习效率。 更新第p 个空气污染物样本和k*的聚类中心。 最后如果聚类过程收敛并且总误差符合要求,那么训练完成,否则重复训练过程重新进行训练。 人防工程空气质量评估的实现过程:首先,利用空气污染物检测传感器检测空气污染物含量,同时将测量值上传至云端数据库保存;然后使用灰色聚类理论依据空气污染物之间关联度的大小对空气污染物进行分类,并将聚类处理的数据传入空气质量评估可拓神经网络模型中,对模型进行训练;最后将检测到的空气污染物传入训练完成的空气质量评估模型便可得到空气质量评估结果。人防工程空气质量评估模型框架,如图4 所示。 图4 人防工程空气质量评估模型算法求解过程Fig.4 The Solving Process of an Air Defense Engineering Air Quality Assessment Model’s Algorithm 在人防工程空气质量监测数据库中,随机抽取不同时间、不同测量地点的10 条测量数据,研究不同污染物之间内在关联关系,如表2 所示。 表2 某人防工程空气成分监测结果Tab.2 Monitoring Result about Air Composition of an Air Defense Engineering 首先,提取数据,并依据式(1)对数据进行归一化处理。依据式(2)、式(3)对空气污染物矩阵进行始点零化处理。然后,依据式(6)、式(7)求解 Sa,a=1,2,3,…,m。再根据式(4)、式(5)、式(8),可求得关联矩阵A 为: 最后,依据样本间的关联程度对样本进行分类。为保证样样本间具有较高的关联度,关联度临界值r 应该大于0.6,但是r 值越大,样本分类就越多,输入可拓神经网络中的特征向量及连接权数量就越多,可拓神经网络就复杂,计算量就越大。所以r 关联度临界值r 的选取原则为:在能满足可拓神经网络运算准确度的同时,r 值越小越好。 根据相关经验,此处选取关联度临界值r=0.7,若最终空气质量评估结果准确度不符合要求再做调整。可以发现ε41、ε53、ε63、ε73、ε65、ε75、ε67的关联程度较为紧密,也就是 X4与 X1属于同一类,X3、X5、X6、X7属于同一类,X2为一类。这七种污染物指标的聚类结果为{CO2、TVOC},{甲醛、氨、苯、氡气},{CO}。经由查阅资料可以知道,空气中的CO2和挥发性有机物与人防工程中的人员活动有关;甲醛、氨、苯、氡大多来源于工程装修以及家具等散发的污染物;CO 有可能是来自于工程外部,汽车尾气排放产生的污染。 经过聚类分析以后,将七种污染物依照其关联性分为三类。每一类中的污染物可能来自于同一污染源,同类中污染物含量的增减具有关联性。因此后面评估空气质量时只需从不同类中各提取一个代表性污染物进行研究即可,这样可以在保证研究结果不失真的同时减少空气污染物监测成本以及相关工作量。 经过灰色关联聚类分析,七种空气污染物来源按照关联度可以分为人员活动相关、工程装修相关、工程外部侵入三类,现根据式(9)从每一类中各取一个指标,以CO2、CO、甲醛代表这三类空气污染物对空气质量进行分析。 在人防工程空气质量监测数据库中,按照优、良、轻度污染、中度污染、重度污染五种空气质量级别,对每个级别随机抽取100 条数据,并做归一化、规范化处理。相关数据,如表3 所示。 表3 某人防工程空气质量监测数据(部分)Tab.3 Monitoring Data about Air Composition of an Air Defense Engineering(Partial) 可拓学物元模型能够从物、物的特征、特征的值三个方面清晰的描述事物各项指标之间的关系和变化。使用物元理论构建以Om为对象,Cn为对象特征,Vn为特征量值的物元模型 Mm=(Om,Cn,Vn)。在该物元模型中,Om(m=1,2,…,5)为对应的五种空气质量状况;Cn(n=1,2,3)空气质量的影响因素,在此处表示CO2、CO、甲醛;Vn表示各影响因素对应的取值区间。空气质量评估物元模型,如表4 所示。 表4 空气质量评估物元模型Tab.4 Matter Element Model about Air Quality Assessment 图5 空气质量评估模型训练误差变化趋势Fig.5 Air Quality Assessment Model’s Training Error Trend 由空气质量评估模型训练误差变化趋势图可以看出,训练误差在初期急速下降,随着训练迭代次数的增加,训练误差逐步趋近于0。当训练迭代次数在65 次时,训练误差低至0.005 左右,可拓神经网络已完成收敛,训练过程结束。 表5 模型预测结果评定(部分)Tab.5 Evaluation of Model Predicted Result(Partial) 在可拓神经网络训练完成之后再从人防工程空气质量监测数据库中抽取100 条数据用作验证训练模型的准确性,新抽取的数据不包含之前的训练数据。对测试数据进行归一化处理后输入训练模型,其标定的空气质量和评估的空气质量,如表5 所示。可以看出,推算结果与标定结果相符,准确率达到98%,可以将该模型用于空气质量评估中。 若不使用灰色聚类理论对空气污染物进行聚类处理,将所有类别空气污染物都输入可拓神经网络空气质量评估模型对其进行训练,训练过程总误差变化趋势与使用灰色聚类理论的训练误差变化趋势对比,如图6 所示。 图6 灰色聚类的使用对提升模型训练效率的对比图Fig.6 Comparison of the Use of Grey Clustering to Improve the Misuse Efficiency of Model Training 由图6 可以看出,使用灰色聚类处理后的可拓神经网络空气质量评估模型在训练迭代次数达到65 次时就已经收敛,而不使用时,训练迭代次数在210 次时才完成收敛。详细对比情况,如表6 所示。与不使用灰色聚类相比,在空气质量评估准确度相差无几的情况,使用灰色聚类处理能大幅减少空气质量评估可拓神经网络模型中的神经元个数以及连接权数量,缩短训练时长,对模型运行效率上有较大提升。 表6 灰色聚类的使用对模型训练误效率的影响Tab.6 The Effect of the Use of Gray Clustering on the Mis-Efficiency of Model Training 主要工作如下:(1)研究使用可拓神经网络模型构建人防工程空气质量评估的方法。(2)引入灰色关联聚类理论,简化人防工程空气质量评估模型复杂程度,并对该理论引入前后的空气质量评估结果做出对比。 研究结果表明:①使用灰色关联聚类对空气污染物进行聚类预处理,能够减少输入可拓神经网络中的污染物种类数量以及可拓神经元连接权的数量,对可拓神经网络运算量的简化以及收敛速度的提升有明显效果。②关联度临界值r 对人防工程空气质量评估结果有影响作用,r 值越大,对模型的简化效果越小,空气质量评估准确度越高,反之亦然。在实验中可以不断调整r的大小,在能满足模型评估准确度的同时,r 值越小越好。 使用灰色关联聚类理论对人防工程空气质量评估模型进行优化,可以确保人防工程空气质量评估模型在保持较高评估准确度的同时提高模型的运算效率,对人防工程空气质量分析具有现实的意义。
2.4 空气质量可拓神经网络模型




2.5 空气质量可拓神经网络模型




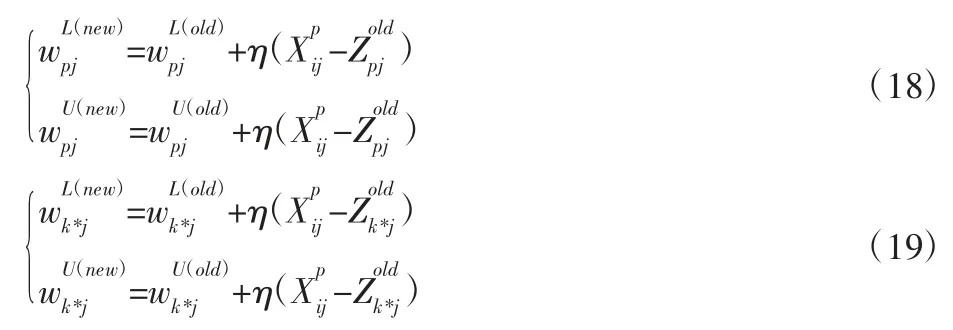

3 空气质量模型算法求解过程
4 人防工程空气质量评估案例
4.1 空气污染物的灰色关联聚类模型构建


4.2 可拓神经网络模式训练



4.3 人防工程空气质量评估模型测试


5 结论
