同时取送货的 “ 最后一公里 ” 车辆路径问题研究

袁雨果

（集美大学诚毅学院商船系，福建厦门361021）

一、引言

改革开放以来，我国经济社会的快速发展、经贸活动的不断增多，特别是电子商务的发展，为快递行业快速发展提供了良好的契机。国家统计局数据表明，2010—2019 年这10 年我国快递业务迅速发展，业务量增长26 倍，业务收入也相应地由574.6 亿元提升至7 498 亿元①，如图1 所示。一方面快递行业在增量市场（如农村快递业务） 仍旧大有可为，另一方面快递企业在存量市场上竞争却不断加剧。为了应对激烈的市场竞争环境，各快递企业都试图通过优化自身物流系统，以达到提升效率、降低成本和增强服务满意度的目标。近年来，客户退货维修或者物品回收等需求不断增加，一些快递企业也倾向于在进行 “ 最后一公里 ” 配送的同时揽收客户需要寄出的物件（如京东物流） 以提升物流服务效率，使得在 “ 最后一公里 ” 配送过程中整合正向物流和逆向物流成为企业提升运营效率和降低物流成本的重要途径[1]。

电子商务物流配送可以大致分为三个阶段，即仓储、主干网运输和 “ 最后一公里 ” 配送[2]，其中 “ 最后一公里 ” 配送是指将物品从仓储中心发送给终端客户的过程[3]。很多研究指出， “ 最后一公里 ” 配送极大地影响电商物流的服务质量和成本[2，4]，也是非常复杂的环节，因为它直接与终端客户接触，订单数量大而规模小，而且终端客户对配送方式、配送时间等要求都具有高度个性化和变动性等特点。

在此背景下，研究 “ 最后一公里 ” 车辆路径优化问题时考虑正向和逆向物流整合具有重要的意义。相比一般的 “ 最后一公里 ” 配送，本问题更为复杂，它包括两个交互影响的阶段：车辆配送和揽货任务的分配、车辆路径的优化。这个问题可以被抽象为一个同时取送货的带有时间窗的车辆路径规划问题（Vehicle routing problem with simultaneous pick-up and delivery with time windows（VRPSPDTW））。VRPSPD已经被广泛证明是一个NP 难问题，很难通过精确算法高效而准确地解决大规模VRPSPD[5]，而启发式方法则被认为是解决这类NP 难问题的有效方式。为此，结合遗传算法和变邻域搜索算法，设计了一个包括3 个步骤的启发式方法。通过构建100 个仿真场景，并通过统计分析的结果验证了该启发式方法具有较好的性能。

图1 2010—2019 年我国快递行业发展情况

二、文献综述

（一） “ 最后一公里 ” 物流问题

近年来我国电子商务快速发展，同时带动了快递等相关产业的发展。国家统计局数据表明，过去10 年快递业务量和业务收入年均增长率分别达到44%和33%①。然而，在电商物流快速发展的过程中也暴露出了一些问题，特别是 “ 最后一公里 ” 配送成为制约电商物流提升服务质量和降低物流成本的关键环节[6，7]。为了解决 “ 最后一公里 ” 配送存在的问题，一些创新的配送方式不断被设计出来，比如自助收发箱和顾客自提站等模式[8]：Mikko 等[9]和Song 等[10]的研究均表明，相比传统配送方式，在 “ 最后一公里 ” 配送环节中采用自助收发箱模式可以有效降低物流成本、提升配送效率。

尽管上述多元化的配送方式在一定程度上提升了电商物流 “ 最后一公里 ” 配送的效率，但是无法解决车辆回程空载所造成的成本问题。为了进一步降低 “ 最后一公里 ” 配送的成本，学界和业界都开始探索在 “ 最后一公里 ” 中整合正向物流和逆向物流，即考虑在进行配送的同时实现揽货。比如，郭月[11]分析了农村地区 “ 最后一公里 ” 配送和 “ 最初一公里 ” 揽收存在的主要问题，如需求量不足、配送成本高、设施不完善等，为此提出了 “ 选择取送货 ” 模式，从而为物流企业网点下沉提供有效的解决方案；何莹莹[12]针对家电行业中存在频繁的退换货从而导致逆向物流的现象，构建了考虑同时取送货的家电物流路径优化模型，并设计了混合粒子群算法进行求解。由此可见，同时考虑配送和揽收是传统 “ 最后一公里 ” 配送的变体，可以通过同时取送货的车辆路径问题进行建模。

（二） 同时取送货的车辆路径优化

车辆路径问题（Vehicle routing problem，VRP）最早由Dantzing 和Ramser[13]于1959 年提出，它是运筹学的一个热门研究问题。由于其应用的广泛性和在经济社会发展（如物流、交通等） 中的重要价值，国内外很多学者针对VRP 进行了大量的研究，并提出多种变体以更好地解决所研究的问题。这其中，Min[14]针对图书馆取送书任务的实际，在VRP 的基础上考虑同时取送货的问题，首次提出了VRPSPD。在此之后，很多学者开始尝试基于VRPSPD 解决物流和交通等领域的问题，比如：Liu[15]将VRPSPD 运用于家庭医疗物流优化中，并针对该问题构建了两个混合整数规划模型，同时提出了相应的解决算法；Shi[16]同样针对家庭医疗物流问题，提出了一种随机规划模型；Alshamrani[17]则将VRPSPD 运用于解决具有逆向物流的美国红十字会的血液配送问题，并提出了解决该问题的启发式算法。现有研究往往根据所解决问题的特征，对VRPSPD 做进一步拓展，形成一些新的变体，如：考虑车辆异质性（Heterogeneous VRPSPD）[18]、考虑车辆存在多个起止点的情况（Multi-depot-VRPSDP）[19]、考虑多层次配送问题（Multi-echelon VRPSPD）[20]、研究车辆行驶时间随机的情况（Stochastic travel-time VRPSPD）[21]和节点具有时间窗约束的情况（VRPSPD-time windows）[22]。同时，这些研究提出了大量的算法来求解VRPSPD相关的问题，如蚁群算法[23]、粒子群算法[24]、局部搜索算法[25]、遗传算法[26]、分支定界算法[27]、变邻域搜索算法（VNS）[28]、分支定界和离散萤火虫算法（DFA） 等[29]，以及将上述若干种算法相结合设计的启发式方法。

三、数学模型构建

整合正逆向物流的 “ 最后一公里 ” 车辆路径优化问题可以视为考虑同时取送货的带有时间窗的车辆路径问题（VRPSPDTW）。在保证该问题的主要特征的前提下，为突出主要问题特征而不失一般性，做出如下假定：1.所有车辆的起止节点都为同一个物流配送站点；2.一个客户可能只需要配送服务或只需要揽货服务，或两种服务同时需要；3.同一个客户有且仅有一台车辆服务；4.每台车辆都完全相同。为了便于问题的描述，表1 罗列了所涉及的变量及其相应的解释。

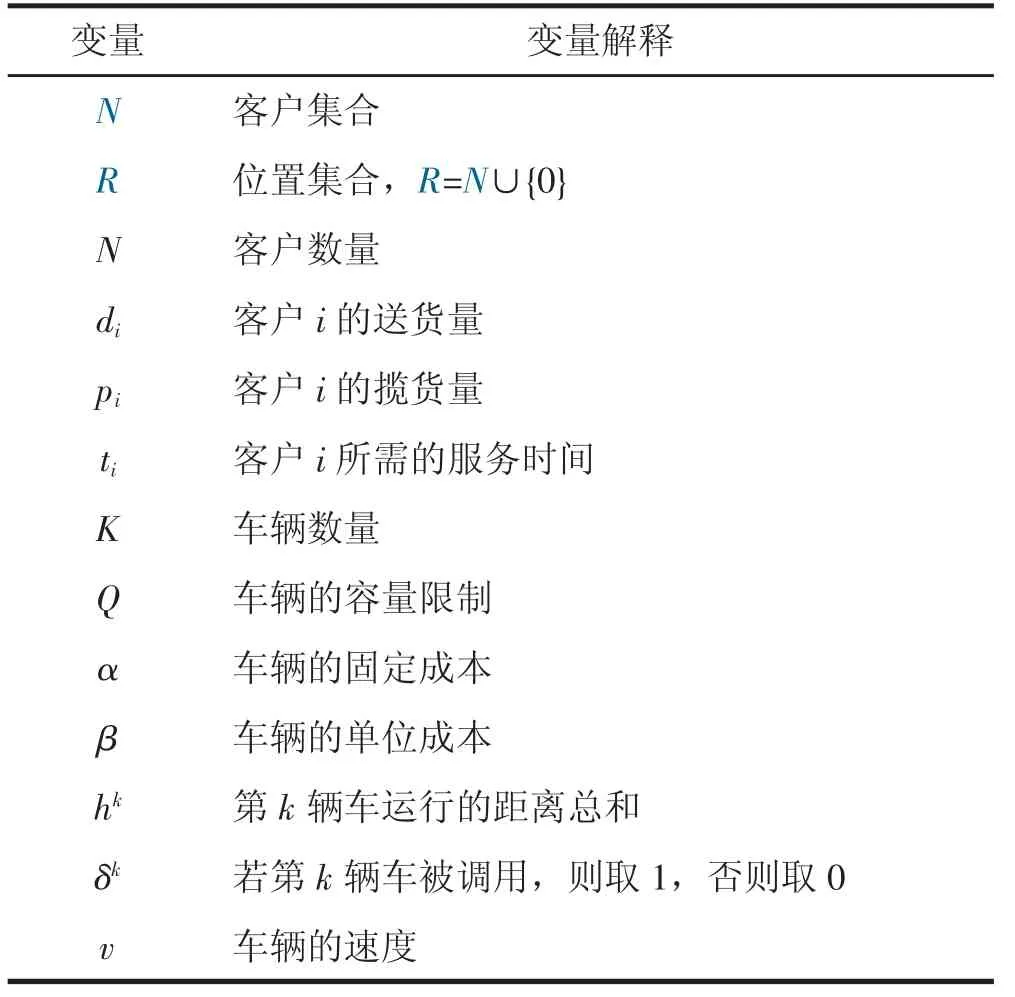
表1 变量定义及解释

（一） 目标函数

如果车辆k 从客户i 直接到客户j，则0-1 离散变量为1，否则则车辆k 行驶的总距离hk可以通过式（1） 计算，其中cij为客户i 与客户j 之间的空间距离。如果车辆k 被调用，则0-1 变量δk=1，否则δk=0，如式（2） 所示。本研究的目的是实现所有配送和揽收任务的总成本最低，如式（3） 所示，式中α 表示使用一台车辆的固定成本，而β 则表示每辆车单位距离所需要的变动成本。

（二） 约束条件

所有客户的配送或揽货需求都要被满足，且每个客户有且只有一台车辆服务，如式（4） 所示，其中N 表示客户位置集合，R 为所有位置集合（R=N∪{0}）。根据上述假设，所有车辆的起止点都为相同的物流站点，如式（5） 所示。式（6） 确保车辆空间路径的连通性，即车辆服务客户后需要离开该客户。所使用车辆的数量不能超过现有最大车辆数量K，如式（7） 所示。

青春如果没有了奋斗，没有了挣扎，没有了希望，没有了绝望，还叫什么青春？青春是一生当中最迷茫、焦虑、充斥着绝望、挑战的时候，但是为什么所有的人都说青春美好呢？

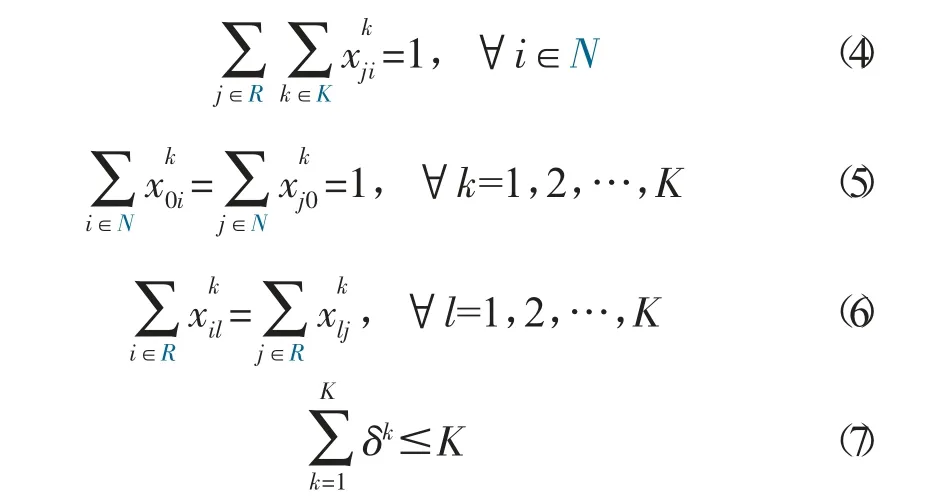
yij为经过弧（i，j）的客户i 之前的客户揽货总和，而zij为经过弧（i，j）的客户i 之后的客户货物配送总和。客户揽货和送货的情况分别如式（8） 和（9）所示，每辆车的载货量在任意时刻都不能超过车辆最大容量Q，如式（10） 所示。

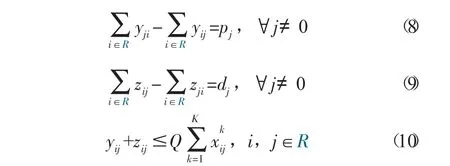
四、算法设计

VRPSPD 已经被广泛证明是一个NP 难问题，很难通过精确算法高效而准确地解决大规模VRPSPD[5]。为此，结合遗传算法和变邻域搜索算法，设计一个包括3 个步骤的启发式方法，该方法的流程图如图2 所示。

（一） 解编码

图2 算法流程图

根据表1 的定义，车辆数量为K、客户数量为N。在解编码过程中引入虚拟客户的概念来构建染色体，每条染色体代表一个解，具体处理如下：随机确定一个0～K-1 的整数作为虚拟客户的数量，则该问题可以转换为单车辆的路径优化问题，即车辆从物流中心出发，完成所有任务后，又回到同一物流中心。以图3 为例来说明解编码的过程，在该图中包括12 个客户，4 辆车。在0 到3 之间随机产生一个整数。假设随机产生的数为2，标记为13 和14。对客户集{1，2，…，13，14}排序，假定得到的一条染色体为0-3-4-7-9-13-10-1-2-5-14-8-6-11-12-0。将染色体中的虚拟客户（13 和14） 替换为物流配送中心0，即可得到0-3-4-7-9-0-10-1-2-5-0-8-6-11-12-0。以 “ 0 ” 为标记将该染色体进行拆分，得到{0-3-4-7-9-0}，{0-10-1-2-5-0}和{0-8-6-11-12-0}等3 条子染色体，分别表示3 辆车所分配的客户及线路。

图3 解编码过程（示例）

（二） 初始解集构造

根据上述解编码方式，可以构造大量解。然而，在构建过程中也可能会产生一些违反前述约束条件的解，可称为非可行解。为了提升后续解优化的效率，需要提前将非可行解删除，只允许可行解进入初始解集。初始解产生流程如下：

（1） 引入n 个虚拟客户（0≤n≤K-1），构建客户集合{v1，…，vN，vN+1，…，vN+n-1}；

（2） 基于（1） 得到的客户集，根据前一节假定生成一条染色体以表征一个解；

（3） 拆分（2） 中生成的染色体，以得到每辆车的服务客户及物流线路；

（4） 计算车辆完成所有任务所行驶的距离hk、整个过程中车载重量、服务每个客户的时间（5） 若该解为可行解，即满足各个约束条件，则将该染色体保存至初始解集合中，否则舍弃该染色体并重新返回步骤（1）；

（6） 如果初始解集合中包含的解数量达到算法预设的种群规模数量，则初始解集合构造的过程结束，否则返回步骤（1） 以生成新的解。

（三） 解集进化

解集进化是整个启发式方法的核心环节，为了提升方法的性能，根据本问题的特征，将进化过程分为两个阶段：全局优化和局部优化。遗传算法最早由Holland 在1975 年提出，由于具有较强的全局搜索能力等众多特点，遗传算法被广泛应用于解决车辆路径优化问题[26]。由Mladenovic＇和Hansen 提出的变邻域搜索算法通过系统地执行邻域变换程序以获得更好的解，它具有很好的局部搜索能力[30]。根据上述两种方法的特点以及本问题的特征，本启发式方法在全局优化中采用遗传算法，而局部优化则采用变邻域搜索算法。

1.全局优化

遗传算法包括交叉互换、变异和复制等算子，本启发式方法在进行全局优化时采用单点变异和双点变异两种算子。分别以图4 和图5 来说明单点变异和双点变异的过程。对于单点变异，首先从解集中随机选择一个解（如3-4-7-9-13-10-1-2-5-14-8-6-11-12），并从该染色体中随机选择一个基因（如图4 的 “ 1 ” ）。以该变异点为节点，将染色体截取为3-4-7-9-13-10 和2-5-14-8-6-11-12 两个染色体片段，并交换两个染色体片段的位置以形成新的染色体，即：2-5-14-8-6-11-12-1-3-4-7-9-13-10。

图4 单点交叉变异

染色体双点变异的过程如图5 所示，同样从解集中随机选择一条染色体（如2-5-14-8-6-11-12-1-3-4-7-9-13-10），并在该染色体中任意选择两个基因（如图5 的 “ 8 ” 和 “ 4 ” ）。以两个变异基因为节点将染色体截取为3 个片段：2-5-14，6-11-12-1-3 和7-9-13-10。其中，采用倒序的方式对两个变异基因间的片段进行重新排序，从而得到新染色体，即2-5-14-8-3-1-12-11-6-4-7-9-13-10。

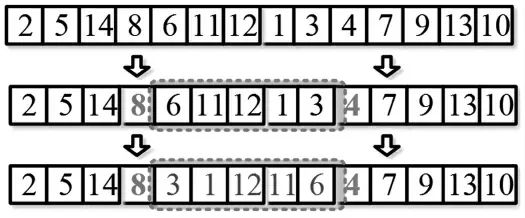
图5 两点交叉变异

2.局部优化

由于VNS 具有结构简单和鲁棒性较强等特点[31]，因此被广泛应用于VRP 的相关研究中[28]。VNS 系统地将邻域分为两个相互作用的阶段，变邻域下降阶段（VND） 的目的在于得到局部最优，而扰动阶段来跳出当前局部最优。这里，采用两种扰动策略来完成VNS 的扰动：1） 随机移动虚拟客户在染色体的位置，如图6（a） 所示。2） 调整虚拟客户的数量，如图6（b） 所示。具体而言，1） 当现有染色体的虚拟客户数量为K-1，则随机减少一个虚拟客户；2） 当现有染色体的虚拟客户数为0 时，则增加一个虚拟客户并随机插入到染色体的其中一个位置；3） 当现有虚拟客户的数量介于1 和K-2 之间，则随机增加或减少一个虚拟客户。VND 中依次包含的结 构 有Insert、Move-Best、Two-Opt、Swap-Best、Extract-Insert 和Extract2-insert[32]。

图6 两个VNS 扰动策略实例

在局部优化中基于上述2 个扰动策略和6 个邻域结构：首先产生一个初始解，并执行第1 个扰动策略以得到该初始解的扰动解，记为S（i）；针对该扰动解S（i），依次执行上述6 个邻域结构，不断优化该扰动解，直至找到局部最优解。如果找到的局部最优解优于S（i），则重复执行第1 个扰动策略，否则则执行第2 个扰动策略。重复上述过程，但所有扰动策略执行完毕后，则VNS 的过程结束，该过程将输出优化后的解。

五、算例分析及讨论

为了验证本方法的性能，通过模拟产生100 个仿真场景。具体而言，随机产生一组客户集合（包括客户的数量、客户的位置、客户取送货重量、客户的时间窗）、配送中心的位置以及车辆最大数量。同时，为便于比较，引入标准遗传算法作为比较基准。为了减少误差，对于每个仿真场景，都用两种算法分别运行30 次，并对这30 次结果取平均值（如图7）。

图7 两种算法总成本对比

为了探索两种方法的性能是否有统计学意义上的差异，使用配对样本t 检验的方法对二者的结果进行进一步分析。检验结果分别如表2 和表3 所示：遗传算法得到的总成本均值为978.74，标准偏差为271.30，而启发式方法得到的成本均值和标准偏差分别为823.82 和280.96，t（100）=23.90，p＜0.05，说明在0.05 的显著性水平下，相比于遗传算法，启发式方法得到的总成本显著较低。

表2 描述统计（遗传算法Vs.启发式方法）

表3 配对样本t 检验结果（遗传算法Vs.启发式方法）

六、研究总结与展望

近年来，我国电子商务的快速发展带动了快递行业的发展，相应地也加剧了该行业的竞争。 “ 最后一公里 ” 作为电子商务物流活动的最后环节，在提升物流效率、降低物流成本和提高服务满意度等方面具有重要意义；与此同时， “ 最后一公里 ” 同样也面临众多问题和挑战。

“ 最后一公里 ” 整合正逆向物流的车辆优化问题，被抽象为一个VRPSPDTW，设计一个基于遗传算法和变邻域搜索算法的3 步骤启发式方法来求解该问题。通过构建100 个仿真场景，并通过统计分析的结果验证了该启发式方法具有较好的性能。

尽管所设计的启发式方法能够较好地解决同时取送货的带有时间窗的车辆路径规划问题，但是随着客户规模的增加，算法的效率还有待提升。除此之外，由于交通拥挤、等待客户等情况时有发生，这就使得将交通时间和服务客户时间视为确定值往往与实际情况不符合。因此，未来在研究 “ 最后一公里 ” 物流车辆路径优化时，需要进一步考虑这些随机因素。

注释：

①数据来源：国家统计局.