基于差分理论的混凝土温度参数反演模型的GA算法研究
2021-01-27周超峰马跃先
杜 玮,周超峰,邓 旭,马跃先
(1. 河南省农村水电及电气化发展中心,郑州 450003; 2. 河南省陆浑水库管理局,河南 洛阳 471412;3. 河南郑大水利科技有限公司,郑州 450001; 4. 郑州大学水利科学与工程学院,郑州 450002)
0 引 言
大体积混凝土是现代工程中的重要结构形式,合理计算并确定混凝土的温度场及温度应力分布,是其温控施工控制的重要环节[1,2]。目前,大体积混凝土温度场及温度应力的计算包括经验公式法、差分算法以及有限单元法等[3,4],但上述计算均需要依靠混凝土的温度参数进行计算,而温度参数的获取主要通过经验计算或试验法获得,由于现场施工环境、测量设备、施工工艺的不同,导致获取的温度度参数与实际工程仍然存在一定的误差。
反演理论利用实测数据对计算参数进行修正,但针对混凝土温度参数的反演研究相对较少,笔者曾提出混凝土温度场、湿度场的差分计算模型[5,6],并针对混凝土湿度场的湿度扩散系数提出差分反演模型[7],但该模型的反演参数较少,模型较为简单,而混凝土温度参数较多,反演模型复杂,湿度场的反演模型和求解方法无法直接应用。
本文基于差分理论,构建混凝土温度场的差分计算模型,利用实测数据建立混凝土温度参数的差分反演模型,并针对反演模型,设计相应的遗传算法模型,通过对混凝土温度参数的反演计算,可以较为准确地获取符合实际工程的温度场参数,从而对大体积混凝土的温控提供指导。
1 混凝土温度场的差分计算模型
1.1 热传导方程
大体积混凝土的热传导方程可表达为[1]:
(1)
式中:c为混凝土比热,kJ/(kg·℃);λ为混凝土的导热系数,kJ/(m·d·℃);τ为时间,d;ρ为混凝土密度,kg/m3;θ为混凝土绝热温升;x,y,z为混凝土内部点的位置坐标;T为混凝土内部坐标点温度,℃。
1.2 初始条件和边界条件
对大体积混凝土的温度场进行求解时,需要确定其初始条件和边界条件。
初始条件:初始温度为其初始瞬时温度,即浇筑温度,为常数。
T(x,y,z,0)=T0=const
(2)
边界条件:根据混凝土的接触介质不同,其边界条件可以分为第一类边界条件~第四类边界条件,具体可参见文献[1,5];其中,第三类边界条件使用较多,其假定混凝土表面的热流量与其表面温度T和气温Tf之差成正比。即:
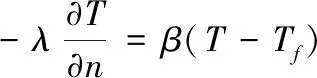
(3)
式中:β为混凝土表面的放热系数。
1.3 差分计算模型
对于上述构建的热传导方程,划分差分单元,建立其差分计算模型,其中计算模型,如图1所示,其中x方向格距为h,y方向格距为l,z方向格距为v,用中心差商代替微商。
温度场的差分计算模型可表示为:

(4)
(5)
(6)
代入式(1)得:
T0,τ+Δτ=(1-2r1-2r2-2r3)T0,τ+r1(T1,τ+T2,τ)+
r2(T3,τ+T4,τ)+r3(T5,τ+T6,τ)+Δθ
(7)
式中:r1=aΔτ/h2,r2=aΔτ/l2,r3=aΔτ/v2,Δθ=θ(τ+Δτ)-θ(τ),当r1+r2+r3<0.5时,计算结果稳定。
第三类边界条件的差分格式可利用牛顿后插公式,建立其差分格式为:
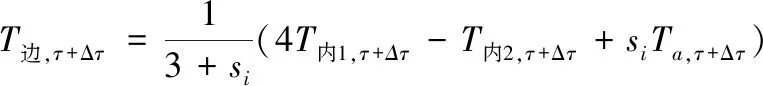
(8)
式中:T边为混凝土边界处温度;T内1为混凝土内部距离边界为1单位的节点的温度值;T内2混凝土内部距离边界为2单位的节点的温度值,对于x方向,取s1=2βh/λ,对于y方向,取s2=2βl/λ,对于z方向,取s3=2βv/λ;Ta为外界介质温度。
2 温度场实例分析
2.1 计算参数
针对某混凝土工程,为准确获取混凝土的温度参数,在实验室进行混凝土温控试验,选择50 cm×50 cm×50 cm的混凝土试块,在恒温恒湿养护箱内保持恒温(15 ℃)、恒湿(95%湿度)的工况下养护20 d,其中混凝土的各温度参数通过经验估算见表1。

表1 混凝土温度参数Tab.1 Temperature parameters of concrete
混凝土的绝热温升可以表示为:
Q(τ)=Q0(1-e-aτb)
(9)
式中:Q(τ)为龄期为τ时的累积水化热,kJ/kg;Q0为最终水化热,kJ/kg;τ为龄期;a,b为固定系数。
其中,混凝土的绝热温升可根据下式计算:

(10)
式中:W为每方混凝土中的水泥含量,kg/m3;F为每方混凝土中掺合料含量,kg/m3;k为折减系数,对于粉煤灰,可取0.25。
根据经验进行计算取值见表2。

表2 混凝土最终水化热及系数取值Tab.2 Final hydration heat and coefficient of concrete
为对混凝土试块的温度变化进行测量,设置温度传感器进行测量,所述温度传感器布置位置见图2。
2.2 温度场计算
根据本文构建的差分模型,对上述试件进行温度场差分计算,其中混凝土单元划分为5 cm,时间划分为0.002 d(即每隔2.88 min计算一次),计算周期为20 d,分别计算各测点的混凝土温度变化历时曲线见图3。
通过图3可知,混凝土各测点的温度先升高后降低,前期温升主要是由于水泥水化热产生的热量大于空气散热,后期水泥水化热产生的热量小于空气散热,则温度出现降低,并逐渐接近外界空气气温。对于各测点而言,越接近空气表面的测点,其受外界温度影响越剧烈,其温升越小。
为展现混凝土各点的温度分布情况,分别计算2、20 d后,混凝土的温度场分布云图,计算结果见图4、5。
由图4、5分析可知,混凝土的中心点温度最高,边界点的温度最低,且混凝土试件的四边角温度最低,主要是由于其同时受到两个空气扩散面的影响,其温度受外界空气温度最为剧烈。
2.3 温度误差分析
通过采集各测点的温度数据,每隔0.5 d提取一次数据,共提取20 d的40个温度数据,通过经验估算得到的温度计算数据与实测数据进行对比,其误差分析见图6、7。
通过图6、7分析可知,通过经验估算得到的温度计算数据与实测温度数据存在较大的误差,尤其前8 d的数据误差较大,最大误差接近1 ℃,而后期误差相对较小,主要是前期温升阶段,受混凝土温度参数的影响较大,如不合理确定温度参数,会导致理论计算与实际产生较大的偏差。
3 基于协同遗传进化的反演模型及求解
3.1 反演模型建立
为消除理论计算与实测数据的误差,基于实测数据,建立反演模型,考虑误差的正负变化,采用误差值的累积平方和作为反演目标函数值,其反演模型可以表达为:
(11)
式中:W为计算值与实测值的误差平方和;T为实测温度值;T′为理论计算值;m为测点个数;n为各测点的温度测量/计算的时段数;f为温度计算的差分函数;a1,a2,…,as为各温度参数,基于本例,可以选择为混凝土的导热系数、比热系数、密度、表面放热系数,绝热温升、经验指数a、经验指数b。
3.2 GA算法设计
上述反演模型为非线性多参数的复杂求解模型,无法利用理论计算求得其解析解,本文拟采用遗传仿生算法进行求解,设计其算法流程见图8。
其中,遗传参数种群包括混凝土各温度参数,适应度函数即为反演模型的 值,遗传规则可制定为:适应度函数值小的个体向下一代遗传进行,其中适应度函数值越小,其遗传概率更大;变异规则可制定为:每代种群中的变异个数取种群个数的10%,以避免遗传种群的局部收敛;进化代数作为遗传终止判别条件,终止后,对种群的所有历史解进行对比,寻找最小值,并输出该最小值对应的各种群值。
3.3 遗传反演求解
按照本文设计的遗传算法,进行反演模型求解,其中各温度参数种群规模设定为100,遗传代数为40代,其中各温度场参数的求解范围可确定见表3。

表3 温度参数的求解范围表Tab.3 Solution range table of temperature parameters
以导热系数和比热系数为例,种群规模选择确定其初始种群分布见图9、10。
遗传进化40代后的种群分布见图11、12。
遗传进化的适应度函数跟踪见图13。
4 反演结果及评价
4.1 反演结果
根据上述遗传算法进行反演求解,40代后,适应度函数最小值为1.236,确定最优种群的温度参数见表4。

表4 反演后的温度参数表Tab.4 Temperature parameter table after inversion
4.2 反演评价
利用反演后得到的参数进行温度场差分计算,得到其各测点的温度变化与实测值的历时过程线及误差分布见图14、15。
其中分别对反演前后2 d及20 d的温度误差场的分布对比见图16、17。
各测点的温度误差平方和比较见表5。
通过上述图表可知,经过反演后的温度参数经过差分计算,其计算温度值与实际温度值吻合度较好,各测点的温度误差平方和均下降75%以上,较大的消除了经验参数带来的误差。
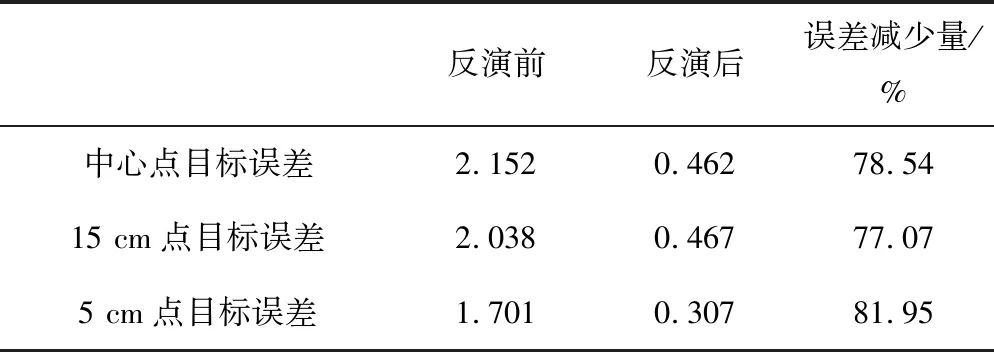
表5 各测点的温度误差平方和比较表Tab.5 Comparison table of sum of squared temperature error of measuring point
5 结 语
(1)通过温度场差分模型,可以对混凝土温度场进行仿真模拟,但温度参数对温度场的影响较大,仅依靠经验确定温度参数,误差较大;
(2)利用实测温度数据,可以建立混凝土温度参数的反演计算模型,该模型可以较好地修正经验参数,减少误差;
(3)GA算法可以较好地求解非线性多参数的优化问题,通过合理的适应度函数选择、遗传规则及变异规则制定,可以较好地求解混凝土温度参数的差分-反演模型。
□
