过程法模拟构建数字岩心

罗加荣

(上海勘察设计研究院集团有限公司，上海 200093)

1 引 言

数字岩心建模方法可分为：物理实验方法和数值重建方法。物理实验方法借助高倍光学显微镜、扫描电镜或CT成像仪等高精度仪器获取岩心的实际平面图像，然后依据这些扫描数据进行三维重建数字岩心，而不通过计算机模拟岩心的结构；数值重建方法则依据少量岩心平面图像数据，然后采用数学方法使用计算机模拟建立数字岩心[1,2]。

数字岩心建模的物理实验方法主要包括序列成像法、MRI核磁共振成像法、聚焦扫描法和CT扫描法等方法[3,4]。

数字岩心建模的数值重建法主要是采用基于薄片分析的图像构建法，包括高斯场扫描技术、模拟退火算法、多点统计法、马尔可夫随机法和过程法[5]，其中过程法是近年来新提出的构建数字岩心的数值方法，该方法主要通过模拟岩石形成的过程建立数字岩心[6]。由过程法构建的数字岩心，能提高对岩石沉积过程的认识，并为岩石孔隙度模拟计算研究提供参考。本文在模拟沉积过程时，采用已沉积的岩石膨胀曲面变化来判断下一个将沉积的岩石稳定位置，便于深入理解过程法构建数字岩心的关键过程。

2 过程法建模

过程法建立数字岩心是通过模拟岩石的沉积过程、压实过程和成岩过程的结果来建立数字岩心，沉积过程模拟确定颗粒的最终沉积位置[7]。

2.1 沉积过程模拟假设

岩石沉积由于受到颗粒形状和环境的影响，使得沉积过程相当复杂，为简便处理，做以下一些基本假设[8]：

1)单个岩石颗粒都视为微小球体，直径从粒度分布曲线选取；

2)沉积区域称为沉积盒，为规则长方体形状；

3)岩石初始位置中心坐标在沉积盒内随机；

4)岩石颗粒向重力势能下降最快的方向运动，并与已沉积在盒内的岩石颗粒不发生弹跳，且忽略岩石颗粒形变；

5)岩石颗粒到达相对稳定位置后，后续岩石颗粒才开始下降，并不对已稳定颗粒造成影响。

2.2 确定沉积颗粒直径

经统计分析，岩石颗粒直径服从粒径累积概率分布[9]，如图1所示。生成一个随机数(0，100)%，选择对应随机数的直径为岩石颗粒的直径。

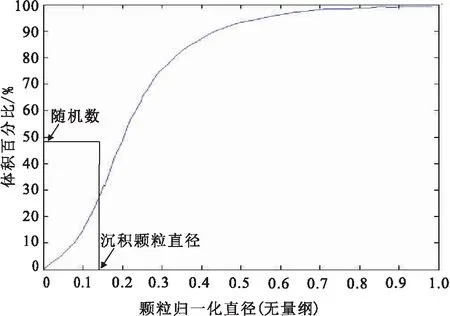
图1 粒度组成累积分布曲线

2.3 沉积过程模拟

利用数学方法对岩石颗粒沉积路径进行计算，判断岩石颗粒最终沉积的位置。为简化计算，模拟岩石沉积过程如下：

1)设定一个长方体(长、宽、厚)为沉积盒区域；

2)生成一个随机数(0，100)%，根据粒径累计概率分布获得沉积颗粒半径r；

3)假设即将沉积的颗粒半径为0，将所有已沉积在稳定位置的颗粒半径扩大r；

4)在已沉积区域和扩大区域以外的区域随机选取岩石颗粒初始下落位置；

5)选择重力势能下降最快的方向能到达的局部势能最小位置或全局势能最小位置作为本次沉积颗粒的稳定位置；

6)将当前颗粒半径设为r，其他所有颗粒的半径及沉积区域均恢复原大小；返回步骤2)。

沉积过程模拟如图2所示。

图2 沉积过程示意图

2.4 沉积过程编程实现

为了便于编程处理和实现，简化模型为了便于成图观察分析，进行初始化处理和做出以下假设：

1)沉积盒模型大小设为Xmax=60,Ymax=60,Z无上限；

2)颗粒半径变化范围为：1～10；

3)沉积颗粒个数设为：9 个和100个。

为了简化运算，将该岩石颗粒的后续沉积过程简化为其球心在已沉积岩石颗粒球面上的运动。在颗粒沿球面运动中，判断该颗粒是否已经达到其稳定位置，若为稳定位置，则终止该颗粒的沉积过程。

每次颗粒沉积时，随机获得颗粒半径，根据前面的已沉积颗粒信息即坐标和半径,找到膨胀曲面上距离颗粒下降方向最近的势能局部最小点，作为颗粒的局部稳定点[10]，即颗粒到达该位置后将不再继续滚动，岩石颗粒沉积实现流程如图3所示。

图3 沉积过程模拟流程

在每个颗粒沉积时，膨胀曲面都是变化的。9个颗粒沉积的膨胀曲面变化和沉积情况如图4所示。100个颗粒沉积时沉积情况如图5所示。

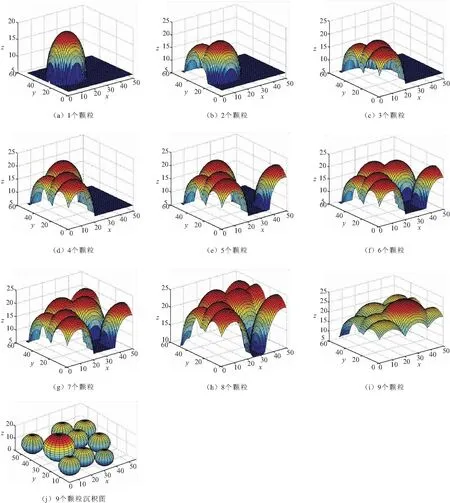
图4 不同个数沉积颗粒时膨胀曲面变化和沉积图

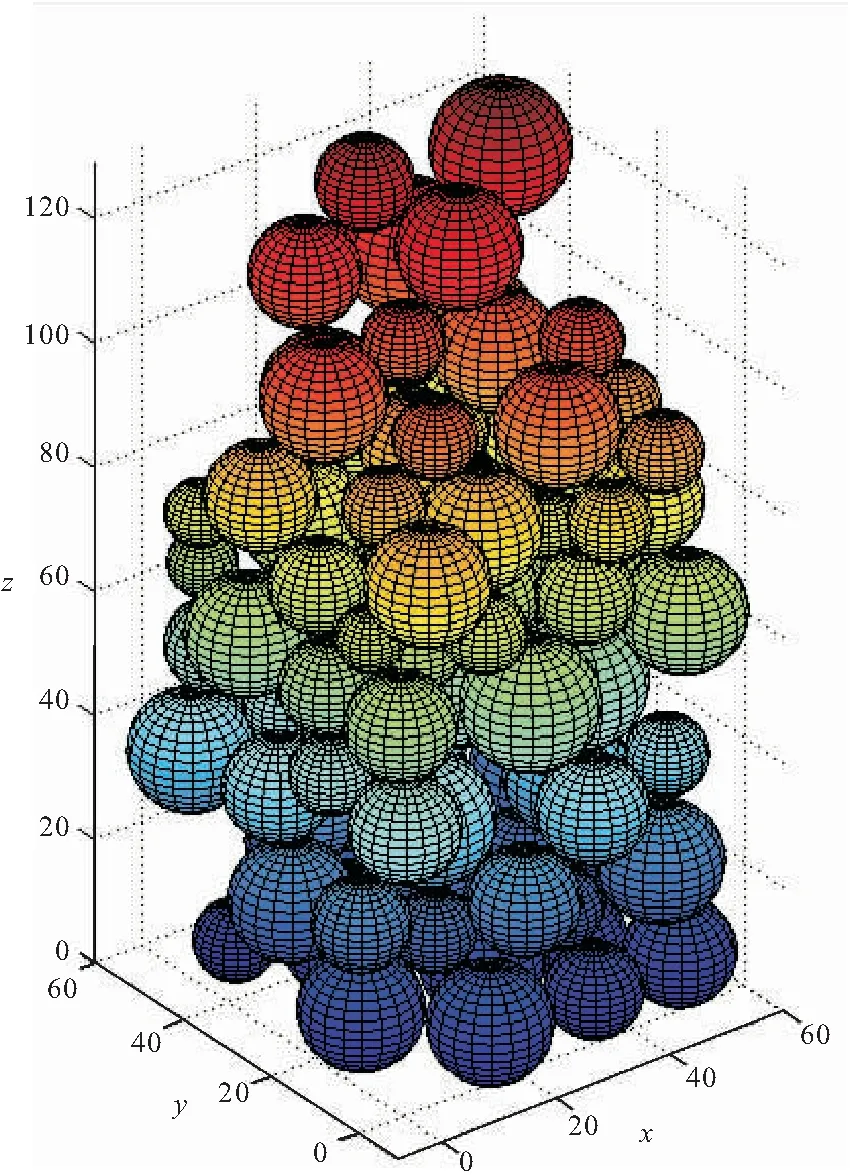
图5 100个颗粒时沉积图

3 岩心特征

由统计函数来描述岩心特征，常用的有：单点概率函数、自相关函数、线性路径函数。

3.1 单点概率函数

在一般实际情况处理中，将二维或三维系统离散化，每个离散点像素值由相函数确定。需对离散点值进行统计即可得到孔隙度值。假设100个颗粒沉积，压实因子取0.4，沉积区域为60×60×60，进行孔隙度计算，统计得到该模型孔隙度为0.375。沿x、y、z不同方向进行切片，获得不同孔隙度，如图6所示。

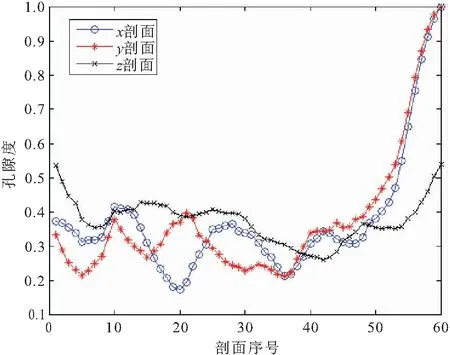
图6 不同方向剖面孔隙度

3.2 自相关函数

通常将岩心模型近似成各向同性，自相关函数值S(r)沿三个方向分别统计平均得到。

当计算长度超过自相关距离后，自相关函数的取值不再变化，因而自相关函数值可取曲线达到稳定值或水平波动不大的对应值。取z=20剖面做自相关函数计算，图7为图6图像中孔隙系统所对应的自相关函数曲线。当像素值r=0时，自相关函数值S(r)为0.388，即z=20剖面的孔隙度值。

图7 自相关函数曲线

3.3 线性路径函数

图8为图7孔隙系统所对应的线性路径函数曲线。由图8可知，x、y方向线性路径函数曲线重合，当两点跨距约达到40个像素点时路径函数L(r)取值趋于稳定，z方向线性路径函数当两点跨距约达到30个像素点时路径函数L(r)取值趋于稳定。说明该系统z方向经过了压实。体空间线性路径函数当两点跨距约达到35个像素点时路径函数L(r)取值趋于稳定，系统内部孔隙相线性连通范围的最大值约为35个像素。

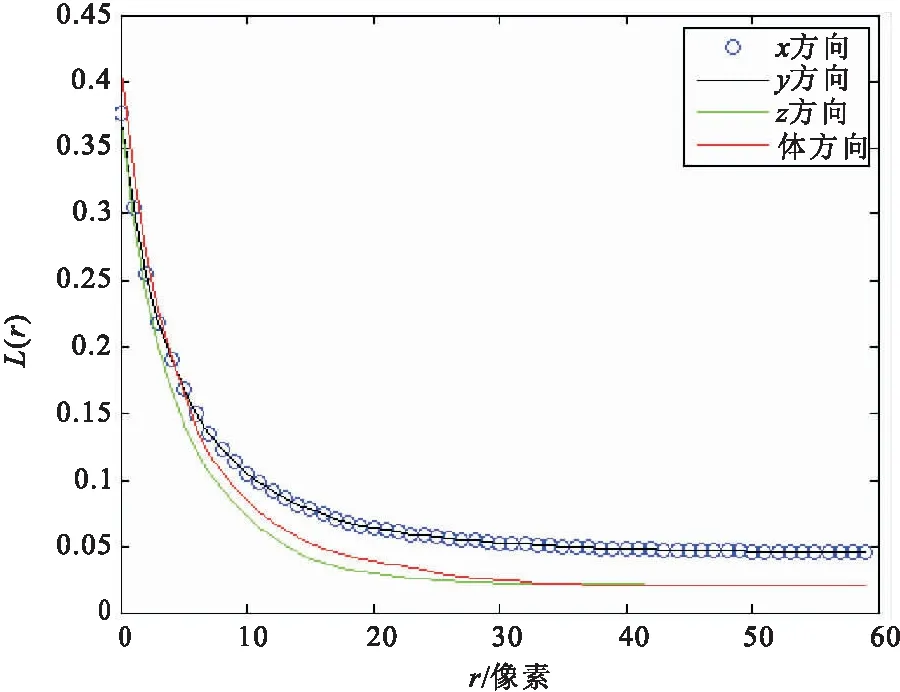
图8 线性路径函数曲线

3 结 论

通过过程模拟法建立的数字岩心具有良好的均质性、连通性和各向同性。采用过程法建立不同粒径的数字岩心，可以观察对岩石物理属性的影响，不同的岩石粒径导致不同的岩石孔隙结构。

在沉积模拟时，沉积颗粒是在粒度组成分布曲线上随机选择的，对于相同的粒度组成分布曲线，每次模拟得到的沉积结果都略有不同。为了简化运算，便于网格离散化，本文的颗粒半径是在一个整数范围内随机得到的。

沉积过程的模拟是整个过程模拟法中最重要、工作量最大的部分，每次颗粒沉积时的膨胀曲面都在变化，确定膨胀曲面方程非常重要。在模拟沉积过程时引入了网格化计算的方法，简化了工作量，加快了运算速度。