基于捷联惯性导航的矿用单轨吊机车定位算法

2021-01-26郭梁宋建成宁振兵王明勇吝伶艳黄健琦

工矿自动化 2021年1期

郭梁，宋建成，宁振兵，王明勇，吝伶艳，黄健琦

(1.太原理工大学电气与动力工程学院，山西太原 030024；2.太原理工大学矿用智能电器技术国家地方联合工程实验室，山西太原 030024；3.太原矿机电气股份有限公司，山西太原 030032)

0 引言

单轨吊机车是煤矿井下用来运送材料、设备和人员的先进辅助运输设备。与传统的辅助运输方式相比，单轨吊机车具有运输效率高、坡度大、不受巷道地面影响等特点。尽管这种运输方式优点突出，但其定位方式落后，目前仍以定位精度较低的射频识别(Radio Frequency Identification，RFID)定位和接收信号强度指示(Received Signal Strength Indication，RSSI)定位为主，难以满足工业应用需求。据2013—2017年我国煤矿事故统计，运输事故数占煤矿事故总数的17.48%，运输事故死亡人数占煤矿事故总死亡人数的10.85%[1]，这与矿井辅助运输机车无法精确定位有直接关系。此外，在不确定机车位置的情况下，无法实现机车的统一调度，会出现多辆单轨吊机车拥堵的情况，运输效率较低。因此，开发单轨吊机车高精度定位系统具有重要的现实意义。

目前，应用于煤矿井下的定位技术有RFID、RSSI、超宽带(Ultra Wide Band，UWB)、捷联惯性导航等定位技术。文献[2]设计了一种基于RFID和ZigBee技术的矿井机车精确定位系统，该系统通过RFID技术实现位置的更新，以ZigBee技术实现数据的传输，电子标签密度越高，定位精度越高，但这会导致成本上升。文献[3]设计了一种基于ZigBee的钨矿井下矿车定位监测系统，该系统利用RSSI测距模型和加权质心定位算法实现了矿车定位，与极大似然估计算法相比，定位精度较高，但该系统需要较多的参考节点，定位成本高。文献[4]提出了一种基于RSSI的矿山井下机车定位算法，利用最小二乘法和chan算法实现机车的定位，最小定位误差为0.4 m，但该方法也需要较多参考节点才能实现精确定位，定位成本高。文献[5]设计了一种基于UWB的矿井机车定位系统，该系统利用UWB技术和到达时间差(Time Difference of Arrival，TDOA)定位算法实现机车定位，定位精度达10 cm，但该系统在实现某一区域的定位时，需要1台同步控制器和多台定位基站，成本较高。文献[6]设计了基于惯性导航的煤矿移动车辆定位系统，该系统采用六轴惯性测量单元(Inertial Measurement Unit，IMU)实现对车辆的定位，然而，六轴IMU解算出的航向角误差较大，难以对机车进行长期、准确的定位。

针对以上定位方法存在的问题，本文提出了一种基于捷联惯性导航的矿用单轨吊机车定位算法，该算法不仅提高了单轨吊机车的定位精度，而且降低了定位成本。

1 定位流程

捷联惯性导航系统(Strapdown Inertial Navigation System，SINS)是一个将IMU固定于载体上的独立定位系统[7]，已广泛应用于需要定位的各种工程领域[8]。基于SINS的矿用单轨吊机车定位流程如图1所示。

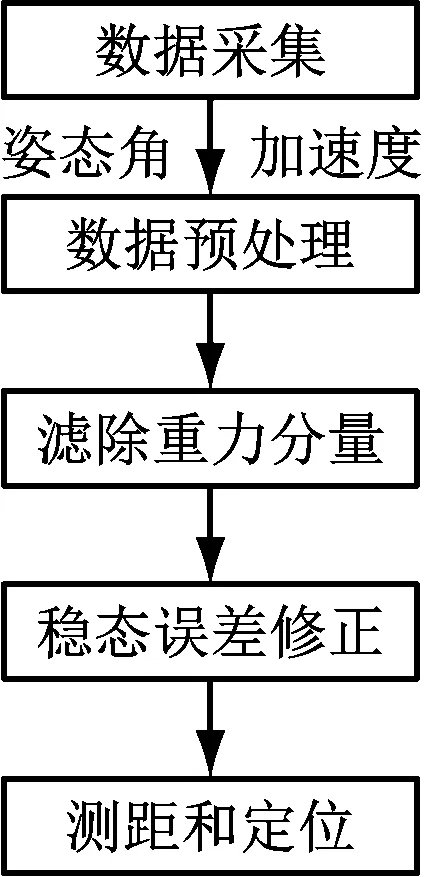
图1 基于SINS的矿用单轨吊机车定位流程

利用九轴IMU(包括三轴加速度传感器、三轴陀螺仪、三轴磁力计)采集机车数据，解算并输出姿态角和加速度值。为了滤除加速度数据中的确定性误差和尖峰噪声，需对其进行预处理。由于加速度数据中含有重力分量，当机车在斜坡上行驶时该分量会对测距造成巨大干扰，因而采用方向余弦矩阵法滤除该分量。在积分测距的过程中，通过加速度变化率阈值法和零速修正法修正稳态误差，根据机车测距结果和初始位置实现定位。

2 数据采集与预处理

2.1 数据采集

采用WT931模块采集数据，该模块集成了高精度的微机电系统(Micro-Electro-Mechanical System，MEMS)加速度计、陀螺仪、磁力计，可分别采集机车的三轴加速度、三轴角速度、三轴磁场强度数据。对加速度积分可以得到机车的行驶距离。以加速度、角速度、磁场强度数据为基础，利用卡尔曼滤波算法可以精准地输出机车的实时姿态角。

2.2 数据预处理

尽管MEMS加速度传感器具有体积小、质量小、功耗低、成本低、易集成等优点[9]，但其采集到的加速度数据中仍存在误差和噪声，所以，必须对加速度数据进行预处理。

MEMS加速度传感器采集到的加速度数据中的误差和噪声主要包括确定性误差、随机误差、尖峰噪声等[10]。误差模型为

a=a0+Kar+R+P

(1)

式中：a为加速度测量值；a0为零偏；K为刻度因数；ar为加速度理论值；R为随机噪声；P为尖峰噪声。

WT931模块中集成了高精度的BMI160六轴传感器，该传感器可输出高精度的三轴加速度和三轴角速度数据，加速度中所含的随机噪声很小，因此，可不考虑其影响。零偏、刻度因数、尖峰噪声均会对加速度测量值造成较大干扰。本文分别采用均值法和限幅滤波法滤除零偏和尖峰噪声，采用翻滚法计算刻度因数。

2.2.1 零偏滤除方法

零偏是指加速度传感器输入为0时的输出量，它是由加速度传感器本身的制作工艺引起的误差。对于零偏，可采用均值法滤除。以Y轴为例，首先将WT931模块置于水平台上(Y轴平行于台面)，连续采集2 000个加速度数据并求出均值aav，此后，用采集到的加速度数据减去aav即可滤除零偏[11]。

2.2.2 尖峰噪声滤除方法

尖峰噪声是由传感器本身的技术问题引起的，它具有幅值大、持续时间短等特点。本文根据限幅滤波的思想来滤除尖峰噪声。已知加速度传感器的量程为±2g(g=9.8 m/s2)，假设相邻2次采样值为an-1和an，如果an的绝对值超过了2g，则令an等于前一时刻的值an-1；如果an的绝对值小于或等于2g，则不对an进行处理[12]。

(2)

式中an为n时刻的加速度。

2.2.3 刻度因数计算方法

刻度因数是指加速度传感器输出量与输入量之比。由于MEMS加速度传感器的折叠梁加工尺寸不一致和微机械结构质心偏离平衡位置等原因[13]，刻度因数为未知的常数。本文根据12位置重力翻滚法的思想，采用翻滚法来求取刻度因数。

以Y轴为例，将WT931模块置于水平台上，将Y轴与水平台的夹角依次调整至90°和-90°，待数据稳定后分别采集2 000个Y轴加速度数据并求取均值aY1和aY2，根据均值可以求出刻度因数，计算公式为

KY=(|aY1|+|aY2|)/2g

(3)

式中KY为Y轴的刻度因数。

3 重力分量滤除方法

惯性模块WT931中的加速度传感器既能检测到静态加速度(重力加速度)，又能检测到动态加速度(运动加速度)[14]。当单轨吊机车在斜坡上运动时，重力加速度(即重力分量)的存在会对运动加速度产生干扰，这会严重影响单轨吊机车的定位精度。因此，本文采用方向余弦矩阵法滤除重力分量。

设方向余弦矩阵为C，C为3阶方阵：

(4)

设机车所在的坐标系为载体坐标系OXbYbZb(b系)，用于定位的坐标系为导航坐标系OXnYnZn(n系)，导航坐标系的方向为东北天，分别对应XYZ轴[15-16]。从导航坐标系到载体坐标系可视为3个有序的旋转过程，每个旋转过程用绕单轴旋转的余弦矩阵来表示[17]。

绕X轴旋转α(俯仰角)得到的余弦矩阵为

(5)

绕Y轴旋转γ(横滚角)得到的余弦矩阵为

(6)

绕Z轴旋转θ(航向角)得到的余弦矩阵为

(7)

假定从导航坐标系到载体坐标系依次绕Z,X,Y轴旋转，相应的姿态矩阵为

(8)

由此可得出重力加速度在载体坐标系各轴上的分量为

(9)

用采集到的加速度值减去重力加速度在载体坐标系各轴上的分量gx,gy,gz，即可滤除重力分量。

4 稳态误差修正算法与测距算法

稳态误差修正算法包括稳态加速度误差修正算法和稳态速度误差修正算法，测距算法包括Lagrange插值多项式测距算法和测距结果定时修正算法，这2部分算法对定位精度起决定性作用。

4.1 稳态误差修正算法

4.1.1 稳态加速度误差修正算法

由于MEMS加速度传感器的精度有限，当其静止或匀速运动时的加速度值总在0附近小幅波动，即存在稳态加速度误差。通过分析数据发现，传感器处于静止与变速运动时的加速度变化率幅值有较大差异，因此，本文提出了加速度变化率阈值法，用以修正此误差。

设a1，a2，…，a10为连续10个加速度值，u为这10个数据的均值，T为采样周期。以10个数据为1组，用组内相邻2个数据求出1个加速度变化率并取绝对值，由此可得：b1=|(a2-a1)|/T，b2=|(a3-a2)|/T，…，b9=|(a10-a9)|/T。用d表示9个数据中大于w(w为经验值，此处取0.1 m/s3)的个数，d最大为9。如果d<8且|u|<0.25 m/s2，则将这10个数据置0；否则，对其不做任何处理[18]。

加速度修正前后曲线比较如图2所示。从图2可看出,在15～20 s，加速度修正前,机车几乎是减速运动，而此时机车实际是近似匀速运动；修正后的加速度始终为0，修正了稳态加速度误差。

图2 加速度修正前后曲线比较

4.1.2 稳态速度误差修正算法

机车的速度由加速度积分得来，因此，机车在行驶过程中的加速度误差会导致其停车时的速度不为0[19]，即存在稳态速度误差。根据停车时的特点，本文提出零速修正法修正稳态速度误差。

设an为n时刻的加速度，vn为n时刻的速度，n=0,1,…，vco为一个速度常数(此处取0.005 m/s)。如果vn≤vco且an，an-1，an-2均小于0，则令vn=0，否则不对vn做处理[20]。

机车运行时要经历静止、变速运动、静止3个阶段。无零速修正与有零速修正时的速度变化曲线分别如图3、图4所示。

图3 无零速修正时的速度变化曲线

图4 有零速修正时的速度变化曲线

由图3和图4可知，无零速修正时，停车时的速度为负值，无法正确反映机车的运动状态；有零速修正时，停车时的速度为0，可正确反映机车的运动状态。

4.2 测距算法

4.2.1 Lagrange插值多项式测距算法

测距算法是实现准确定位的核心，它的优劣将直接导致累计误差的产生，因此，本文基于Lagrange插值多项式测距算法[21]，提出了含有4个插值节点的Lagrange插值多项式测距算法。

设4个插值节点分别为(x0,y0),(x1,y1),(x2,y2),(x3,y3)，对应的插值多项式如下：

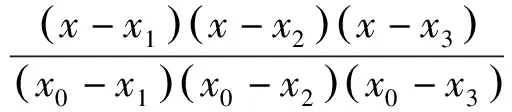
(10)

在计算机车速度时，相应插值节点分别为(0,a0),(T,a1),(2T,a2),(3T,a3)，a0—a3为按时间顺序采集到的4个加速度，a3为当前时刻的加速度。将这4个插值节点代入f(x)中，得到函数A(x)，对A(x)进行积分即可计算出机车速度。

(11)

式中：vno为当前时刻机车速度；vla为上一时刻机车速度。

在计算机车行驶距离时，相应的插值节点分别为(0,v0),(T,v1),(2T,v2),(3T,v3)，v0—v3为按时间顺序求得的4个速度，v3为当前时刻的速度。将这4个插值节点代入f(x)中，得到函数V(x)。对V(x)进行积分即可计算出机车的行驶距离。

(12)

式中：hno为当前时刻的行驶距离；hla为上一时刻的行驶距离。

4.2.2 测距结果定时修正算法

为了提高测距精度，防止测距时出现过大的误差，提出测距结果定时修正法来修正测距误差。因为单轨吊机车的行驶速度通常为1～2 m/s，所以可通过实验数据对其在给定时间内的测距结果进行估计。如果给定时间内的测距结果与其估计值的差的绝对值大于阈值hth(hth为常数，此处取0.8 m)，则可将测距结果修正为估计值,否则保持原测距结果。

(13)

式中：ΔH为给定时间内的测距结果；Δhes为给定时间内的测距结果估计值。