三维集成电路稳态解和瞬态解的建模与热分析*

陈品忠， 潘中良

（华南师范大学物理与电信工程学院， 广州 510006）

1 引言

随着集成电路特征尺寸的减小，作为集成电路重要组成的铜互连的延迟、噪声和功耗却不断增加。 解决互连延迟（特别是全局互连）对性能的影响最终只能通过降低互连长度的途径来实现。 三维集成技术在垂直方向进行堆叠，相邻层之间通过垂直互连实现电学连接，这为集成电路的互连提供了一个可行的技术方案[1]。 三维集成具有更高的器件集成度，芯片面积更小。 然而，三维集成电路的散热仍旧需要通过芯片的上下表面来进行，因为随着芯片面积的减小，散热能力有所下降，这使得热管理问题成为限制三维集成电路发展的主要因素之一[2]。

文献[3]使用顶层均匀分布热源，获得了含有硅通孔等复杂模型的温度场。 文献[4]使用紧凑热模型分析了3D IC 的横向传热。 文献[5]分析了在顶层含有非均匀分布热源情况下的热模型，并且计算出了等效的导热系数。 文献[6]讨论了在模型材料为各项异性情况下的2 层3D IC 的稳态热传导问题的解。 文献[7]使用迭代模型计算了3 层3D IC 温度场的稳态和瞬态分布，虽然文中指出迭代次数少， 但是相比非迭代模型，计算量仍旧偏大。文献[8]解决了迭代问题，得到多层3D IC 模型的稳态解析解， 但是没有计算出瞬态解析解。文献[9]只用1 条解析式同时表示3 层模型稳态和瞬态的非迭代解，瞬态解是直接的，但是稳态解是间接的， 因为稳态解需要在瞬态解时间t 趋于无穷大的情况下得到。

本文分别给出了适用于N 层3D IC 的热源非均匀分布的稳态解和瞬态解，其中N≥2，当确定源的分布和数值之后，解析解就可以直接得出；瞬态时热源值的大小可以随时间变化。

2 三维集成电路热模型的建模

三维集成电路热模型如图1 所示，图1（a）表示N层堆叠的热模型，图1（b）表示第i 层的矩形热源分布。模型的长和宽分别为a、b，总厚度为zN。 在三维集成电路中，热源q 是产生功耗的主要部分，放置在每一层的顶部，矩形形状契合一般芯片形状，而数量可以是任意的。 热源q 厚度不考虑，因为在三维集成电路中，该部分厚度相对来说是非常薄的。 散热片/散热器在模型的最底部，最底部温度假设为25 ℃。在实际应用中，模型侧面、顶面可以假设为热绝缘的，因为它们的散热效果相对底面会差很多。

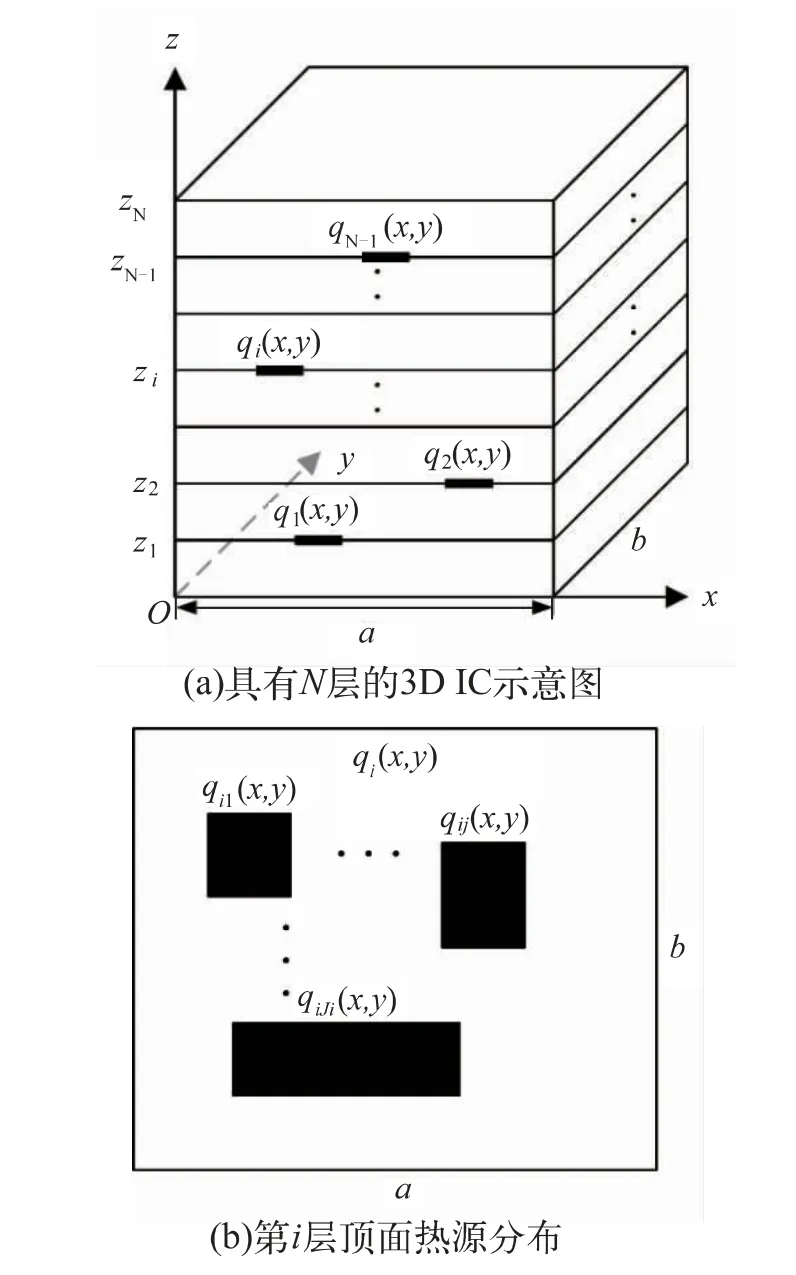
图1 三维集成电路热模型

令U1代表稳态温度场分布函数，那么稳态热分析中该模型的热扩散方程可以为：

q1i表示稳态问题中第i 层热源；Δ 是拉普拉斯算符；系数k 代表热导率，尽管多数材料的热导率k 都是温度的函数，由于芯片工作温度范围较小，为了简单，在这里将每层k 视为同一常数， 并且是均匀各项同性的。 令U2代表瞬态温度场分布函数，瞬态热分析中该模型的热扩散方程可以为：

ρ 代表材料密度，C 为比定压热容， 将每层ρ 和C也分别统一为相同的常数。 q2i表示瞬态问题中第i 层热源，t 为时间。 在稳态和瞬态热传导问题中，都假设侧面(x=0,a 以及y=0,b)和最顶面(z=zN)为热绝缘的，那么函数U1、U2对应的第二类边界条件全是齐次的，底面对应的第一类边界条件非齐次，因此：

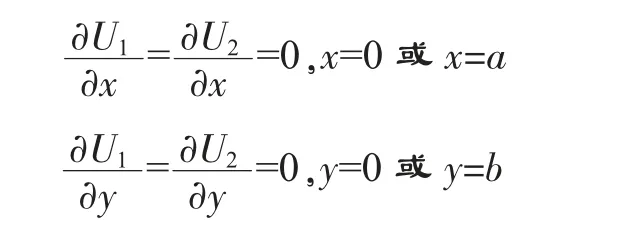
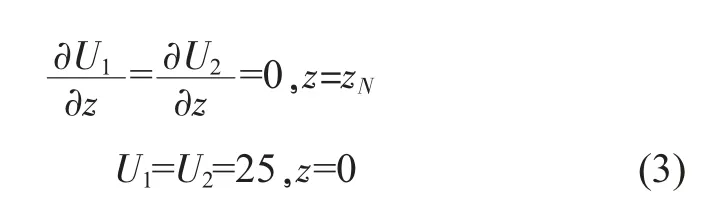
层间温度值连续，热流密度值相差qi，由于瞬态热扩散方程还有U2对t 求偏导部分，需要添加初始条件才能定解：U2(x,y,z,0)=25。

3 解析解

察边界条件可以发现式(3)是非齐次的，考虑将边界条件齐次化。 对于稳态问题，构造辅助函数W1(x,y,z)=25，令U1(x,y,z)=T1(x,y,z)+W1(x,y,z)，根据叠加原理可以得到：

函数T1(x,y,z)和U1(x,y,z)有类似的齐次边界条件，即在x=0,a 或y=0,b 或z=zN时第二类边界条件是齐次的。在辅助函数的影响下，函数T1(x,y,z)的第一类边界条件也是齐次的，即T1(x,y,0)=0。 因此，偏微分方程式(4)的定解条件全是齐次的。

对于瞬态问题，构造辅助函数W2(x,y,z,t)=25，令U2(x,y,z,t)=T2(x,y,z,t)+W2(x,y,z,t)，根据叠加原理可以得到：

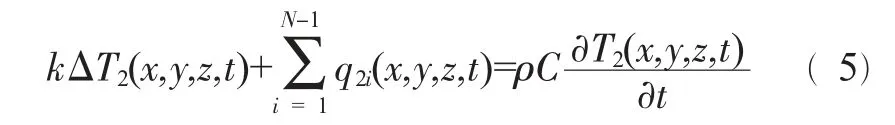
和稳态问题类似，偏微分方程式(5)的定解条件也全是齐次的，不仅包括边界条件T2(x,y,0,t)=0，还包括初始条件T2(x,y,z,0)=0。

因为辅助函数W1、W2是已知的， 所以对函数U1、U2的求解也就转变为对函数T1、T2的求解。 以下主要讨论关于函数T1、T2的求解过程。

3.1 稳态解析解

文献[9]对复杂源的温度场提供了格林函数的思想，可以将格林函数方法运用到这里的求解中。 格林函数一般讨论点源对场的影响，但上述模型热源分布相对简单，为了方便计算，令函数G1i(x,y,z；zi)表示在稳态问题中z=zi时该层顶面热源对模型温度场产生的影响，根据式(4)可以得到一个含有单位冲激函数δ 的等式：ΔG1i=-qi(x,y)/kδ(z-zi)。 那么函数T1和函数G1i的关系则为：

下面来求解函数G1i(x,y,z；zi)，根据分离变量法、本征函数展开法和本征函数正交性得到：

其中n、m 为任意非负整数，α= [(nπ)/a]2，β=[(mπ)/b]2，积分微元dσ 的积分区域是第i 层顶面区域(如图1（b） 所示)，δn0、δm0是kronecker 函数，

根据式(6)、(7)，可获得函数T1(x,y,z)的解。

3.2 瞬态解析解

根据格林函数思想，令函数G2i(x,y,z,t；zi)表示在瞬态问题中z=zi时该层顶面热源对模型温度场产生的影响，根据式(5)可以得到以下等式：ΔG2i+q2i(x,y,t)/kδ(z-zi)=1/μ∂G2i/∂t。 那么函数T2和函数G2i的关系则为：

其中μ=k/(ρC)。 假设热源和时间的关系为q2i(x,y,t)=从1 到Ji，Ji表示 第i 层 热源数 量，p2ij(x,y)表示第i 层第j 个热源，功率大小为1 W/mm2，qij(t)表示第i 层第j 个热源的值随时间变化函数，当qij(t)为常量时表示热源功率不随时间变化。 使用分离变量法、本征函数展开法和本征函数正交性可以得到：

其中n、m、p 为任意非负整数，α= [(nπ)/a]2，β=[(mπ)/b]2，γ=[(p+1/2)π/zN]2，λ=α+β+γ，h(t)是与时间t 有关的单位阶跃函数积分微元dv 的积分区域是整个模型，如图1(a)所示，δn0、δm0是kronecker函数。

根据式(8)、(9)就能够求出T2(x,y,z,t)的解。

4 实验结果与分析

为了验证解的准确性，在这部分将给出稳态解和瞬态解在MATLAB 中计算得到的结果， 并与COMSOL 得到的结果进行比较。首先说明实验统一使用的参数： 模型长a 和宽b 都设为10 mm；z1、z2、z3、z4、z5、z6分别为3 mm、4 mm、5 mm、7 mm、8 mm、9 mm，3层堆叠时模型最高为7 mm (z4)，5 层堆叠时模型最高为9 mm (z6)；k 为1 W/(mm·K)，ρ 为1 kg/mm3，C 为1 J/(kg·K)；使用大中小3 种尺寸的热源，大热源1 mm×8 mm，2 W/mm2，中热源1 mm×2 mm，10 W/mm2，小热源1 mm×1 mm，20 W/mm2。

4.1 稳态热传导问题

稳态问题第1～5 层热源位置分布如图2 所示。 第1 层小热源几何中心分别在(2 mm,6 mm)、(7 mm，5.5 mm)，中热源几何中心分别在(3 mm,2 mm)、(5 mm,4 mm)，大热源几何中心在(5 mm,8.5 mm)；第2 层小热源几何中心在(7 mm,7 mm)，中热源几何中心在(3 mm,5.5 mm)，大热源几何中心在(5 mm,2.5 mm)；第3 层小热源几何中心分别在(5 mm,8 mm)、(3 mm,5.5 mm)，中热源几何中心在(6 mm,4 mm)；第4 层大热源几何中心在(7.5 mm,4.5 mm)；第5 层小热源几何中心分别在(5 mm,5 mm)、(8.5 mm,1.5 mm)。 3 层堆叠时只提供第1、2、3 层热源，顶层(z=7 mm)不布置热源；5 层堆叠时包含1～5 层全部热源。

图2 稳态问题第1～5 层热源位置分布

由于解析解是无穷级数，MATLAB 在工作时需要确定n、m 的值。 为了使结果误差在一定范围内而n、m的值又不会太大，需要进行调试。在使用上述3 层堆叠并且n、m 值相同的情况下，级数上界采用5、11、15、21共4 组数据进行比较： 在稳态解情况下，COMSOL 得到的峰值温度约为39.030 ℃，MATLAB 得到的峰值温度分别为36.186 ℃、38.786 ℃、39.395 ℃、39.640 ℃，所以误差分别为7.29%、0.63%、0.94%、1.56%。 提取模型中峰值温度所在的x-y 平面如图3 所示，图3(a)是n=m=15 时的MATLAB 温度分布图， 图3 (b)是COMSOL 温度分布图，在图中过峰值温度所在点做平行于x 轴的虚线。 图4 除“ COMSOL”以外的4 条温度曲线对应图3(a)虚线上使用不同求和上界求得的温度值，图4“ COMSOL”温度曲线对应图3(b)虚线上的温度值。 “ n=m=15”和“ n=m=11”峰值温度误差都低于1%， 而“ n=m=15” 与“ n=m=21” 这2 条温度曲线和“ COMSOL”温度曲线吻合度都非常高，综合以上2 点因素，稳态解选用求和上界n=m=15。

图3 稳态问题3 层3DIC 峰值温度所在的x-y 平面温度分布

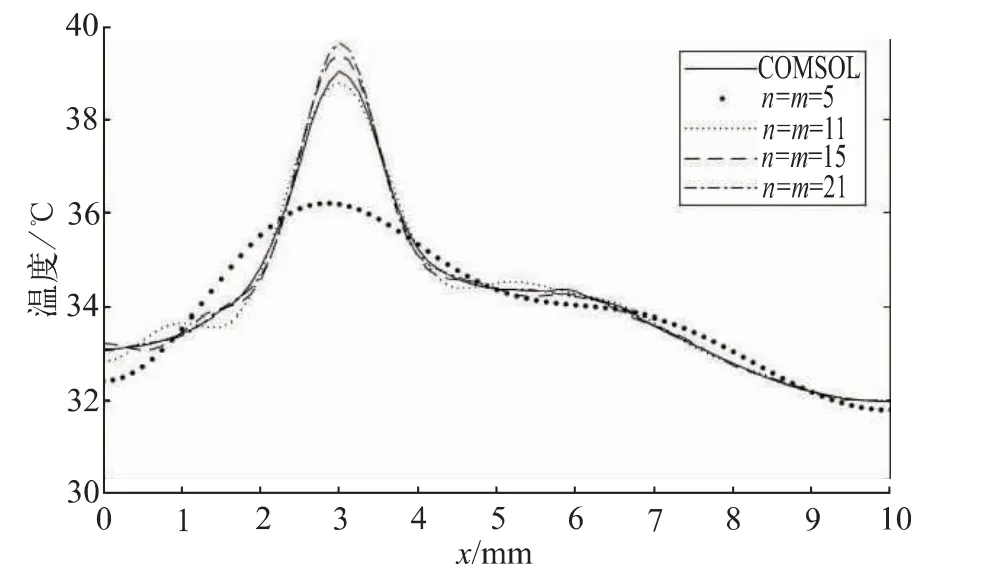
图4 y=5.5 mm,z=5 mm, 沿x 方向3 层3D IC 不同求和上界的温度曲线

稳态问题沿x 方向的温度曲线如图5 所示。 在3层3D IC 模型中令z=4 mm，y=5 mm，沿x 方向提取温度值，得到“ 3 层z=4 mm”温度曲线；在5 层3D IC 模型中令z=7 mm，y=5 mm，沿x 方向提取温度值，得到“ 5 层z=7 mm”温度曲线；在5 层3D IC 模型中找到峰值温度所在x-y 平面，即z=8 mm 时的x-y 平面，根据峰值温度所在的几何点固定y 值(通过仿真确定y=1.5 mm)，沿x 方向提取温度值，得到“ 5 层z=8 mm”温度曲线，“ 5 层峰值温度” 指的是5 层堆叠情况下模型最大温度值。 可以发现，“ 3 层z=4 mm”、“ 5 层z=7 mm” MATLAB 温度曲线和COMSOL 温度曲线基本是重合的， 通过MATLAB 计算得到这2 组曲线最大误差分别为0.30%、0.08%。“ 5 层峰值温度”椭圆标记处温差比较大， 在MATLAB 计算得到该处误差为1.07%。

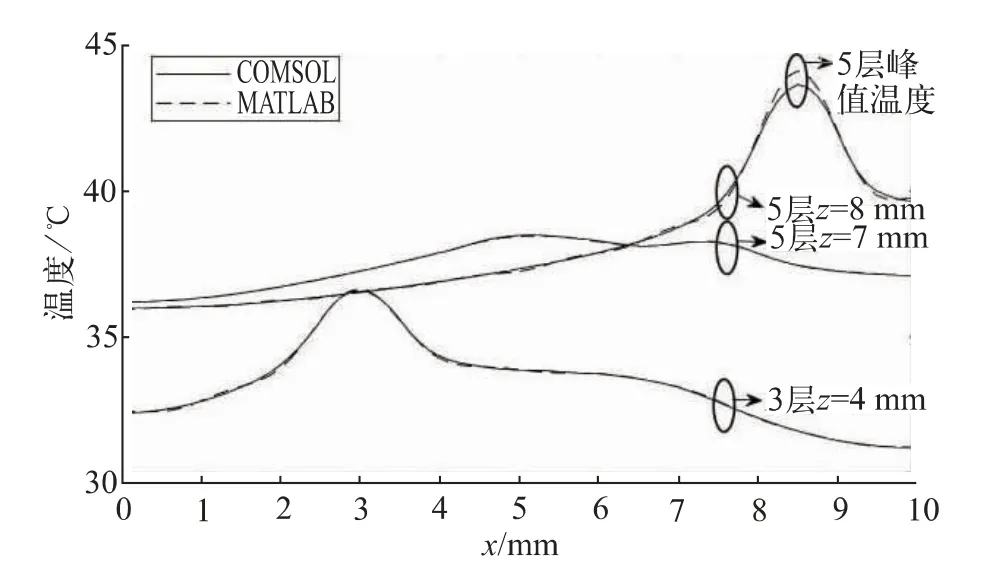
图5 稳态问题沿x 方向的温度曲线

稳态问题沿z 方向温度曲线如图6 所示。 在3 层3D IC 模型中令x=5 mm、y=5 mm， 沿z 方向提取温度值，得到“ 3 层x=5 mm”温度曲线；在5 层3D IC 模型中令x=5 mm、y=5 mm，沿z 方向提取温度值，得到“ 5层x=5 mm”温度曲线。3 层堆叠模型高度只有7 mm，5层堆叠模型高度为9 mm，所以“ 3 层x=5 mm”温度曲线在7≤z≤9 区间没有温度值。 观察图6 可以发现，MATLAB 曲线和COMSOL 曲线吻合度非常高，在MATLAB 中计算“ 3 层x=5 mm”和“ 5 层x=5 mm”曲线最大误差分别为0.33%、1.03%。 对比“ 3 层x=5 mm”曲线和“ 5 层x=5 mm”曲线可以发现，在3 层3D IC 模型基础上再增加2 层热源， 这会导致第1、2、3 层温度整体性提高。 图6 中z=8 mm 时COMSOL 和MATLAB曲线都出现了尖点，即一阶不可导点，这是热源在z 方向上没有厚度导致的。

图6 稳态问题沿z 方向温度曲线

4.2 瞬态热传导问题

瞬态问题第1～5 层热源位置分布如图7 所示。 在瞬态解中各层模型尺寸和3 种热源尺寸都和稳态解的一样，只是热源个数和分布不一样。第1 层小热源的几何中心分别为(4 mm,7.5 mm)、(5 mm,5 mm)、(3 mm，3 mm)，中热源的几何中心为(6 mm,3 mm)，大热源的几何中心为(8 mm,5 mm)；第2 层中热源几何中心分别为(6.5 mm,7.5 mm)、(3 mm,5 mm)；第3 层中热源几何中心为(5 mm,6.5 mm)，大热源几何中心为(8 mm，5 mm)；第4 层小热源几何中心为(5 mm,1.5 mm)，中热源几何中心为(3 mm,8 mm)，大热源几何中心为(5 mm,5 mm)；第5 层小热源几何中心分别为(6.5 mm,8 mm)、(3.5 mm,3.5 mm)，中热源几何中心为(3.5 mm,6.5 mm)。5 层3D IC 包括上述所有热源，3 层3D IC 没有第4、5层热源。

图7 瞬态问题第1～5 层热源位置分布

MATLAB 使用“ n=m=5，p=11”、“ n=m=11，p=21”、“ n=m=15，p=31”、“ n=m=21，p=41”4 组求和上界计算得到在t=1000 s 时3 层3D IC 模型峰值温度分别为32.245 ℃、34.357 ℃、35.182 ℃、35.501 ℃，COMSOL仿真峰值温度为35.423 ℃， 对应误差分别为8.97%、3.01%、0.68%、0.22%。3 层3D IC 模型峰值温度所在的x-y 平面(z=3 mm)如图8 所示。 在这些平面上令y=5 mm，作平行于x 轴的虚线，提取虚线上的温度值得到MATLAB 中不同求和上界的温度曲线和COMSOL 中的温度曲线，结果如图9 所示。可以发现，当求和上界值越大，MATLAB 温度曲线和COMSOL温度曲线的吻合度越高，并且“ n=m=21，p=41”曲线峰值温度误差最小，所以瞬态解选用n=m=21，p=41。

图8 t=1000 s，3 层3D IC 峰值温度所在的x-y 平面温度分布

图9 t=1000 s,y=5 mm,z=3 mm, 沿x 方向使用不同求和上界的3 层3D IC 温度曲线

t=100 s 时沿x 方向的温度曲线如图10 所示。“ 3层z=4 mm” 曲线是3 层3D IC 模型z=4 mm、y=5 mm时沿x 方向的温度曲线，最大误差为0.76%；“ 5 层z=7 mm”曲线是5 层3D IC 模型z=7 mm、y=5 mm 时沿x方向的温度曲线，最大误差为2.22%。t=100 s 时沿z 方向的温度曲线如图11 所示。“ 3 层x=5 mm” 曲线是3层3D IC 模型x=5 mm、y=5 mm 时沿z 方向的温度曲线，最大误差为1.68%；“ 5 层x=5 mm”曲线是5 层3D IC 模型x=5 mm、y=5 mm 时沿z 方向的温度曲线，最大误差为2.49%。 因为3 层3D IC 在z 方向上最大只有7 mm，所以“ 3 层x=5 mm”温度曲线在7＜z≤9 时没有温度值。 由于热源设置为没有厚度，COMSOL 曲线z=3 mm 时出现尖点，但是从式(9)可知，瞬态解无法产生和z 有关的尖点，因为可导，瞬态解在MATLAB 中只能通过不断增加求和上界的方式来无限逼近尖点形状。 图11 和图6 相比，可以发现稳态解却能够在MATLAB 中成功产生尖点，根据式(7)可知，稳态解是以分段函数的方式来产生尖点的。

图10 t=100 s 时沿x 方向的温度曲线

以上讨论的热源都是与时间无关的，现在使用瞬态问题中的5 层3D IC 模型， 全部热源幅值比例设为a， 并且只将第1 层热源的值改为与时间有关的，将2 W/mm2的热源改为a [2+sin (bt))] W/mm2，将10 W/mm2的热源改为a[10+ sin(bt)] W/mm2，将20 W/mm2的热源改为a[20+sin(bt)]W/mm2。在这样的设置前提下得到的实验结果如图12 所示。 MATLAB和COMSOL 在几何中心点 (x=5 mm，y=5 mm, z=4.5 mm)的温度变化曲线是十分相似的：当a=1、b=0.01时， 计算结果和仿真结果之间最大误差为2.30%；当a=1.5、b=0.015 时，最大误差为2.60%；当a=2、b=0.02时，最大误差为2.50%。

图11 t=100 s 时沿z 方向的温度曲线

图12 x=5 mm, y=5 mm,z=4.5 mm 几何点温度随时间变化曲线

5 结论

本文基于一个多层3D IC 模型，给定适当的边界条件，通过分离变量法来解决模型的热传导问题，并且分别给出稳态解析解和瞬态解析解。 该模型可以任意设置热源的尺寸、摆放位置，功率大小可以随时间变化。用3 层和5 层3D IC 模型验证解析解的正确性，解析解的温度场用MATLAB 表示出来， 并且与COMSOL 仿真得到的温度场进行比较。 结果表明，稳态解析解计算3 层3D IC 模型得到的温度结果和COMSOL 仿真结果之间的误差小于1%，计算5 层3D IC 模型误差在1%左右； 瞬态解析解计算3 层3D IC模型得到的温度结果和COMSOL 仿真结果误差小于2%，计算5 层3D IC 模型误差小于3%。这些研究结果可以应用于三维集成电路在预测温度分布方面的设计过程中。