融合图卷积神经网络和注意力机制的PM2.5小时浓度多步预测

傅颖颖 ，张丰 *，杜震洪 ，刘仁义

（1.浙江大学浙江省资源与环境信息系统重点实验室，浙江杭州310028；2.浙江大学地理信息科学研究所，浙江 杭州 310027）

2013年，我国遭遇有观测记录以来最严重的雾霾天气［1］，污染最严重的京津冀地区日均PM2.5浓度高达500 μg·m-3，严重影响了人们的生产生活和身体健康。研究表明，当 PM2.5浓度超过 115 μg·m-3时，身体将感到严重不适［2］。因此，利用历史数据高效准确地预测未来的PM2.5浓度，具有重大的现实意义。

目前，根据PM2.5浓度预测模型类别可将其分为化学机理模型、时空分析模型和深度学习神经网络模型3种。ZHANG等［3］采取“气象化学+传输机制”组合对PM2.5浓度进行在线实时预测；徐文等［4］运用时空自回归移动平均模型预测我国华北地区的日均PM2.5浓度；范竣翔等［5］使用循环神经网络模型，基于过去48 h的空气质量和气象数据预测未来1 h的 PM2.5浓度；黄婕等［6］将我国大陆地区的空气质量监测站点数据处理成时序数据，将Stacking集成策略与卷积神经网络和循环神经网络相融合，预测未来1 h的PM2.5浓度。

然而，上述研究都局限于PM2.5浓度的单步预测，即利用历史PM2.5浓度序列预测未来某时段的PM2.5浓度，尚未有研究开展对PM2.5浓度的多步预测。目前对多步预测的研究主要集中在自然语言处理领域和工业领域，例如，在自然语言处理领域，“编码器-解码器”的序列-序列（Seq2Seq）预测模型已广泛应用于机器翻译，为提高机器翻译的精度，文献［7］提出了注意力机制模型；在工业领域，CHEN等［8］考虑规则风电网中风速的时空相关性，结合卷积神经网络和双向门控循环单元，实现了风速的多步预测；GUO等［9］将全注意力机制应用于时间序列，预测未来分钟级时间窗内秒级的网络流量。但上述研究均未涉及非欧式空间数据及其特征提取。

根据已有研究，针对PM2.5小时浓度多步预测问题，本文以自然语言处理领域中的Seq2Seq预测模型为基础，集合图卷积神经网络提取非欧式空间数据特征的能力以及注意力机制自适应关注特征的能力，提出了融合图卷积神经网络和注意力机制的PM2.5小时浓度多步预测模型，旨在一次性准确预测未来连续多个时间步的PM2.5浓度。通过实验，验证和分析了模型的有效性和优越性。

1 PM2.5小时浓度多步预测方法

1.1 问题描述

PM2.5小时浓度多步预测问题本质上是利用一个时间序列预测另一个时间序列的问题，即利用历史M个连续时间步的PM2.5浓度数据，预测未来N个连续时间步的PM2.5浓度，通过观测窗口xobs=[xt-M+1，…，xt]对预测窗口xpre=[xt+1，…，xt+N]进行预测，PM2.5小时浓度多步预测示意如图1所示。

图1 PM2.5小时浓度多步预测Fig.1 Multi-step prediction of PM2.5hourly concentrations

每个空气质量监测站点都有各自的时间序列，可将某一时刻所有空气质量监测站点的PM2.5浓度数据的空间分布抽象成一张无向拓扑图。先提取该站点每个时间步上的空间特征，形成空间特征时间序列，再对基于空间特征时序依赖关系的时间序列解码，得到目标PM2.5浓度序列。

1.2 PM2.5小时浓度时空相关性分析

通过单位根检验（ADF）和全局空间自相关分析，简要说明PM2.5小时浓度的时空关联性。

用ADF对北京市2015—2016年的PM2.5小时浓度序列进行平稳性检验，实验结果如表1所示。假设序列存在单位根，ADF得到的统计检验值为-13.0573，小于99%，95%，90%3种置信区间的临界值，且p值接近于0，因此拒绝原假设。也就是说，从研究时间范围看，PM2.5小时浓度序列是平稳的，PM2.5小时浓度数据的历史和现状具有代表性和可延续性。

表1 PM2.5小时浓度序列单位根检验结果Table 1 ADF results of PM2.5hourly concentrations

将北京市2015—2016年22个空气质量监测站点的PM2.5小时浓度数据按照春季（3—5月）、夏季（6—8月）、秋季（9—11月）、冬季（12—次年2月）划分，分别汇总得到各监测站点在不同季节的PM2.5小时浓度均值，使用GeoDA软件进行全局空间自相关分析，分析结果以Moran’s I散点图的形式展示，见图2。春、夏、秋、冬4个季节PM2.5小时浓度全局空间自相关 Moran’s I分别为 0.510，0.611，0.601，0.469，各季节北京市PM2.5小时浓度均呈较高的空间自相关性，空间集聚特征显著，其中春、冬两季的空间自相关性较弱，夏、秋两季的空间自相关性较强。

1.3 图卷积神经网络

由地理学第一定律［10］及1.2节的空间分析可知，PM2.5小时浓度在空间上具有相关性。卷积神经网络（convolutional neural network，CNN）是包含卷积计算且具有深度结构的前馈神经网络［11］，其实质是在规则矩阵上平移共享参数的过滤器，同时计算中心像素点与相邻像素点的加权和，从而实现空间特征的提取，其核心是平移不变性。然而，在进行空间特征提取时，由于PM2.5小时浓度来自空气质量监测站点的记录数据，每个监测站点邻近的站点数不一定相同，无法保证平移不变性，因此，无法直接使用CNN提取空间特征。考虑某一时刻所有监测站点的PM2.5小时浓度数据的空间分布可以被抽象成一张无向拓扑图，因此，本文选择图卷积神经网络，以有效提取拓扑图数据结构的空间特征。

将某时刻S个空气质量监测站点的PM2.5小时浓度数据的空间分布抽象为一张空间图，记为G=（V，E，A），其中，V∈RS×P为点集，P为每个站点的属性维度；E∈RS×S为边集，表示各站点之间的连通性；A∈RS×S为G的空间邻接矩阵，元素Aij表征图节点vi和vj之间的相对空间关系。基于站点之间的空间距离构建邻接矩阵A。若站点vi的地理坐标为（loni，lati），i∈［0，S），则站点vi和站点vj的空间距离为G中每个站点都会产生采样频率一致的污染物浓度序列数据，由此组成图序列数据，见图3。

图卷积操作发生在空间维度，首先只考虑一个时间片上的空间图G。图卷积神经网络层接受某时间片上的G，通过某种卷积操作提取空间特征，然后，将G中每个节点的原始特征转化为具有各自空间特征的隐层。由于图数据无法保持平移不变，因此，与卷积神经网络类似，用过滤器在空域上进行特征提取显得极为不便。图卷积神经网络提取特征最常用的是图谱理论方法［12］，傅里叶变换可从空域变换至频域求解，通过拉普拉斯矩阵将网格数据中的卷积操作推广至图结构数据［13］。

由于对图信号进行卷积后再做傅里叶变换等于对图信号进行傅里叶变换后的乘积［14］，所以图的卷积等价为

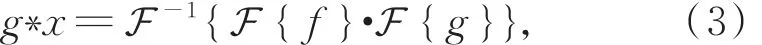
其中，g为图过滤器，x为图信号，*表示卷积，F和F-1分别为傅里叶变换与逆变换。傅里叶变换与逆变换的关键是求得基e-2πit·v和基e2πiv·t（其中，v为频域中的变量，t为空域中的变量，i为虚数单位）。拉普拉斯算子是实对称矩阵，具有良好的性质，如易进行特征分解，且其特征向量是傅里叶变换基［15］。在图G中，拉普拉斯算子L可用图的度数矩阵D∈RS×S和邻接矩阵A∈RS×S表示：

其中，di为节点vi的度。拉普拉斯算子L的特征分解式为

其中，UT对应傅里叶变换基 e-2πit·v，U对应傅里叶逆变换基 e2πiv·t，Λ为特征值组成的对角矩阵，记作

又由式（3），图G的卷积等价为

由式（6），可将UTg看作参数为L的函数g（L），进一步将其看作参数为θ的函数gθ(Λ)。为降低计算复杂度，对gθ(Λ)做切比雪夫多项式的K阶截断近似［12］：

其中，取K=1，λmax=2，此时可得图卷积的一阶线性近似：

令 θ= θ"0=-θ"1，记图 卷积为

将θ看作权值，加上激活层，可得最终的图卷积神经网络的前向传播式为

由于采用的是切比雪夫多项式的一阶近似，图卷积只能建立一阶邻居依赖，若建立K阶邻居依赖，需堆叠多个图卷积层。本文采用两层图卷积神经网络，前向传播式为

其中，H0为节点集V，H2为图卷积神经网络的最终输出特征。神经网络通过反向传播修改参数矩阵W1和W2，以获得邻接节点的最优特征组合，即提取站点间的空间关系。

1.4 Seq2Seq预测模型

由于循环神经网络（recurrent neural network，RNN）可以很好地关联上下文信息，故常被用于序列数据建模［16］。Seq2Seq模型，又称编码器-解码器模型，是RNN的一个重要变种。编码器将输入向量编码成一个长度固定的上下文向量，解码器将上下文向量解码为目标序列。Seq2Seq模型最常见的结构是用2个RNN结构充当编码器和解码器，编码器RNN的最后一个隐状态作为上下文变量［17］。

本文选择门控循环单元（gated recurrent unit，GRU）作为编码器和解码器。普通RNN在时间序列较长的情况下易出现梯度消失或梯度爆炸等问题［18］，长 短 期 记 忆（long short-term memory，LSTM）神经网络通过引入的3个门函数控制信息传递，以克服长距离记忆消失的问题［19］，GRU为LSTM网络中一种效果较好的变体，其结构较简单、且容易训练。

图卷积神经网络提取的空间特征组成时间序列矩阵，作为编码器的整体输入，编码器每次接受一个时间步的输入向量，经GRU门函数，输出该时间步的输出向量和状态向量，然后将状态向量与下一个时间步的输入向量同时输入编码器，循环至输入序列的最后时间步。编码器最终输出的为压缩了输入序列整体信息的状态向量和输出序列矩阵。输出的状态向量将作为解码器的初始状态向量，而解码器的输入向量在训练阶段和预测阶段有所不同。在训练阶段，采用 Teacher Forcing 策略［20］，取上一个时间步的真实数据作为当前时间步的输入向量，神经网络将参数快速更新至合适的值；在预测阶段，则将上一个时间步的输出向量作为当前时间步的输入向量，因此不可避免地会产生误差累积，造成预测精度衰减。编码器-解码器模型的工作示意如图4所示。

图4 编码器-解码器模型的工作示意Fig.4 Schematic diagram of encoder-decoder model

1.5 注意力机制

编码器-解码器模型的缺陷是上下文向量的表征能力有限，无法包含输入序列的所有信息，从而限制，解码器的解码能力。研究发现，注意力机制可以有效缓解序列预测模型中的信息衰减［7］。由于编码器将更多信息分散地保存在每个时间步的输出向量中，注意力机制允许解码器不只依靠上下文向量完成解码，而是在每个时间步上考虑编码器的所有输出向量，通过分配权重，加权求和得到解码器在当前时间步最关注的信息。

其中，WQ为dx×dq维的Query参数矩阵，WK为dx×dk维的Key参数矩阵，WV为dx× dv维的Value参数矩阵，dq=dk。WQ、WK、WV的作用与全连接神经网络中的权重矩阵类似，需要通过反向传播算法更新参数。目标值与Query参数矩阵相乘使得目标值从dx维度的xtk向量映射为dq维度的Q向量，同理，xts-te矩阵映射为元素维度为dk的K矩阵和元素维度为dv的V矩阵。K与V都是对依赖序列的另一种表达，区别是K用于衡量目标值与依赖序列的相关性，即求解权值，V用于计算权值与依赖序列的加权和，即求解注意力机制的输出。xtk向量可来自依赖序列xts-te，也可来自其他序列，若来自依赖序列xts-te，则称该注意力机制为自注意力。

目标值与依赖序列之间的关系为

其中，softmax为深度学习中的softmax激活函数，将数据归一化（0，1）区间：

将权值矩阵与依赖序列加权求和，可得注意力向量

为提高目标值与依赖序列之间注意力的表达能力，增强注意力的广度和深度，文献［7］进一步提出了多头注意力机制（multi-head attention）概念，即使用H组（WQ、WK、WV）参数矩阵，计算同一组目标值和依赖序列的H次注意力机制，得到H个注意力向量，将H个注意力向量拼接成一个向量，作为注意力机制的最终输出结果。

1.6 融合图卷积神经网络和注意力机制的PM2.5小时浓度多步预测模型

本文提出的PM2.5小时浓度多步预测模型可简写为GCN_Attention_Seq2Seq，由图卷积神经网络、GRU编码器和GRU解码器3部分堆叠而成，其中，GRU编码器和GRU解码器与多头注意力机制连接，GRU解码器内部使用多头自注意力机制以提取待解码时间步的输入与已解码的所有输出间的关系。

图5 GCN_Attention_Seq2Seq模型结构Fig.5 Model structure of GCN_Attention_Seq2Seq

图5 为处于预测模式的GCN_Attention_Seq2Seq模型结构，处于训练模式时，解码器每个时间步的输入都由实测值代替。图5说明如下：

①编码器最后一个时间步的输出经过全连接层得到预测值，该预测值经图卷积操作后作为解码器第一个时间步的输入。

②将编码器最后一个时间步的状态向量作为解码器的初始状态向量。

③解码器在解码当前时间步时，将该步的输入向量作为目标值、已解码得到的所有输出向量作为依赖序列，计算得到自注意力向量。自注意力向量用于衡量解码器内当前时间步的输入对解码器当前所有输出的依赖程度。自注意力向量与上一步输出的状态向量相加作为新状态向量。

④解码器在解码当前时间步时，将第③步得到的新状态向量作为目标值，将编码器的输出矩阵作为依赖序列，计算得到注意力向量。

⑤将第④步得到的注意力向量作为输入当前时间步的最终状态向量，用于解码。

本文将最原始的编码器-解码器（Seq2Seq）模型和使用图卷积神经网络、未使用注意力机制的编码器-解码器（GCN_Seq2Seq）模型作为对照模型，以说明图卷积神经网络和注意力机制的作用。3个模型在编码器部分无区别，而在解码器部分，GCN_Attention_Seq2Seq模型较其他2个模型增加了多头注意力机制和多头自注意力机制。

2 实例验证与结果分析

2.1 实例与实验配置

实验样本为2015年1月1日至2016年12月29日北京市36个空气质量监测站点的空气污染物小时浓度数据，污染物包括 PM2.5、PM10、NO2、CO、O3和SO2共6种，数据来源于中国环境监测总站的全国城市空气质量实时发布平台。由于监测站点采集到的原始数据有不同程度的缺失，故去除数据缺失率大于2%的污染物和监测站点，最终保留了22个空气质量监测站点和 PM2.5、SO2、NO2、O3共 4 种污染物，共形成382 998条原始空气质量记录数据。空气质量监测站点分布及其拓扑图如图6所示。

首先，对原始记录数据进行预处理。然后，对382 998条记录以时间为行索引、站点ID为列索引进行排列，规整为17 410行。每一行的各站点间用“#”号间隔，每个站点中的污染物浓度属性用“，”间隔。缺失值用线性插值的方式补全。最后，将17 410条数据按8∶1∶1的比例划分为训练集、验证集和测试集，以训练集中每种污染物的最大值为标准对训练集、验证集和测试集进行最大值归一化。

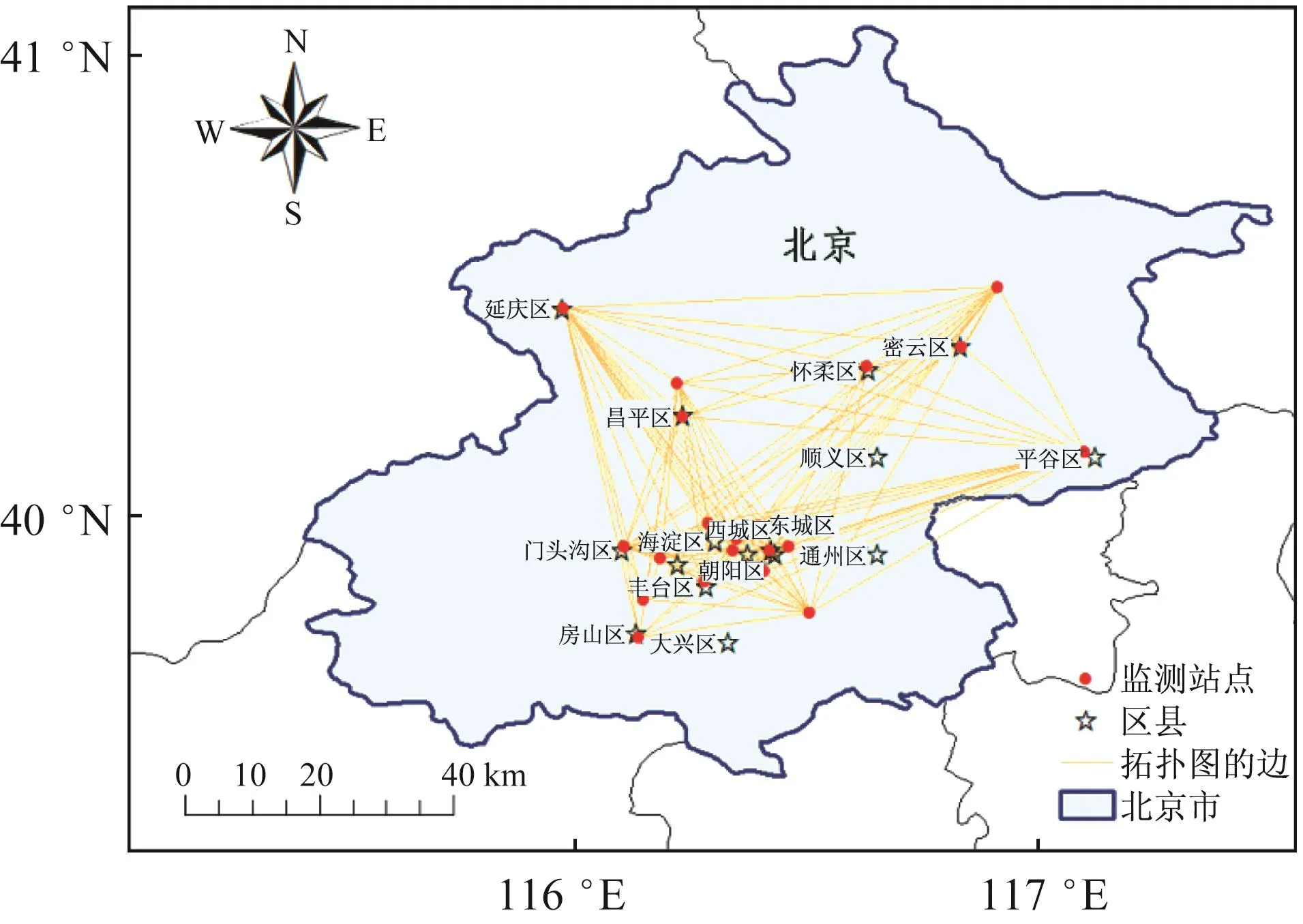
图6 空气质量监测站点分布及其拓扑图Fig.6 Distribution and topology of air quality monitoring stations

本文研究的PM2.5小时浓度多步预测属序列预测问题，也是回归问题，因此采用均方根误差（root mean squared error，RMSE）、平均绝对误差（mean absolute error，MAE）以 及 拟 合 指 数（index of agreement，IA）3个指标计算预测序列与实测序列之间的差，并用其评价预测效果。训练模型所用的超参数如表2所示。实验硬件环境为处理器为Intel（R）Xeon（R）CPU E5-2650 v4@2.20 GHz、GPU为GeForce GTX 1080 Ti、内存为64 GB的服务器，软 件 环 境 为 Python 3.6.0、PyTorch 1.0.0、CUDA 9.0。

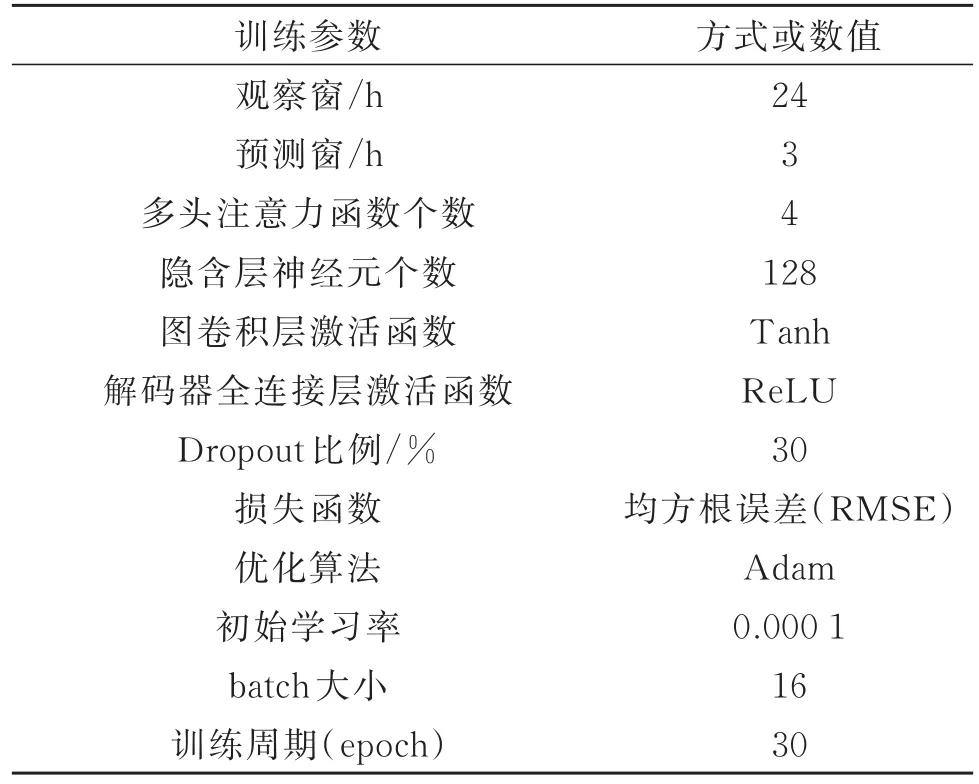
表2 训练模型超参数Table 2 Parameters of training model

2.2 实验结果分析

将训练数据组织为观察窗口24 h、预测窗口3 h的时间序列，分别训练GCN_Attention_Seq2Seq模型、GCN_Seq2Seq模型和Seq2Seq模型；将测试数据组织为观察窗口24 h、预测窗口分别为3，6，9，12，15，18 h的时间序列，用训练好的3个模型分别对6组测试数据进行预测。表3列出了3个模型在22个站点中的预测精度。由表3可知，无论是最好情况、平均情况还是最差情况，GCN_Attention_Seq2Seq模型的3项指标均为最优，3 h预测窗口的平均IA最高可达98.3%，GCN_Seq2Seq模型次之，Seq2Seq模型最差。GCN_Attention_Seq2Seq模型的平均RMSE比GCN_Seq2Seq模型低17.5%，比Seq2Seq模型低24.3%。结果表明，在Seq2Seq模型中，考虑空气质量监测站点之间的空间关系是必要的，且增加注意力机制可显著提高模型的预测精度。

表3 3个模型的预测精度Table 3 Prediction accuracy of three models

由于每个模型的最好情况、平均情况、最差情况对模型预测能力反映的趋势是一致的，图7为平均情况下随预测窗口的加长，3个模型的RMSE、MAE、IA指标变化情况。从3个指标的整体看，随着预测窗口的加长，GCN_Attention_Seq2Seq模型的误差与2个对照模型的分化越来越大，误差显著低于2个对照模型，当预测窗口小于12 h时，3个模型的RMSE均迅速升高，MAE缓慢升高，IA快速下降；当预测窗口大于12 h时，RMSE、MAE、IA均开始趋于稳定，趋于稳定后，Seq2Seq和GCN_Seq2 Seq模型的RMSE高居60及以上、MAE在40及以上，GCN_Attention_Seq2Seq模型的RMSE则在50左右、MAE在30左右。从IA单项指标看，随预测窗口的加长，GCN_Attention_Seq2Seq模型的IA始终保持在0.8以上，而Seq2Seq和GCN_Seq2Seq模型的IA则由最初的大于0.9分别降至0.6和0.7，结果表明，随着预测窗口的加长，GCN_Attention_Seq 2Seq模型的预测精度衰减率比未使用注意力机制的模型低得多，原因是编码器和解码器之间以及解码器内部使用了注意力机制，使得解码器不再只依靠编码器最后一个时间步的状态向量完成解码，而是在每个时间步上均考虑了编码器的所有输入向量，通过分配权重，加权求和得到解码器在当前时间步最关注的信息，从而降低了信息遗漏和记忆衰减。

为更清晰地说明注意力机制有助于减少信息遗漏和记忆衰减，本文提出以精度衰减率指标φ表示当前时间步的预测值与实测值的RMSE相较于前一时间步的增加幅度，即预测精度衰减的程度，计算式为

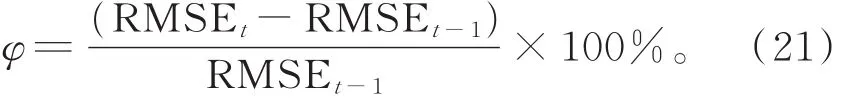
图7 3个模型的指标变化对比Fig.7 Comparison diagram of indicator changes of three models

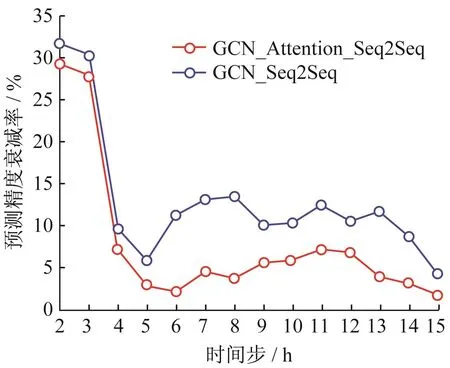
图8 当观察窗口为24 h、预测窗口为15 h时各个时间步的预测精度衰减率Fig.8 Prediction accuracy attenuation rate of each time step when the observation window is 24 h and the prediction window is 15 h

本文选取GCN_Attention_Seq2Seq和GCN_Seq2Seq模型，给予24 h的观察窗口，预测之后15 h内的PM2.5小时浓度，并计算预测窗口中每个时间步的精度衰减率φ，见图8。GCN_Attention_Seq2Seq模型在15 h预测窗口中的平均预测精度衰减率为6.32%，GCN_Seq2Seq模型在15 h预测窗口中的平均预测精度衰减率为11.62%，GCN_Attention_Seq 2Seq模型的预测精度衰减率显著小于GCN_Seq2 Seq模型，表明注意力机制对特征的自适应关注可实现对数据特征的有效利用，提高深度学习模型的应用效果。在15 h的预测窗口中，前2 h的精度衰减率较大，后续精度衰减率起伏较平缓，但GCN_Attention_Seq2Seq模型的预测精度衰减率始终低于GCN_Seq2Seq模型，且起伏更为平缓。GCN_Attention_Seq2Seq模型的预测精度衰减率起伏较为平缓的原因可能与自注意力机制发挥作用有关，预测窗口中已取得的预测结果为后续预测提供了更丰富的上下文信息。

以上分析足以表明，在PM2.5小时浓度多步预测中，注意力机制能减少信息遗漏和记忆衰减，降低预测精度衰减率，提高多步预测能力。

图9为2015年8月14日至2016年8月14日3个模型在云岗空气质量监测站点针对观察窗口24 h、预测窗口3 h，在预测窗口第一个时间步上的实测值和预测值折线图。由图9可知，GCN_Attention_Seq2 Seq模型的预测值和实测值的拟合度稍好于GCN_Seq2Seq模型，显著好于Seq2Seq模型。

3 结 语

考虑PM2.5小时浓度数据的时空相关性以及原始编码器-解码器模型容易发生记忆衰减，本文利用图卷积神经网络的对非欧式空间数据提取特征的能力以及注意力机制的自适应关注特征的能力，提出了融合图卷积神经网络和注意力机制的PM2.5小时浓度多步预测模型。以2015—2016年北京市22个空气质量监测站点的空气质量数据为样本，设计并训练了GCN_Attention_Seq2Seq，GCN_Seq2Seq，Seq2Seq 3种深度学习模型，在测试集上的验证结果表明，GCN_Attention_Seq2Seq模型的平均RMSE比GCN_Seq2Seq模型低17.5%，比Seq2Seq模型低24.3%；GCN_Attention_Seq2Seq模型在15 h预测窗口中的平均预测精度衰减率为6.32%，显著低于GCN_Seq2Seq模型的11.62%，证实了图卷积神经网络和注意力机制有助于提升PM2.5小时浓度多步预测的精度，注意力机制有助于减缓多步预测中的预测精度衰减。本文方法在时间序列上使用了注意力机制，取得了良好效果。下一步工作将重点研究注意力机制在空间特征提取中的作用。