基于线性规划建模的投资组合问题研究
2021-01-26周闻野黄瀚元徐邵阳
周闻野 黄瀚元 徐邵阳
1.人大附中朝阳分校; 2.北京海淀外国语实验学校; 3.橘郡美高
一、引言
投资理财是现代人增加收入的重要方式。在购买理财产品或者投资的过程中,需要投资人进行抉择。在本金一致的前提下,不同的组合会带来不同的收益。我们希望通过线性规划的方式,以建模的思想尝试预测投资组合中最优的投资组合选择,以达到收益最大化的目的。
投资组合问题的优化建模已在文献[1,2,3,4]中做过研究,可以看出纯粹的线性规划在简单的金融投资问题时适合使用,而在建模多目标,投资项目间不独立,或市场波动大的较复杂情况中需要进行特定变化。本文将研究线性规划在单一目标,平稳的市场中的应用。
据调查统计,我国国民中已有许多家庭购买储蓄理财及债权等投资产品,全国比例中少部分人选择股票,极少数人选择投资古玩、黄金等。可以看出,投资在国民中,尤其是较富有的国民中占有很重要的地位。我们认为,作为国民经济生活的重要组成部分,投资组合以求利益最大化的主题是被长期关注与探讨的。以符合现实的条件进行统筹规划,并且获得具有正确性的指导性投资建议是许多国民十分需要的。因此,研究投资组合的利益最大化具有重要的现实意义及应用价值。
二、问题描述
我们引用了9个国际上较为热门的理财和投资项目,设定每个项目的投资金额百分比作为决策变量。出于现实中投资者对于平衡性的要求,我们考虑了项目方差、投资品类等因素,并对这些因素做出了限制。为了使模型具有可操作性,我们以一些假设限制了市场上可能出现的状况。最终,我们的优化目标则是在以上条件下最大化年回报率。
这一模型中的数据均为真实信息,涉及到的可选项目、考虑因素及其约束均可以作为参数,就个人判断作调整,因此该模型的框架具有可拓展性及现实意义,可以协助解决实际问题。
三、模型假设和符号声明
(1)市场上只有9个投资项目。(1-9)
(2)所有投资项目没有最小投资额度。
(3)过去十年的股票趋势会持续到将来。
变量xi为投资项目i的资金量,以占总资金的百分比来计算。
四、模型建立和求解
(一)数据列表
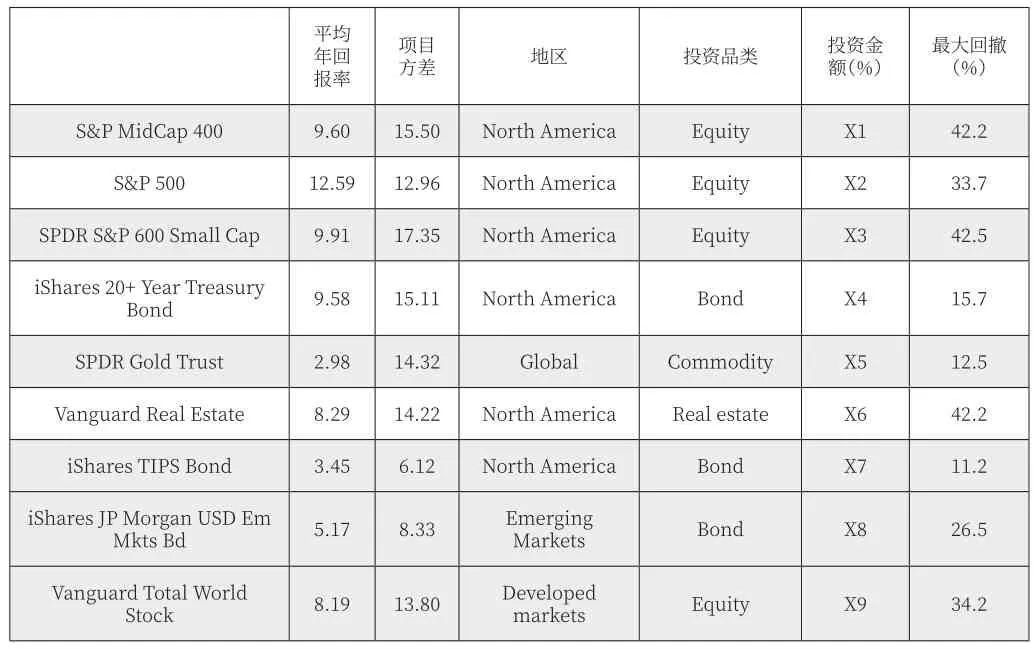
平均年回报率项目方差地区投资品类投资金额(%)最大回撤(%)S&P MidCap 400 9.60 15.50 North America Equity X1 42.2 S&P 500 12.59 12.96 North America Equity X2 33.7 SPDR S&P 600 Small Cap 9.91 17.35 North America Equity X3 42.5 iShares 20+ Year Treasury Bond 9.58 15.11 North America Bond X4 15.7 SPDR Gold Trust 2.98 14.32 Global Commodity X5 12.5 Vanguard Real Estate 8.29 14.22 North America Real estate X6 42.2 iShares TIPS Bond 3.45 6.12 North America Bond X7 11.2 iShares JP Morgan USD Em Mkts Bd 5.17 8.33 Emerging Markets Bond X8 26.5 Vanguard Total World Stock 8.19 13.80 Developed markets Equity X9 34.2
*该数据来自雅虎财经从2010.7.19到2020.7.17的每日股价
“最大回撤”指描述投资者可能面临的最大亏损,衡量资产价格从最高值到最低值的跌幅。用来衡量股票风险。(如:股票最高值为1000,最低到过500,最大回撤为50%)
最大化目标为平均年回报率,其中我们做了以下限制:
每类资产至少投资百分之五;
每类资产至多投资百分之四十;
最大回撤小于百分之三十;
在北美的投资不能超过百分之七十;
投资金额不超出总金额。
(二)线性规划模型
Maximize: 0.096X1 + 0.1259X2 + 0.0991X3 + 0.0958X4 +0.0298X5 + 0.0829X6 + 0.0345 X7+ 0.0517X8 +0.0819X9
S.t.
X1+x2+x3+x9>=0.05
x5>=0.05
x6>=0.05
X4+x7+x8>=0.05
X1+x2+x3+x9<=0.4
x5<=0.4
x6<=0.4
X4+x7+x8<=0.4
0.422X1+0.337X2+0.425X3+0.157X4+0.125X5+0.422X6+0.112X7+ 0.265X8+ 0.342X9<= 0.3
x1+x2+x3+x4+x6+x7 <= 0.7
x1+x2+x3+x4+x5+x6+x7+x8+x9 <=1
x1, x2, x3, x4, x5, x6, x7, x8, x9 >= 0
标准形式
Minimize: -0.096X1 - 0.1259X2 - 0.0991X3 - 0.0958X4 -0.0298X5 - 0.0829X6 - 0.0345 X7- 0.0517X8 -0.0819X9
S.t.
-X1-x2-x3-x9<=-0.05
-x5<=-0.05
-x6<=-0.05
-X4-x7+-x8<=-0.05
X1+x2+x3+x9<=0.4
x5<=0.4
x6<=0.4
X4+x7+x8<=0.4
0.422X1+0.337X2+0.425X3+0.157X4+0.125X5+0.422X6+0.112X7+ 0.265X8+ 0.342X9<= 0.3
x1+x2+x3+x4+x6+x7 <= 0.7
x1+x2+x3+x4+x5+x6+x7+x8+x9 <=1
x1, x2, x3, x4, x5, x6, x7, x8, x9 >= 0
(三)Python求解结果
使用python中的Linprog函数求解上线性规划模型。Linprog包是python语言中Scipy优化算法包中利用单纯形法解决线性规划问题的函数。函数求解形如:
Min cTx
s.t.Ax <= b
Aeqx = Beq
L <=x<=u
的线性规划问题,c,b,beq,l,u为向量,A为矩阵。算法使用的单纯形法由1947年丹齐克提出,是一个通过从可行解集的一个顶点出发沿着函数值下降的方向移动的迭代算法,能保证求出最优解,得到:

投资金额(%)X1 1.09 x 10-10 X2 0.15 X3 1.19 x 10-10 X4 0.4 X5 0.05 X6 0.15

X7 5.27 x 10-11 X8 3.37 x 10-10 X9 0.25
因为0.15+0.4+0.05+0.15+0.25=1,可以认为X1,X3,X7,X9的投资数额为计算偏差,则最佳策略为:
百分之15总金投资S&P 500,百分之40资金投资iShares 20+Year Treasury Bond,百分之5资金投资SPDR Gold Trust,百分之15资金投资Vanguard Real Estate,百分之25资金投资Vanguard Total World Stock,最大年收益率为百分之9.16。
五、模型解释
如上所述,项目1、3、7、8的结果可以作误差考虑,直接忽略。而2、4、5、6、9则(取近似)分别以15%、40%、5%、15%、25%投入资金,即可在限制条件下取得最大回报率。
根据以上结果我们可以看出,在对品类、地区、安全性都有限制的情况下,模型得出1、3、7、8不可选。现实意义上,1、3明显地具有较大的最大回撤(一日中最大的下降幅度),这意味着这两项投资项目有较大的可能出现意外,故不可选。7的年回报率过小,不适宜用于最大化收益,故不可选。8与4同属债券品类,但回报率与最大回撤均劣于4,故而4完全有理由占有绝大多数份额。
如果暂时抛开人为对投资品类做的最低要求,我们不难看出:总体上,总回报率更高,最大回撤更低的项目(大盘股、国债等)更值得多投入资金;反之,则不适合投资。这符合人们对市场的认识和生活经验。
除以上结论之外,模型还给出了优化后的最大年收益率。此项数据必须由算得的比例进行投资得到,这是一般人仅靠经验估测难以做到的,这意味着此模型对现实生活仍有特别的意义。并且,对个人资产的精准估计有利于对财产进行进一步精算,能够进一步扩大财政收益。
该模型也具有一些明显的不足。比如,我们在设定模型时所做的假设,例如未来的股票趋势与过去十年相同,不一定符合现实。模型一定会涉及到对实际情况的简化,如果需要在现实生活中使用,应尽量保证设定的假设符合实际,以提高预测的准确性。
