基于时空动态模型的鱼类和渔业发展的战略分布研究

杨 丽，袁子霞，吴 琪

(1.西南民族大学计算机科学与工程学院，四川 成都 610041；1，2.西南民族大学电气信息工程学院，四川 成都 610041)

全球气候的变化以及对可持续渔业管理的追求，促使人们更加需要了解海洋气候对重要鱼类行为的影响[1].海水温度是衡量海水环境的一个重要参数也是鱼类生活最重要的环境因子之一[2].现有研究大部分只是停留在环境的变化及改善措施，并未从与渔业公司最密切的经济角度出发，给出温度影响鱼群的具体程度与大致迁移方向以及其中带来的利益变化.

本文通过建立温度与鱼群数量的数学模型预测鱼群50年后迁移方向，在此基础上与经济结合分析，给出使渔业公司增加收益的具体措施.

1 背景

鱼类作为变温动物，它们的体温随环境水温变化而变化，并且鱼类对于温度变化的敏感性较一般陆生脊椎动物高，在鱼类的整个生活史上，水温是最重要的环境因子之一.

海洋渔业是苏格兰的传统产业，在国民经济发展中占据重要地位[3].鲭鱼是东北大西洋上的一种丰富的迁徙中上层鱼类，鲱鱼属于一种季节性鱼[4].两种鱼类的迁移状况与温度场相关.本文通过对这两种鱼类的时空动态研究预测未来变化趋势，以提出经济措施.

2 符号说明

文中所引用的变量和常量及其说明如下表1所示.

表1 符号说明Table 1 Symbol description

3 模型建立和分析

3.1 温度的预测

鱼类的生存位置很大程度取决于海水温度[5]，我们围绕苏格兰附近的海域选取了9个有代表性的测量点，找到每个点1971年至2018年共48年的海水温度统计数据，数据集是按时间排序的、随时间变化且互相关联的数据序列，即可看作时间序列.基于时间序列算法[6]建立未来50年海水温度的预测模型.

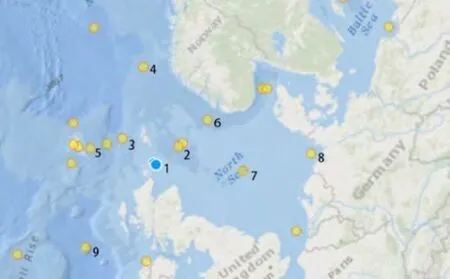
图1 参考点选择示意图Fig.1 Schematic diagram of reference point selection

结合ICES统计数据得到1971～2018年所选取9个参考点的温度数据.

对第一点时间序列数据进行平稳性检验，发现此时间序列的单位根为0，则样本数据为非平稳时间序列，经过差分后平稳，选用自回归移动平均模型(ARMA).

差分平稳:

计算自相关函数:

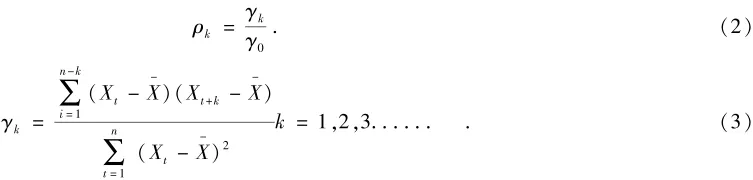
由公式(2)和公式(3)可得

利用MATLAB软件，可得样本数据自相关图像和偏相关函数图像(如图2所示):

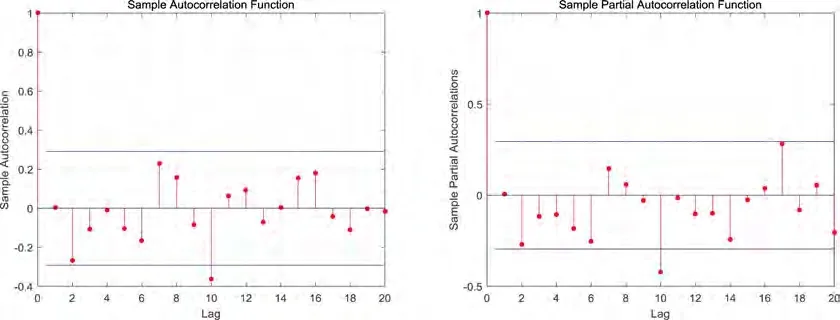
图2 地点1的自相关图和偏相关图Fig.2 Function of site 1 image

其余八个点均通过相同处理方式预测五十年后的海水温度.

使用时间序列模型对选取的九个参考点预测分别得到每个点五十年后的海水温度，如下图3所示.并根据上述分析，可以预测出50年的9个参考点的温度.数据如表2所示.

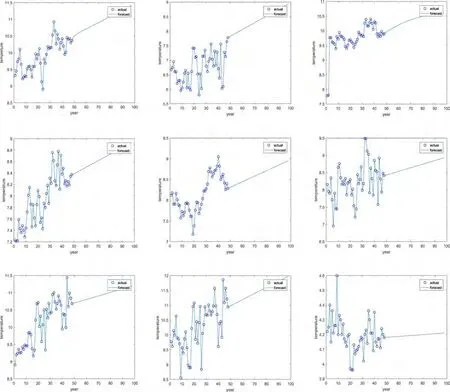
图3 未来50年9个参考点的温度预测图Fig.3 Temperature prediction chart of 9 reference points over the next 50 years

表2 温度预测结果Table 2 Temperature prediction results

3.2 鱼群数量的预测

利用苏格兰政府每年渔业统计数据，统计与温度对应年份鲭鱼和鲱鱼的捕获量.利用MATLAB进行关系拟合，得到温度和数量之间的二维拟合关系.并由函数拟合得到的渔业产量与海洋温度的关系式如图4所示.

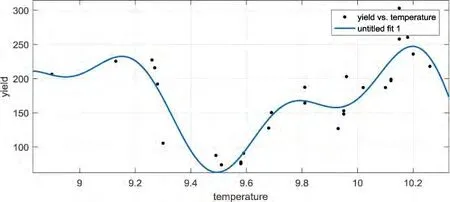
图4 温度和数量之间的二维拟合关系Fig.4 Temperature and yield diagram

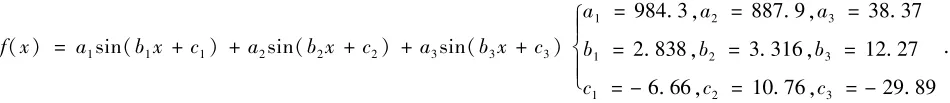
根据图4的分析，可以预测50年后9个参考点的产出量.这些数据显示在下表3中.

根据该模型，得到50年后的鱼群位置分布图，如图5所示，鱼群向东北方向移动.

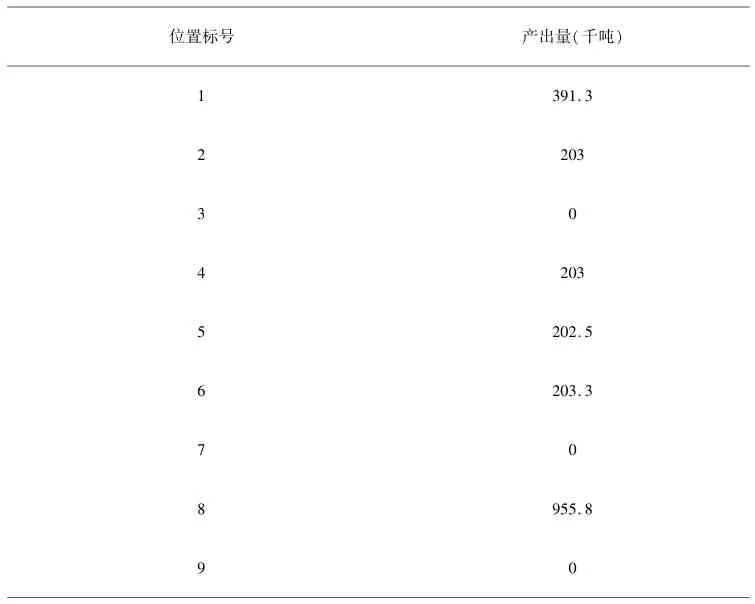
表3 50年后9个参考点的产出量的预测结果Table 3 Catch at reference points after 50 years

图5 50年后的鱼群位置分布图Fig.5 Distribution map of fish school after 50 years

3.3 发展状况的预测

为了预测在苏格兰领海内两种鱼迁移给渔业公司所带来的经济影响，我们建立稳定状态模型，结合鱼群捕捞量和经济收支[7]考虑利益.

某时刻下，渔场鱼群的数量为x(t)，固有自然增长率r和环境容许的最大承载量N[8]，由logistic模型可以得到，x(t)满足

考虑捕捞系数E，单位时间的捕捞量关系如下:

由于渔场鱼群的数量是在该时刻是一定的，因此单位时间捕捞量为一常数，称其为特定的捕捞策略，满足Schesfer模型[9]:

当E＞r时，x2＜0，此时有x·＜0，此时鱼量将逐步减少至0，不符合最佳捕鱼量和最大经济效益的要求，即对应最坏的捕鱼情况.

当E＜r时，x2＞0，x=x2为平衡稳定解，在该点处能够使得捕鱼量最大，产量稳定在Ex2，即对应最佳的捕鱼情况.

假设每吨鱼的单位售价为p，每条出海渔船的费用为c，则

t时间内捕鱼最大收入为P，满足:

t时间内最大捕鱼支出为Q，满足:

由公式(10)(11)可知:t时间内最大利润为R，满足:

在最佳情况下，结合捕捞量最大和经济效益最大化的要求，可知当鱼量满足在x=x2下，满足约束条件x=下，利润的最大值Rmax即为所求，即当E满足时，上式成立，此时

最大利润下渔场稳定捕捞量为

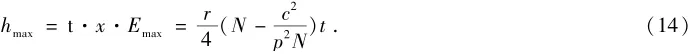
最大利润为

根据苏格兰政府渔业统计数据可知2009～2018这十年间苏格兰政府所允许的最大捕鱼量，且近十年内大西洋靠苏格兰海域内鱼群的环境最大承载量为420 000吨.

近似认为苏格兰政府所允许的最大捕鱼量即为产量，将数据代入公式(9)可得，，推知tmax=4.9872年，tmin=2.6446年.

由此可知，在最佳情况下，即产量最大，Hmax=523 656吨，持续时间约为5年；最坏情况下，即产量最小，Hmin=277 679吨，持续时间约为2～3年.

3.4 经营策略的提出

策略1：转移资产：

为了使出海渔船的距离成本减小，耗油量减小，使得成本开支减小[10].可以采取将部分捕捞公司的资产从位置1转移到位置8附近.选取北海海湾附近的挪威港口，当渔船靠近这些港口后，直接将渔获物售卖给当地的渔民和商贩，建立长期的合作.

策略2：改变渔船类型：

小型渔船具有体型小、易操作的特点，更适合海岸线长、复杂的捕捞作业环境[11]，并且可以在没有陆上支持的情况下运行一段时间，以确保获物的新鲜度和高质量.

策略3：捕捞渔船采用生物柴油：

采用生物柴油的方式，减小经济成本实现绿色可持续发展.综合考虑生物柴油比普通柴油的燃油费用差和维修费用差，以及柴油机的改造成本.[12]结合当代节能减排理念，碳交易机制[13]的出现也能为使用生物柴油机的捕捞公司带来收益.

策略4：跨界渔业合作：

在总成本最小化下，通过与挪威和德国之间合作的渔业经济收益大于单独国家进行捕捞的经济收益，合作能使得经济收益最大化[14].

4 结束语

海洋温度变化作为生物多样性的重要参考因素，本文采用时间序列模型和稳定状态模型对苏格兰海域温度、鱼群数量数据进行分析，并预测鱼群未来的生存发展；结合成本效益分析，从经济收益等角度为渔业公司提供可行性的经营策略.预测结果显示两种鱼类的迁移情况和历史情况中鱼群迁移的趋势相近，预测温度显示海水温度有上升的趋势与现实情况吻合，模型预测结果的准确度较好.综上所述，本文采用的算法模型考虑了海水温度、鱼群生长规律、经济发展、财政赤字[15]等影响因素，将误差减小到最低，最后得到较好的结果.而随着时间推移，在自然灾害或人类行为等因素的干扰下，实际情况还有很多无法预测的新特点，这将是之后的研究方向与改进之处.