品高考试题 揭数学本质*

戚有建 石青慧 (江苏省扬州中学 225009)

很多高考题看似平常，实际上却很不平常，意蕴丰富，都是经由命题专家精心思考编制出来的，有很大的教学价值和研究空间. 本文从2020年全国卷的一道高考解析几何题出发，首先探究问题的解法，再对问题进行推广和类比研究，最后研究问题的深刻背景及应用．

1 考题展示

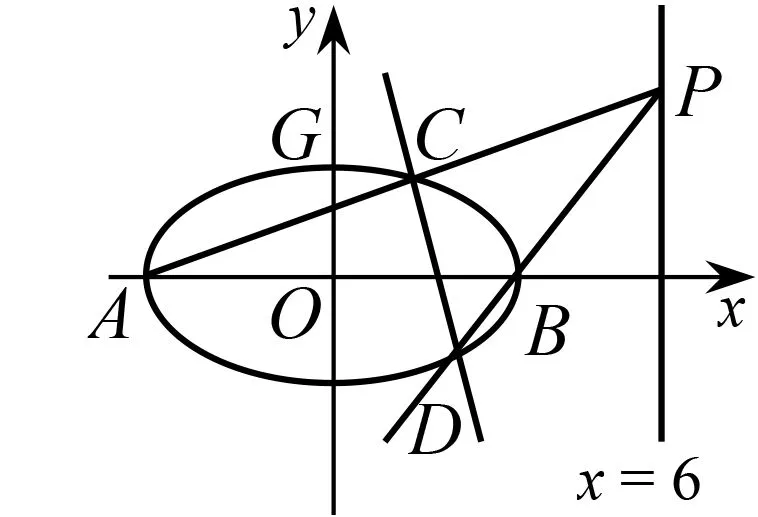
图1

(1)求椭圆E的方程；

(2)证明：直线CD过定点．

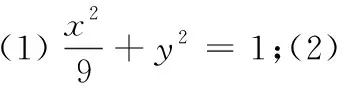
点评本题是2020年全国卷Ⅰ理科第20题，是试卷的压轴题，也是选拔题，与2010年江苏卷第18题相似度很高. 第(1)问对学生来说很容易上手，化简向量关系式求出基本量a即可;第(2)问证明直线过定点，意在考查用方程来研究曲线的性质，即用代数方法(坐标法)来研究几何问题(定点问题). 本题看起来很平凡，实际上却是平而不凡，有一定难度和区分度，也有很大的研究价值，我们重点研究第(2)问.

2 解法研究

除了文[1]中刘小树、陈琳两位老师给出的五种解法外，我们再给出构造曲线系的证法：

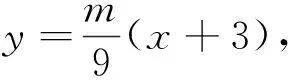
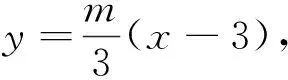
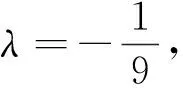
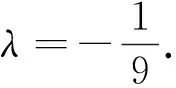
3 推广研究

证明过程类似，从略．

4 类比研究

将结论1中的“椭圆”改为“双曲线”，结论成立吗？研究后发现仍然成立，即有下面的结论：

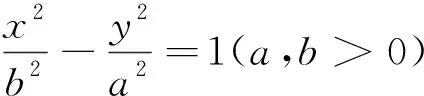
说明 将结论1中的“椭圆”改为“圆”，结论也成立，因为圆可以看作是椭圆的特殊情况.

5 背景研究

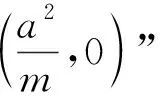
(1)如图2，设P为不在圆锥曲线上的点，过点P引两条割线交圆锥曲线于点E,F,G,H，设EG与FH交于点M，EH与FG交于点N，则称MN为点P对应的极线． 同理，称PN为点M对应的极线，PM为点N对应的极线．

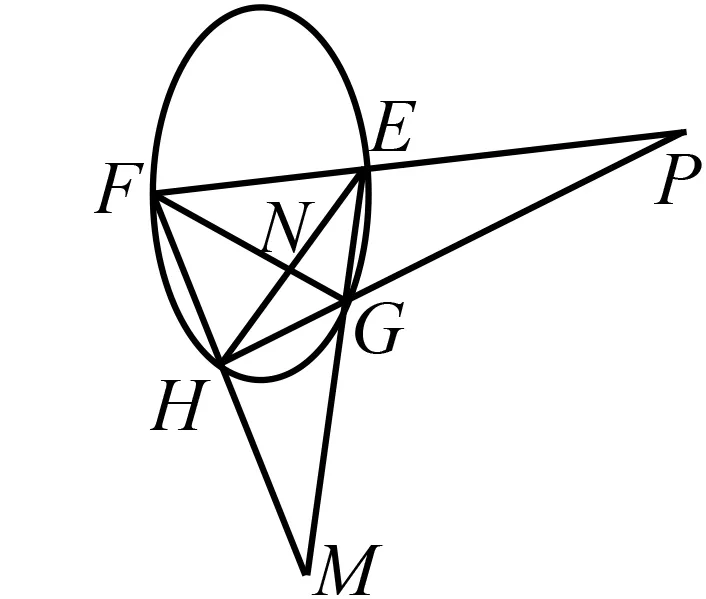
图2

现在我们用极点极线知识来解释这道高考题，过程如下：

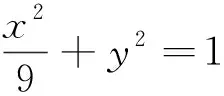
6 背景应用

笔者做了一些研究，发现很多高考解析几何题(定点定值问题)都与极点极线有关，都是以极点极线作为命题背景． 例如：

试题1(2011年四川卷理科21题)如图3，已知椭圆的两个顶点A(-1,0),B(1,0)，过焦点F(0,1)的直线l与椭圆交于C,D两点，并与x轴交于点P，直线AC与直线BD交于点Q．

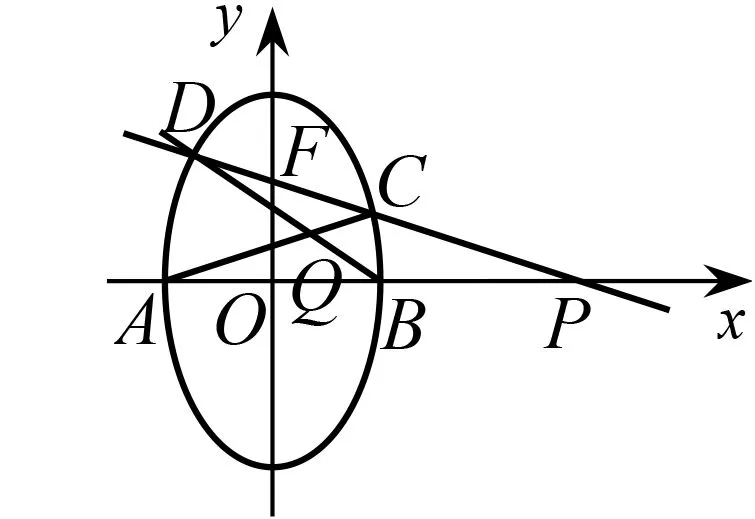
图3

(1)求椭圆的标准方程；

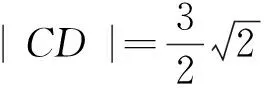
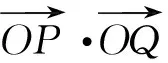
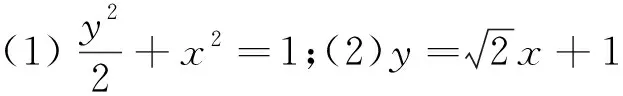
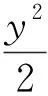
试题2(2012年北京卷理科19题)已知曲线C：(5-m)x2+(m-2)y2=8(m∈R)．

(1)若曲线C是焦点在x轴上的椭圆,求m的范围;

(2)设m=4,曲线C与y轴的交点为A,B(点A位于点B的上方),直线MN与曲线C交于不同的两点M,N,直线AN与直线BM交于点G，求证:A,G,N三点共线.

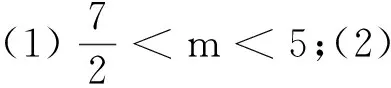
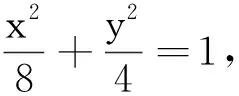
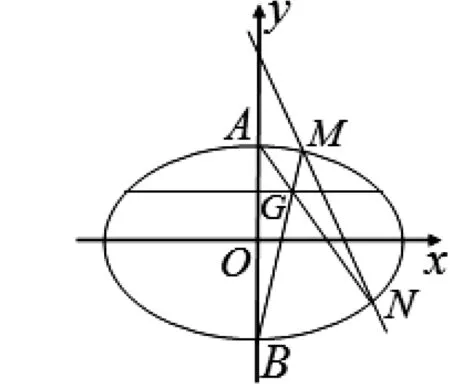
图4