干湿循环对高填方路堤边坡稳定性影响研究
2021-01-23孙宏磊赵家琛
孙宏磊,吕 江,赵 晖,赵家琛
(1.浙江大学 建筑工程学院,浙江 杭州 310058;2.浙江工业大学 土木工程学院,浙江 杭州 310023;3.杭州交通投资建设管理集团有限公司,浙江 杭州 310024)
随着我国公路建设向山区延伸,高填方路基越来越常见,其沉降变形和稳定性成为公路安全的关键[1-3]。千黄高速公路浙江省淳安段工程中,库湾区填方路堤共有16 处,其中最大填筑高度55 m。根据历年水文资料统计分析及现场水文调查,千岛湖水库常年枯水位高程约97 m,高水位约107 m,季节性水位变化形成了高度10 m左右的消落带。周期性的干湿交替作用会引起路基的细颗粒冲蚀,造成填方土体的力学性质劣化,这将降低路堤边坡的稳定性,从而影响其长期服役性能。
近年来,一些学者针对干湿循环作用下岩土体的力学性质进行了试验研究。邓华锋等[4]、Zhang等[5]、刘新荣等[6]、Luo等[7]、徐志华等[8]以砂岩、泥岩为对象的试验结果表明:干湿循环使岩土体强度显著衰减,5~6 次之后参数趋于稳定,此外黏聚力的劣化作用大于内摩擦角。同时,部分学者对干湿循环以及水位升降对边坡稳定性的影响进行了研究。邓华锋等[9]采用室内快剪试验,研究了三峡水库岸坡消落带岩土体在0~7 次干湿循环后的抗剪强度变化及其对岸坡稳定性的影响,发现前4 次干湿循环作用造成的抗剪强度衰减非常明显,相应的安全系数从1.063降低到0.895。但仅用安全系数评价边坡稳定性,具有一定局限性。周世良等[10]为研究泥岩库岸的稳定性规律,用常规三轴压缩试验测试了经过不同干湿循环次数的抗剪强度参数,并采用极限平衡法得到泥岩库岸中值安全系数,用1 000 次蒙特卡洛模拟得出可靠度的时变规律,但模拟次数少,所得结果离散性较大。Wu等[11]通过改变水头大小讨论了水位变化下的三峡库岸稳定性,分别用极限平衡法和10 000 次蒙特卡洛模拟计算了安全系数及可靠指标,但该方法计算效率较低。这些研究成果为合理分析库区路堤边坡的长期稳定性提供了较多试验依据。但综合目前的成果来看,大部分学者未考虑地基土参数的不确定性,仅采用单一的安全系数标准来评判边坡稳定性,而实际工程的复杂性导致安全系数无法定量描述边坡的安全度,如黄陵—延安高速公路沿线边坡设计安全系数均大于1.30,却仍有部分边坡失稳[12],由此可见:增大安全系数不一定能提高边坡稳定性,且较大的安全系数又会造成浪费。可靠度分析是处理边坡不确定性问题的一种有效方法,能得到可靠指标和失效概率等更有意义的结果。也有部分学者使用蒙特卡洛法进行可靠度分析,该法虽然简单易行,但要得到精确的可靠指标所需的计算量很大,计算效率低。因此,笔者在前人研究的基础上,以千岛湖库区路堤边坡为研究对象,定量考虑参数不确定性以及各变量之间的相关性,以响应面法为基础建立考虑干湿循环作用的路堤边坡可靠度分析框架,计算效率显著提高,结合确定性方法和可靠度方法,根据安全系数和失效概率联合评价路堤边坡稳定性,为同类工程提供稳定性评价参考。
1 确定性分析
1.1 有限元强度折减法
强度折减法本质上是通过一个折减系数Fs,对土体抗剪强度指标黏聚力c和内摩擦角φ进行折减,通过有限元计算边坡的应力、应变及位移场。以迭代求解的不收敛[13]作为路堤边坡的失稳判据,设置了节点不平衡力与外部荷载之比的收敛容差为5×10-3,不断增大折减系数Fs的值直至边坡发生破坏,将此极限状态对应的折减系数Fs定义为边坡稳定的安全系数。对土体抗剪强度指标黏聚力c和内摩擦角φ的折减计算式分别为
(1)
(2)
式中:cr,φr为折减后的强度参数。
1.2 模型参数
如图1所示,选取溧阳至宁德国家高速公路浙江省淳安段QHTJ-03合同段最大填方高度处路基断面,根据勘察报告确定材料参数,其中干湿循环部分为碎石土,其抗剪强度参数[9]如表1所示。表1中的参数为特定次数干湿循环试验后的原状土经直剪试验所得,其中一次干湿循环过程为自然浸泡饱水48 h后,采用恒温鼓风干燥箱在35 ℃下进行时长48 h的干燥处理。
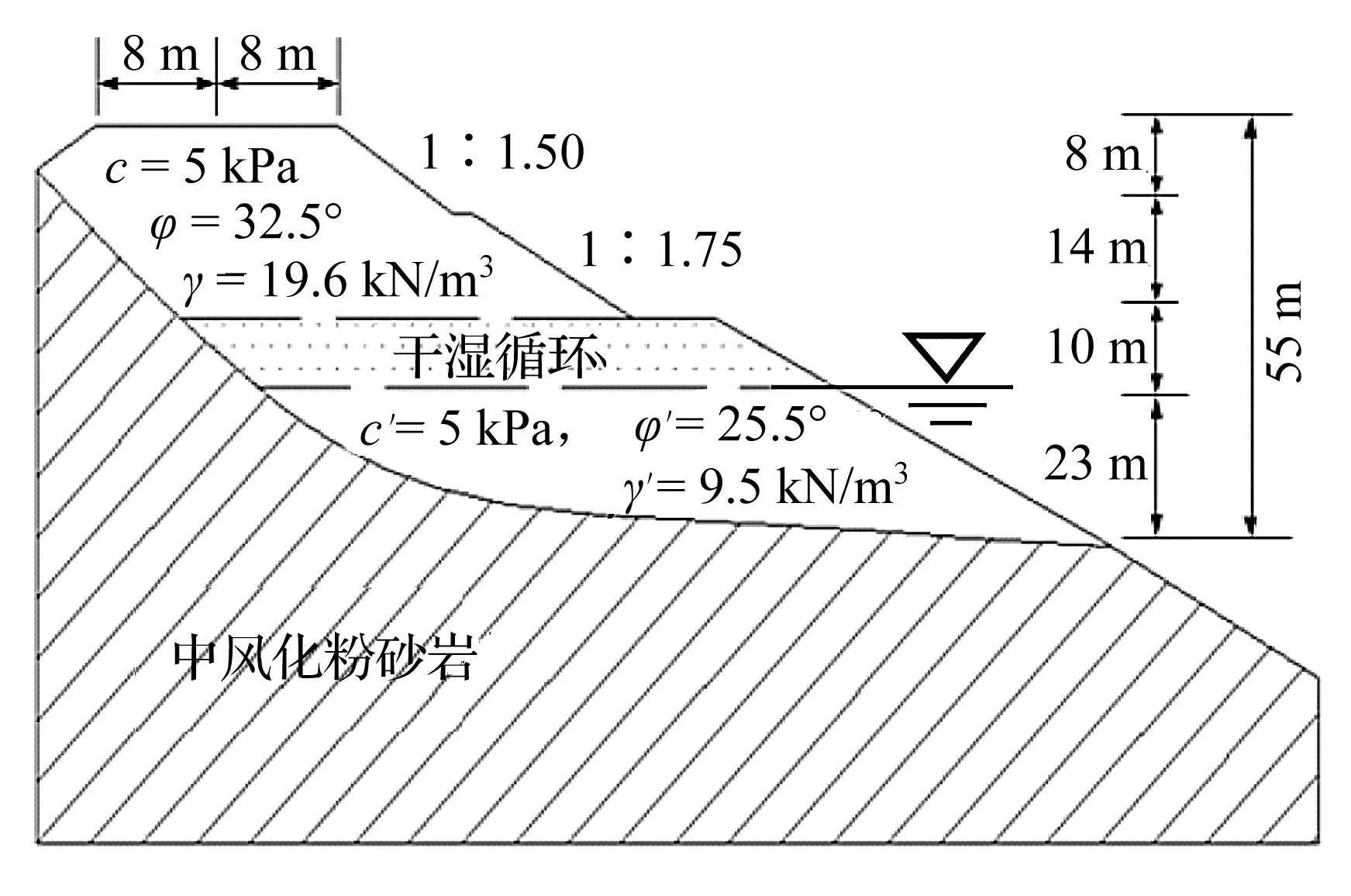
图1 高填方路堤边坡断面图

表1 不同干湿循环次数下抗剪强度参数
在ABAQUS中建模,其中水位以下土体参数取有效应力状态值,采用Mohr-Coulomb屈服准则的理想弹塑性模型,CPE8R型网格,有限元模型如图2所示。将上述参数作为均值μ进行确定性分析得到中值安全系数。
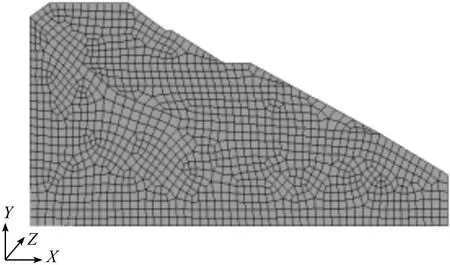
图2 路堤边坡有限元模型
2 可靠度方法
为了考虑边坡问题中的不确定性,采用可靠度方法,以得到可靠指标和失效概率,进而更准确地评价路堤边坡的稳定性。国内外众多学者提出了许多可靠度计算方法[14-17],如一次二阶矩法、高阶矩法、蒙特卡洛及其改进方法等。此外,响应面法(Response surface method,简称RSM)常用于没有显式功能函数的可靠度问题,大量研究表明响应面法作为边坡可靠度计算方法是较为高效的[18-20]。
最常见的响应面函数往往为二次多项式,为了在确保计算精度满足要求的前提下提高计算效率,使用不含交叉项的二次多项式,则具有q个变量的二次响应面函数模型可表示为
(3)
式中:λ0,λi,λii为待定系数,共2q+1个。
将各土层的抗剪强度参数作为变量,q=6,则需要13 个试验点来确定待定系数。使用中心复合设计取样方法,将各试验点代入有限元中,利用强度折减法计算安全系数,从而求解响应面函数,再采用验算点法计算路基稳定的可靠度。为了考虑随机变量的非正态分布以及变量之间的互相关性,分别采用当量正态化和正交变换进行处理。最后由可靠度与失效概率的关系求得失效概率。
2.1 取样方法
考虑到二次响应面法在中心点附近具有足够精确的近似模拟,试验点应位于变量均值附近,因此使用中心复合设计取样方法[21]求解响应面函数,包括2q个轴向点和一个中心点,轴向点反映了模拟区域的大小。在q维向量空间中,轴向点设计为
轴向点到设计中心的距离计算式为
α=2q/4
(4)
因此中心复合设计的取样点为轴向点xi和中心点xj可分别表示为
xi=μXi±ασXi
(5)
xj=μXj
(6)
根据所建模型取q=6,共有12 个轴向点和一个中心点,式(5)中的标准差可表示为
σ=μ·cv
式中cv为参数的变异系数。为了最大限度地考虑参数不确定性,cv取相关资料[22-24]给出范围的最大值,内摩擦角与黏聚力的变异系数分别取0.2和0.4。
2.2 可靠度求解方法
在得到路基稳定性的功能函数g(X)后,其可靠度指标通过验算点法来计算。基本原理是将功能函数在失效面上进行Taylor展开,利用随机变量的前二阶矩求解可靠度指标。以下分别介绍随机变量非正态分布以及变量之间存在互相关性时的处理方法。
2.2.1 考虑非正态分布随机变量的当量正态化
常见的土性指标作为随机变量,一般可用正态分布或对数正态分布来描述,内摩擦角φ和黏聚力c均取对数正态分布[18]。当基本变量X中含有非正态随机变量时,运用验算点法需要进行当量正态化处理。


(7)
(8)
对于X>0,对数正态分布的概率密度函数为
(9)
式中:λ,ζ分别为lnX的均值与标准差,其计算式分别为
(10)
(11)
2.2.2 考虑随机变量相关性的正交变换

(12)
2.3 响应面迭代求解方案
为提高可靠度计算的精度,也就是提高验算点附近的响应面模拟精度,则抽样点应靠近验算点,可通过迭代来实现,具体计算步骤如下:
步骤1使用中心复合设计取样方法,将μX作为样本点中心生成13 个样本点,包括轴向点和中心点,式(4)中的α=23/2。
步骤2再通过有限元强度折减法,在各个样本点处得到安全系数Fs,以计算出功能函数的响应值g=Fs-1,进而解方程求出待定系数,得到响应面函数,即每计算一次响应面需要进行13 次有限元分析。
步骤3采用当量正态化、正交变换与验算点法结合的方式计算验算点x*和可靠度指标β。
步骤4下一步迭代时,新的样本点中心xc可通过线性插值得到
(13)
式中x*是上一步求得的验算点,使用xc和xci±ασXi构成新的样本组合。
步骤5重复步骤2和步骤3,直到前后两次‖β‖之差<ε,取ε为0.001[19]。
3 计算流程
通过Matlab,Python与ABAQUS三者的交互,建立接口将路堤边坡稳定性分析与可靠度分析结合起来,形成可靠度计算框架。图3给出了可靠度框架与计算流程。

图3 可靠度计算框架
4 计算结果及分析
从图4中可以看出:考虑干湿循环部分强度参数劣化时,路堤边坡的安全系数明显减小,总体趋势与强度参数劣化规律基本一致。在前4 次干湿循环作用中,抗剪强度参数劣化程度约占总劣化度的75%,边坡安全系数减小了8.0%,4 次干湿循环作用之后,边坡安全系数减小的趋势变缓,仅降低2.6%。根据《公路路基设计规范》第7.18.3条及表3.6.11,结合千岛湖水库工况及土体试验指标,要求路堤稳定设计安全系数≥1.25。而经过7 次干湿循环作用,安全系数已从1.320降低到1.182。也就是说路堤边坡的安全系数随着干湿循环作用次数的增加,将不满足设计要求,此时仅仅根据单一的中值安全系数很难准确评判路堤的长期稳定性。
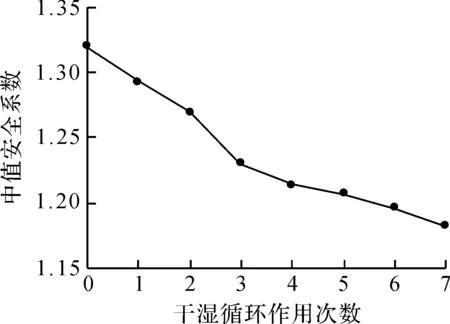
图4 中值安全系数与干湿循环作用次数的关系
图5为不同次数干湿循环作用后路堤稳定性的可靠度变化情况,且列出了4 种不同相关系数下的结果。所有结果的迭代均在20 次以内,计算效率高。由图5可看出:可靠度的变化趋势同样与抗剪强度参数劣化规律对应,但其降低幅度明显大于安全系数。抗剪强度参数相关性未被考虑时,前4 次干湿循环过程可靠度降低了25.1%,之后降低4.1%。由图6同样可得:4 次干湿循环作用后的折线间距较小,即可靠度变化幅度减小。干湿循环作用次数相同时,参数的负相关性越大,可靠度越高,且ρ=-0.75的结果相比于参数独立的情况,可靠度增加率均超过了40%。由此可见:无法考虑参数相关性的确定性方法会大大低估边坡的安全性。

图5 不同相关系数下可靠度与干湿循环作用次数的关系

图6 不同次数干湿循环作用下可靠度与相关系数的关系
由图7可见:失效概率随干湿循环作用次数的变化趋势与可靠度相反,同样地在4 次干湿循环作用后,其增速变缓。在考虑参数负相关性时,失效概率表现出极大的差异,变量独立的结果为ρ=-0.75的15 倍之多,可见在边坡稳定性分析中,参数之间的相关性不可忽视。从失效概率的角度来分析,根据表2可知:所有失效概率均小于5%,可知该路堤边坡处于稳定状态[28]。因此,在确定性分析所得安全系数已不满足设计要求的情况下,结合可靠度分析结果,可以对此路堤边坡做出较为准确的评价,认为该路堤边坡在经历多次干湿循环作用后保持稳定。

图7 不同相关系数下失效概率与干湿循环作用次数的关系
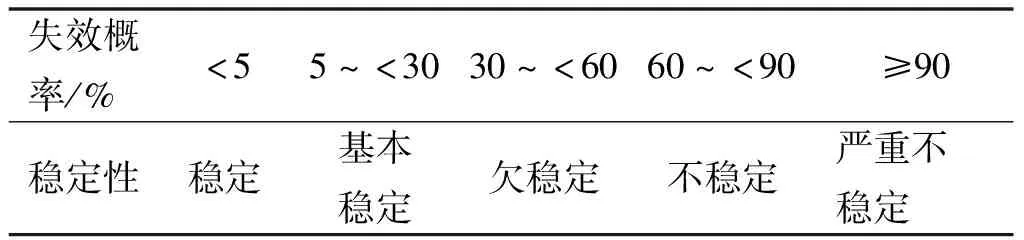
表2 不同失效概率对应的边坡稳定性
5 结 论
将有限元强度折减法与可靠度方法相结合,以响应面法为基础建立了考虑干湿循环作用的路堤边坡可靠度分析框架,该方法能定量考虑参数不确定性以及各变量之间的相关性,且计算效率高。以千岛湖库区路堤边坡为研究对象,计算结果表明:库区路堤稳定性与土体的抗剪强度紧密相关,在前4 次干湿循环作用过程中,抗剪强度参数降低幅度十分明显,之后减小趋势趋于平缓;经过7 次干湿循环作用,安全系数已降低至不满足设计要求,仅通过确定性方法所得结果评判路堤的长期稳定性存在局限性;路堤边坡稳定性的可靠度变化趋势与安全系数一致,但其降低幅度明显大于安全系数;失效概率与可靠度一一对应,其变化趋势与可靠度相反,根据所得最大失效概率对该路堤边坡进行评价,认为其在经历多次干湿循环作用后能保持稳定;干湿循环作用次数相同的情况下,参数的负相关性越大,可靠度越高,因此简单地认为变量之间相互独立将严重低估边坡的安全性。该方法可为同类工程提供稳定性评价参考。
