一种老年人热舒适仿真模型

杨玉兰，李 洋，邰惠鑫，刘抚英，倪彤元

(浙江工业大学 设计与建筑学院，浙江 杭州 310023)

随着我国城镇化与人口老龄化的快速发展，老年人群体成为许多学者的研究对象。老年人心理和生理都有其特殊性，随着年龄的增长，老年人生理机能逐渐退化，新陈代谢减缓，对热环境变化的适应能力和调节能力逐渐减弱[1-3]。经典热舒适预测PMV模型被广泛应用于建筑热环境预测，并被拓展运用于不同空间进行热舒适预测[4-5]。研究表明采用传统热舒预测模型PMV对老年人进行热舒适预测存在精度差、考虑因素少等不足[6-7]。老年人热舒适仿真涉及信息维度众多，是一个多维度非线性仿真课题。近年来，由于机器学习具有高维度信息处理能力强、预测精度高等优点，机器学习被探索性地运用于热舒适预测。Kim等[8]研究6 种预测个人热感觉的机器学习模型，发现6 种模型的平均预测精度均高于PMV模型预测精度。杜晨秋等[9]引入CART决策树方法对6 个城市居住建筑中的人员热舒适进行预测，达到较高的预测精度。Breiman[10]于2001年提出随机森林算法，采用决策树作为基分类器，随机生成多棵决策树进行仿真建模。随机森林模型能有效处理非线性多维数据、具有预测精度高、抗噪能力强和适应范围广等优点[11]。采用传统的随机森林进行预测建模的不足之处主要表现在以下3 个方面：一是单一节点分裂算法存在节点优化分裂措施贫乏的不足；二是未区别对待生长效果不同的决策树，在传统随机森林的分类结果投票中，生长效果差的决策树和生长效果好的决策树拥有同样的投票能力；三是传统随机森林在投票过程中未考虑到出现相同票数的情况，不利于分类。针对随机森林以上3 个方面的不足，笔者提出一种基于改进随机森林的老年人热舒适仿真模型。

1 基于改进随机森林的老年人热舒适仿真理论模型

笔者提出的老年人热舒适仿真理论模型采取以下措施改进传统随机森林模型。将节点分裂算法运用于老年人热舒适预测训练样本进行实验仿真，得到C4.5和CART节点分裂算法在老年人热舒适预测数据集的预测精度；根据节点分裂算法的预测精度，为C4.5和CART节点分裂算法分配权重，并构建混合节点分裂算法，旨在获得最优节点分裂规则，以此构成随机森林基分类器；对决策树赋予量化权值，采用决策树加权投票策略，使得决策树具有与其生长效果相应的投票能力，同时解决了出现相同票数的情况，提高了随机森林的分类正确率。基于改进随机森林的老年人热舒适仿真理论模型主要有6 个步骤。

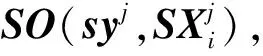
(1)

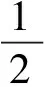
(2)

式中：Info(S)为数据集S的信息熵；|sk|为数据集S中老年人热舒适等于第k个类别的样本数；|s|为数据集S的样本数；K为老年人热舒适类别总数。

将S根据因素xi的因素值分类，分类子集数目等于因素xi的因素值的个数，按照因素xi计算S热舒适分类的信息熵为

(3)

式中：Info-xi(S)为按照因素xi对S进行热舒适分类的信息熵；R为数据集S中因素xi所具有的因素值的个数；r为因素xi的第r个因素值；|sr|为数据集S中因素xi的因素值等于第r个因素值的样本数；Info(Sr)为数据集S中因素xi的因素值等于第r个因素值的数据集的信息熵。

按照因素xi计算S热舒适分类的信息增益量为

Gain(xi)=Info(S)-Info-xi(S)

(4)

式中Gain(xi)为按照因素xi对S进行热舒适分类的信息增益量。

按照因素xi计算S热舒适分类的分裂信息比率为

(5)

式中SplitInfo(xi)为按照因素xi对S进行热舒适分类的分裂信息比率。

按照因素xi计算S进行热舒适分类的信息增益率为

(6)

式中GainRatio(xi)为按照因素xi对S进行热舒适分类的信息增益率。

选择信息增益率值GainRatio(xi)最大的因素作为决策树分裂规则，将S按照分裂因素的因素值个数分裂为多个子节点；将子节点数据集作为根节点数据集S，重复以上迭代步骤进行决策树分裂，直到完整的决策树构建完成为止；随机抽取老年人热舒适预测特征数据集SO中一定数量的样本数据作为决策树分裂算法赋权数据集C，将数据集C输入构建完成的决策树进行仿真测试，得出基于C4.5分裂算法构建决策树运用于老年人热舒适预测的准确率P1。

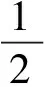
(7)

式中：Gini(S)为数据集S的基尼指数；|sk|为数据集S中老年人热舒适等于第k个类别的样本数；|s|为数据集S的样本数；K为老年人热舒适类别总数。

将数据集S根据因素xi是否等于第r个因素值划分成S1和S2两个部分，S1为S中因素xi等于第r个因素值的数据集，S2=S-S1，数据集S根据因素xi是否等于第r个因素值进行划分的基尼指数为

(8)

式中：Ginisplit(S,xi(r))为将数据集S根据因素xi是否等于第r个因素值进行划分的基尼指数；|s1|，|s2|分别为数据集S中因素等于第1个类别和第2个类别的样本数。

选择划分基尼指数Ginisplit(S,xi(r))最小值的因素及对应的因素值作为决策树的分裂规则，将S分裂为2 个子节点；将子节点数据集作为根节点数据集S，重复以上迭代步骤进行决策树分裂，直到完整的决策树构建完成为止；随机抽取老年人热舒适预测特征数据集SO中一定数量的样本数据作为决策树分裂算法赋权数据集C，将数据集C输入构建完成的决策树进行仿真测试，得出基于CART节点分裂算法运用于老年人热舒适预测的准确率P2。

步骤4将P1和P2按照其在算术和中占的比例分别赋予C4.5节点分裂算法和CART节点分裂算法相应的权重β1和β2。

Φ(S,xi(r))=β2Ginisplit(S,xi(r))-

β1GainRatio(xi)

(9)

式中Φ(S,xi(r))为依据因素xi是否等于第r个因素值将S进行分类的混合分裂指标。

选取混合分裂指标Φ(S,xi(r))最小值的因素和因素值将S分裂为两个子节点；将子节点数据集作为根节点数据集S，重复以上迭代步骤进行决策树分裂，直到构建完整的决策树为止；假设重复以上操作P次，形成P棵决策树T1，T2，…，TP，以此组成基于混合分裂算法决策树的老年人热舒适预测随机森林；将决策树赋权数据集D2中的样本分别输入到P棵决策树中，得到每棵决策树的老年人热舒适分类正确率ωp(p=1,2,…,P)，按照每棵决策树的分类正确率为决策树赋权。

步骤6将待测老年人热舒适预测样本输入到训练好的上述模型进行计算，得到老年人热舒适的预测结果。

3 案例研究

以杭州地区为例，进行老年人热舒适仿真研究。杭州属于典型的夏热冬冷地区，且人口老龄化趋势十分显著，据杭州统计局数据[12]，杭州市60 岁及以上老年人口占人口总数的比例从2010年的17.13%逐年增加至2018年的22.53%。杭州地区人口老龄化的趋势与全国老龄化趋势是基本一致的。以杭州地区为例进行老年人热舒适研究，可为夏热冬冷地区的其他城市提供较大的参考。

3.1 确定影响因素

老年人热舒适受众多因素的影响，按照老年人背景信息、行为习惯、居住建筑信息及热环境物理参数4 个类别，选择17 个因素作为老年人热舒适影响因素，如表1所示。

表1 老年人热舒适预测影响因素

3.2 数据收集与预处理

基于确定的老年人热舒适影响因素，通过测试、问卷调查以及访谈方法，建立杭州地区老年人热舒适仿真数据库，所构建的数据库包括844 个样本。

3.2.1 数据收集对象

选择杭州地区8 所养老机构进行调研，共对844 名老年人进行访谈和问卷调查。所调查养老机构位置含盖市区和郊区，主办单位包括政府和个人。所调查的老年人均思维清晰，能进行正常交流。被调查老年人的年龄范围如表2所示，平均年龄84.34 岁，其中男性315 人，女性529 人。

表2 老年人年龄范围

3.2.2 环境参数测量

采用CENTER310数字式温湿度仪和KANOMAX KA23热线式风速仪对老年人居住环境进行测试，测试参数包括：室内外空气温度、室内外相对湿度、室内外风速。测试方法参照文献[13-14]的相关规定。室内测试点选取在受访者腹部周围，对于静坐者测量高度距离地面0.6 m左右，对于站立者测量高度距离地面1.1 m左右。室外测位点于被调研建筑附近空旷的场所，距离地面高度1.5 m处，且避免太阳直射。测量时老年人居室状态与测量前一致，保持门、窗等的最初状态。

3.2.3 问卷调查及访谈

通过问卷调查、访谈以及现场观察等方式，收集包括老年人背景(性别、年龄、健康状况和在当地的居住时间等)、老年人居住建筑(建筑朝向、居住楼层和居住户型等)以及老年人的行为习惯(当时的着装、活动状态、开窗状态和窗帘状态等)等信息。采用标准7 级热舒适标尺(-3冷，-2凉，-1稍凉，0适中，1稍暖，2暖，3热)确定老年人的主观热舒适评价。调研人员现场向老年人解释问卷内容，并以访谈形式协助不便于填写问卷的老年人完成调研。

3.2.4 数据预处理

通过赋值将收集到的定性数据转化为离散数据描述。如将性别女、男分别赋值为1和2，健康状况(自助、介助、介护)赋值为1，2，3，着装情况转化为服装热阻，活动状态转化为代谢率。根据文献[13-14]的相关规定，按照单件服装热阻求和的方式确定受试者全套服装热阻[15]。在老年人单件服装热阻的基础上，运用Cullough等[16]提出的计算式对服装热阻进行修正，表达式为

Icl=0.676×∑Ichl+0.117

(10)

式中：Icl为全套服装热阻；Ichl为单件服装热阻。

3.3 确定C4.5算法和CART算法权重β1和β2

基于杭州地区老年人热舒适仿真数据库，执行步骤2～4，采用C4.5算法和CART算法构建老年人热舒适决策树模型，并进行老年人热舒适预测，得到C4.5算法和CART算法的预测准确率分别为57.14%和73.81%，进而得到C4.5算法和CART算法对应的权重分别为β1=0.4，β2=0.6。模型构建和相关计算在Matlab平台上编码完成。

3.4 基于混合分裂算法决策树构建杭州地区老年人热舒适仿真随机森林模型

在Matlab平台上编码实现基于混合分裂算法决策树构建杭州地区老年人热舒适仿真随机森林模型，将数据库中80%的数据作为训练数据集进行模型训练，影响因素数据作为模型的输入，老年人热舒适等级作为输出，通过执行步骤5，构建完成老年人热舒适随机森林模型。训练数据集之外的数据作为验证数据集。

随机森林算法有两个影响其性能的重要参数，分别为随机森林中决策树的棵数P以及决策树的节点分裂随机变量U。随机森林决策树的棵数对于随机森林算法的效率有着重要的影响，P值越大，模型越复杂度，随机森林算法的运行效率会下降；P值过小，随机森林算法的分类精度可能下降或者出现过拟合现象[17]。在杭州市老年人热舒适仿真中，决策树棵数P与袋外数据误差率的关系如图1所示。由图1可知：决策树大于一定数量后，袋外数据误差率呈现出稳定趋势并且处于较低值，兼顾模型复杂性，本模型确定250为最优决策树棵数。

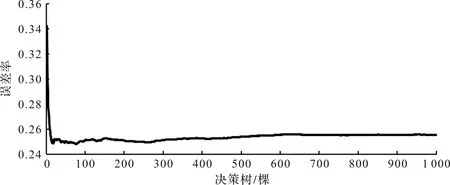
图1 决策树棵数与袋外数据误差率的关系

Breiman[10]通过实验验证在节点分裂随机变量U值较小时，U值取log2M+1较合适，其中M是数据集中特征变量个数。曹正凤[18]发现随机特征变量U值达到一定程度后，对算法的影响不明显，但随着U值的增加会使得决策树的运行效率下降，因此需要根据实际情况选择最佳的U值。在杭州市老年人热舒适仿真中，节点分裂随机变量与袋外误差率的关系如图2所示。由图2可知：当U=7时，出现袋外数据误差率明显下降，且之后逐渐降低，故本模型确定7为最优节点分裂随机变量值。

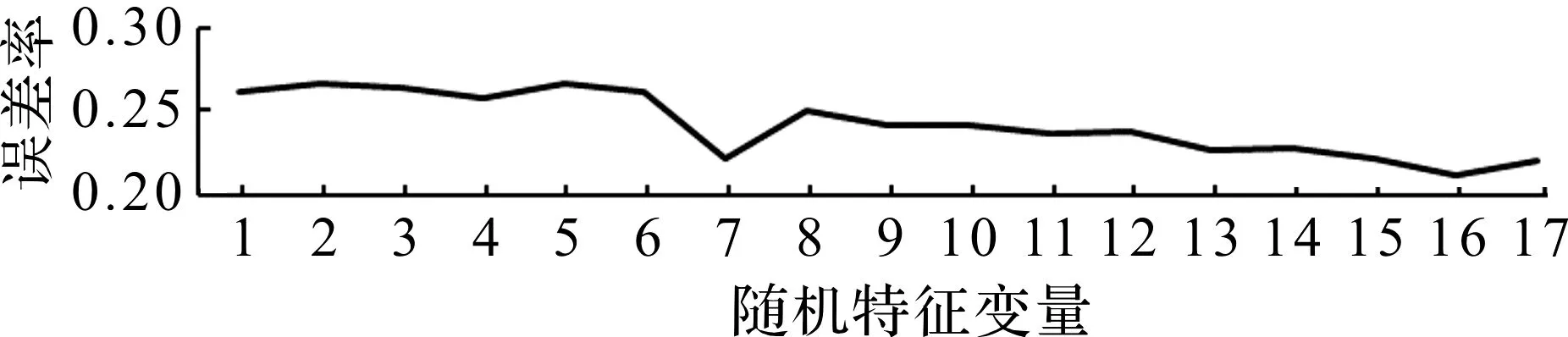
图2 节点分裂随机特征变量与袋外误差率的关系

3.5 模型验证

将验证数据集输入到训练好的老年人热舒适随机森林模型中，预测结果如表3所示。由表3可知：预测准确率达到82.25%，远高于文献[8]中传统PMV模型51%的预测准确率。

表3 基于验证数据集的预测结果

3.6 老年人热舒适影响因素权重

基于本模型对杭州地区老年人热舒适仿真过程，17 个影响因素量化权重如图3所示。由图3可知：老年人热舒适影响因素的重要程度依次为服装热阻、室内温度、室内湿度、室外湿度、室外温度、室外风速和年龄等，其中服装热阻、室内温度和室内湿度对老年人热舒适的影响较大。

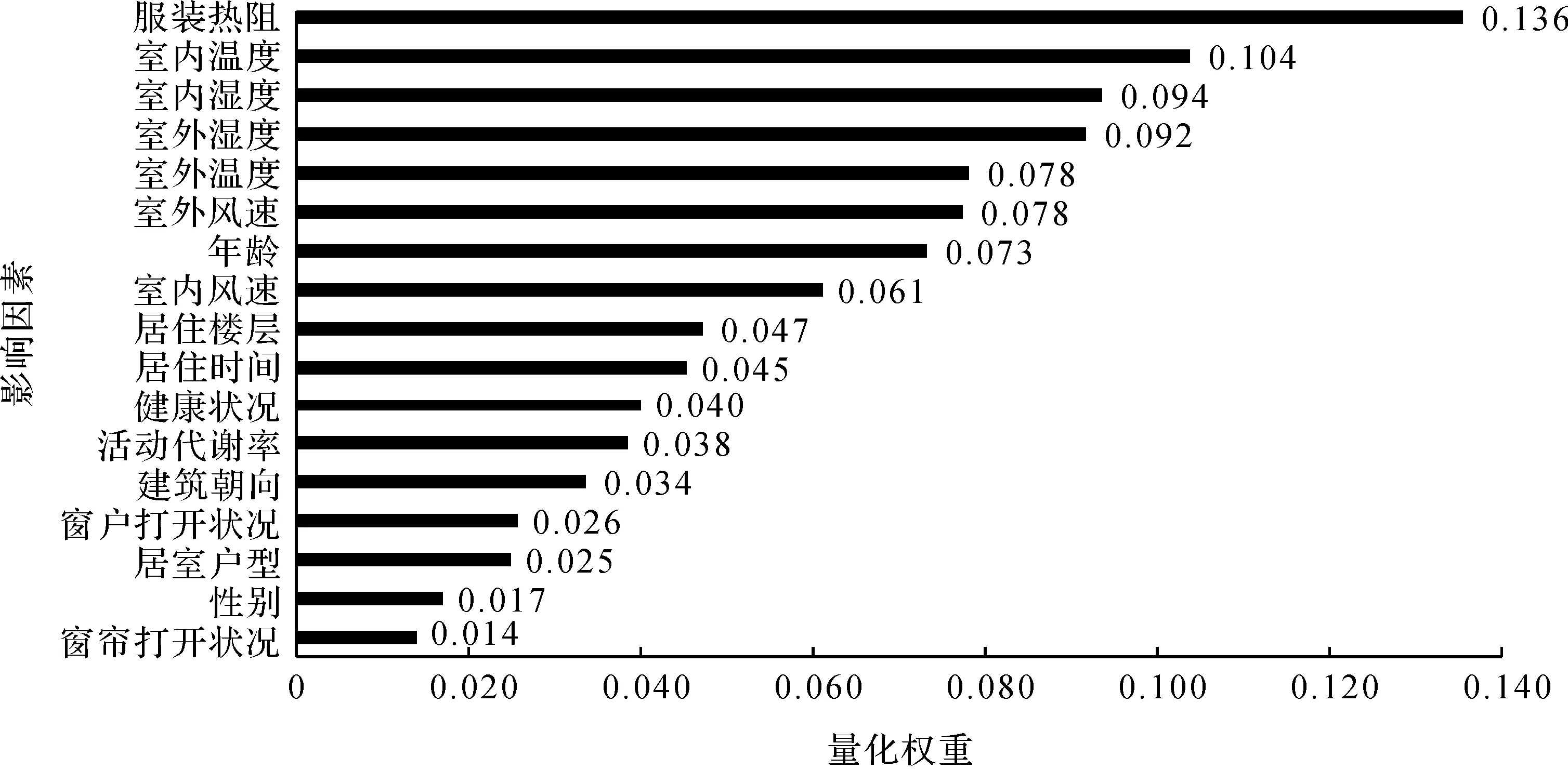
图3 老年人热舒适影响因素量化权重

4 模型性能讨论

基于杭州市老年人热舒适仿真数据库，将笔者提出的基于改进随机森林的老年人热舒适仿真模型与其他3 种模型性能进行比较，各种模型的性能参数如表4所示。

表4中MAE是一个平均偏差指标，RMSE是预测过程的另一常用指标，其计算式分别为

(11)

(12)

较低的MAE值意味着更好的预测性能，同样，较低的RMSE值表示仿真性能越好[19]。PMV模型预测方法采用我国《民用建筑室内热湿环境评价标准》[13]提供的计算程序，通过Matlab进行程序编译实现其仿真过程。几种模型的预测性能比较如表4所示。由表4可知：改进随机森林的老年人热舒适预测模型具有最高的预测精度，最低的预测误差。在建模工作量方面，改进随机森林的老年人热舒适预测模型需要最大的工作量，由于PMV为已有的热舒适预测模型，所以PMV没有建模工作量。

5 结 论

老年人心理和生理都有其特殊性，不宜直接采用传统的热舒适预测PMV模型进行评价。通过研究，提出了一种基于改进随机森林的老年人热舒适仿真理论模型。以杭州地区为例，确定17 个老年人热舒适影响因素，通过现场测试、问卷调查和访谈等方式构建老年人热舒适仿真数据库。以所构建的数据库为基础，对笔者提出的老年人热舒适仿真理论模型进行训练，得到C4.5和CART节点分裂算法的权重分别为0.4和0.6，以此构建混合决策树节点分裂算法，确定最优决策树为250 棵，最优节点分裂随机变量为7。通过验证数据集的验证，笔者提出的模型预测准确率达到82.25%。模型性能对比显示：改进随机森林老年人仿真模型在预测准确率、平均绝对误差和均方根误差等方面均优于传统随机森林、决策树算法以及PMV模型。基于仿真过程，为17 个老年人热舒适影响因素确定量化权重，权重分配表明服装热阻、室内温度和室内湿度对老年人热舒适影响最大。