如何正确运用Z检验——两总体率比较等效性Z检验及SAS实现

2021-01-23胡纯严胡良平

四川精神卫生 2020年6期

胡纯严，胡良平，2*

（1.军事科学院研究生院，北京 100850；

2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

在对临床资料进行统计分析时，研究者常选择的统计分析方法是差异性检验。其中，一般差异性检验［1-3］仅考虑差异是否具有统计学意义，而3种特殊差异性检验，即非劣效性检验、等效性检验和优效性检验［4］除了考虑差异应具有统计学意义外，还需要考虑应具有“临床意义”。本文将结合临床实际，介绍与“两总体率比较的等效性检验”有关的内容。

1 两总体率比较等效性Z检验的基本原理和方法

1.1 基本概念

等效性检验是指主要研究目的为显示两种治疗效果之间的差别大小在临床上并无重要意义的试验。在试验设计阶段需要设定等效性界值（δL，δU）来界定两种药物或两种治疗方案的等效性［4-5］。

1.2 问题与数据结构

【例1】一个新的抗肿瘤药物A与临床有效药物B对照进行临床试验，选取300例符合要求的患者并随机均分成两组，分别接受A药和B药治疗。试验结果为A药的有效率是58.00%（有效例数n=87），B药的有效率是46.00%（有效例数n=69）。现根据临床实际，设置等效性界限为10%，试问两种药物是否等效［6］？临床资料见表1。

表1 两组患者的治疗效果

【对数据结构的分析】该资料的试验因素为“药物种类”，其两个水平分别为“药物A”与“药物B”，观测指标为“有效率”，所以该资料为成组设计一元定性资料。

【统计分析方法的选择】研究者的研究目的是评价两种药物抗肿瘤效果是否等效，并且设定了等效性界值δL=-10%、δU=10%，这时应选用等效性检验。

【例2】在伊曲康唑治疗手足癣的平行对照临床试验中，335例患者入选，166例患者服用伊曲康唑400 mg/d，服药1周（治愈92例），169例患者服用伊曲康唑100 mg/d，连续服药4周（治愈98例）。设定等效性界值为12%，试问两种治疗方案是否等效？临床资料见表2。

表2 两组患者的真菌感染治愈率

1.3 基本原理

1.3.1 检验假设

规定整个等效性检验的检验水准α（每个单侧检验的检验水准为α'=α/2）的值。

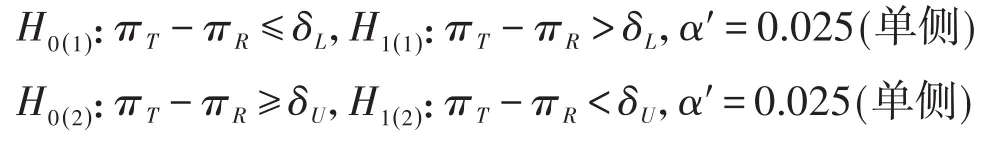
1.3.2 检验统计量

在式（1）和式（2）中，检验统计量Z服从标准正态分布；（PT、nT）与（PR、nR）分别为试验组（T）与对照组（R）的“样本率、样本含量”；δL与δU分别为等效性界值的下限（下限取负值）与上限。

1.3.3 基于检验统计量Z的取值计算单侧尾端概率

根据检验水准查表或借助相应的SAS函数进行计算，获得检验统计量Z的临界值（针对手工计算而言）和（或）标准正态分布尾端的概率（针对统计软件而言）。

1.3.4 得出统计学结论和专业结论

根据拒绝还是不能拒绝H0的结果，得出统计学结论，最后结合专业知识得出专业结论。需注意，须同时拒绝H0(1)和H0(2)，方能得出等效性结论。

2 两总体率比较等效性检验的SAS实现

2.1 基于SAS语言按公式编程间接实现计算

基于SAS语言和标准正态分布函数等知识［7］并按式（1）和式（2）进行编程，就可间接实现两总体率比较等效性Z检验。

由于典型的太行山地质构造，受储水层含水量的限制，和顺县境内泉水出漏量较小，联村集中供水工程不易采用泉水作为供水水源，而单村供水水源采用较多。主要优点：（1）当地的水资源达到充分利用，有效控制了地下水的开采量，使所属区域的地下水得到充分涵养。（2）山泉水水质优良是很好的饮用水水源。（3）水源建设形式简单，投资费用较小，多数山泉水所处地形较高属于高地泉，水借重力流向高位水塔，后期运行费用低。

SAS程序如下：

【程序说明】变量名后面的“_t”与“_r”分别代表“试验组”与“对照组”相应的量（包括样本含量与有效率）。等效性下界值应采用负值来表示。

【SAS输出结果】

【统计学结论】因Z1=3.841，P=0.000061（单侧概率）＜0.025，所以，应拒绝H0(1)，接受H1(1)，又因Z2=0.349，P=0.63654（单侧概率）＞0.025，所以，应接受H0(2)。

【专业结论】在等效界值为（-0.10，0.10）的前提条件下，药物A与药物B不等效。

2.2 基于SAS中FREQ过程直接实现计算

由于SAS中FREQ过程包含了几乎绝大多数定性资料假设检验方法［8］，所以，此处将采用此过程来直接实现两总体率比较等效性Z检验。

SAS程序如下：

【程序说明】各组中的数据应为“有效例数”与“无效例数”，而不适合直接采用“有效率”。程序中equiv表示进行等效性检验，MARGIN=0.10表示等效界值（即下界值为-0.10、上界值为0.10），若下界值与上界值的绝对值不相等，需要明确写出，例如：MARGIN=（-0.12，0.15）（注意：下界值必须采用负数）。

第1部分输出结果：

第2部分输出结果：

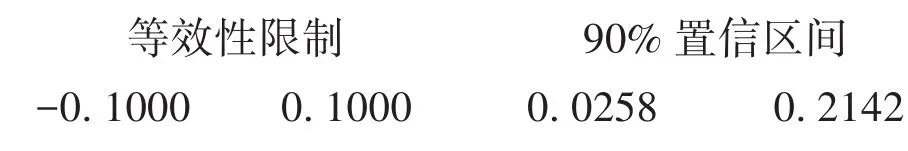
【统计学结论】由第1部分输出结果可知：因Z1=3.8414，P＜0.0001（单侧概率）＜0.025，所以，应拒绝H0(1)，接受H1(1)。又因Z2=0.3492，P=0.6365（单侧概率）＞0.025，所以，应接受H0(2)。由第2部分输出结果可知：两总体率之差的90%置信区间为［0.0258，0.2142］，该区间包含了等效性上界值δU=0.10，说明与上界值对应的等效性检验未通过，即不等效。

【专业结论】在等效界值为（-0.10，0.10）的前提条件下，药物A与药物B不等效。

3 讨论与小结

3.1 影响等效性检验结果的因素

等效性检验结果不是绝对的，随着条件的改变，最终的检验结果也会发生相应的改变。具体地说，影响其结果的因素有“显著性水平α”“等效性界值（δL，δU）”和“样本含量”。

3.1.1 α的取值对等效性检验结果的影响

等效性检验结果与显著性水平α有密切关系。现以例2的数据为例，若取每个单侧检验的显著性水平α=0.025，等效界值取为（-0.12，0.12），计算结果为Z1=1.7428，P=0.0407＞α=0.025；Z2=-2.6911，P=0.0037＜α=0.025，结论为两药不等效。若取每个单侧检验的显著性水平α=0.05，由前面的计算结果（两个P值都小于0.05）可知，结论为两药等效。

3.1.2 等效性界值(δL，δU)的取值对等效性检验结果的影响

等效性检验结果与等效性界值（δL，δU）的取值也有密切关系。现仍以例2的数据为例，若取每个单侧检验的显著性水平α=0.025，等效界值取为（-0.12，0.12），计算结果为Z1=1.7428，P=0.0407＞α=0.025；Z2=-2.6911，P=0.0037＜α=0.025，结论为两药不等效。若取每个单侧检验的显著性水平α=0.025，等效界值取为（-0.14，0.14），计算结果为Z1=2.1123，P=0.0173＜α=0.025；Z2=-3.0606，P=0.0011＜α=0.025，结论为两药等效。

3.1.3 样本含量对等效性检验结果的影响

若保持“3.1.3”中“两药不等效”情况的大部分条件不变，仅改变样本含量，例如，两组样本含量都扩大10倍，即A药组有效例数为920例，无效例数为740例；B药组有效例数为980例，无效例数为710例。计算结果为Z1=5.5113，P＜0.0001；Z2=-8.5100，P＜0.0001，结论就变为“两药等效”。即使样本含量扩大2倍，也能得出“两药等效”的结论。需注意的是，在拟开展等效性试验研究之初期，就应当按照已知的条件［包括两组估计的有效率、显著性水平α的值、检验效能（1-β）的值和等效性界值（δL，δU）的值］，找到相应的计算公式，估计出合适的样本含量［4］。