基于改进A*算法室内移动机器人路径规划
2021-01-22刘子豪赖坤城王玺乔
刘子豪,赵 津,刘 畅,赖坤城,王玺乔
贵州大学 机械工程学院,贵阳550025
在机器人领域中,路径规划一直是国内外研究的热点话题。路径规划是指移动机器人在通过传感器获得所处环境的全局信息之后,通过路径规划算法来规划出一条最优路径,可以使得移动机器人安全且快速地由起始点运动到目标点[1]。
A*算法作为一种智能启发式算法,由于自身的可移植性和可塑性较强,应用领域广泛[2],例如航空航天[3]、农业[4]、制造业[5]、仓储物流[6-7]等。但传统A*算法有着先天的不足之处。在前期进行路径点搜索时,需要维护Openlist 和Closedlist 两个列表。在进行子节点计算时,需将父节点周边八个点全部加入到Openlist 进行计算,寻找启发代价最小的点作为下一个父节点,迭代运行[8]。因此当环境信息复杂,场景比较大时,许多不必要的节点都会被计算,造成了内存开销过大、寻路时间变长的问题;在由父节点搜寻下一个子节点的过程中,子节点只能在父节点周边八个相邻的节点中产生,因此,父节点与子节点之间存在着π/4的角度限制[9],会造成一些不必要的转折,使得路径变长;传统A*算法中,没有对路径进行平滑处理,因此,规划好的路径的转折比较剧烈,不利于移动机器人的路径跟踪。针对上述问题,国内外研究人员提出了一些改进方法。例如,文献[10-11]提高了运算速度,文献[12]提高了路径的平滑程度,文献[13]提高了转弯的曲折程度,但没有对上述三个问题一起改进的研究成果。
因此针对传统A*算法在寻路过程中所需时间过长、路径转折多以及所规划的路径不平滑的问题,本文首先结合跳跃点搜索理论,剔除传统A*算法中所不需要计算的节点,减小了计算量,提高了运算速度,其次对所得到的路径进行二次规划,删除不必要的转折点,降低路径长度。接着将二次规划得到的路径,在拐点处进行优化处理,使所得到的路径更加平滑。最后,将本文提出的算法应用于Turtlebot3 移动机器人中,在室内进行全局路径规划实验,实验结果表明,本文提出的算法在运行时间、路径长度、平滑程度上相比于传统的A*算法都有很大的提高。
1 传统A*算法
机器人进行路径规划前,需建立自身所用地图,根据地图种类可分为栅格、拓扑地图等,栅格地图由于自身模型简单且对环境有很好的表达,在路径规划时被广泛采用,因此本文将采用栅格法来构建地图。栅格地图是将机器人得到的2D环境信息地图进行相同尺寸的栅格划分。根据栅格中是否有障碍物将栅格分为白色可通行栅格和黑色不可通过栅格。
栅格地图中路径规划实例如图1所示,周边环境固定,绿色的点为起点,红色的点为终点,黄色的线为规划的路径。

图1 规划路径
A*算法是一种在静态环境下获得最优路径的启发式算法。该算法通过计算估价函数,来确定接下来的搜寻和运动方向。首先,起点必须放入Openlist列表,将起点作为父节点,放入Closelist列表,向周边扩展计算,得到周边八个节点的代价值,选择最小的节点作为下一个父节点,再以此节点向周边进行扩展计算,得到代价值最小的节点作为下一个父节点,依次迭代,直到终点。由于在路径搜寻的过程中,每一个节点的代价值均是最小。因此,得到的路径一定为代价最小的最优路径。A*算法估价函数为:

Fn表示起始点到任意节点的估价值,Gn表示起始点到某一个节点的实际代价,Hn表示起始该点到终点的估计代价值。本文采用欧式距离作为启发式函数:

起始点横坐标为xi,起始点纵坐标yi。终点横坐标xn,终点纵坐标yn。
图2为A*算法的实例。

图2 传统A*算法寻路
由上述传统A*算法步骤可知,在运行过程中,需要对Openlist和Closelist两个列表进行维护。图2中,绿色为选出的路径点,粉色区域为A*算法需要计算的点,黑色的线条为规划好的路径。由图2得出,粉色的区域为A*在寻路过程中需要计算的节点,但大部分节点都与生成的路径无关,造成传统的A*算法在大范围寻路过程中存在计算量过大、内存消耗严重的问题。在规划好的路径中存在着不必要的转折点,例如点S 可以直接到点C。并且,传统A*算法规划好的路径转折剧烈,不利于机器人进行路径跟踪。
2 改进A*算法
本文针对传统A*算法计算量大、转折点过多、路径不平滑的问题,提出了一种改进算法。首先基于关键点选取的策略来代替传统A*算法中的Openlist和Closelist两个列表,之后将得到的路径进行二次规划,删除冗余点,最后对转折处进行路径平滑处理,得到一条最优路径。
2.1 关键点选取
本文受跳跃点算法的启发,提出了一种关键点搜索的策略。如图3 所示,起始点为S,终点为G 。关键点搜索策略的本质就是给A*寻路算法一个先验信息,利用选取所得到的关键点来代替传统A*中Openlist 的点进行计算,如本例中,S 为起点,G 为终点。按照传统的A*算法,应首先计算(1,2),(2,1),(2,2)这三个点的代价值,选择(2,2)点作为下一个父节点,并计算其周边的八个点的代价值,再选择代价最小的路径,即图3 中所有的点都需要进行计算。但在图中,可以明显得出,S →(2,2)→G 为一条最优路径,与之无关的点均不需要计算。在下文提出了具体策略,使得在寻路过程中,路径仅仅经过(2,2)点。这样就解决了传统A*算法在寻路上存在的内存开销过大的问题。在文献[14]中提出了一种策略,本文基于此,做出了调整,提出了自己的关键点策略。通过对A*算法和实际路径规划情况分析,可知,当路径点周边存在障碍物和不存在障碍物时搜寻路径的关键点不同,因此提出了下列两种情况关键点的选取策略。

图3 关键点
2.1.1 两点共线,且周边不存在障碍物
在图4 中J 和G 是A*算法中的任意节点,J 为父节点。根据图可以得出,在J 到达G 时,一共存在着两类路径。一种是直线路径,由J 经由x 直接到G 点。另一种为折线路径,不经过x,由J 折线到达G 点。对比在这两种情况中,沿直线运动的方式花费的时间最短。在传统的A*算法中,途中所有的栅格点都需要进行计算,但图中的灰色部分计算无意义。因此为了删减这些不必要的点,采用下面策略:

jx 与jg 均为向量。因此,当共线时,仅选取该线段的端点,比如图中的G 点,作为关键点。

图4 选取关键点
2.1.2 两点不共线,但周边存在障碍物
在进行A*算法时,需要越过障碍物进行寻路,如图5 所示,因此当周边存在障碍物时,上述所给出的策略就需要做出相应的调整,提出了强制关键点策略:

jx、jf、jn、nf 均为向量。n 为除x 点外任意一点。当F 点满足上述关系式时,将其定义为强制关键点,在进行路径规划时,这些强制关键点必须进行计算。

图5 强制关键点
在应用改进的A*进行路径规划时,由起始点开始检测,先搜寻水平方向,当水平方向上有障碍物或者碰触到边界,且不能搜寻到强制关键点时,搜寻停止,改为搜寻对角线方向,当对角线到一个新节点时,按照之前的策略再进行搜寻,寻找到关键点后,将关键点作为下一个搜寻的起始点,进行搜寻,一直搜寻到终点为止。寻路过程如图6所示。

图6 关键点寻路实例
2.2 二次路径规划
在传统的A*算法中,路径只进行一次规划,得到一条在A*算法约束条件下的最优路径。由于自身在搜寻过程中只能向周边八个点进行扩展搜索,因此存在π/4的角度限制,使得路径中依然存在着冗余转折点。在这种情况下,进行二次路径规划,将得到的原始路径,进行冗余点删除的处理,使得路径长度变短。在二次路径规划时,本文提出了一种反向动态搜索的策略。将路径的终点作为二次路径规划的起始点,同理,路径的起始点作为二次规划搜寻的终点。由起始点向下一个顶点连接,假如没有遇到障碍物,迭代进行。直到遇到障碍物时,将其路径中心点相连,检查是否穿过障碍物,如果没有,连接两点,如果有障碍物,则连接中点与靠近终点端四分之一处。一直取原来的二分之一长度作为路径的搜寻点,直到两个路径的长度之间没有较大的变化为止(视地图尺寸为定,本文地图大小为7.5 m×7.5 m,经多次实验验证,选择长度比为0.9)。将最终得到的点连接,得到二次规划的路径。
2.3 路径平滑
在经过2.1和2.2节处理后,得到了一条基于本文搜索策略的最优的路径,但在图6 中可以看出,二次规划的路径转折十分剧烈,室内机器人在进行路径跟踪时,没有好的跟踪效果。因此,需要对得到的路径进行平滑处理。Hybird A*算法[15]对路径平滑有很好的处理效果,但时间花费高,计算开销大,并且容易陷入局部最优。在本文中,提出了一种动态相切圆策略。在2.2 节的基础上,选取与障碍物不相交的拐点和路径与障碍物的交点作为优化点。对比优化点两侧的路径,选取小的路径的二分之一长度,分别做垂直,选取两条垂线的交点作为圆心,画一条圆弧来代替原来的转折点,达到路径平滑的作用。实验可以得知,虽然平滑效果不如Hybird A*,但运算效率高,并且完全可满足室内移动机器人的路径跟踪。
3 实验
3.1 仿真实验
经本文算法得出的路径与传统A*算法的路径如图7所示。
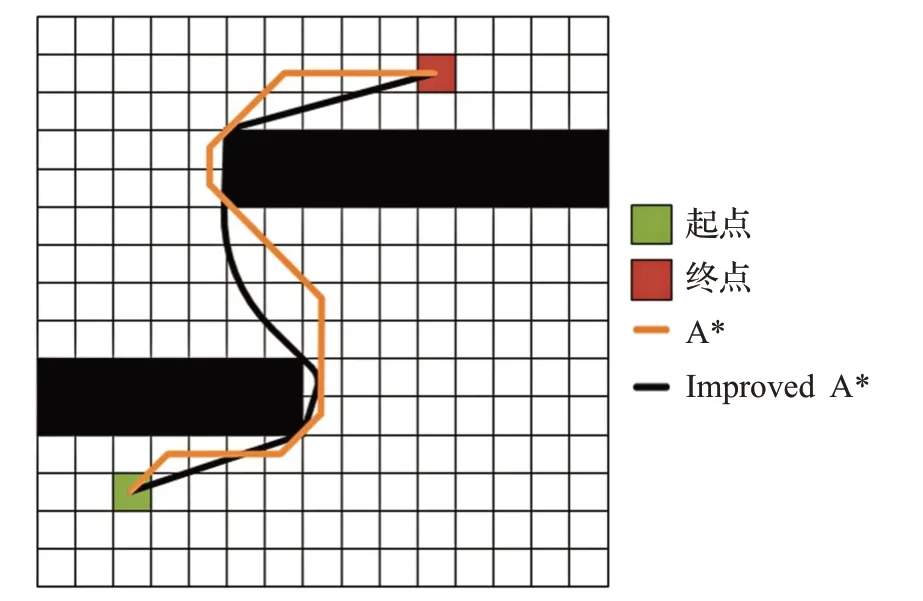
图7 A*与Improved A*
由图7可以看出,本文提出的改进算法在路径长度和弯折角度较传统A*算法有着明显的提高,在运算时,传统A*算法所需的时间为3.02 ms,改进的A*算法为0.994 ms,运算效率提高了67%;传统A*算法路径长度为301.5 cm,本文算法为293.4 cm,减小了2.7%。为了验证该算法的通用性,再选取栅格边长为10 cm,地图大小分别为15×15、30×30、50×50 的环境中进行仿真实验。实验选择固定起点与终点,随机环境进行实验,每一组地图均进行15组随机实验。时间单位为1×10-6s,路径单位为厘米。实验结果如图8、9所示。
通过45 组仿真实验数据可以得出,本文提出的算法在时间上平均为A*算法运算时间的56.09%,路径长度降低为原来的97.94%。并且,根据地图大小和障碍物数量的不同,可以得出本文所提出的算法,在大尺寸、多障碍物的环境下,运算速度、路径长度明显优于传统A*算法。
3.2 真实环境实验

图8 三种环境时间

图9 三种环境路径长度
实验所采用的机器人为Turtlebot3buger。该机器人搭载Raspberry Pi 3树莓派3开发板、OpenCR底层控制器,重量为0.995 kg,大小为138 mm×178 mm×192 mm。机器人运动时通过OpenCR 主板控制底部的两个带编码器的减速电机,进行速度控制,使其转弯或者直行。机器人如图10所示。

图10 Turtlebot3buger
实验环境如下,采用边长15 cm、大小为12×12的栅格模型进行建图,得到的栅格环境地图及规划好的路径如图11所示。设定起点坐标为(2,2),终点坐标为(7,11)。将规划好的路径移植到机器人的开发板中,使机器人自主进行路径跟踪。实验效果表明,在运算速度,路径长度、平滑程度上,较传统A*算法均有明显提高,如表1所示。
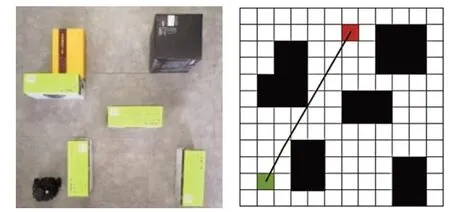
图11 实验环境(左)栅格地图路径规划结果(右)

表1 A*与Improved A*对比
4 结论
本文以提出的关键点策略、二次路径规划以及路径平滑策略,对传统A*算法进行改进。关键点策略减小了传统A*算法中的内存消耗,提高了机器人的寻路效率。二次路径规划及路径平滑降低了传统A*算法的路径长度以及转折角度,使机器人在路径跟踪时效率和跟踪效果提高。并且,本文提出的算法在场景大且环境较为复杂时,提升的效果尤为显著。将本文算法应用于turtlebot3buger机器人中,实验结果表明,改进的A*算法较传统A*算法优势明显。
