基于弹簧回综的消极式凸轮开口仿真设计*
2021-01-22邱海飞
邱海飞,党 波
(西京学院 机械工程学院,陕西 西安 710123)
0 引 言
在织造生产过程中,开口机构通过综框将上下层经纱迅速分离形成梭口,综框运动规律和机织物结构均受开口形式影响[1]。按照对织物组织的适应能力,一般可将开口机构分为连杆、凸轮、多臂和提花4大类。凸轮开口机构主要适用于现代高速织机相,对于其他3类开口形式,凸轮开口具有结构简单、运动平稳、振动冲击小等特点,目前已被广泛应用于高速喷气织机和喷水织机。
国内关于凸轮开口的技术探索和科学研究,主要集中在动力学计算、反求设计和回综分析等方面,如葛正浩等[2]通过凸轮测绘、CREO建模及动态仿真,实现了共轭凸轮开口机构的反求设计和动力学分析;魏展等[3]通过建立消极式凸轮开口机构动力学模型,推导出了光滑无冲击的凸轮轮廓线设计方程,验证了高速凸轮运转时的动力学特性;崔鸿钧[4]对凸轮开口的回综弹簧进行了理论分析和设计计算,并深入分析了弹簧初伸长的影响因素。国外方面,KISALAY D等对凸轮开口机构的摆线设计进行了深入研究;EREN R等研究了凸轮开口机构的设计方法;KARANHAN M等[5]对基于凸轮开口的综框运动规律进行了分析和比较研究。一些国际知名织机生产厂商,如瑞士苏尔寿、德国多尼尔、比利时必佳乐、意大利舒美特等生产的喷气织机一般都采用凸轮开口,而且在织机综合性能方面已达到较高水平。
本文设计一种由凸轮、齿轮、连杆及拉压弹簧构成的消极式开口机构,不同于以往采用钢丝绳和滑轮进行传力提综的消极凸轮开口,这种直吊式弹簧回综凸轮开口具有结构紧凑、承载力强、回综迅速、传力均匀等特点,避免由于钢丝绳与滑轮摩擦所造成的机修及维护,有利于提高消极式凸轮开口的机件寿命和运行效率,具有良好的综合工作性能及应用前景。
1 凸轮开口原理
根据回综方式不同,可将凸轮开口机构分为积极式和消极式。积极式开口采用共轭凸轮来实现综框的升降运动,多适用于宽幅中、低速重载织物[6];而消极式开口则是在凸轮驱动的基础上,通过弹簧来完成综框的升程或回程,主要适用于高速轻载织物。
根据消极式开口织造工艺,本文设计了一种直吊式弹簧回综凸轮开口机构,如图1所示。
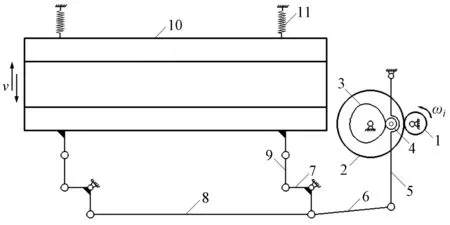
图1 消极式凸轮开口机构简图
其工作原理为:在电动机逆时针驱动下,小齿轮1将扭矩和转速传递至大齿轮2,然后大齿轮2同轴带动凸轮3作顺时针运转,并使滚子4和摆杆5沿固定铰支点发生往复摆动,同时通过推杆6将动力传递至二臂杆7和横杆8,最后由拉杆9带动综框10下降至最低点(梭口满开),此为凸轮提综过程(推程)。随着凸轮3的顺时针运转,滚子4经远休状态后进入回程阶段,此时由回综弹簧11拉动综框10向上运动至最高点(梭口满开),此为弹簧回综过程。紧接着,综框在短暂静止后(近休)随凸轮运转进入下一次开口循环。
通过机构学分析可知,去除虚约束和局部自由度之后,该机构共包括7个活动构件、9个低副和2个高副,代入下式:
F=3n-2PL-PH
(1)
式中:F—平面机构自由度数目;n—活动构件数目;PL—低副数目;PH—高副数目。
计算得出凸轮开口机构自由度等于1,符合机构学设计要求。
2 凸轮理论廓线
考虑到凸轮开口机构高速、轻载的性能特点,本文采用无冲击正弦加速曲线作为摆动滚子从动件运动规律,在此基础上通过反转法构建凸轮廓线方程。当基圆半径为50 mm时,凸轮理论轮廓线设计方程如下式所示:
x=asinθ-lsin(φ+φ0+θ)
(2)
y=acosθ-lcos(φ+φ0+θ)
(3)
式中:x,y—滚子中心点坐标;a—连心线长度,mm;l—摆杆长度,mm;θ—凸轮轴转角,rad;φ—摆杆摆角,rad;φ0—摆杆与连心线夹角,rad[7]。
凸轮的实际轮廓线是理论轮廓线的等距曲线,其距离等于滚子半径rr。
为了与综框升降运动相匹配,令推程运动角δ0等于回程运动角δ0′(即120°),远休止角δ1等于近休止角δ2(即60°)。凸轮转动一周,摆动滚子从动件依次经历推程—远休—回程—近休4个阶段,与此同时,综框完成一次升降运动。随着凸轮机构的持续运转,综框按照这一运动规律作周期性开口运动。
3 理论设计与样机
3.1 力学模型
在凸轮提综运动过程中,综框是主要的承载部件,除了回综弹簧的弹性力以外,经纱张力、凸轮机构转化力、机械干摩擦力等均会直接或间接作用于综框。
凸轮开口机构力学模型如图2所示。

图2 开口机构力学模型
根据动力学理论建立综框运动微分方程,如下式所示:
(4)
式中:M—开口机构转化质量,kg;C—粘性阻尼系数,N·s·mm-1;K1—回综弹簧刚度系数,N/mm;G—开口机构转化重量,kg;N—凸轮对综框的转化作用力,N;F—干摩擦力,N;T—动态经纱张力在垂直方向的合力,N;X—综框位移,mm;X0—回综弹簧初伸长,mm。
上式中,当综框位于经直线以上时,经纱张力T取+号;反之,经线张力T取-号。令纱线刚度系数为K2。凸轮提综时,干摩擦力F取-号;弹簧回综时,干摩擦力F取+号[8]。
3.2 回综弹簧刚度
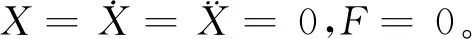
要使滚子与凸轮在任意时刻保持接触,必须使凸轮对综框的转化作用力N>0。
回综弹簧初张力K1X0应大于开口机构转化重量G与最大经纱张力T1max之和:
K1X0>G+T1max
(5)
式中:T1max—经纱张力最大值,N。
为了减小凸轮开口机构受力,应尽量使K1值较小,然而由于机械结构和空间位置限制,K1值实际上取决于弹簧初伸长X0,设计回综弹簧刚度时应先设定X0值,然后计算出K1的最小值,即:
(6)
式中:K1min—回综弹簧刚度系数最小值,N。
当综框位于梭口满开上限和下限位置时,单根纱线在垂直方向上的合力最大,分别为T1max=0.06 N和T2max=0.04 N[9]。以幅宽d=190 cm的纯棉织物为织造对象,查阅棉纺织手册可知,粗平布纯棉织物经密ρf=218.5根/10 cm。将各参数代入下式:
(7)
式中:Tpmax—片纱张力最大值,N;d—织物幅宽,cm;ρf—织物经密,根/10 cm;Tmax—单根纱线垂直方向最大张力,N。
由此便可计算出梭口满开时上、下层片纱张力最大值,即:T1pmax=124.55 N,T2pmax=83.03 N。
综框选用质量轻、强度高的铝合金,其余传动零部件均采用钢质材料,在ADAMS中测算得出开口机构转化重量G约为369.55 N。令弹簧初伸长X0=8 cm,将G值和T1pmax值代入式(6)即可计算出力学模型中的理论弹簧刚度K1=K1min=6 176.25 N/m,由此可知单根弹簧的理论刚度约为3 088.13 N/m。
为使弹簧具有足够的刚度储备,实际设计弹簧时将K1提高30%,则弹簧刚度K1增大至4 014.57 N/m(约4.01 N/mm),由虎克定律可知,此时弹簧初张力应为321.17 N。
3.3 功能型样机
根据凸轮廓线方程和机构学原理,本文利用第三方CAD软件设计盘形凸轮和相关构件几何模型,在此基础上装配形成能够驱动单页综框的凸轮开口机构组件,然后导入ADAMS/View环境下设置约束条件和相关参数,建立功能型仿真样机模型,如图3所示。

图3 凸轮开口机构仿真模型
图3中,综框运动和弹簧拉压沿Y方向,凸轮及齿轮转动绕Z轴方向,其余构件运动均在XY平面。
利用线性弹簧—阻尼元件模拟凸轮开口机构回综弹簧和系统阻尼,将其施加于综框上横梁两侧并与大地固接。
假设凸轮开口机构为小阻尼系统,令阻尼系数C=0.035。大小齿轮传动速比为1 ∶3。根据回综弹簧设计结果分别设置弹簧刚度、初伸长及初张力,并在凸轮和滚子之间施加实体接触。
4 仿真计算与分析
4.1 经纱张力模拟
综框升降运动使上、下层经纱往复交替形成梭口,这一过程经纱张力会随梭口大小而不断发生变化,即动态经纱张力。
利用Step函数模拟动态经纱张力变化,如下式所示:
y=step(t,t0,y0,t1,y1)
(8)
式中:t—自变量,s;y—函数值,N;t0—阶跃起点自变量值,s;y0—阶跃起点函数值,N;t1—阶跃终点自变量值,s;y1—阶跃终点函数值,N[10]。
其中,Step函数以时间t为自变量,通过三次多项式逼近任意时刻的纱线张力阶跃值。
小齿轮输入转速为1 800 r/min,则经大齿轮减速后凸轮轴转速为600 r/min,此即开口主轴转速。
根据综框运动规律,将上、下层片纱张力最大值(T1pmax、T2pmax)代入Step函数,构建动态纱线张力变化曲线,如图4所示。

图4 动态经纱张力模拟曲线
由图4可以清楚地看到:在0.1 s时间内,凸轮轴转动一周,综框完成一次升降运动,经纱张力也随之发生一次周期性变化。当综框运动至于上、下限位置时,梭口处于满开状态,对应动态经纱张力达到最大,并且张力值在综框短暂静止阶段(即远休、近休)也保持不变,符合经纱张力实际变化情况。
4.2 综框及凸轮运动规律
笔者设置仿真时间为0.3 s、仿真步长为1 500,在凸轮轴转速为600 r/min条件下,执行运动学仿真计算。
获得的综框运动学曲线如图5所示。
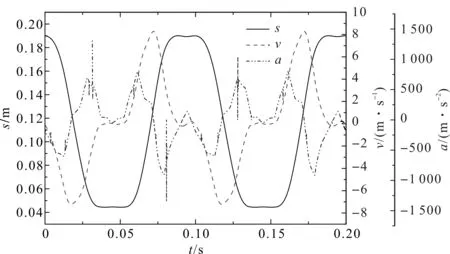
图5 综框运动学曲线
由图5分析可知:综框在0.1 s内完成一次升降运动,且位移曲线光滑、爬升平稳,综框行程约14.5 mm。当梭口满开时,综框速度接近于0且变化平缓(作短暂停留),有利于延长引纬时间;在综平位置时,综框速度达到最大,有利于快速分离上、下层经纱,开清梭口;在综框运动起始和终止处,加速度最小且无明显波动,有利于减小综框振动。可见,综框运动规律符合开口技术要求。
同样,可从ADAMS后处理模块获得其他关键构件的运动学曲线。
滚子从动件在X方向的线性运动规律如图6所示。

图6 滚子从动件运动学曲线
从滚子位移曲线可清楚看到:凸轮的推程—远休—回程—近休运动过程,且速度、加速度在远休和近休阶段均为0,说明凸轮与滚子之间无冲击。
摆杆角运动规律曲线如图7所示。
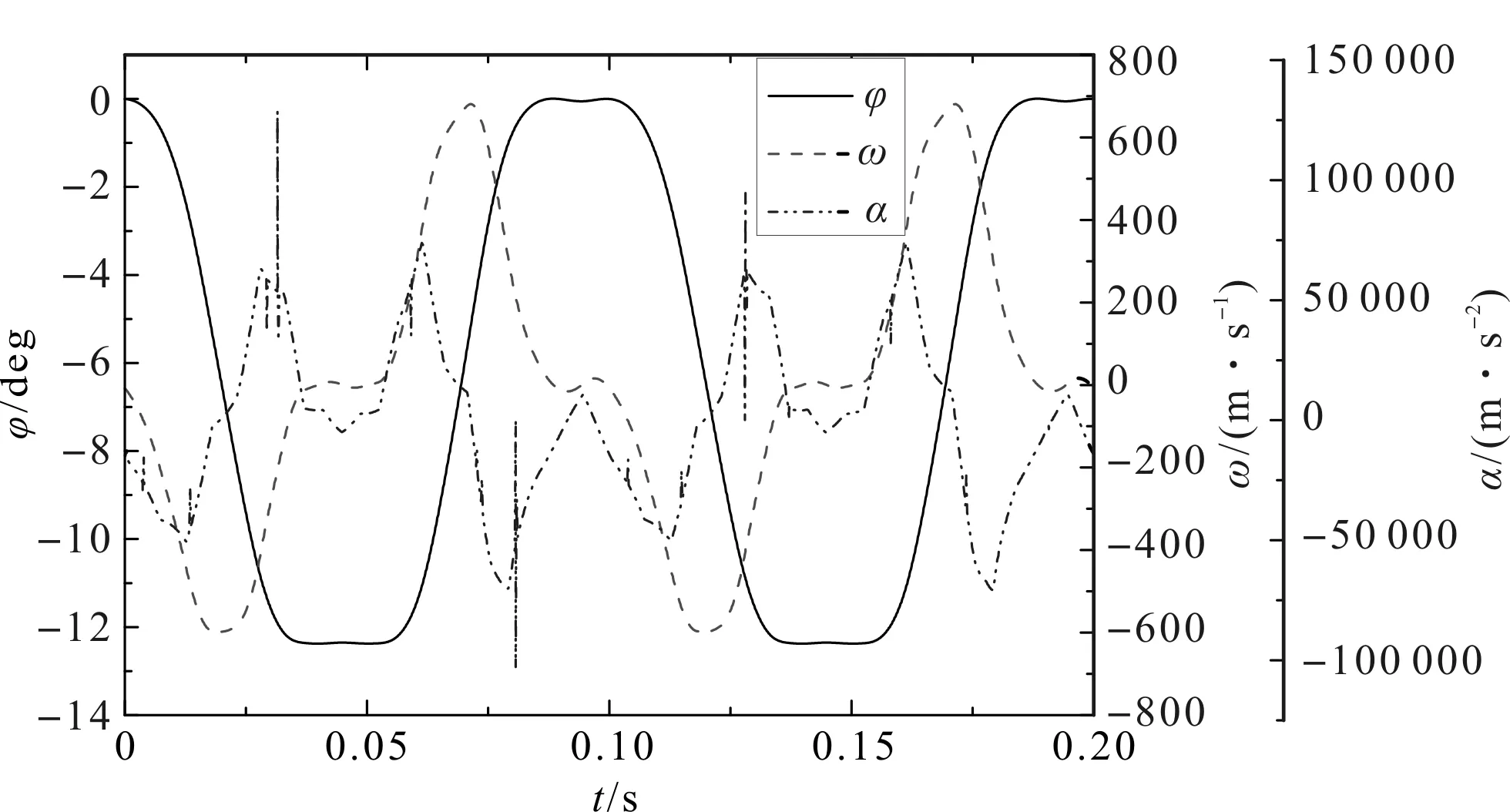
图7 摆杆角运动曲线
由图7分析可知:摆杆的摆动角度范围为0~12.4°,且两个极限角度位置的角速度和角加速度均为0,说明摆杆在摆动起止阶段也不存在冲击载荷,由此进一步验证了凸轮机构的高速无冲击特性。
4.3 开口动力学特性
笔者将由Step函数拟合的动态经纱张力加载至综框,对凸轮开口机构进行动力学仿真。
综框升降过程中,回综弹簧的弹力与变形关系如图8所示。

图8 回综弹簧形变与弹性力
由图8分析可知:在0.1 s内弹簧发生一次伸缩变形,最大形变量约145.6 mm,与之对应的最大弹性力约584.75 N,由虎克定律可计算出回综弹簧刚度约为4 016.14 N/m,与实际弹簧设计刚度K1(4 014.57 N/m)基本一致。
对于凸轮开口机构,在综框升降运动过程中,要求凸轮与滚子之间始终保持接触[11]。
滚子与凸轮在X方向的接触力仿真曲线如图9所示。
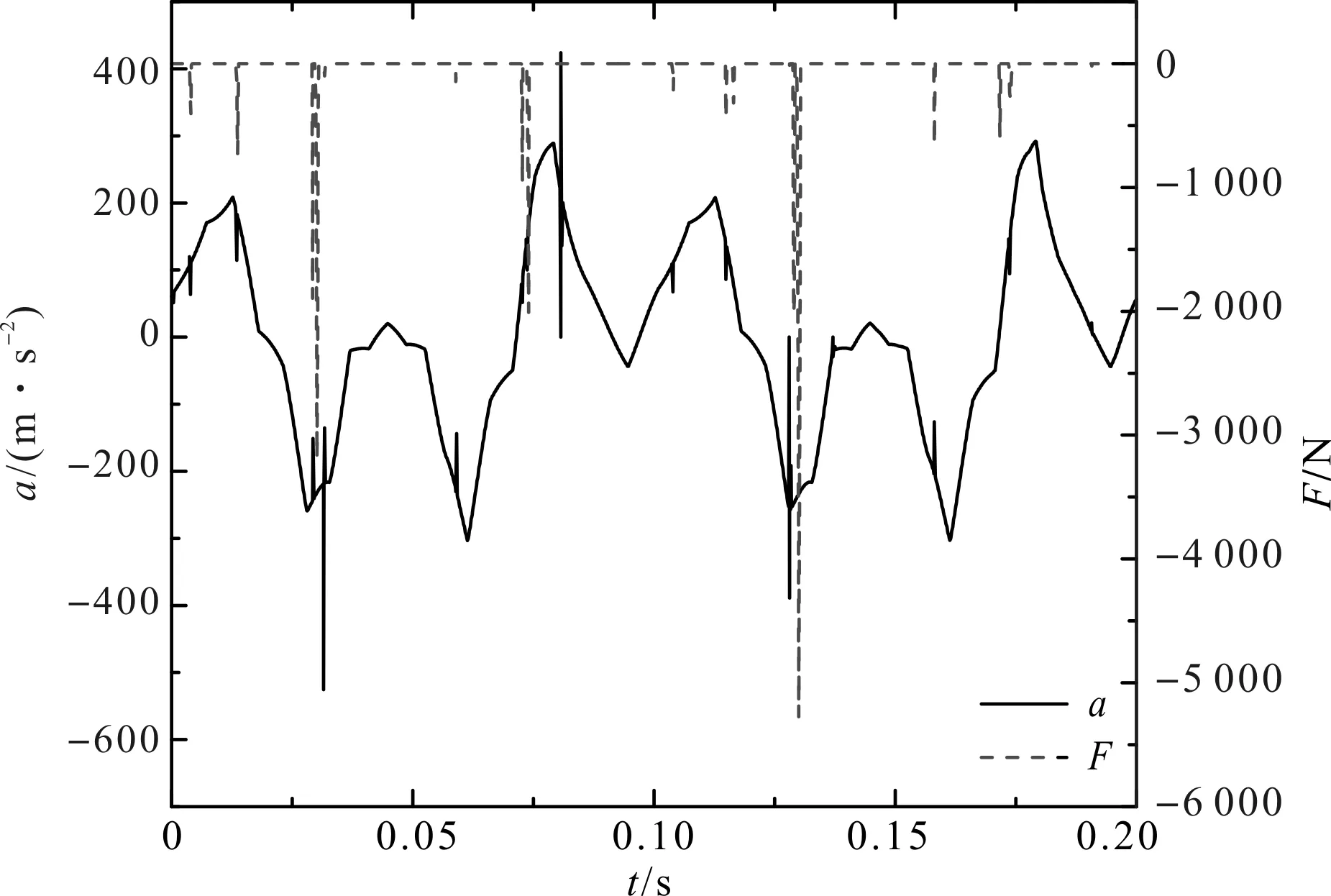
图9 滚子接触力与加速度
通过图9对比分析可知:在加速度波动瞬间,滚子存在较大接触力,但时间很短且次数不多,其余时间段的接触力基本为0,说明滚子加速运动过程相对平稳,不会与凸轮长时间发生较大的接触碰撞,满足滚子从动件的正弦加速运动要求。
5 结束语
随着现代机织技术的进步,对于凸轮开口的性能要求将愈来愈高。本研究通过理论推导、样机开发和动态仿真,设计了一种基于弹簧回综的新型消极式凸轮开口机构,并根据实际承载工况构建了力学模型和功能型样机,在此基础上将动态经纱张力引入了综框升降运动,在ADAMS/View环境下实现了凸轮提综和直吊弹簧回综的动态仿真分析。
研究结果表明:在综框行程约14.5 mm、摆杆角动程为12.4°时,机构运动学和动力学特性满足消极式凸轮开口工艺要求,验证了设计方案的的可行性。
该方案有效提高了凸轮开口过程的动力设计精度,对于消极式凸轮开口的设计创新具有重要参考价值。
