带传动装配张力的动态预测研究及其应用*

2021-01-22林晓涵王少杰

机电工程 2021年1期

林晓涵，王少杰，侯亮，杨峥，穆瑞

(厦门大学机电工程系，福建厦门 361005)

0 引言

装配质量对产品性能与品质有着重要的影响。如装配过程中存在的装配工艺、装配方法、装配精度的不规范操作，会直接影响产品的性能和质量。装配参数对产品性能和质量的影响通常情况下主要有3个方面[1-4]：(1)不合理装配导致系统工作不正常；(2)零部件配合不当增加了额外振动噪声；(3)不合理的装配改变了系统刚度、阻尼等固有特性，与其他零部件发生共振。

而在客车发动机总成生产过程中，带传动系统工作的稳定性直接影响到整车的NVH性能，特别是车内后排乘坐舒适性。其中，张力调整不当，会发生皮带滑移、跳带、磨损等状况，这是客车生产过程中导致NVH性能不达标最常见的原因。

带传动张力的调整不合理，不仅会影响原有的动力传递，导致其他系统工作的不正常，而且还会改变带传动的自振频率，增加与其他零部件发生共振的可能。因此，针对装配质量的研究，BOYSAL A等[5]基于非线性动态模型，建立了多目标优化模型，实现了对悬置软垫的制造及整车装配的优化；AHMAD A[6]、GONZALEZBADILLO G[7]等人基于虚拟现实技术对发动机装配线进行了动态仿真，评估了物理仿真引擎在虚拟装配应用中的性能，实现了发动机装配的效率提升及质量优化；ABELLANNEBOT J V等[8]分析了基于传感器的夹具优化配置、传感器的数量优化，综合误差传递理论和状态空间方程，实现了多工序制造、装配过程的产品质量预测和误差补偿。

保障装配质量不能仅依赖于零件公差设计，还必须通过测量与调整等装配工艺来共同实现[9]。由于我国客车装配生产还是以人工为主，容易出现张力的测量与装配精度低的问题。为避免张力不当导致的质量性能问题，进行张力预测是能够及时发现问题，并采取相关调整的有效途径。进行张力预测需要从采集到的信号中建立模型，以估计装配的参数。

传统的张力预测方法是建立回归数学模型，需要分析现象之间相关的具体形式，并用数学公式表示出来。NESTOR A[10]通过理论分析，建立了一种同步带齿型载荷分布模型，并通过理论结果和实测值的对比，分析验证了模型准确性；CEPON G[11]将阻尼引入了柔性多体皮带传动模型中，通过数值分析和实验研究了皮带传动系统的张紧力在不同预紧力下的振动变形特性；MECKSTROTH R J等人[12]基于显式积分有限元理论对发动机带传动系统进行了仿真分析，通过对系统中张紧器摆动量、带张力、皮带的振动、皮带滑动率等的分析计算，实现了发动机的装配减振优化设计；但这种方法不但复杂难以求解，且建模过程也比较耗时。

所以性能更优的人工神经网络被越来越广泛地应用于模式识别、预测估计等复杂问题上[13]。将神经网络应用于工业装配质量控制上，在这方面国内已有一些学者开展了相关研究。GUH R S等[14]利用BP神经网络和专家系统，对产品制造装配过程的控制图模式进行了识别和分析；陈勤和[15]建立了支持向量机和BP神经网络两种预测模型，实现了通过螺栓拧紧关键因子对发动机前期装配整体质量的预测，并根据预测发动机的振动量，及时发现了装配质量问题，节约了生产时间和成本；赵明志[16]以某变速箱生产为应用背景，针对变速箱短期的装配质量预测问题，建立了基于PSO-BP的神经网络装配质量预测模型；张根保等[17]以某磨床的砂轮架装配为例，验证了PSO-BP神经网络对产品装配质量预测模型的有效性。

神经网络在工业装配预测上的成功案例证明了其可行性和有效性，但将其应用于带传动张力装配预测方面的研究目前还较少。

在带传动张力的智能控制中[18]，牟学鹏[19]介绍了一种带式输送机张力智能监控系统，通过在带传动系统中安装张力传感器，可以实时反馈当前张力是否处于理想范围内；董立红等[20]同样针对带式输送机进行了研究；PAN[21]研究了使用非接触式光电角度电位器和直流无刷电机的主动送线式电子张力控制器，并基于模糊控制PID算法给出了仿真条件下的控制参数和系统阶跃响应曲线。

这些研究的基本思路都是需要先获取张力值，从而对张力实施调控。这类带式输送机采集的数据多来源于张力传感器、电控系统中的电流信号、控制系统行为数据等。但是这些方法对于空间容量狭窄的客车带传动系统并不适用。

综上可知，围绕大型带式输送机张力控制和神经网络预测方法的研究，相关学者已经取得了很多成果，并得到了好的效果；然而针对客车的带传动，目前还没有很好地解决数据采集和张力预测的问题。

本文提出一种基于神经网络和振动信号分析的带传动张力测量和预测方法，首先进行台架稳态张力测量及振动信号采集试验；在试验台架上模拟带传动系统，采集不同张力下的振动信号作为神经网络训练和测试的数据基础，分别建立BP、RBF、GRNN 3种常见神经网络的预测模型；最后分析并评估网络模型对台架带传动张力预测的效果。

1 神经网络的张力动态预测方法

带传动张力预测方法过程如图1所示。

图1主要包含以下几项内容：

(1)根据客车带传动工作特点，本文设计带传动台架试验，采集试验数据；从台架上采集到不同张力状态下的振动信号经过数据处理分析，生成网络模型的输入；

(2)基于神经网络的张力预测，是通过建立振动信号与张力值之间的映射关系来实现的。神经网络建模作为关键步骤，需要对其设定合适的网络参数，并输入样本集进行训练；训练完成的网络模型可以实现特征集到张力值的输入输出计算，即张力的预测；不同的神经网络采用不同计算方法，使用时可参考训练结果进行选择。决定系数、相对误差等作为评判网络模型性能的指标；

(3)将上述试验和建模方法重新应用于客车工程实践中，使用客车案例验证所提方法的可行性和有效性。台架带传动和客车带传动实际情况存在差别，但整体工作方式相近，对照台架试验对客车带传动振动数据进行采集。

客车数据同样需要经过数据采集、数据处理阶段，对建立的神经网络模型进行重新训练测试，实现对张力的预测。

图1 带传动张力预测方法过程

在工程应用中，可根据皮带型号、使用场景、性能要求等对工作张力设定推荐值和合理波动范围。因而，一般可以定义张力大小范围的3个区间：合适区间、过小区间和过大区间。当神经网络给出预测张力值时，可以根据设定的阈值判断张力状态，并由此做出继续运行、建议调整、停机维护等指令。

2 台架试验的张力-振动信号关系

2.1 台架试验设计

本文通过台架模拟带传动装配状态，并采集不同张力下的振动信号作为神经网络的训练测试集。该试验采用机械故障综合模拟实验台(MFS-MG)，带传动主动轮通过电机驱动转动，主动轮与从动轮通过皮带直接连接带动。试验相关设备主要包含LMS数据采集系统、三向加速度传感器、Polytec激光测振仪和音波式张力计等。

台架试验测点布置图如图2所示。

图2 台架试验测点布置图

在带传动系统中，主要检测皮带的振动、主动轮的振动和从动轮的振动，如图2(a)中所标记的1、2、3点。1、3点以邻近静止点的振动近似替代主、从动轮的振动；2点测量皮带的横向位移信号，使用非接触式激光测振仪。

在使用激光测振仪时，应使激光聚焦，并垂直对准皮带跨度中心点。试验的台架设备置于光学平台上，起到一定的隔振作用，保障振动信号的采集不受外界因素干扰。

考虑到工程实际中，由于皮带自身伸缩特性及其他外界因素干扰，在静态下调节的张力和稳定运转后停机测量的张力可能出现偏差。所以张力的调整需要经过预调及稳定运转校正环节，以保证测量张力值的有效性，即训练标签的准确性。不同张力工况通过从动轮端的千斤顶螺栓调节跨距实现，并使用测量精度比车间常用的挠度法更精确的音波式张力计对张力进行测量[22]。笔者分别将带传动系统张力设为210 N、240 N、270 N、300 N、330 N、360 N、390 N，采集这7种工况下的振动信号，具体步骤如下：

(1)张力预调，通过旋动千斤顶螺栓控制带传动跨距，使用音波式张力计测量固定测点的张力值；

(2)固定好后启动电机，使皮带运转一段时间，并获得均匀受力；

(3)使用张力计测量同一点的张力，验证张力值的稳定性，当皮带运转一段时间后测点的张力值与预调值一致时进入振动信号采集阶段；否则重新调整张力值。

2.2 数据处理与分析

采集到的原始信号转变成神经网络的输入需要经过数据处理、特征提取、特征筛选几个数据分析步骤。

信号处理流程如图3所示。

图3 信号处理流程

通过对比不同工况下时域、频域的振动信号可以发现：(1)在时域上，不同张力下其表现在振动信号的振幅均方根值、最大峰值等统计参数存在明显区别；(2)在频域上，不同振动信号表现在驱动频率与被驱动频率上的幅值相差较多。

因此，笔者从振动信号中提取了方差、标准差、偏度、均方根、峰峰值、均值、峰度、波峰因数、脉冲因子等9个常见时域特征，主动轮转速频率1阶～4阶谐波下峰值、从动轮转速频率1阶～4阶谐波下峰值8个频域特征。而台架试验共采集7个通道的不同振动数据，故最终得到7×17维特征。

笔者采用Fisher准则[23,24]对119维特征进行贡献量的排序与筛选，标准化并平均特征在不同类别的Fisher比，得到特征筛选的判定，如图4所示。

图4 特征筛选的判定

笔者取最终结果大于0的前38维作为敏感特征集，为后续网络模型的训练测试提供数据基础。

3 神经网络的张力预测

神经网络的多层感知拓扑结构，特别适用于处理多因素、多条件等模糊问题。神经网络作为回归预测模型时，具有很好的非线性映射能力，建模简单便捷，能够处理复杂数据等优点。已有研究表明，相较于传统的回归方法，神经网络的性能更优。因此，此处笔者选取了较为经典的3种回归神经网络进行测试比较。

3.1 神经网络算法简介

(1)BP神经网络。

BP(back propagation) 神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络[25]，其拓扑结构如图5所示。

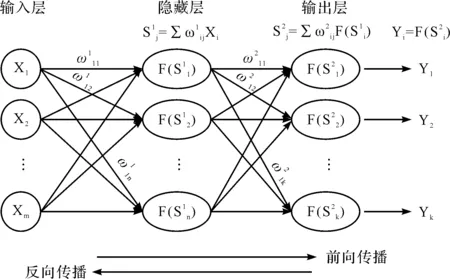
图5 BP神经网络拓扑结构

图5中，主要学习过程分为正向传播和反向传播两个阶段。通过一次正向传播和一次反向传播，网络的参数就会更新一次。正向传播和反向传播不断往复进行并更新网络参数，直到达到训练精度或训练次数等要求，训练停止。

(2)RBF神经网络。

径向基函数(radial basis function)是某种沿径向对称的标量函数，通常定义为空间中任一点x到某一中心xc之间欧氏距离的单调函数,可记作：φ(‖x-xc‖)；但其作用往往是局部的，即当x远离xc时，函数取值很小。

最常用的径向基函数是高斯核函数，即：

(1)

式中：xc—核函数中心；σ—函数的宽度参数，控制了函数的径向作用范围。

RBF与BP的区别主要在于训练方法上。BP激励函数一般为sigmoid函数，通过不断调整神经元的权值来逼近最小误差；而RBF激励函数一般为高斯函数，通过对输入与函数中心点的距离直接计算权重。

RBF神经网络拓扑结构如图6所示。

图6 RBF神经网络拓扑结构

图6中，RBF网络的基本思想就是用RBF作为隐单元的“基”构成径向基层空间，这样就可以将输入矢量直接映射到隐空间，而不需要通过权连接，其变换是非线性的[26]。当RBF的中心点确定以后，这种映射关系也就确定了。相较于BP神经网络，RBF具有最佳逼近、分类能力好、学习过程收敛速度快，以及可克服局部最小值问题等优点[27]。

(3)GRNN神经网络。

GRNN(general regression neural network)广义回归神经网络是径向基神经网络的一种， GRNN神经网络拓扑结构如图7所示。

图7 GRNN神经网络拓扑结构

图7中，GRNN与RBF的区别在于多了一层求和层，而去掉了隐含层与输出层的权值连接，即由输入层、模式层、求和层、输出层组成。GRNN具有较强的非线性映射能力和学习速度，样本数据少时，预测效果好，还可以处理受外界影响的非线性因素[28]。

神经网络建模需要设置几个重要的调节参数，例如BP神经网络的网络结构、训练目标、学习率、激活函数，RBF和GRNN的径向基扩展速度等；通过特征集的训练对神经网络模型参数进行调整。

各神经网络参数调整如下：

BP网络设置2个隐藏层，各5个神经元，隐藏层训练函数为logsig,训练精度为10-6，学习率为0.01；RBF扩展速度设为1.8，GRNN光滑因子0.5。

3.2 神经网络模型的评价指标

为评估回归网络模型好坏，此处使用3个指标作为评判标准。其中，均方误差、均方根误差、决定系数用于评价对比同一数据间不同神经网络的测试结果；同时，平均相对误差能够更好地对比台架试验数据与实车数据验证之间的结果。

(1)RMSE(root mean squared error)，均方根误差是均方误差的开方值，能够将得到的误差结果与输入数据保持在同一量级，更便于直观地描述和判断误差的大小。RMSE的值越小，说明预测模型描述实验数据具有更好的精确度。

其求解方程如下式所示：

(2)

(2)R2(R-Squard)。决定系数，也称为拟合优度，其表达式为：

(3)

式(3)中，分子部分表示真实值与预测值的平方差之和，分母部分表示真实值与其均值的平方差之和。R2的取值范围为[0，1]，决定系数越大，自变量对因变量的解释程度高，所引起的变动占总变动的百分比越高。

(3)T(Time)。建模训练时间，以时间评估神经网络的模型复杂度以及计算速度。时间越短，在工程应用上就越能节约时间成本。

3.3 神经网络的测试结果分析

笔者将台架试验中每组工况数据分割成100组样本，则7个张力工况共要得到700组数据；从中得到的特征集按4:1的比例分成训练集和测试集，即560组训练样本，140组测试样本；分别建立BP、RBF、GRNN 3种神经网络的回归模型，将打乱的训练集输入神经网络进行训练，测试集即可作为神经网络预测能力的验证指标。

3种回归神经网络预测结果如图8所示(其中：F—皮带张力)。

图8 3种回归神经网络预测结果实心圆—真实值；空心圆—张力预测值，空心圆偏离实心圆越远，代表预测误差越大。

笔者整理了各神经网络模型在台架试验的张力预测上的各项评价指标，不同神经网络张力预测的结果对比如表1所示。

表1 不同神经网络张力预测的结果对比

根据图8与表1可知：

(1)图8(a)中，BP神经网络预测得到的数值能够较集中地在期望值附近，决定系数R2为0.998 0，表明建立的模型中自变量与因变量相关性较好；均方根误差RMSE为2.704 5，整体预测效果较好；BP神经网络在张力330 N及张力360 N时出现相对较多偏离点，在中间段张力预测表现较好。模型计算时间为2.658 5 s；

(2)图8(b)中，RBF神经网络曲线中决定系数R2为0.956 3。在张力为360 N时出现预测异常点，导致整体RMSE较大，为12.542 6；RBF预测精度不如BP神经网络，但其计算时间0.884 6 s比BP的2.658 5 s短。从RBF在不同张力样本上的预测结果知，其误差分布均匀；

(3)图8(c)中，在GRNN网络模型测试中，预测值基本落在期望值上，得到的决定系数R2为0.999 9，接近于1，证明该模型中自变量与因变量的相关性为3种神经网络中最好的；得到总均方根误差0.443 2最小，模型计算时间0.250 4 s最短。

4 基于客车试验的预测方法验证

笔者从某带传动系统上采集获得验证数据。试验在整车静止时发动机怠速800 r/min工况下进行。

客车带传动信号采集如图9所示。

图9 客车带传动信号采集

图9中，与台架试验方案相同，客车数据采集使用激光位移传感器测量皮带横向振幅，使用三向加速度传感器测量带轮附近点以替代带轮振幅。在830 N～133 0 N张力区间内，以50 N等间距调节张力，分别测量采集带传动振动信号；采样频率1 024 Hz，采集时间500 s，以5 s为单位时间分割数据，则同一状态下产生100组样本。

同样，笔者利用前述方法对数据进行处理和特征提取，建立神经网络模型，训练并得到3种神经网络在客车带张力预测的应用验证，如图10所示。

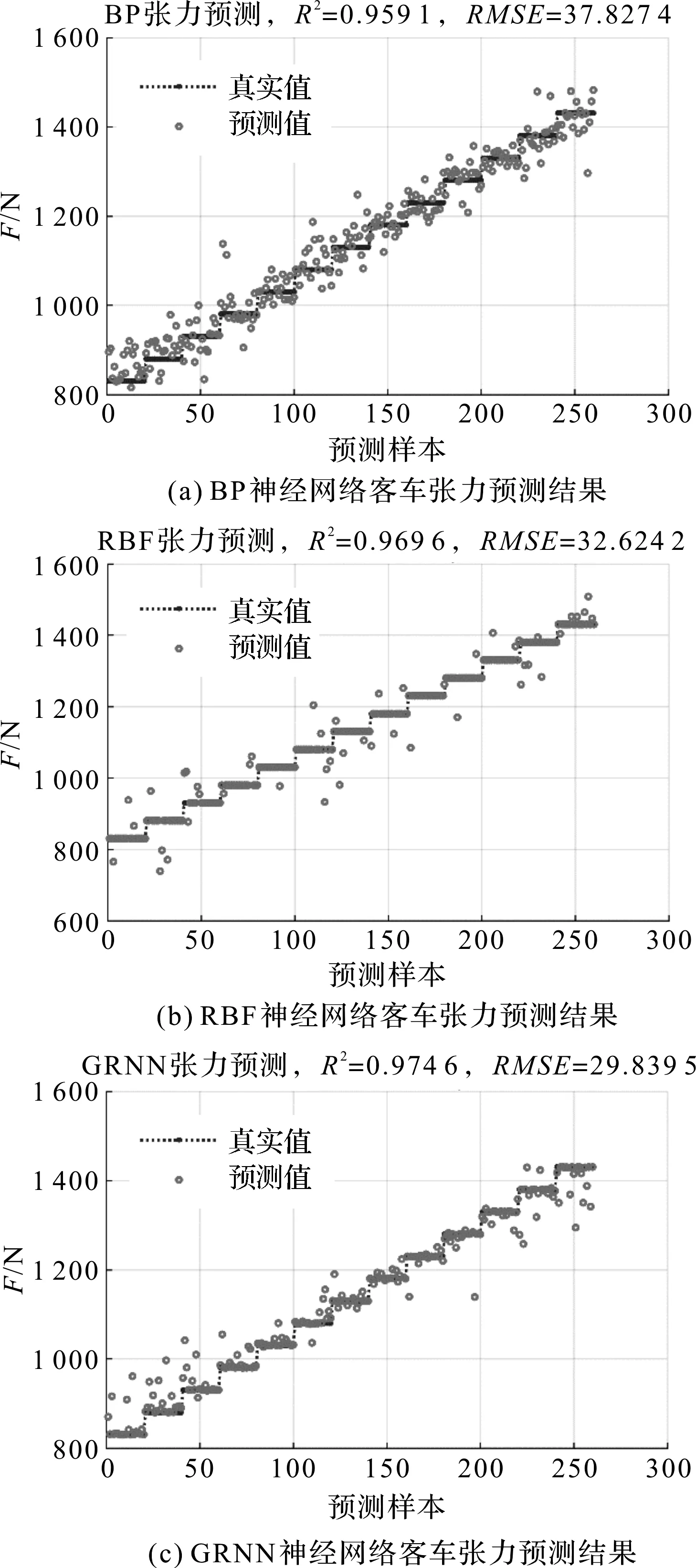
图10 3种神经网络在客车带张力预测的应用验证

笔者整理了各神经网络模型在客车张力预测验证上的各项性能指标，不同神经网络在客车张力预测的验证结果如表2所示。

表2 不同神经网络在客车张力预测的验证结果

观察图10拟合曲线及表2，并结合台架建模时的结果进行比较，可得出以下结论：

(1)BP、RBF、GRNN 3种神经网络在建立客车张力预测模型时得到的决定系数相差不大，但均达到了0.95以上，拟合相关性较好；

(2)在3种神经网络中，GRNN表现最好，其得到的决定系数最高，为0.974 6，得到的均方根误差最小，为29.839 5，建模时间最短，为0.027 7 s。这一对比结果与台架建模时的结论一致；

(3)虽然3种神经网络得到的决定系数相近，但从预测图像上相较来说，BP神经网络预测值落点明显偏离真实值的数量较多。以偏离真实值±30 N内为可接受的张力预测误差范围，统计不同神经网络预测值有效的概率可知，在260个测试样本中，BP预测值有效个数为175个，有效率67.31%；RBF预测值有效个数为222个，有效率85.38%；GRNN预测值有效个数为224个，有效率86.15%。由此可见，BP神经网络模型在张力预测上的应用性较差；

(4)张力预测模型的决定系数、均方根误差结果均比台架建模时得到的结果更差。原因是由于客车实际工况复杂，导致采集到的数据中包含无用噪声，影响了后续特征提取及模型训练精度。

综上可知，RBF和GRNN神经网络在决定系数、均方根误差、预测值有效率上更能满足工程应用要求，均能作为张力预测的网络模型；若应用于批量预测上，GRNN在计算速度上表现更优。