矢量舷侧阵平台自噪声空域滤波抑制方法

方尔正， 孙纯， 桂晨阳

(1.哈尔滨工程大学 水声技术重点实验室，黑龙江 哈尔滨 150001； 2.海洋信息获取与安全工业和信息化部重点实验室(哈尔滨工程大学)，黑龙江 哈尔滨 150001； 3.哈尔滨工程大学 水声工程学院，黑龙江 哈尔滨 150001)

近年，新型无人水下潜航器(unmanned underwater vehicle, UUV)作为高技术的水下无人作战平台，在复杂海洋环境中工作时具备低消耗、隐蔽性、机动性等特点，已在水下目标侦察与防御、海洋科学考察与试验等领域发挥了重要作用[1]，是遂行水下无人攻防作战任务的重要保障之一。但目前水下目标隐身技术迅速发展，使得潜艇和水面舰艇的辐射噪声水平不断降低，从而导致水下航行器对其探测难度不断提高，故现阶段迫切需要大幅度提高UUV的目标探测距离，以保证对远场目标的发现、跟踪以及精确打击。提高UUV探测距离的有效手段之一是降低工作频率，但工作频率的降低受UUV传统头部平面基阵几何尺寸限制，并且会引起空间增益和估计精度的下降，故往往会在其舷侧加装舷侧阵，将若干个声呐纵向排列形成两列长线阵，这种布放形式不占航行器空间位置，也不影响其水动力学性能，同时能够增大水声探测系统基阵有效孔径并尽量降低工作频率[2]。

由于舷侧阵直接安装在航行器壳体上，平台本身的近场干扰很强，主要包括平台振动引起的噪声、流噪声和螺旋桨辐射噪声等[3], 这些辐射噪声的频率接近低频声呐的工作频率，故无法用简单的滤波算法来消除，会降低舷侧阵声呐系统的作用距离、目标识别概率及精度。由于舷侧阵基阵的长度大约占艇长1/3～2/3，平台振动引起的噪声就是由艇内安装的众多机械设备运行时对艇体产生的激励带来的，会对目标信号构成本地强干扰，在航行器低速航行时影响最为严重。平台振动引起的噪声主要包含2个部分[4]: 1)由航行器内部机械振动通过壳体、管道、基阵安装结构传至各水听器，这部分噪声可以通过在声呐与舷侧之间安装减振隔振结构降低其影响；2)由航行器内部机械振动在其周围激起声波，声波直接传至各水听器, 它属于近场辐射噪声，本文针对的就是这部分噪声。

对于平台振动噪声，国内外现有的处理方式大多是采用自适应噪声抵消[5]、自适应波束形成[6]或盲信号分离[7]等基于平面波传播的抑制或抵消的方法；文献[4]则是根据平台噪声特性选用具有更低旁瓣的窗函数进行数据截断来提高系统的信号检测能力。但由于振动干扰传播信道和产生机理十分复杂，上述处理方式的效果都很有限，不能有效提高声呐目标方位估计的性能。空域矩阵滤波技术[8-9]是一种新兴的对阵列信号进行预处理的技术，通过对空间方位设置通带和阻带，得到一个空域矩阵与阵列接收数据相乘，来保证通带区域内目标信号最大程度无失真通过的同时，抑制阻带区域的强干扰，能获得更高精度的平面波方位估计，为平台近场辐射噪声抑制提供了可行途径。由于空域矩阵滤波器滤波后的数据仍为阵元域，所以此类滤波器可以用在很多目标定向或定位算法之前[9]。

本文将空域矩阵滤波技术、矢量信号处理技术以及平面波方位估计技术结合，共同设计抑制平台强噪声干扰的空域矩阵滤波器，给出空域矩阵滤波器的最优解及推导过程，并基于矢量舷侧阵的最小方差无失真响应(minimum variance distortionless response，MVDR)波束形成算法对滤波前后的远场弱目标信号进行波达方位(direction of arrival，DOA)估计的仿真，对比分析得到滤波器性能。

1 矢量舷侧阵信号处理模型

对于矢量舷侧阵来说，被探测目标信号源距阵列的距离D≥L2/λ，满足远场条件，辐射的声信号经过远距离传播到达基阵后能量很小，为远场弱信号，而平台辐射噪声与舷侧阵声呐基阵的距离较近，能量相对远场目标来说比较强，应该视为近场强干扰[10]。为便于分析，将舷侧阵抽象为均匀线列阵，取航行器左右舷中任意一侧的舷侧阵进行信号处理模型的建立。假设P个水下目标、Q个近场辐射干扰源(为点干扰)、基阵位于同一水平面，矢量水听器阵是由M个水声换能器构成，各个阵元等间距布放，间距为d，阵的总长度为(M-1)d，建立如图1所示二维UUV舷侧阵信号处理模型。

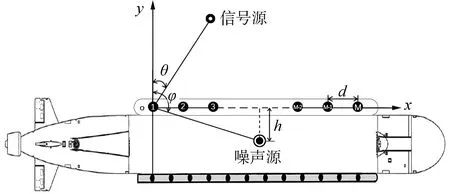
图1 UUV舷侧阵信号处理模型Fig.1 Signal processing model of the flank array

则接收阵列信号模型可用矩阵形式表示为：

X(t,f)=As(θ,f)Ss(t,f)+An(φ,f)Sn(t,f)+

N(t,f)

(1)

式中：

(2)

式中：Ss(t,f)、Sn(t,f)分别为目标信号源矩阵和平台噪声干扰源矩阵；As(θ,f)、An(θ,f)为远场平面波阵列流型矩阵和近场球面波阵列流型矩阵;N(t,f)为加性高斯环境噪声矩阵；θ=[θ1…θP]、φ=[φ1φ2…φQ]分别为目标信号与噪声的入射角度。信号源和干扰源到接收阵的方向向量：

其中：

式中cz代表水下声速，cz=1 500 m/s；cn代表空气中声速，cn=340 m/s。

由于声压与振速的关系：

此时声矢量传感器的阵列流形为：

代入式(1)中得到矢量阵接收阵列信号模型：

Xv(t,f)=Asv(θ,f)Ss(t,f)+

Anv(φ,f)Sn(t,f)+Nv(t,f)

(3)

其中的阵列流型矩阵和对应的方向向量变为：

式中⊗为Kronecker积的运算符。

2 空域矩阵滤波器设计

首先针对声压阵接收数据设计中心频率为f的空域矩阵滤波器H(f)M×M，再推广到矢量阵。滤波后的输出为：

Y(t,f)=H(f)X(t,f)=H(f)As(θ,f)Ss(t,f)+

H(f)An(φ,f)Sn(t,f)+H(f)N(t,f)

(4)

滤波器的设计需将全空间划分成通带区域ΘP和阻带区域ΘS，其分别对应的阵列流型矩阵为：

式中：a(θp)和a(θs)分别代表通、阻带离散化后的方向向量；P和S分别为通、阻带离散化的点数。

由于平台强干扰来自于某确定的小范围方位内，因此可以选择对窄阻带设置零响应约束，求解阻带零点约束的空域矩阵滤波器来消除近场干扰的影响。故建立如下的最优化问题[11]：

其中约束条件H(f)VS(ΘS)=0M×S可以表示为：

因此最优化问题转化为：

(5)

为方便求解，将H(f)、VP(ΘP)、VS(ΘS)简记为H、VP、VS，通过构造Lagrange函数的方法解上述最优化问题，式(5)对应的Lagrange函数为：

(6)

式中，λ和δ均为Lagrange乘子，λ=[λ1…λS] ,δ=[δ1…δS]。

由于目标函数和约束条件都是严格的凸函数，故对于任意λ和δ，对式(6)Lagrange函数求偏导等于零的解即为最优化问题的全局最优解，即：

(7)

(8)

式中I为M×M维单位向量。

对于矢量阵，结合矢量信号处理的方式可以得到通阻带阵列流型矩阵的矢量表达形式VPv和VSv：

式中：

因此对于式(8)中的滤波器的矢量表达式为：

(9)

则最终滤波输出为：

Y(t,f)=Hv(f)Xv(t,f)=Hv(f)Asv(θ,f)Ss(t,f)+

Hv(f)Anv(φ,f)Sn(t,f)+Hv(f)Nv(t,f)

(10)

3 平台自噪声抑制算法仿真

首先分别给出空域矩阵滤波器作用前后基阵近场和远场方向向量的归一化指向性图，通过指向性对比图来验证滤波器的作用。

由于UUV 尺度有限，限制了其舷侧阵的孔径。现在使用的 UUV 长度一般不会超过15 m。故考虑一个由16个水听器组成的舷侧阵基阵，信号为1 200 Hz的窄带信号，阵元间距为半波长，阵总长9.375 m。平台噪声干扰源距阵列1 m，为部分连续谱加线谱信号；目标信号源为满足远场条件的平面波信号。滤波器设计通带ΘP=[-180°,120°]∪[140°, 180°]，阻带ΘS=[120°,140°]。

从图2中可以看出，经过滤波器处理之后，基阵近场方向向量的指向性幅度在设定的阻带ΘS=[120°,140°]内大幅下降，即空域矩阵滤波器对设定阻带内的近场干扰噪声有明显的抑制作用；而对于基阵远场方向向量的指向性图，从图3中可以看出在设定的通带范围内是几乎没有变化的，即可以保证通带范围内的远场信号无失真通过。这里的指向性图仿真采用的是声压阵，故存在左右舷模糊，即关于90°/-90°的指向性对称，后续采用矢量阵即可消除左右舷模糊。

图2 滤波前后近场指向性图Fig.2 Directivity of near-field before and after filtering

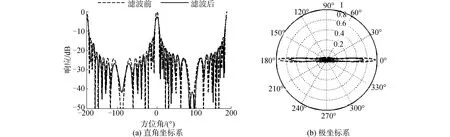
图3 滤波前后远场指向性Fig.3 Directivity of far-field before and after filtering

目前的声呐系统大多数情况下都采用波束形成算法进行信号检测，对于阵列和阵元布放形式固定的舷侧阵，最小方差无失真响应(minimum variance distortionless response，MVDR)波束形成算法较为常用且可靠。由于空域矩阵滤波器滤波后的数据仍为阵元域，故可直接用于后续MVDR算法。MVDR波束形成器的输出功率表达式为：

(11)

信号的波达方位可通过搜索上式的峰值位置来确定。R=E[YYH]为接收数据协方差矩阵，当采样快拍数N→∞时，可采用极大似然估计下的输出数据外积的统计平均值来代替：

(12)

在前述基阵指向性仿真条件的基础上，采用矢量水听器，设置远场目标信号、近场平台干扰噪声以及环境背景噪声，进行MVDR算法DOA估计的仿真。设目标信号的入射方向为25°，信噪比SNR=10 dB，平台干扰入射方向130°，干信比SIR分别为-100、-140、-150、-170 dB。图4给出了仿真结果。

从图4可以看出，当SIR=-140 dB时，滤波前的MVDR算法勉强能够定位出信号的来波方向，但由于近场平台噪声的强干扰，会在非目标来波方位出现幅度较高的假目标峰，而滤波后再进行MVDR算法处理的结果仅在目标方位出现单峰，消除了平台噪声强干扰带来的影响；之后随着平台噪声的增强，SIR逐渐降低，滤波前的MVDR算法受噪声干扰的影响愈加严重，显然已丢失目标方位，无法检测，而滤波后的MVDR算法依然具有非常好的信号检测和估计能力，但性能逐渐有所下降；当SIR降低至-170 dB时，可以看出空域矩阵滤波器的能力达到下限，滤波前后MVDR算法均失效。

图4 不同信干比条件下的DOA估计结果Fig.4 Results of DOA estimation under different SNR conditions

在此利用最高峰的幅值(dB-1)与K个次高峰平均幅值的差值来得到输出信干比，等价于：

(13)

式中:P(θi)为波峰最高的疑似目标方位的波束输出功率；P(θk)为波峰高度仅次于θi的K个干扰目标方位的波束输出功率；[∑P(θk)/K]为平均干扰功率，当SIRout大于某一阈值时，便认为检测到目标信号。在此设阈值为7 dB，K取为3，图5给出了通过200次蒙特卡洛仿真计算得到的输入与输出信干比之间的关系曲线。

为了得到空域矩阵滤波后MVDR算法的方位分辨能力，考虑临近双目标信号入射的情况。仿真设置SIR=-140 dB，目标信号方位θ1=25°,θ2=28°，30°，35°，40°。如图6给出了仿真结果。

图5 输入与输出信干比关系Fig.5 Relationship between input and output SIR

从图6可以看出，空域滤波处理后不仅能消除平台噪声强干扰带来的影响从而检测出正确的目标信号方位，而且具有较强的方位分辨能力，能够分辨出2个方位很相近的声目标，分辨极限为5°。

图6 滤波后算法的方位分辨力Fig.6 Azimuth resolution after the filtered algorithm

4 结论

1)设计的空域矩阵滤波器通过作用于信号方向向量对通阻带产生了预期的无失真通过或抑制的效果。

2)空域矩阵滤波器作用于阵列数据后再用于MVDR波束形成算法，平台自噪声带来的强干扰能够被很好的抑制，输出信噪比以及信号方位分辨能力得到了有效的提高。

3)该方法为后置信号处理创造了条件，进而应该能够提高水下航行器舷侧阵声呐系统的工作性能及作用距离。