闭环增益成形算法下的航迹保持控制
2021-01-22韩旭张显库
韩旭, 张显库
(大连海事大学 航海动态仿真与控制实验室,辽宁 大连 116026)
无人船是目前热点研究课题之一,其实现需要航迹保持、态势分析、路径规划、通讯、故障处理等多种技术手段的协同,其中航迹保持是整个控制系统中的底层技术,其他技术大多可以看作航迹保持基础上的技术叠加,因此对航迹保持控制方法的研究具有较大的现实意义。文献[1]将船舶航迹保持控制分为“间接式”和“直接式”两类,其区别在于执行器输出的取得是否经由航向保持控制。通常认为直接控制较间接控制更准确,间接控制较直接控制更易于理解和应用。由于在航向保持方面已有丰硕的成果[2-4],基于航向保持的间接式控制方法在应用层面仍为主流,但在研究层面,一方面对间接式控制的研究热度有所下降,另一方面有将航迹保持控制研究过度复杂化的倾向,这不利于现阶段间接式自动舵的研发。
直接式航迹保持算法的研究目前集中在动力定位问题上,通常做法包括基于Lyapunov定理设计控制器[5]、使用模型预测控制[6]、智能控制[7]等。间接式航迹保持算法主要依赖LOS算法,文献[8-10]结合LOS算法,分别用预测控制、滑模控制与变增益内模控制对间接式控制中的航向保持部分做了改进。Carrot following是一种最简洁的间接式航迹保持控制算法,从原理上属于LOS算法中的一类,其与LOS算法的区别在于设计控制率时只使用航向误差。优点是简单、直观、易于应用,但缺点突出,表现为鲁棒性差,参数调整随意,容易出现航迹震荡或收敛过慢,这主要是由算法在航向保持过程只使用比例控制造成的。而这一过程的控制正是简捷鲁棒控制方法[11]的长处。
简捷鲁棒控制方法是一套简单有效的控制方法,其特点是控制鲁棒性强,参数设置有依据而调整空间大,内容包括闭环增益成形算法[12]、镜像映射[13]、非线性反馈等算法[14],该方法在航向保持方面已取得了一系列的成果,但在航迹保持上的应用较少。文献[15]给出了一种基于闭环增益成形算法的直接式航迹保持算法,由于该算法的建立是基于船舶小扰动模型,只有在航迹误差较小时才适用,因此在没有给出目标航向获取方法的情况下,该算法并不能算是解决了任意位置的航迹保持问题。文献[16]对5种常见航迹保持方法做了总结和比较,结果是各自优缺点并存,较准确的控制方法的执行器动作迅速,执行器输出平稳的方法精确性较低。文献[17]对其中的LOS算法进行了改进,将原有的比例控制方法加入了针对海流的自适应补偿,文献[18]使用扩张状态观测器对其中LQR方法进行了改进,以补偿系统内部扰动和环境作用量。本文采用其中的carrot following方法,并将原文中对目标航向误差的纯比例控制用闭环增益成形算法替代,以此提高控制的效果和鲁棒性。然后对分离型积分项的稳态误差消除效果以及非线性反馈的节能效果做了测试,这些方法是以往在航向保持中较常见的方法,仿真结果表明这些方法在航迹保持中依然适用。
1 闭环增益成形算法与Carrot following算法
1.1 闭环增益成形算法
闭环增益成形算法源于鲁棒控制中的回路成形算法。对于如图1所示的闭环系统,图中d为低频干扰,Pd为某种低通传递函数,n为测量噪声,r为参考输入,y为实际输出,ym为测量的输出,ym=r-y-n,有:
(1)
式中:乘积项S称作灵敏度函数;乘积项T称作补灵敏度函数。
基于干扰d和噪声n的幅频特性,低阻的S和高阻的T是所希望的。注意到S+T=(I+PK)-1·(PK+I)=I,所以期望的S、T灵敏度曲线通常形式如图2所示,其中ωb称为交接频率。闭环增益成形算法的本质就是对补灵敏度函数T进行设计。若用N来表示T的设计阶数,设T1=1/(Nωb),通过简单计算即可将补灵敏度函数T中的控制器K解出:
(2)

图1 一类常见的闭环控制回路Fig.1 A common type of closed-loop control

图2 希望的灵敏度曲线Fig.2 Expected sensitivity curves
1.2 Carrot following算法
Carrot following算法通过引入路径上的虚拟目标点,得出船舶的目标航向,这一进程将不断重复,直到船舶接近路径并最终沿着路径前进。在这种方法中,将虚拟目标点称作carrot,船舶则不断跟踪目标,因此称作carrot following算法。考虑一条如图3所示线段WiWi+1,为跟踪路径需要2个步骤:1)确定航迹误差d,2)更新虚拟目标的位置:虚拟目标S位于距离Q点Δ处。基于S的位置更新船舶的期望航向ψd。寻找新ψd的过程一直持续到船舶达到Wi+1。

图3 Carrot following算法示意Fig.3 Carrot following algorithm schematic diagram
2 间接式航迹保持自动舵的设计
2.1 基于闭环增益成形算法的育鹏轮航向保持控制率
由文献[19]可以得到育鹏轮满载时的船舶参数,基于这些参数可以求得育鹏轮的旋回性指数K0=0.38,追随性指数T0=297.75,由此建立育鹏轮的Nomoto模型:
(3)
取高频渐近线斜率为-20 dB/dec,即取N=1,由文献[20]查表知,6级风(取风速12 m/s)下的海浪常见频率为0.43~2.8 rad/s,取交接频率ωb=0.067,这样海浪频率0.43时的增益略大于-7.3 dB,对海浪干扰的抑制较强,此时T1=15。设计补灵敏度函数T,将P的表达式代入T的表达式,即可得到执行器K:
(4)
这是一个PD形式的控制器,由文献[1]可知这种形式的控制器不能消除稳态误差,因此利用控制器的鲁棒性,在控制率中增加一个小的积分项,使系统到达稳态时能够逼近目标值。但需要注意的是这一积分项不宜过大,否则由于其在暂态过程的影响,在到达稳态的过程中将发生超调。此外,这是一艘大惯性船,由文献[21],可适当增大比例项以减小上升时间。经过以上改动后控制器可变为:
Kpid=3.63+0.001/s+783.55s
(5)
2.2 基于改进carrot following的间接式航迹保持算法
图4为间接式航迹保持控制示意,carrot following算法用于实现图中的航海计算和航迹控制部分,而航向保持控制部分的实现则由闭环增益成形算法实现。

图4 间接式航迹保持控制示意Fig.4 Diagram of indirect trajectory tracking control
在1.2节已给出目标航向的获取方法,但原算法有4个关键点没有说明或需要改进:1)没有进行转向点的设置和处理;2)参数Δ的选取缺乏指导;3)文献[16]原文中对航向保持简单使用了比例控制因而效果不佳;4)角度的表示不符合航海习惯。
针对这4个问题,本文给出了对应的解决方案:1)设航路点的到达判定距离为λ(或者叫起转距离),若距下一转向点Wi+1距离小于λ则改变航线。2)Δ和λ的选取应与船舶转向能力相关,因此也与航速相关,从经验上看,Δ取值通常略大于2倍船长,船速大时可适当增加,若Δ过大则暂态时间长,过小则会出现震荡,λ的大小大致为该速度下的旋回进距。3)使用闭环增益成形算法实现航向保持,航向误差为目标航向与当前航向的差值。4)角度修正到0°~360°,从而避免了传入信号和计算所需之间的偏差。相比原算法,本文增加了到达航路点的判断,基准点随航路点到达而切换,实现了带有转向的航迹保持。
3 算法改进及仿真验证
为使最终的航迹保持算法能快速而准确的跟踪目标航向,一个性能良好的航向保持算法是必须的,为此这里会先验证航向保持控制效果。
目前为止,在应用闭环增益成形算法进行航向保持时,在稳态误差的消除方面并不是很理想,引入积分项过大会导致超调,过小则不利于稳态误差的快速消除,为解决这一问题,本文采用积分分离型设计[22],即当航向误差小于某个阈值时启用积分项,而大于该阈值时关闭,这样就规避了积分项在暂态过程中的影响,因而可以加大积分项以尽快消除稳态误差,本文选取积分阈值为π/36,积分增益为0.005。
为解决控制器输出能量过大的问题,文献[23]给出了一种非线性反馈方法,较好地实现了控制能量与准确性的平衡。事实上由于船舶的运动特点,如果忽略掉死区问题和风流的影响,在任意运动状态下向某一方向打舵,船舶都会产生该方向的转艏加速度,因此对于航向保持问题,在不考虑快速性的情况下,只要执行舵角大小超过当时的直航压舵角就可以实现航向保持。基于这一认知,可以根据航向误差大小设计非线性函数,适度削减较大误差时的控制输入而不对较小误差时的控制输入做过多影响。本文使用的非线性函数为:
(6)
式中:c为调整参数,这里取为π/6;e为不大于π/2的航向误差,若e>π/2,则取e=π/2。
被控对象模型采用下式的响应型非线性船舶运动模型[11]:
(7)
式中:K0=0.38,T0=297.75,α=11.95,β=23 928.91。控制系统的总体结构如图5所示,其中航向保持子系统的内部结构可参考文献[19],不同之处只是控制器的设计以及一些参数的选取不同。

图5 控制系统总体结构Fig.5 Overall structure of control system
首先验证积分分离和执行器非线性处理在航向保持中的效果。设定航向保持的目标航向为30°,在系统中加入风浪干扰,假设定常风为蒲式6级(12 m/s),由文献[1]可计算得出横风时的等效压舵角为0.97°,将其作为定常干扰加入控制系统中以检验稳态误差消除能力,参照文献[19]加入浪力干扰,即白噪声驱动的二阶振荡系统,用它检验控制系统的鲁棒性和噪声抑制效果,噪声强度0.001,取样时间0.5 s,6级风下该二阶振荡系统为:
(8)
算法改进前后被控系统的航向和舵角输出如图6所示。可以看到,虽然上升时间较原来略长(从56 s增大到61 s),但操舵极值从23.5°降低到了15.5°,降低了执行器的耗能和磨损,而且由于可实行大的积分项,在不带来额外超调的同时,稳态误差的减小速率明显加快。因此预测改进控制器的航迹保持效果也会比改进前要好。
现在考虑航迹保持。为确定航迹保持中参数λ的大小,对所建立模型进行25°舵角的旋回实验,易得旋回进距约为480 m,为留有余量,这里λ取值为500。旋回舵角的选取说明:中国航海学会指出在航海实践中驾驶员进行转向时很少使用15°以上舵角,这一方面有助于防止横摇幅度过大,另一方面更大的舵角所带来的旋回改进效果有所下降。但这里选用25°作为限幅舵角,是希望留有安全余量,如果需要考虑避碰问题就需要打大舵角,因此这样设计舵角限幅是符合常识的。另一个航迹保持参数Δ的取值为500,预设航路点为(0,0), (1 500,1 500), (750,3 000), (-1 500,3 000), (0,0),初始航向0°,初始船位(0,0),航速17.5 kn,海浪的影响保持不变,将定常风的影响由风生流取代,由文献[24],干扰大小取向东0.4 kn。在以上参数设置下,航迹保持的仿真结果如图7、图8所示。图9对2次仿真的结果进行了对比,注意到其中航迹误差会突然增大,其原因是要转向时所追踪航线发生改变,因此这一误差会增大到参数λ的大小。
关于航路点的说明:仿真验证为展示转向、暂态和稳态的各个过程,航路点间的距离选取较近,而在实际航行中的航路点间间距通常较远,离开一定距离后,稳态时与上一航路点夹角较小,因此计算误差会随之增大。为应对这种情况,一个简单的解决方法在算法开始时检查录入的航路点,并对间距大于某个阈值的相邻两点进行内插,它的实现较为容易,因此这里不做进一步的解释。

图6 改进前后的闭环增益成形控制器的航向保持效果,目标航向为30°Fig.6 Course keeping control results of closed-loop gain shaping algorithm before and after improvement, desired course is 30°

图7 应用式(5)航向保持算法的航迹保持效果Fig.7 Trajectory tracking results applying course keeping algorithm in Eq.(5)

图8 应用改进航向保持算法的航迹保持效果Fig.8 Trajectory tracking results applying improved course keeping algorithm
表1为算法改进前后性能指标(ec为航向误差,et为航迹误差)。分析图7~9和表1可以得到以下结论:1)所提出的控制方法可以较理想地实现船舶航迹保持控制,改进算法控制效果总体上优于改进前。2)分离型积分项的引入对航迹保持中稳态误差依然有显著的消除效果。3)对执行器输出的非线性处理平缓和减小了舵角输出,但在大角度转向时存在增大航迹误差和超调的风险。4)航迹误差的衰减总是落后于航向误差。当然无论使用何种控制这种落后都是正常的,漂移的过程一定是航向领先,因此间接式控制是否增大了这一落后的时间尚难以界定。
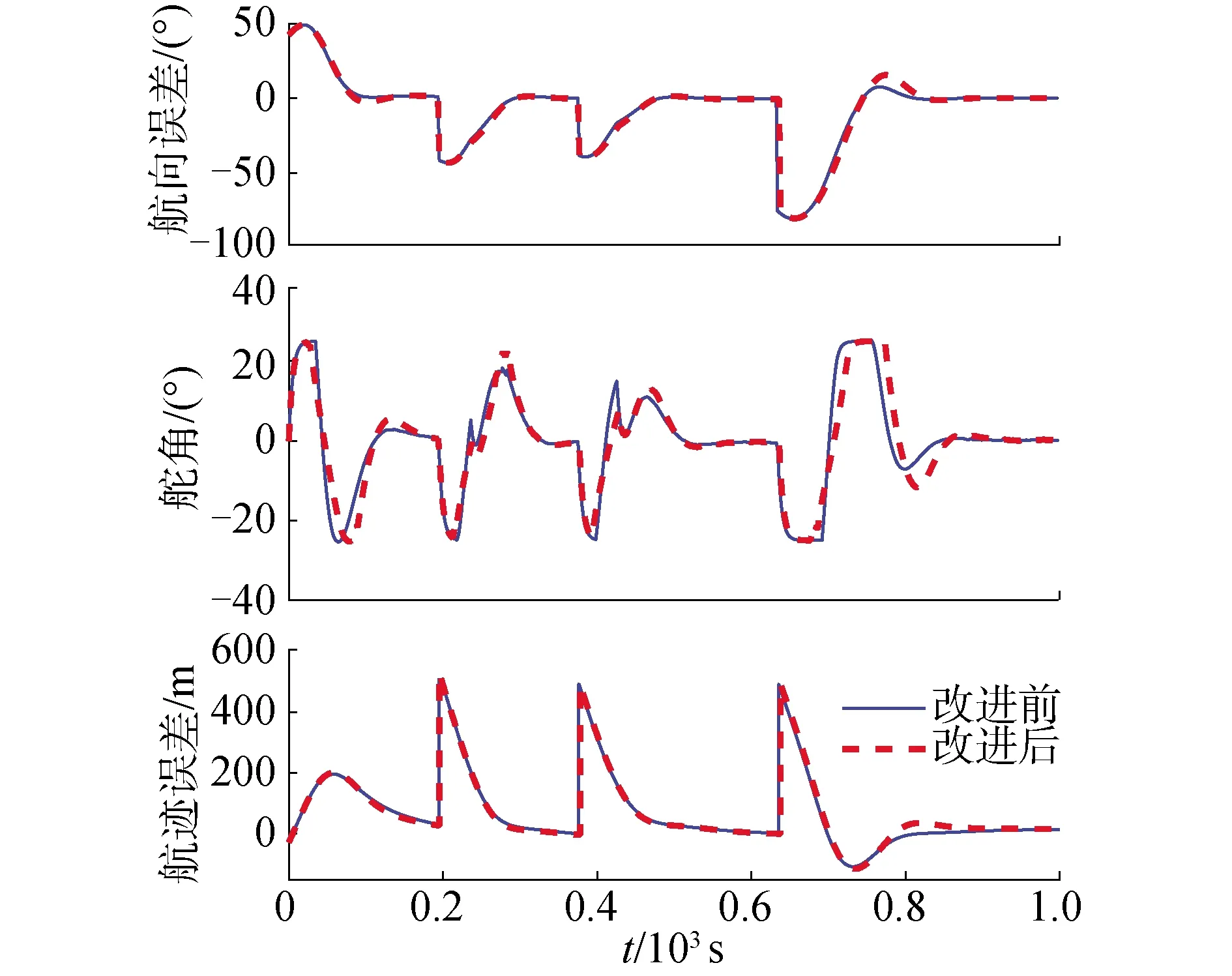
图9 改进前后的航向误差、舵角、航迹误差随时间的变化Fig.9 Course error, rudder angle, and deviation with time before and after improvement

表1 算法改进前后性能指标
4 结论
1)本文所采用的基于闭环增益成形算法的carrot following航迹保持策略可以实现航迹保持功能,效果令人满意。
2)由于是间接式控制,对于航向保持的既有技术也可以迁移到航迹保持的框架内,这些技术能够或多或少地保留原有的作用,发挥期望的效果。
3)就仿真结果而言,若转向角度小于90°,在转向点改变时能在90 s左右将航迹误差减小到20 m以内,若转向距离大于90°,则航向误差可能会有一定的超调,因此不建议在设计航路点时预设大角度转向。
4)在6级风的仿真条件下,航迹保持算法的稳态误差小于5 m,满足实际航海的要求。
若要加快航迹误差的衰减速度,可以尝试在控制率中引入航迹误差,或者结合文献[15]中的方法直接考虑操舵对船宽方向上动态的影响。对于大角度转向的超调问题,也可设计算法提前规划航迹以提前规避。
