光学腔中腔量子电动力学系统的理论成果

乔玉洁 张 罡

（ 天津师范大学物理与材料科学学院，天津300387）

1 概述

光学作为一门最基础的物理学科，在物理学的发展过程中起到至关重要的作用。但随着研究的深入，物理学家们发现经典力学已经不足以描述微观系统，所以在20 世纪初由普朗克、玻尔、海森堡、薛定谔等一大批物理学家共同创立的量子力学带领大家进入了“新世界”，至此一些经典力学中无法克服的困难——波粒二象性、黑体辐射、光电效应等都得到了合理地解释，量子力学的快速发展推动了科学技术的进步，也促进了我们对光的性质的进一步研究与探索。当我们将量子场论与光学相结合，用量子力学的观点处理光与物质的相互作用时，量子光学的概念就此提出。腔量子电动力学作为量子光学的一个主要的领域，在过去几十年中取得了巨大的进展，在量子信息和量子计算方面也体现出了极大的应用潜力。

2 腔量子电动力学简介

腔量子电动力学概念的首次提出可以追溯到20 世纪40 年代，1946 年Edward M. Purcell 在美国物理学春季会议上的论文摘要中提到[2]：当自旋系统与共振电路耦合时，原子的射频跃迁的自发辐射率会发生变化，这就打破了在这之前人们普遍认为自发辐射是一种固有属性的说法，从而使更多的科学家们把注意力放在自发辐射和能级移动方面。1948 年，Casimir 和Polder逐渐把单个原子与导电平面之间的研究扩展到两个平行金属板之间的相互作用情况[3，4]，并发现了“Casimir 效应”。20 世纪50年代，微波激射器[5]的实现激发了人们对腔中物质与辐射场相互作用的深入研究，在这段时期内，电子自旋跃迁自发辐射率的修正被预测并得到实验证实[6]。1963 年，Jaynes 和Cummings建立了一个理想模型“Jaynes Cumming（J-C）模型”，该模型的提出在腔量子电动力学的发展过程中具有里程碑的意义。1970年，Drexhage 等人第一次在实验中观察到“Purcell 效应”[7]。以上大部分实验都是在弱耦合条件下进行的，但随着科学技术的发展，腔QED 系统实验逐渐进入强耦合区域，在此区域可以使光子与原子的量子态更具有确定性，并且它们之间的相互作用也会增强，有利于促进量子态的传输，给量子信息的实现奠定了坚实的基础。

3 光频区段腔QED 的理论计算

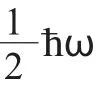
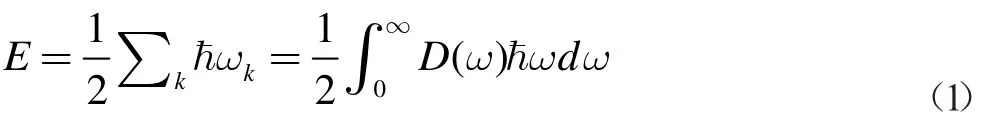
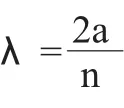
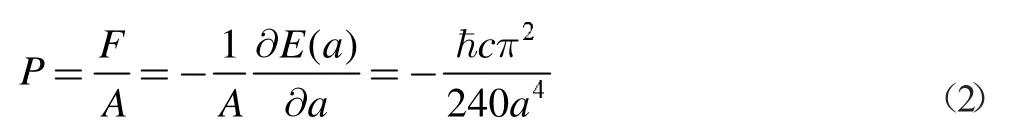
这是一个吸引力。我们把这种由外界其他波促使导体板产生吸引力的现象称为Casimir 效应，（2）式的Casimir 效应是非常微弱的，直到1996 年，物理学家首次对它进行了测定，使得理论值和实验值基本吻合。

然而在真实的光学腔中，腔内的电磁波会发生泄漏进而衰减，使得真实的光学腔存在耗散的问题，所以态密度不是一个理想的δ 函数。对于品质因素为Q 的光学腔，若我们只考虑腔模频率为v 时，由于腔模频率是基频的整数倍，高阶模式不容易被激发，所以可以采用单模近似的方法得到品质因素为Q 的光学腔与腔外电磁场耦合所致的谱密度为：

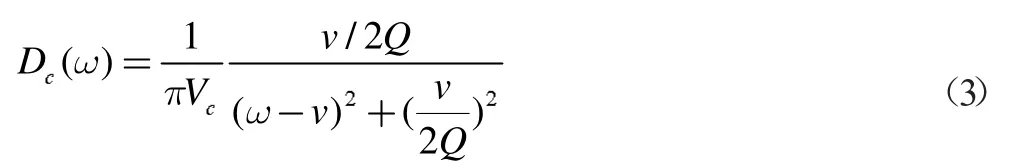
其中Vc是腔体积。

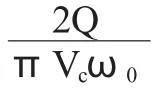
如果腔体积Vc～λ03，则自发辐射率有～Q 倍的提升。到目前为止，光学腔中自发辐射的抑制和增强均已经被实验所证实[10-12]。

接下来我们会从微观的角度对（3）式进行解释。对于一个非理想的光学腔来说，品质因素是由系统的微观参数决定的。非理想光学腔作为一个开放系统，光子可以在腔内部和外部之间隧穿，系统的哈密顿量为[13，14]：

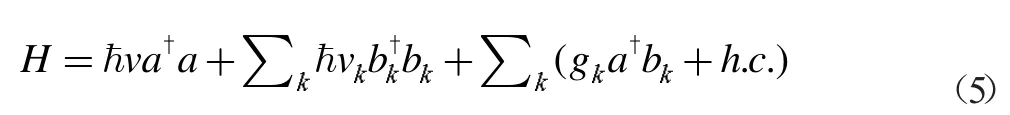
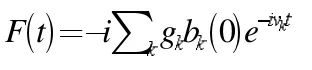
对其求解可得：

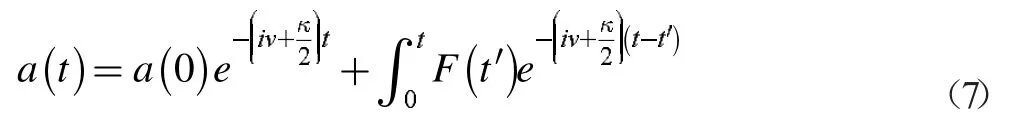
由于外部空间中的电磁场处于热平衡态，所以＜F（t）＞=0，可得：

由上式我们可以看出，腔内电磁场是以κ/2 的速率进行衰减，有品质因素Q=v/κ。则可以得到（7）式的关联函数：

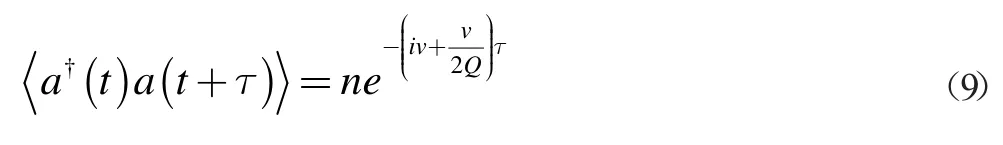
所以谱函数是

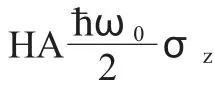
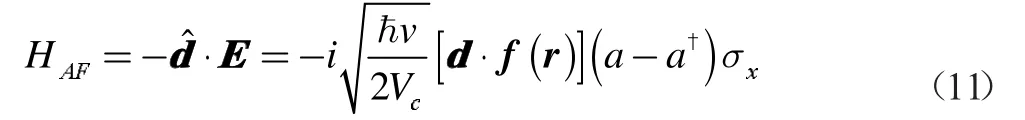
其中f（r）是光学腔中的驻波模式。

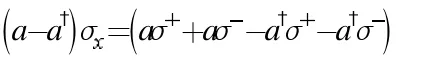
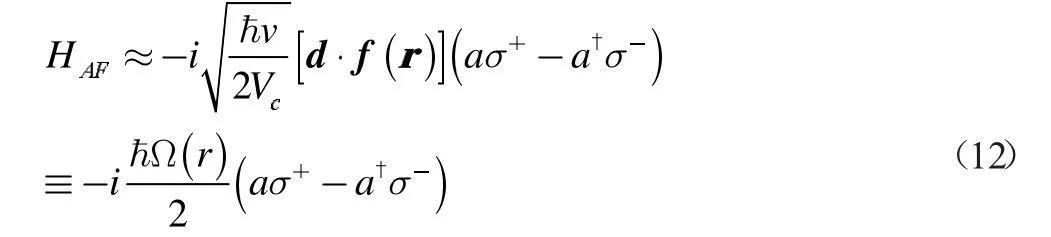
因此当腔内存在一个二能级原子时，总的哈密顿量是：

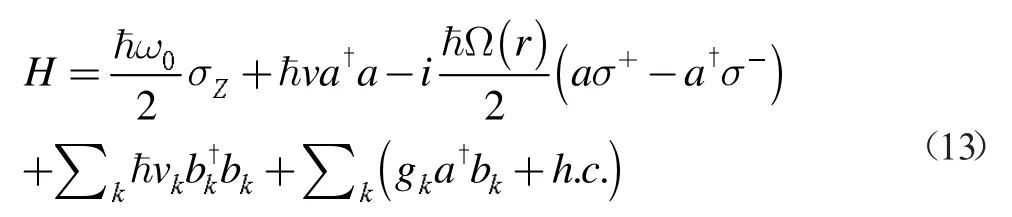
然后对光场（腔内和腔外）进行对角化，得到一系列简正模式，之后采用Weisskopf-Wigner 近似来处理原子的自发辐射，这种方法适用于 g （r ）≪κ的弱耦合区域。下面我们对其做简要描述：

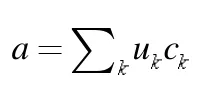
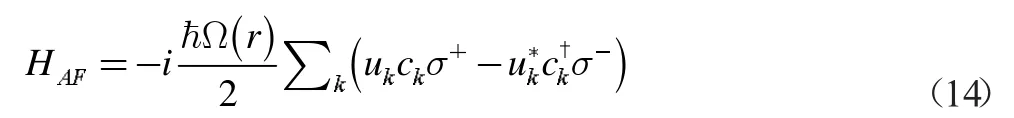
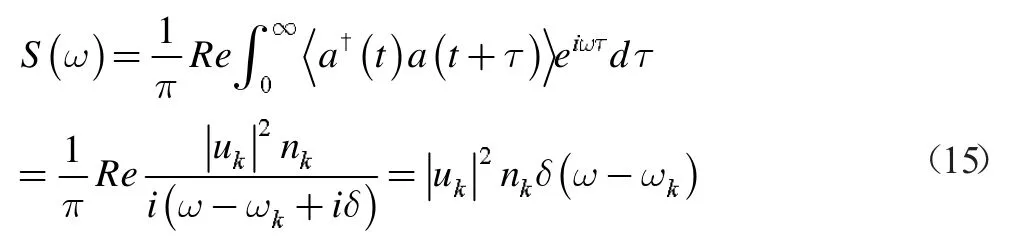
其中

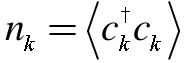
对于处理二能级原子的总哈密顿量（13）式，我们还有另一种方法，就是把原子和腔场视为一个系统，再考虑外部环境对其的影响，则系统密度矩阵的演化可以用主方程描述为[15]：

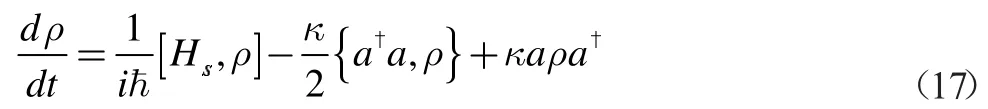
其中

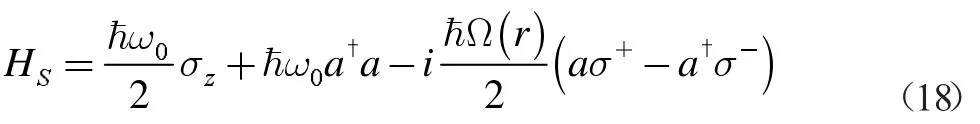
该方程描述的是原子和腔场的哈密顿量（这里已假定原子跃迁频率和腔模频率相等）。等式的第一项描述的是密度矩阵的幺正演化，第二项则是外部电磁环境导致的耗散。

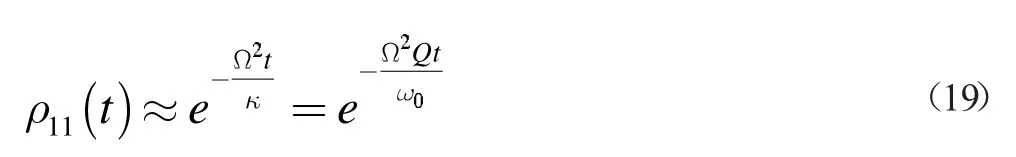
这一形式和真空中自发辐射类似，只不过衰变率改变了，这正是一开始得到的结论[2]。

另一方面，在Ω＞＞κ 的强耦合区，有：

因此当时间t＜＜1/κ 时，ρ11（t）呈现周期性的拉比振荡。这一结果定性上很容易理解，对于κ=0 的完美光学腔，激发态的原子辐射出的光子在腔中来回反射，原子- 光子耦合系统必然呈现拉比振荡；对于非理想光学腔，如果g＞＞κ，则在一个振荡周期内腔场几乎不衰减，那么也近似为拉比振荡。

4 Jaynes-Cummings 模型

Jaynes-Cummings 模型是由Jaynes 和Cummings 在讨论微波激射器（Maser）时提出的，它可以用来描述一个二能级原子与单模腔之间的相互作用，并且在旋波近似下，该原子- 腔耦合系统可以用Jaynes-Cummings 哈密顿量来描述[16]，其解析解也是较为容易得到的，还有利于进行动力学性质的研究。

目前为止，该模型已成功应用于一系列实验现象，如量子Rabi 振荡[17]等。

对于上面的（13）式，若我们只考虑系统的短期行为，忽略腔场的衰减，在不限制腔模频率等于原子跃迁频率的条件下，则由哈密顿量

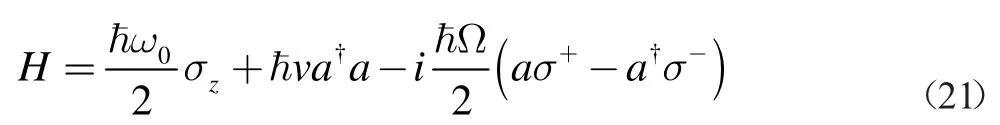
决定的幺正演化，就可以称为Jaynes-Cummings 模型[16]。

对H 做一幺正变化使其变为不含虚数的形式：

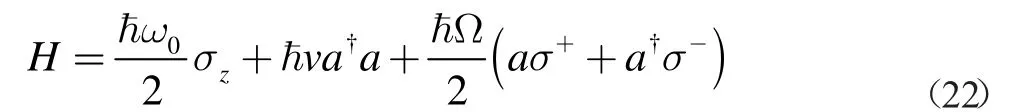
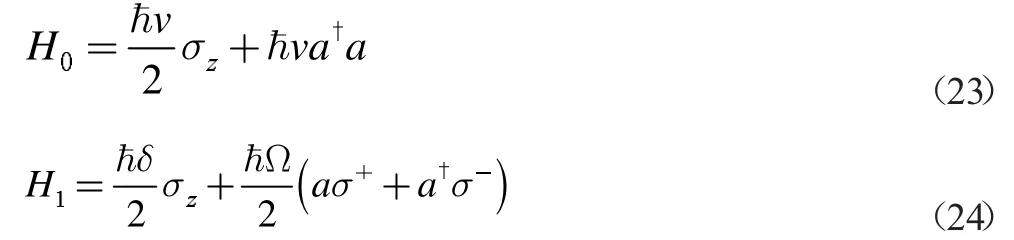
本征态为

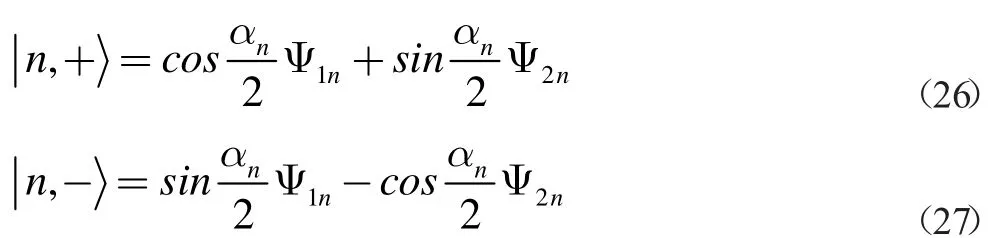
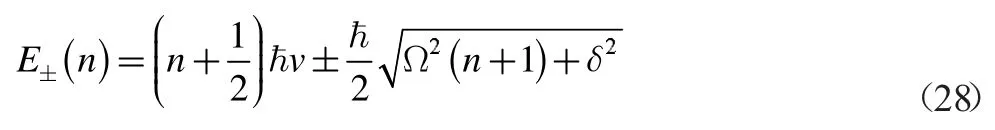
值得注意的是基态是特殊的，基态n=-1，只有一个态就是

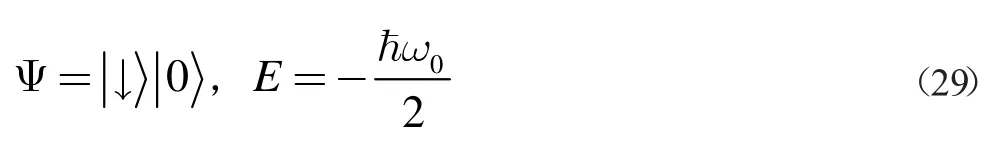
形如|n，±＞的态被称为“缀饰态”[18]，形象地说似乎是电磁场“装饰”了原子态。在失谐量δ=0 的情形，缀饰态的形式特别简单[19]：

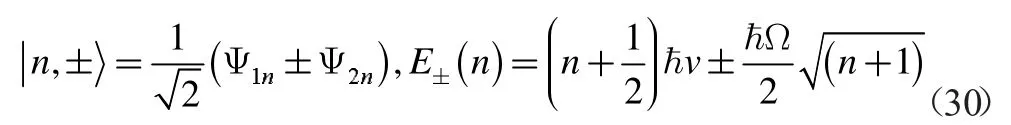
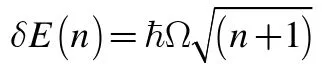
不同的是，二能级原子的Rabi 振荡是可以由半经典理论解释[20]。

5 结论

腔量子电动力学作为研究腔内原子与光场相互作用的系统，在量子理论方面展现出较好的应用前景，尤其在强耦合机制下的光频区，吸引了众多研究者的目光。CQED 的进展，对量子信息和量子计算的实现有着至关重要的作用。

本文给出了非理想光学腔下品质因素为Q 的光学腔与腔外电磁场耦合，所致的谱密度在微观角度的理论推导，以及给出的二能级原子与单模腔相互作用的理论计算，在后面的研究过程中，可以将其推广应用到多能级原子与单模腔相互作用动力学性质研究之上，以及对超强耦合机制方面的研究提供了理论基础。