一种基于多模型融合的电驱动车辆车速估计方法*

张 征，马晓军，张运银，陈路明

（陆军装甲兵学院兵器与控制系，北京 100072）

0 引言

纵向车速是车辆操纵稳定性控制研究的一个非常重要的状态信息，车速估计精度能够影响动力学控制的效果［1］。目前大多数车辆的车速信息是通过普通车载传感器信号计算处理得到的。对于非全轮驱动车辆，一般情况下可以将非驱动轮轮速传感器信号进行还原来估计车速，但是这种方法并不适用于全轮驱动车辆［2］。针对全轮驱动车辆，有学者应用非线性状态观测器估计纵向车速，这类算法一般需要构建非线性车辆模型和动态轮胎模型，完成非线性迭代计算，计算量较大并且实时性难以保证［3-4］。文献［5］提出了基于车身纵向加速度积分的车速估计方法，但这种方法因为长时间积分容易引起信号噪声误差持续累加等问题，严重影响估计精度。另外，还有一些研究者采用卡尔曼滤波、粒子滤波等算法对纵向车速进行估计，这些算法适用于驱动轮没有发生过度打滑的工况，当路面情况不佳时，滤波算法估计精度容易受到影响［6-7］。

鉴于轮毂电机驱动车辆车速估计存在很大困难，本文提出了一种基于多模型融合的车速估计方法。根据采集的车载传感器信号和电机反馈信息，设计了自适应卡尔曼滤波车速估计器，同时采用车身加速度积分对车速进行估计，并结合车辆行驶工况和路面条件，将两种模型进行加权融合，提高了车速估计算法在各类行驶工况下的准确性和鲁棒性。最后，采用基于dSPACE 的实时仿真平台进行了仿真实验。

1 车速估计结构及原理

为轮毂电机车辆设计一种基于多模型融合的纵向车速估计方法，如图1 所示。

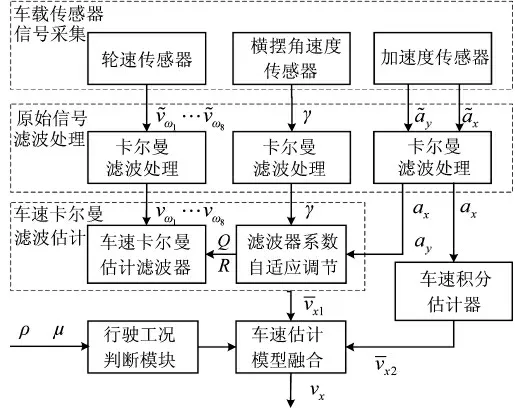
图1 基于多模型融合的车速估计器

2 自适应卡尔曼滤波器设计

2.1 车速估计卡尔曼滤波算法

考虑车辆大部分行驶工况都是在作平面运动，因此，依据线性二自由度车辆模型设计卡尔曼滤波器。将纵向车速视为均匀变化信号，取经滤波处理后的各轮轮速平均值作为量测量，得到车速估计系统状态空间模型为

示加速度的过程噪声。

2.2 滤波器系数自适应调节

假设所设计的车速卡尔曼滤波估计系统的过程噪声均值等于0 并且服从高斯分布，过程噪声协方差矩阵可表示为

而后，按照如图2 所示步骤进行车速自适应卡尔曼滤波估计。

图2 自适应卡尔曼滤波算法框图

3 多模型融合方法设计

3.1 基于加速度积分的车速估计算法

当车辆在低附着路面行驶或车速较高时，车轮容易打滑，此时车轮速度与车速的关联性减小，应用卡尔曼滤波算法计算出的车速估计精度将难以保证。这种情况下需要结合纵向加速度积分方法进行车速估计，车速与纵向加速之间关系可以近似表示为

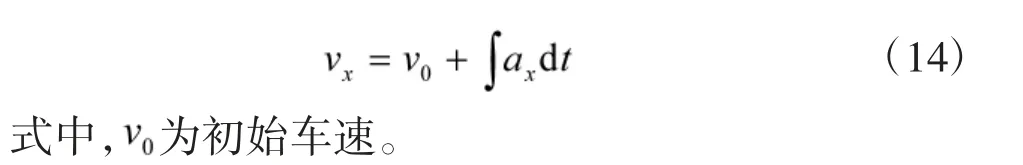
3.2 车速估计模型融合方法

对轮毂电机驱动车辆进行车速估计时，由于卡尔曼滤波和加速度积分两种算法在各类行驶工况下的估计效果不同，仅采用单一车速估计模型难以满足车辆全工况的状态参数估计需求，因此，将两种估计模型进行融合，通过最小方差加权平均法得到车速估计值，其基本思路如下：

根据路面附着条件（路面附着系数μ）和加速/制动踏板开度（ρ）对车辆行驶工况进行划分，行驶工况Apq（p=1，2，3 且q=1，2，3）的具体判断方法如下页表1 所示。

表1 行驶工况判断

4 仿真结果及分析

为了验证所提出方法在不同行驶工况中的车速估计效果，利用基于dSPACE 的实时仿真实验平台开展实验。

实时仿真实验平台由驾驶员操控舱，dSPACE综合控制系统，基于RT-LAB 的电机驱动系统，基于RT-LAB 的综合电力系统，和基于Vortex 软件的动力学仿真系统构成，各系统间采用Flexray 总线通信。平台具体结构如图3 所示。

为了验证所提出方法在不同行驶工况下的车速估计效果，设计4 种行驶工况：在高附着路面（μ=0.8）进行轮毂电机驱动车辆直线加速和低速小半径转向仿真；在低附着路面（μ=0.3）分别进行急加速行驶和紧急制动仿真，具体实验条件设置如表2所示。其中方向盘转角满程为900°，油门踏板ρA∈［0，1］，制动踏板ρB∈［0，-1］。

图4～图7 分别为4 种工况下的驱动轮轮边速度信号、估计车速和仿真车速比较结果，表3 为车速估计误差统计结果。

图3 硬件在环实时仿真平台

表2 车速估计实验条件设置

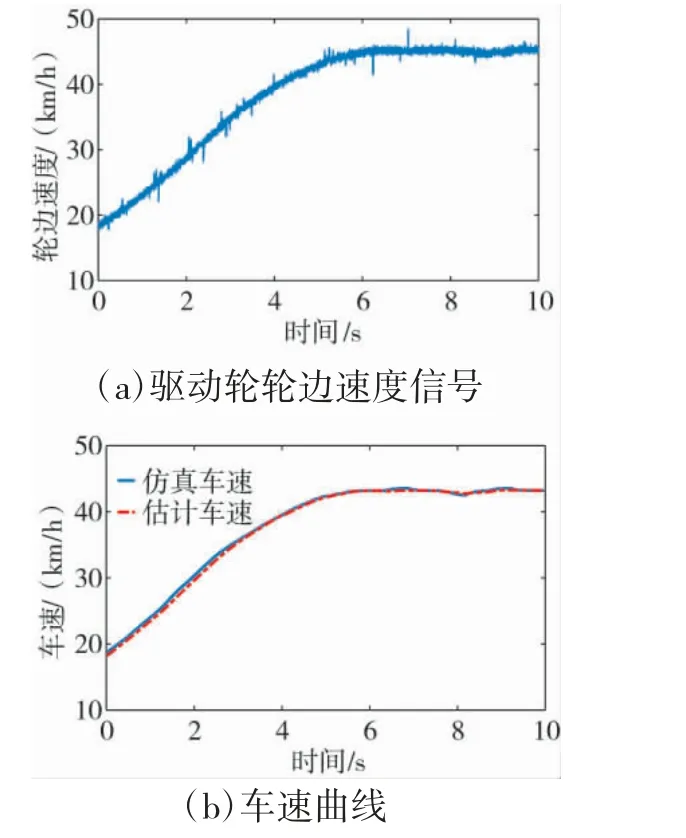
图4 直线加速工况

由图4 和下页图5 可知，当车辆在高附着路面正常行驶时，驱动轮打滑情况不严重，轮边速度信号未出现较大波动。无论是在直线行驶还是转向工况下，采用多模型融合车速估计器都能够观测出较为准确的纵向车速信息。

从图6 和图7 实验结果可以看出，在低附着路面行驶时，一旦采取急加速或紧急制动，车轮将容易发生严重滑转/滑移。在强驱动行驶工况下，起步阶段轮边速度信号出现较大跳变；在强制动工况下，轮速信号也发生了很大波动。但多模型融合车速估计方法仍然保证了过度打滑情况下的估计精度，估计车速与仿真车速误差得到了很好的控制。

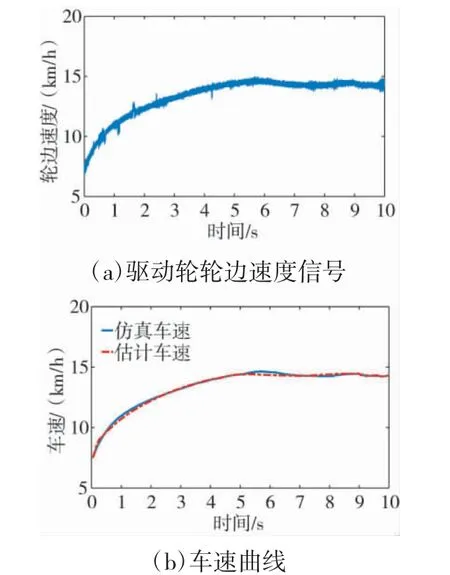
图5 低速小半径转向工况

图6 急加速行驶工况

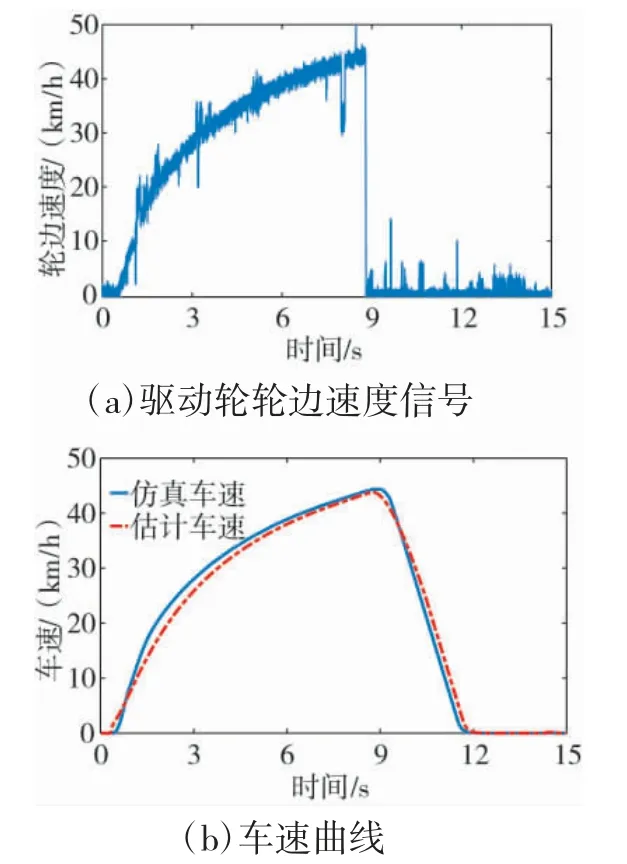
图7 紧急制动工况

根据表2 所示，车速估计误差统计结果可以看出，估计车速与仿真车速间最大误差都能控制在2 km/h 以内，并且均方误差都很小，这就验证了多模型融合车速估计方法在车辆不同行驶工况下都有良好的车速估计效果。

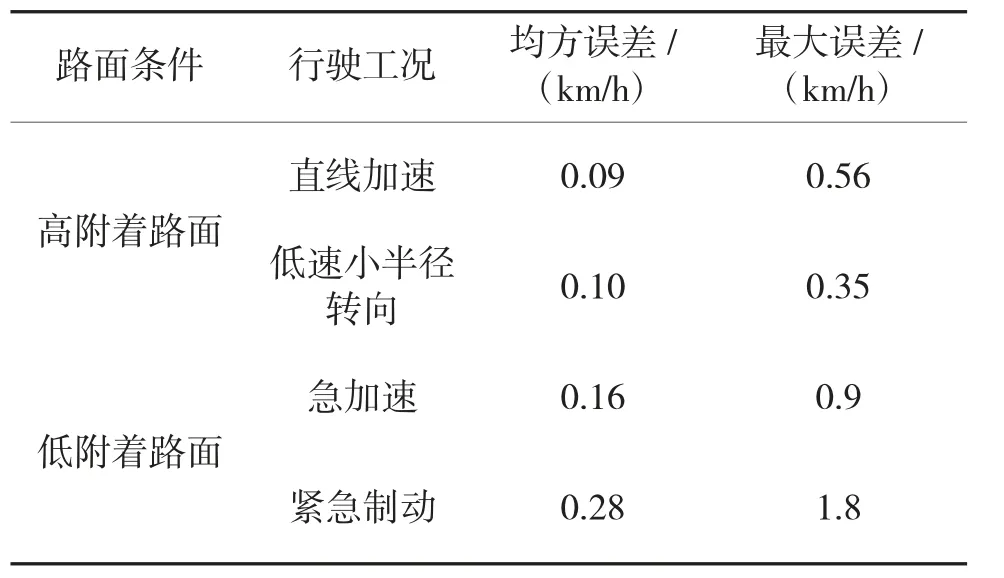
表3 车速估计误差表

5 结论

本文将某型88 轮毂电机驱动车辆作为研究对象，设计了一种基于自适应卡尔曼滤波和信号积分数据融合的车速估计方法。在建立线性二自由度车辆模型的基础上，运用卡尔曼滤波算法设计了车速估计器，并进行滤波系数的自适应调节。同时又采用了信号积分法估计车速，通过最小方差加权平均法将两种估计模型进行了数据融合，得出最终车辆行驶时的车速估计结果。采用dSPACE 实时仿真平台，设计并完成了多种行驶工况的车辆操纵实验，仿真结果表明，所提出的多模型融合方法有效改善了单一状态参数估计方法适用范围局限，易受干扰等问题，在不同工况下都具备良好的估计效果。