非确知先验信息条件下MIMO 雷达波形设计*

姚 遥，周吉生，李 琼，王洪雁

（1.周口师范学院物理与电信工程学院，河南 周口 466000；2.周口科技职业学院汽车工程系，河南 周口 466000；3.周口市农业科学院，河南 周口 466000；4.大连大学信息工程学院，辽宁 大连 116622）

0 引言

相较于传统相控阵仅可发射相干信号，多输入多输出（Multiple-Input Multiple-Output，MIMO）雷达可同时发射互不相关波形，并在接收端对所有回波联合处理以获得目标检测及参数估计结果［1-2］，MIMO 雷达可提升干扰相消能力，增强参数辨识性和发射方向图设计的灵活性［3］。此外，具有较高设计灵活性，以及较低截获概率的正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）技术在雷达领域受到了众多研究人员的关注［4］。

由林肯实验室提出的空时自适应处理（Space-Time Adaptive Processing，STAP）方法可抑制地、海面杂波，因而显著提升复杂场景下慢速目标的检测性能［5］。麻省理工学院的Bliss 等将STAP 方法引入MIMO 雷达体制，并考虑了波形设计问题［6］。Sen 则在OFDM 雷达平台上结合STAP 技术及目标空域稀疏性以提升目标检测概率［7］。由上述文献可知，可综合利用MIMO 及OFDM 优势以改善STAP检测性能，文献［8］已对此问题作了初步研究。

为改善MIMO 雷达检测及估计性能，众多研究人员对波形设计进行了深入探索。基于克拉美罗界（Cramer-Rao bound，CRB），文献［9］提出改善参数估计精度的波形设计方法，而文献［10］则考虑联合优化波形相关矩阵（Waveform Covariance Matrix，WCM）及接收权，以提高参数估计性能。Wang 等通过设计WCM 以最大化输出信干噪比（Signal to Interference and Noise Ratio，SINR）进而提升目标检测概率［11］。应该指出，上述有关波形设计问题的求解需要有关环境或目标参数的确切值。实际应用中，这些参数值须通过估计得到，因而存在不确定性，而基于存在估计误差的参数估计值所得最优波形将使得雷达检测或估计性能下降［9，11］。

针对上述问题，考虑将目标参数不确定性包含进波形设计问题，基于极大极小方法，本文构建了稳健波形设计问题，以降低STAP 检测性能对目标参数估计误差的敏感性。由于检测概率与发射波形的函数关系比较难以解析表示，因而本文基于最大化输出SINR 准则［11］，在目标参数不确定性及发射波形相关物理约束下，最大化最差条件下MIMO-OFDM-STAP 输出SINR 以改善目标检测的稳健性。为求解所得NP-hard 问题，先将OFDM 信号恒模约束等价为低峰均比（Peak-Average-Ratio，PAR）约束，然后利用对角加载（Diagonal Loading，DL）［12］将其重构为可有效求解的半定规划（Semidefinite Programming，SDP）问题［13］。

1 问题描述

文中采用如下配置的共置MIMO 雷达：发收器为分别具有M，N 个阵元、阵元间距为dT、dR的均匀线性阵列。高度为h 的雷达载体以速度v 沿阵列方向运动，目标则以vt与载体相向而动。脉冲重复周期（pulse repetition interval，PRI）T 内，发射阵列中任一阵元发射某个OFDM 子带信号。则第n 个阵元在第l 个PRI 内接收信号可表述如下：

式中，Cm为第m 个发射波形幅度，P 为发射功率。

2 基于DL 的联合优化问题求解

由于式（24）第2 项约束为恒模约束，因此，NP-hard 问题［13］，非常难以求解［12］。为求解此问题，此处须首先考虑波形恒模特性。由于具有有限符号的恒模波形无法满足设计需求［16］，因而，可利用低PAR 近似恒模约束［17］，即：

3 仿真结果及分析

ASNR 及CNR 皆为30 dB，本文方法所得波束方向图如图1 所示。明显地，目标附近，波束方向图具有较大增益，表明发射阵列将主要功率聚焦于较小输出SINR 所在位置，以提升最差条件下MIMO雷达检测性能。此外，观察到图1（b）出现栅瓣，这是由于雷达B 发射阵元间距较大所引起［9］。

图1 ASNR=CNR=30 dB，本文算法所得波束方向图

为检验最差条件下检测性能的提升，下页图2示出所提算法，不相关信号和目标信息确知条件下非稳健方法所得最差条件下输出SINR 随ASNR 或CNR 变化。由图2 可得，由本文方法，非稳健算法以及非相关信号所得SINR 与ASNR 变换趋势相同，与CNR 则相反。再者，无论何种条件下，所提算法所得SINR 皆高于非相关信号，且所提算法与非稳健算法所得SINR 差距较小，因而本文算法可显著提升最差条件下检测概率。此外，由图2（a）、（b）可得，雷达B 所得SINR 大于雷达A，这是因为雷达B 所形成虚拟孔径大于雷达A［9］。

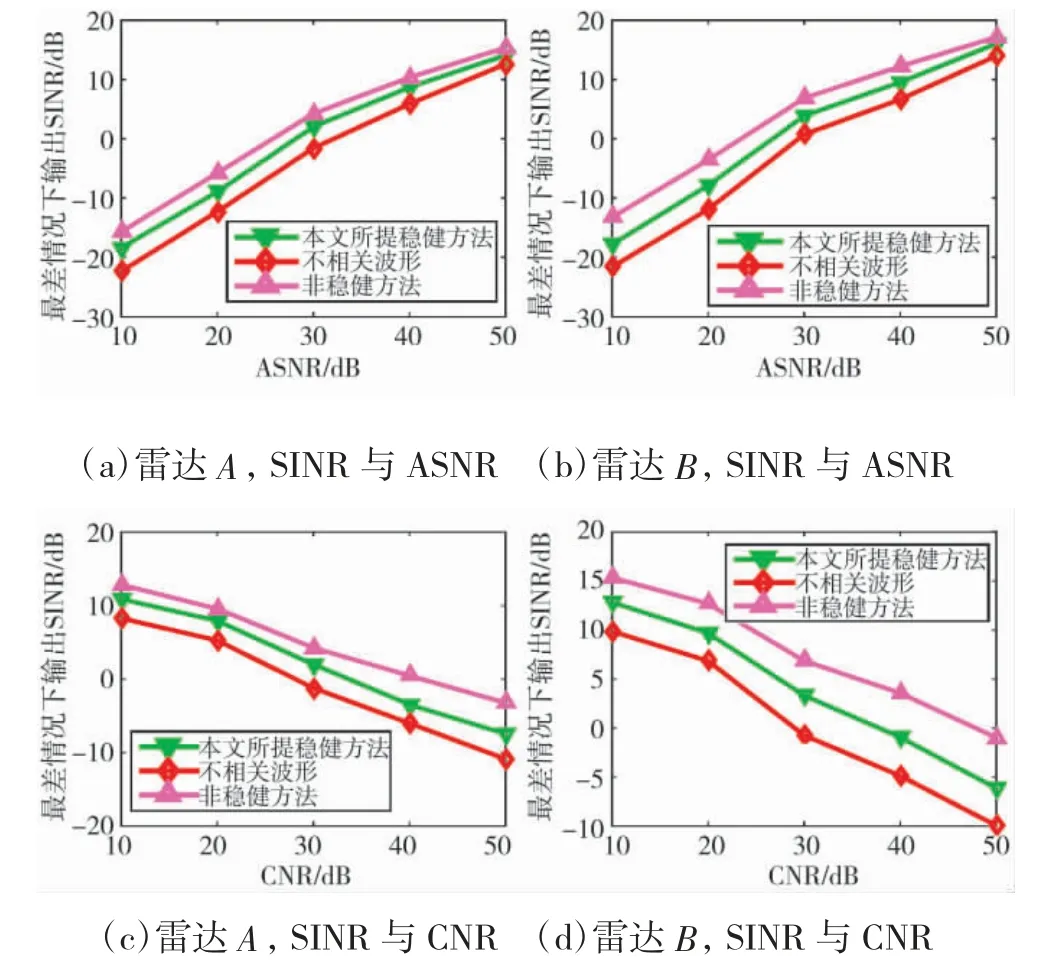
图2 ASNR=30dB 或CNR=30dB，本文算法，目标信息确知场景下非稳健方法和不相关信号所得最差条件下输出SINR 随ASNR 或CNR 变化

上述3 种方法所得平均最差条件下输出SINR随ASNR 或CNR 变化趋势如图3 所示。由图3 可得，与其余两种方法相比，所提算法具有较高平均最差情况下输出SINR，即所提算法具有较好的稳健性。

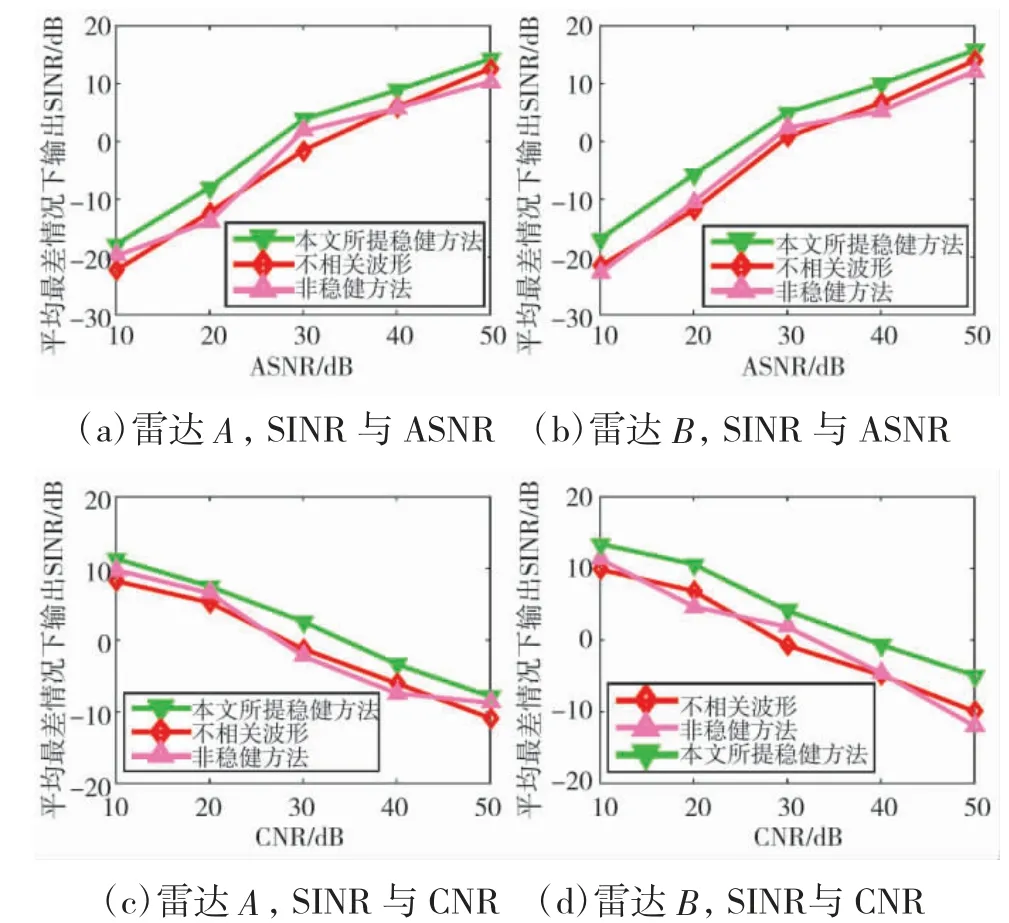
图3 ASNR=30 dB 或CNR=30 dB，3 种方法获得平均最差条件下输出SINR 随ASNR 或CNR 变化

为检验峰均比约束上界对输出SINR 的影响，ASNR 及CNR 皆为30 dB 条件下，图4 所示出上述3 种算法所得最差条件下输出SINR 随峰均比约束上界变化曲线。由图4 可知，3 种算法所得输出SINR 皆随峰均比约束上界增加而增大，且当峰均比约束上界增加至一定值后，所得输出SINR 不再随其变化而变化。此外，无论峰均比约束上界取何值，所提算法所得最差条件下输出SINR 皆优于其他两种方法。

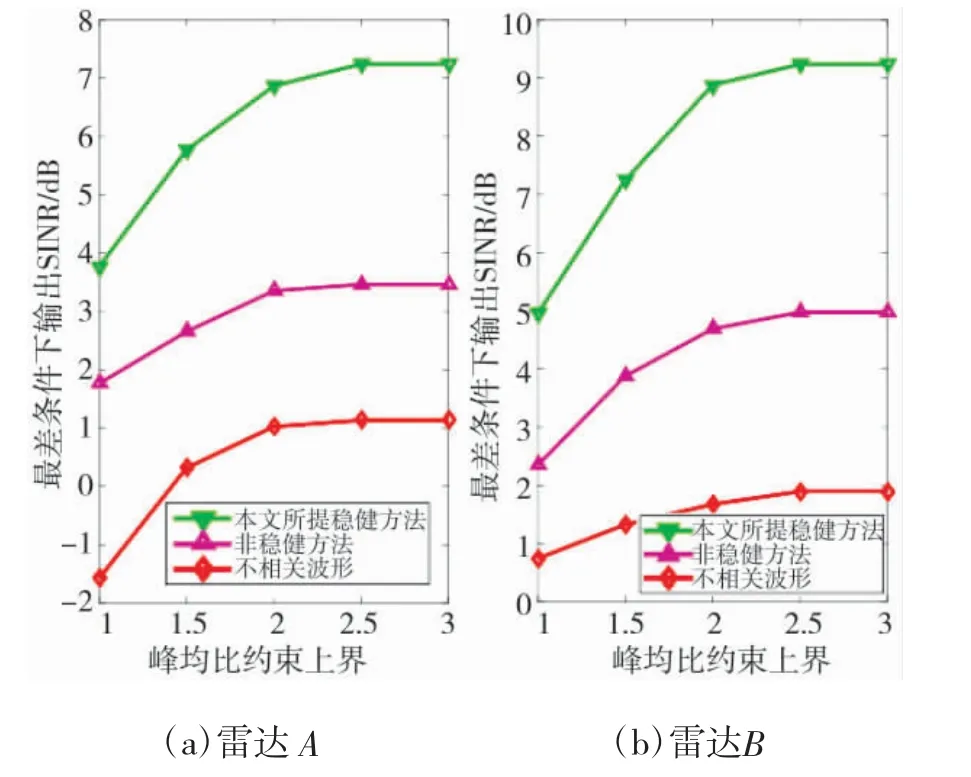
图4 ASNR=CNR=30dB，最差情况下输出SINR 随峰均比约束上界变化

图5 ASNR=CNR=30 dB，最差情况下输出SINR随DL 因子与WCM 最大特征值比值变化

4 结论

基于最大最小准则，在发射功率、目标不确定凸集及峰均比约束下，本文研究了目标导向矢量存在估计误差条件下，波形优化问题以提升基于MIMO-OFDM 雷达的STAP 检测概率的稳健性。为求解所得NP-hard 问题，本文基于对角加载方法在目标导向矢量不确定集合上设计发射波形。通过与非稳健方法及非相关发射信号在最差条件下，输出SINR 的提高以及稳健性的改善等方面的比较，仿真表明，本文所提方法可明显提升MIMO-OFDM-STAP检测概率对目标参数估计误差的稳健性。