空调压缩机低速无位置传感器控制策略

（江西理工大学电气工程与自动化学院，江西 赣州 341000）

空调压缩机由于内部含有高强度的腐蚀性制冷剂，无法安装位置传感器，常用I/f控制策略对IPMSM进行位置开环启动及低速运行，电机运行到中高速时，利用永磁同步电机的反电势估算转子的位置与转速信息[1]，常用的获取反电势方法有滑膜观测器[2]方法、模型参考自适应[3]方法、扩展卡尔滤波[4]方法。I/f控制方法存在低速无法进行位置闭环的缺点，易导致永磁同步电机运行过程中发生失步，无法实现大负载启动。

当电机运行在零速或低速条件下时，有用的反电势信号信噪比非常低，从而利用反电势获取转子位置与转速信息在电机零速与低速时失败。为了能够在低速甚至零速条件下获得转子位置的信息，高频信号注入法是解决该问题的一个有效方法[5]。其基本思想是把一个高频电压信号叠加到基波信号上，共同施加给永磁同步电机的三相绕组，相应的高频信号中含有转子位置信息，采用带通滤波器可以将基波信号滤出，通过信号解调，再经低通滤波就可以得到转子位置信息。目前，常用的高频注入信号主要包括旋转高频电压信号[6-8]和脉振高频电压信号[9-11]。目前，旋转高频电压信号和脉振高频电压信号两种磁极方向辨识算法执行时间长[12-13]，电机在运行时，将导致得到的转子位置滞后，且在实际应用中，由于采样精度与频率受限制，检测难度大。

为了克服上述方法的缺点，提出了一种新的判别磁极方向的方法，通过对高频模型下的直轴高频的正负半轴电流分别进行积分，根据积分值的大小判断出转子磁极方向。仿真与实验结果表明上述提出的方法简单可靠，易于实现。

1 脉振高频正弦电压激励下的三相PMSM的电流响应

图1为实际与估算的同步旋转坐标系示意图。

图1 实际与估算的同步旋转坐标系示意图Fig.1 The schematic of the actual and estimated synchronous rotating coordinate system

如图1所示，首先建立了以转子N极方向进行定向的实际的d-q坐标系，转子磁极位置N极方向与α-β坐标系的α轴之间角度为θs，θg为算法跟踪收敛得到的角度，dg-qg坐标系为以θg进行解耦定位的估算的旋转坐标系，记实际d-q坐标系与估算的dg-qg坐标系的角度差为Δθ=θs-θg。

当dg-qg坐标系的dg轴方向注入信号为ug=um·分配到实际的d-q坐标系的电压为

式中：um为注入电压信号的峰值；ωc为注入的正弦波频率。

由式（1）可以看出，当注入的正弦波频率ωc足够大，即感抗远大于阻抗时，可忽略电阻上的电压，电机转速为0时，实际的d-q坐标系的d轴与q轴电压可化简为

对式（2）右边的电流did，diq进行积分得到：

根据式（3）的d，q轴电流可得到合成的高频定子电流ic，即

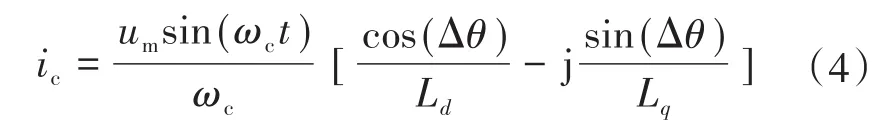
将式（4）转换变型为指数形式可得：

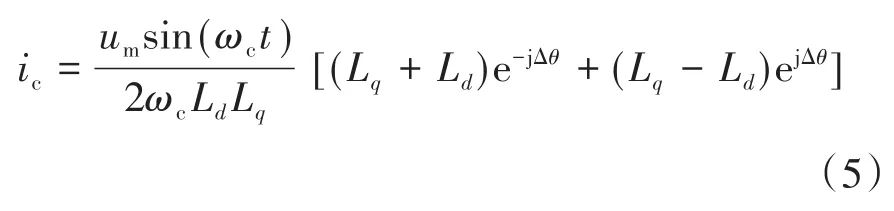
式中：Lq，Ld分别为q，d轴方向电感。

高频定子电流ic在dg-qg坐标系上的电流的表达式为

2 转子位置估算方法

2.1 利用Arctan函数的转子位置估算方法

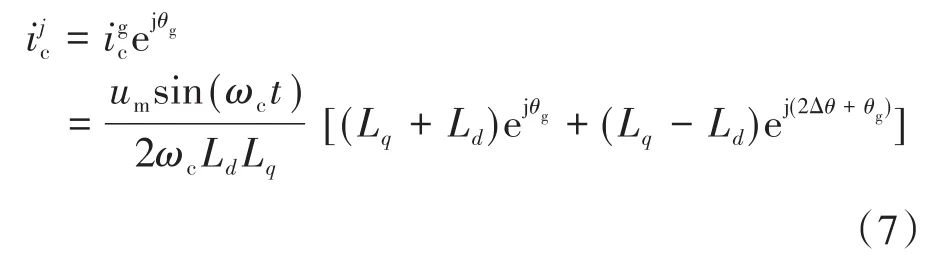
由式（8）可知，经过解调后的方程右边由两项组成：一项为关于估算偏差2Δθ的常量；另一项频率为注入电压信号频率的两倍的高频余弦信号。于是可通过一阶低通滤波器滤出高频余弦信号，得到关于估算偏差2Δθ的常量。对式（8）进行低通滤波后得到：

由式（9）可得到经过滤波后的α-β轴坐标系下的iα-LPF与iβ-LPF，即

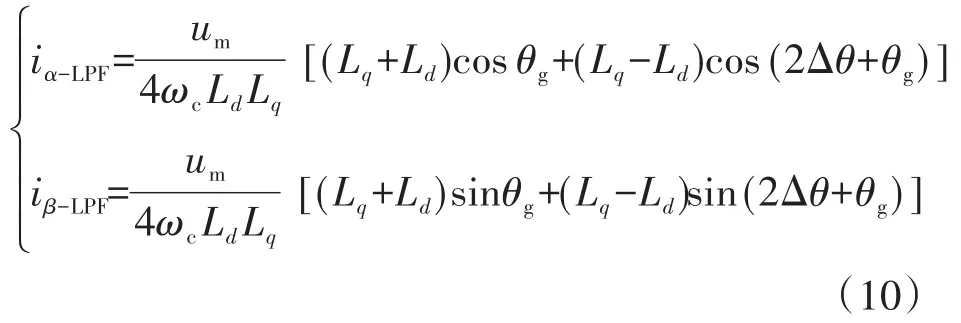
若给θg=0方向注入信号时，有：

若给θg=π/2 方向注入信号时，有：

由式（11）、式（12）得到：

对式（13）进行变型可得：

由式（14）可以看出，利用Arctan函数即可计算出永磁体的转子位置角度，即

其中

利用Arctan函数计算转子位置角度存在的缺点：该方法属于开环控制，受电流检测周期与精度的影响大，抗干扰性差，因而易受基波电流的影响，只适用于电机静止时的情况，具有局限性，且导致估算出的转子位置角度不平滑与高频抖动。

2.2 基于锁相环的转子位置估计方法

正如前文所述，鉴于利用Arctan函数计算转子位置的方法的局限性与缺点，提出了基于锁相环（PLL）获得转子位置的方法。图2为控制系统的结构原理图。图 2 中T-1（θg）为反 Park 变换；T（θg）为Park变换；SVPWM-VSI为逆变器驱动模块；T3s/2s为Clarke变换；LPF为低通滤波器。

图2 基于PLL获得转子位置角度的系统结构原理图Fig.2 Schematic diagram of the system structure for obtaining the position angle of permanent magnets based on PLL

由式（16）可知，q轴电流为幅值受估算偏差2Δθ的正弦值影响的正弦信号，且当2Δθ为0或的整数倍时，幅值为0。

对式（16）的dg-qg坐标系下的q轴电流作调解可得：

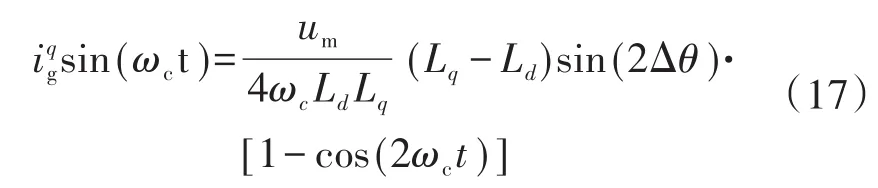
经过解调后的式（17）右边由两项组成：一项为关于估算偏差2Δθ的常量；另一项为频率为注入电压信号频率的两倍的高频余弦信号。可通过一阶低通滤波器滤出高频余弦信号，得到关于估算偏差2Δθ的常量。对式（17）的解调后的信号的进行低通滤波后得到：

当sin(2Δθ)足够小时，可认为2Δθ=sin（2Δθ），经过如图3所示的锁相环模块，即可收敛得到转子的位置与转速。

图3 锁相环模块Fig.3 Phase-locked loop module

根据图3可得到由θg到θs的传递函数G(s)，即

其中

式中：ξ为阻尼系数；ωn为角速度，决定PI调节器的带宽；Kp，Ki为PI调节器的参数。

当输入信号的角频率在0以上且ωn以下时，锁相环能快速地跟随输入信号的幅值与频率，否则跟随失败；ξ主要影响的是传递函数的动态性能，且ξ=1时，为临界阻尼状态。

3 转子磁极方向识别

目前常用的转子磁极方向识别有两种方法：一种是在估算得到的转子位置的正、反方向施加幅值相等、时间相同的电压，通过检测出两种情况下的直轴电流，电流峰值大的即为磁极正方向；另一种是在估算得到的转子位置正、反方向施加幅值相等、时间相同的电压，检测出两种情况下，直轴电流从稳态值衰减至0时所用的时间，时间较小的为磁极的正方向。上述两种方法有2个缺点：1）电流过零点时有震荡，易导致采样得到的结果存在误差；2）对采样电路要求高，抗干扰性差，增加了硬件成本；为克服以上缺点，提出了通过对高频模型下直轴高频的正、负半轴电流分别进行积分，并根据积分值的大小判断出转子磁极方向的方法。

当电机转子的初始位置在特殊位置时，即式（18）中sin（2Δθ）等于0时，Δθ=0，±π/2，π中仅当Δθ=0时，估算的转子位置与实际位置相同，当Δθ不等于0时，电机必然会启动失败，只有通过正确辨别出转子的极性，才能使电机顺利启动。

当Δθ=±π/2时，即估算的转子位置与实际的转子位置之间角度为90°，从而无法利用定子电流的非线性磁化识别转子极性。图4为特殊位置排除方法流程图，可避免Δθ=±π/2。

图4 特殊位置排除流程图Fig.4 Flowchart of special location exclusion

特殊位置排除方法具体实施步骤为：

1）设定初始高频注入角度为0；

2）采样得到的相电流经矢量变换得到q轴电流，q轴电流信号经调解与滤波得到f（Δθ）；

3）判断f（Δθ）是否为0，如果是0则跳转至步骤1），并改变初始高频注入角度a，a不等于0，±π/2，π之外的任意一个角度。否则执行步骤4）；

4）位置估算得到转子位置信息。即可开始进行转子极性识别。

式（16）中的d轴高频响应电流为

因f（Δθ）收敛 于 0，即 Δθ=0 或 π。 则 cos（2Δθ）=1，则估算同步旋转坐标系下的d轴高频电流响应可表示为

当f（Δθ）收敛于0时，估算得到的转子位置角度与实际的转子位置角度之差有两种情况：第一种为θg=θs；第二种为θg=θs+π。下面分别分析两种情况下估算同步旋转坐标系下的d轴高频电流响应。

情况1：θg=θs。当0＜ωct＜π时，相电流生成的磁链与转子的永磁体的N极方向一致，此时磁路产生饱和，d轴电感减小，d轴高频响应电流增大；当π＜ωct＜2π时，相电流生成的磁链与转子的永磁体的N极方向相反，此时磁路退出饱和，即d轴电感增大，d轴高频响应电流减小。dg-qg坐标系下的ig-d波形如图5所示。

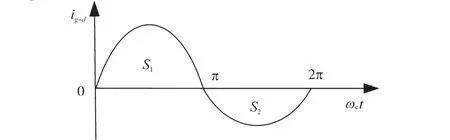
图5 θg=θs时的电流波形Fig.5 Current waveform when θg=θs

ig-d在区间[0 π]与区间[π 2π]分别与x轴围成的面积为S1，S2，且S1＞S2，其中S1，S2为

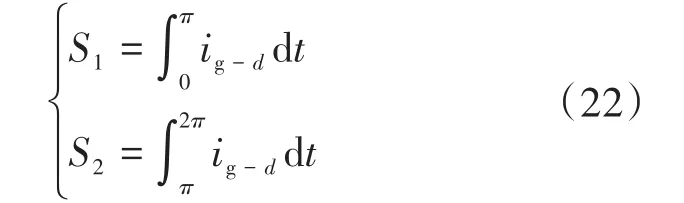
根据式（22）对正、负半轴的d轴高频响应电流分别积分，当S1＞S2时，则θg=θs，即可识别转子极性。

情况2：θg=θs+π。当π＜ωct＜2π时，相电流生成的磁链与转子的永磁体的N极方向一致，此时磁路产生饱和，导致d轴电感减小，d轴高频响应电流增大；当0＜ωct＜π时，相电流生成的磁链与转子的永磁体的N极方向相反，此时磁路退出饱和，即d轴电感增大，d轴高频响应电流减小。估计同步旋转坐标系下的ig-d波形如图6所示。ig-d在区间[0 π]与区间[π 2π]分别与x轴围成的面积为S1，S2，且S1＜S2，即当S1＜S2，θg=θs+π。

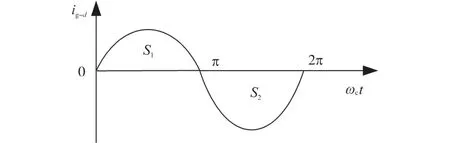
图6 θg=θs+π时的ig-d电流波形Fig.6 ig-dcurrent waveform when θg=θs+π

4 仿真与实验结果分析

4.1 仿真结果分析

通过Matlab/Sinmulink搭建仿真模型，设定仿真参数为：电机三相内置式永磁同步电机，电阻R=0.025 25 Ω，交轴电感Lq=0.001 09 H，直轴电感Ld=0.000 573 H，极对数p=6；三相逆变器端电压为48 V，开关频率为10 kHz。注入的高频电压信号幅值为5 V，频率为1 kHz，初始注入角度为0。为了验证改进后的转子位置估算方法的实用性与抗干扰性，在仿真过程中，电机启动时，给定速度为 100 r/min，在 0.2 s时突加负载 10 N·m，在0.5 s时突然给定速度为-100 r/min，图7为利用Arctan函数的转子位置估算方法得到的转子位置图，图8为利用Arctan函数的转子位置估算方法得到的位置估算误差图，图9为基于锁相环的位置估算方法得到的转子位置图，图10为基于锁相环的转子位置估算误差图。

图7 利用Arctan函数的转子位置估算方法得到的转子位置Fig.7 Rotor position obtained by the rotor position estimation method with Arctan function

图8 利用Arctan函数的转子位置估算方法得到的位置估算误差Fig.8 Position estimation error obtained by the rotor position estimation method with Arctan function

图9 基于锁相环的位置估算方法得到的转子位置图Fig.9 Rotor position based on the position estimation method with the phase-locked loop

图10 基于锁相环的转子位置估算误差Fig.10 Rotor position estimation error based on phase-locked loop

仿真结果分析：由图7、图8可知，利用Arctan函数的转子位置估算方法在电机启动过程中、突加负载、电机突然给定反向速度时，估算误差较大，抗干扰性较差，且在稳定运行时，估算出的位置角度滞后，对于干扰较多且要求动态响应快的场合不适宜应用。由图9、图10可知，基于锁相环的位置估算方法在启动过程中、突加负载、电机突然给定反向速度时，估算误差角度接近0，抗干扰性强，且在稳定运行时，估算出的位置角度不滞后。

4.2 实验结果分析

4.1节已经对基于高频电压信号注入法的无位置传感器控制策略进行了理论分析与仿真研究，本节对所提出利用锁相环策略的转子位置估算方法进行了实验验证，控制芯片采用TI公司的TMS320F28035芯片，空调压缩机内的永磁同步电机参数为：P=800 W，极对数p=6，额定电压48 V，额定电流15 A，定子电阻0.232 Ω。PWM开关载频10 kHz，死区时间3µs。逆变器桥臂采用并联MOSFET的方式增大过流能力。采用id=0的策略，速度环和电流环都采用传统PI进行调节。实验平台如图11所示。

图11 压缩机低速无位置传感器控制实验平台Fig.11 Experimental platform of compressor with low speed position sensorless control

实验结果分析：实验设定转速为10 r/min，图12、图13分别为空载、负载5 N·m的运行工况实验波形图，由图12、图13可知，基于锁相环的位置估算方法得到的转子位置波形较平滑，估算出的位置波形基本可以与实际的位置波形重合。

图12 空载实验波形图Fig.12 The test waveforms with no-load

图13 5 N·m负载实验波形图Fig.13 The test waveforms with load of 5 N·m

5 结论

针对压缩机内置式永磁同步电机低速位置开环运行时响应慢、无法大功率启动、控制精度低等问题，通过分析内置式永磁同步电机在脉振高频正弦电压下的高频电流响应模型，提出了一种基于锁相环策略的转子位置估算方法，为了使电机可靠、稳定的启动，提出了一种利用d轴的高频响应电流进行积分的初始磁极方向识别方法，该方法对采样精度要求较低，算法执行时间短。为了验证提出的方法，搭建了仿真模型与实验平台，仿真与实验结果证明了所提出方法的有效性。