流化床内多组分颗粒传质过程模拟

2021-01-21宋晓皎杨学松殷维杰

动力工程学报 2021年1期

宋晓皎，王琦，杨学松，殷维杰

(1．山西能源学院能源与动力工程系，山西晋中 030600；2．哈尔滨工业大学能源科学与工程学院，哈尔滨 150001)

流化床反应器因其优良的传质和传热特性被广泛应用到各种工业化生产中[1-2]，而反应器中相间传质过程在一定程度上决定了反应特性的优良，因此流化床内传质特性成为国内外研究的热点问题[3-4]。Dong等[5-6]基于能量最小多尺度模型提出了多尺度传质模型，并用该模型模拟研究了臭氧的分解过程，结果显示在反应器中密相区域和稀相区域的臭氧分解存在明显不同。Saboni等[7]利用数值有限差分法研究了液体与单颗粒之间的传质系数变化规律，结果表明传质系数与雷诺数(Re)和施密特数(Sc)存在密切关系，并得出了单颗粒与液体之间的舍伍德数(Sh)表达式。Wang等[8]基于颗粒聚团介尺度模型，将质量传递与格子玻尔兹曼理论(LBM)相结合，研究了颗粒聚团对单组分颗粒与气体之间传质的影响，结果显示颗粒速度和体积分数都受到颗粒聚团的影响，并证实气固反应中舍伍德数与雷诺数成正向关系。

笔者基于Euler-Euler双流体模型，应用气泡介尺度理论，利用计算流体动力学(CFD)软件模拟了多组分颗粒在流化床反应器内的传质过程，比较分析了2种颗粒分别在混合和分离2种状态下与反应气体的传质特性，同时探究了入口表观气体速度、反应气体质量分数和床层压强等外部操作条件对传质过程的影响。

1 数学模型

基于Euler-Euler双流体模型，同时考虑气泡介尺度对多组分颗粒流化过程的影响，结合传质模型，在假定固相均为单一直径球形颗粒的基础上，利用CFD软件对水蒸气吸附过程进行数值模拟。

1.1 数学模型

Euler-Euler双流体模型基于连续性假设，固体颗粒和气体被认为拟流体和连续性介质来处理，并且它们所占据的空间位置是连续分布的。计算过程中涉及到的基本守恒方程如下。

质量守恒方程为：

(1)

(2)

动量守恒方程为：

(3)

(4)

式中：τ为压力张量；g为重力加速度；p为压力；β为曳力系数；为向量微分算子符号；下角标j为三维空间中另一个方向。

第m相颗粒的压力张量τmij及动力黏度μm为：

(5)

(6)

式中：η为颗粒弹性恢复系数；δ为固相与壁面间夹角的角系数；g0为径向分布函数，是用来描述固相间相对空间位置关系的统计函数；μ为动力黏度；μ*为特征动力黏度；α为动力黏度修正因子；下角标b为气泡相。

固相间摩擦应力的表征引用Srivastava等[13]提出的模型，其中摩擦应力pf、临界状态摩擦应力pcr和黏性系数μf为：

(7)

(8)

(9)

引用Syamlal[14]提出的固相间的动量传递系数ζmn，其表达式为：

(10)

式中：C为传统曳力模型有效曳力系数。

上式中g0,mn引用Lebowitz[15]提出的表达式：

(11)

组分守恒方程为：

(13)

式中：w为两相反应生成物的质量分数；D为两相反应物之间的组分扩散系数。

颗粒拟温度方程为：

(14)

式中：γ和Π为由于相间滑移而导致的能量碰撞耗散项及动能产生项；κ为由于颗粒运动碰撞而存在的热传导项。

1.2 气泡介尺度曳力模型

考虑到气泡介尺度对流化床内气固流动和传质的影响，在单组分颗粒气泡介尺度曳力模型[16]的基础上，构建多组分颗粒气泡介尺度曳力模型。基于气泡内无颗粒相存在的假设，得到多组分颗粒各固体相的曳力系数β1和β2：

(15)

(16)

式中：Uslip1和Uslip2分别为活性颗粒和惰性颗粒的表观滑移速度；dp1和dp2分别为活性颗粒和惰性颗粒的直径；φb为气泡体积分数；ab为气泡加速度；下角标es1、es2为乳化相中第1种颗粒和第2种颗粒。

基于此，为更好地表征考虑气泡介尺度后曳力模型的变化情况，引入非均质系数Hd：

Hd=βbubble-based/βWEN-YU

(17)

其中，

(18)

式中：CD为单个颗粒的曳力系数；βWEN-YU和βbubble-based分别为WEN-YU曳力系数和气泡介尺度曳力系数；des为乳化相颗粒的直径。

1.3 传质模型

假设整个传质过程为等温过程，气固之间传质由质量传递控制，固相颗粒对水蒸气的吸附速率表达式[13]为：

(19)

式中：mm为固相吸附水蒸气的质量；Sm为活性颗粒表面积；wm,pe和wm,ps分别为活性颗粒周围和颗粒表面的水蒸气质量分数，其中颗粒表面的水蒸气质量分数假设为0；kg为传质系数，与舍伍德数有关。

kg的表达式如下：

kg=Sh×Dg/dp1

(20)

式中：Dg为反应气体的扩散系数。

根据研究工况，选取la Nauze等[17]提出的舍伍德数公式作为经验公式，将其应用于本文传质部分后续研究，其表达式为：

Sh=2×φg+0.69×φg×[(Re/φg)a×Scb]

(21)

式中：a、b为经验系数，分别为0.5和0.333。

1.4 几何模型和计算参数

模拟计算中采用的流化床反应器结构如图1所示，用硅胶颗粒作为吸附剂，铜颗粒作为惰性颗粒，以探究惰性颗粒存在情况下活性颗粒的传质特性。模拟计算所采用的初始条件、边界条件以及相关的主要物性参数见表1。

图1 长方体反应器结构示意图

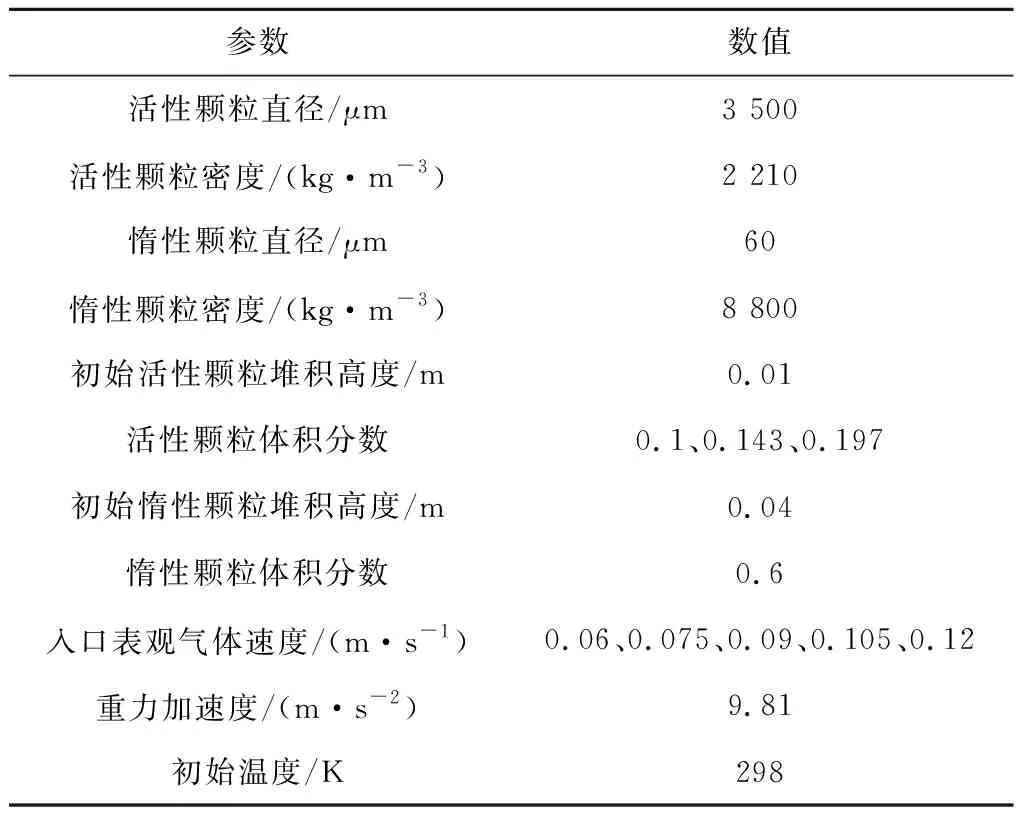
表1 模拟参数

1.5 网格独立性验证

网格独立性验证结果如图2所示，其中网格数分别为5 000、10 000和15 000，入口表观气体速度Ug=0.12 m/s，初始时刻床层内部堆积活性颗粒的质量分数wactive0=1.5%。从图2可以明显观察到，随着网格尺寸的减小，预测结果差别逐渐减小，当网格数为15 000和10 000时，预测结果几乎没有差别。因此，根据模拟结果精确度和计算耗时，采用10 000个网格数作为后期模拟采用的网格数。

图2 不同网格数计算时舍伍德数模拟结果对比

2 结果与分析

为了对Gidaspow和气泡介尺度2种曳力模型进行比较分析，图3给出了采用不同曳力模型时模拟获得的活性颗粒对水蒸气的吸附速率。模拟中Ug=0.12 m/s，wactive0选取1.0%、1.5%和2.0%。从图3可以明显观察到，无论应用哪一种曳力模型，活性颗粒对水蒸气的吸附速率都随着活性颗粒质量分数的增大而增大。相比于Gidaspow曳力模型模拟结果，气泡介尺度曳力模型模拟获得的活性颗粒对水蒸气的吸附速率均较小。这主要是由于气泡介尺度曳力模型充分考虑流化床内气固非均质特性，当气体以气泡形式穿过床层内部时，导致颗粒聚集形成颗粒聚团，使得活性颗粒与水蒸气接触面积减小，降低了对水蒸气的吸附效果，所以对水蒸气的吸附速率较小。

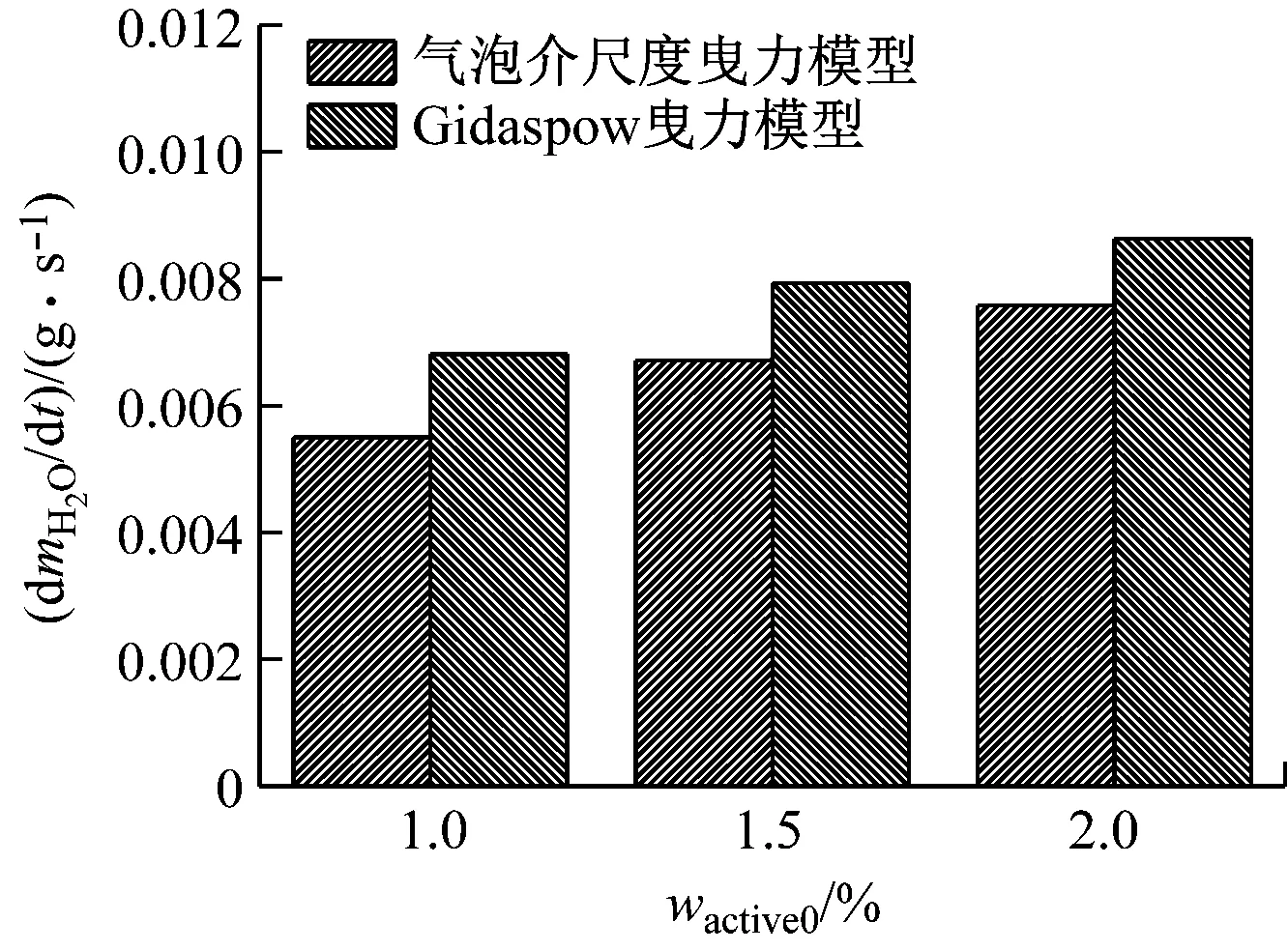
图3 活性颗粒对水蒸气的吸附速率

基于2种曳力模型的对比分析，为了验证气泡介尺度曳力模型和传质模型，图4给出了入口表观气体速度和水蒸气质量分数给定情况下舍伍德数模拟结果与Qin等[12]的实验结果的比较。由图4可知，气泡介尺度曳力模型模拟得到的舍伍德数与实验结果更贴近，最大相对误差不超过5%；而Gidaspow曳力模型模拟得到的舍伍德数与实验结果差距较大，相对误差远远超过了5%；因此，气泡介尺度曳力模型的，误差在可接受范围内,其模拟结果更合理。

不同入口表观气体速度条件下，惰性颗粒非均质系数Hd随床层空隙率的变化情况如图5所示。由图5可知，随着活性颗粒体积分数的增大，惰性颗粒的非均质系数Hd逐渐减小，这一现象说明气泡对床内颗粒流动及传质具有较大的影响，床层内部气固非均质现象不可忽略，同时还可以观察到，在活性颗粒体积分数和入口表观气体速度较大时，惰性颗粒非均质系数更小，即气泡介尺度的存在对床层非均质性影响程度更深。因此，气泡介尺度曳力模型能更好地模拟再现活性颗粒对水蒸气的吸附过程，说明了相比于传统曳力模型而言，气泡介尺度曳力模型的准确性有所提升。

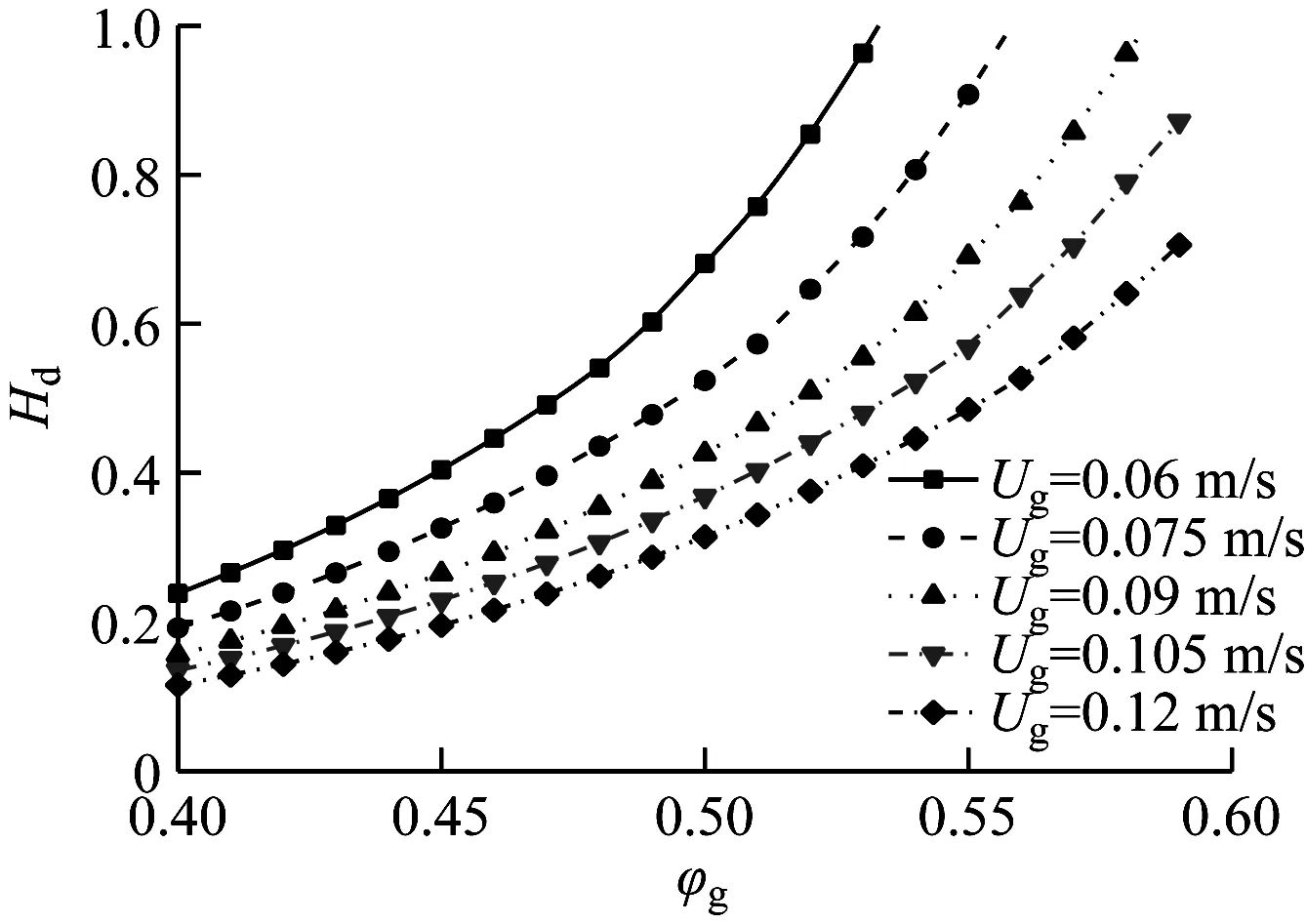
图5 非均质系数随床层空隙率的变化

图6给出了2种颗粒在t=10 s时不同入口表观气体速度条件下颗粒体积分数的分布情况。由图6可知，惰性颗粒床层高度随着入口表观气体速度的增大而逐渐膨胀增加，床层上部的活性颗粒轴向高度也逐渐变大，整个床层内部的气泡相越发明显，体积分数逐渐增大，同时活性颗粒与惰性颗粒的混合程度逐渐加深。这主要是由于入口表观气体速度增大使得床层内部聚集形成更多气泡，气泡穿过床层时扰动床层颗粒相，从而增加颗粒混合程度，产生更明显的颗粒聚团现象。

(a) 惰性颗粒

不同入口表观气体速度条件下，t=10 s时床层内部水蒸气质量分数的分布情况如图7所示。由图7可知，入口表观气体速度通过影响气泡运动间接对水蒸气吸附过程产生影响。从图7可以明显观察到，入口表观气体速度越大，随着床层高度的增加，水蒸气质量分数减幅逐渐变缓，致使反应器出口处水蒸气质量分数逐渐增大。这是由于入口表观气体速度增大，床层内部有更多气泡穿过，使得颗粒聚团现象加深，水蒸气与活性颗粒有效接触面积减小，活性颗粒对水蒸气的吸附效果减弱。

图7 不同入口表观气体速度时水蒸气质量分数分布云图

活性颗粒质量分数为1.5%时，水蒸气吸附速率和舍伍德数随入口表观气体速度的变化情况如图8所示。由图8可知，随着入口表观气体速度的增大，水蒸气吸附速率和舍伍德数逐渐减小，活性颗粒对水蒸气的吸附效果减弱。这是由于较高的入口表观气体速度使得更多的水蒸气以气泡形式穿过床层，削弱了水蒸气与活性颗粒的接触反应。并且相比于图4中活性颗粒质量分数对舍伍德数的影响，入口表观气体速度对水蒸气吸附效果的影响程度更加显著，从另一方面说明，减小入口表观气体速度可以更有效地促进气固间的传质过程。

(a) 水蒸气吸附速率

活性颗粒质量分数为1.5%，入口表观气体速度为0.12 m/s时，水蒸气吸附速率和舍伍德数随入口水蒸气质量分数的变化情况如图9所示。由图9可知，当入口水蒸气质量分数为0.007～0.14时，随着入口水蒸气质量分数的增大，水蒸气吸附速率和舍伍德数逐渐增大，活性颗粒对水蒸气的吸附效果增强，并且当入口水蒸气质量分数较低时，舍伍德数增幅较缓。并且相比于图8中入口表观气体速度对舍伍德数的影响，增大入口水蒸气质量分数对吸附效果的影响更明显，说明适当地增大入口水蒸气质量分数可以更有效地改善传质过程。

(a) 水蒸气吸附速率

除入口表观气体速度和水蒸气质量分数等因素外，床层内部压强也会通过影响床层中气泡特性来间接影响水蒸气的吸附反应。图10给出了不同床层压强下活性颗粒对水蒸气吸附过程的传质系数、吸附速率和舍伍德数的变化情况。从图10可以明显观察到，床层压强升高有利于水蒸气吸附过程的进行。Song等[18]通过实验研究了床层压强对气泡特性的影响，指出床层压强升高会减小气泡尺寸。因此，随着床层压强的变化，气泡尺寸发生变化，对气固相间的传质特性产生直接影响。随着床层压强的降低，形成的气泡体积逐渐增大，气泡通过床层内部时导致更多的水蒸气在不参与反应的情况下就穿过床层，从而使得传质系数、吸附速率和舍伍德数都减小。当床层压强较高时，传质系数、吸附速率和舍伍德数的变化速率越来越小。这说明床层压强较高时，通过改变床层压强来改善传质过程效果不佳。而相比于入口表观气体速度和入口水蒸气质量分数对舍伍德数的影响，增大床层压强对吸附效果的影响较弱，进一步说明通过改变床层压强来改善传质过程效果甚微。